河北省保定市高阳中学2013-2014学年高一下学期第十九次周练数学试题
文档属性
| 名称 | 河北省保定市高阳中学2013-2014学年高一下学期第十九次周练数学试题 |

|
|
| 格式 | zip | ||
| 文件大小 | 126.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-07-09 00:00:00 | ||
图片预览

文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
高阳中学2013-2014学年高一下学期第十九次周练
数学试题
一、选择题
1.若直线a和b没有公共点,则a与b的位置关系是( )
A.相交 B.平行
C.异面 D.平行或异面
2.平行六面体ABCD-A1B1C1D1中,既与AB共面也与CC1共面的棱的条数为( )
A.3 B.4 C.5 D.6
3.已知平面α和直线l,则α内至少有一条直线与l( )
A.平行 B.相交 C.垂直 D.异面
4.长方体ABCD-A1B1C1D1中,异面直线AB,A1D1所成的角等于( )
A.30° B.45° C.60° D.90°
5.对两条不相交的空间直线a与b,必存在平面α,使得( )
A. a α,b α B.a α,b∥α
C.a⊥α,b⊥α D.a α,b⊥α
6.下面四个命题:
①若直线a,b异面,b,c异面,则a,c异面;
②若直线a,b相交,b,c相交,则a,c相交;
③若a∥b,则a,b与c所成的角相等;
④若a⊥b,b⊥c,则a∥c.
其中真命题的个数为( )
A.4 B.3 C.2 D.1
7.在正方体ABCD-A1B1C1D1中,E,F分别是线段A1B1,B1C1上的不与端点重合的动点,如果A1E=B1F,有下面四个结论:21世纪教育网版权所有
①EF⊥AA1;②EF∥AC;③EF与AC异面;④EF∥平面ABCD.
其中一定正确的有( )
A.①② B.②③ C.②④ D.①④
8.设a,b为两条不重合的直线,α,β为两个不重合的平面,下列命题中为真命题的是( )
A.若a,b与α所成的角相等,则a∥b
B.若a∥α,b∥β,α∥β,则a∥b
C.若a α,b β,a∥b,则α∥β
D.若a⊥α,b⊥β,α⊥β,则a⊥b
9.已知平面α⊥平面β,α∩β=l,点A ( http: / / www.21cnjy.com )∈α,A l,直线AB∥l,直线AC⊥l,直线m∥α,n∥β,则下列四种位置关系中,不一定成立的是( )21cnjy.com
A.AB∥m B.AC⊥m
C.AB∥β D.AC⊥β
10.(2012·大纲版数学(文科))已知 ( http: / / www.21cnjy.com )正方体ABCD-A1B1C1D1中,E、F分别为BB1、CC1的中点,那么直线AE与D1F所成角的余弦值为( )21·cn·jy·com
A.- B. .
C. D.-
11.已知三棱锥D-ABC的三个侧面与底面 ( http: / / www.21cnjy.com )全等,且AB=AC=,BC=2,则以BC为棱,以面BCD与面BCA为面的二面角的余弦值为( )21教育网
A. B. C.0 D.-
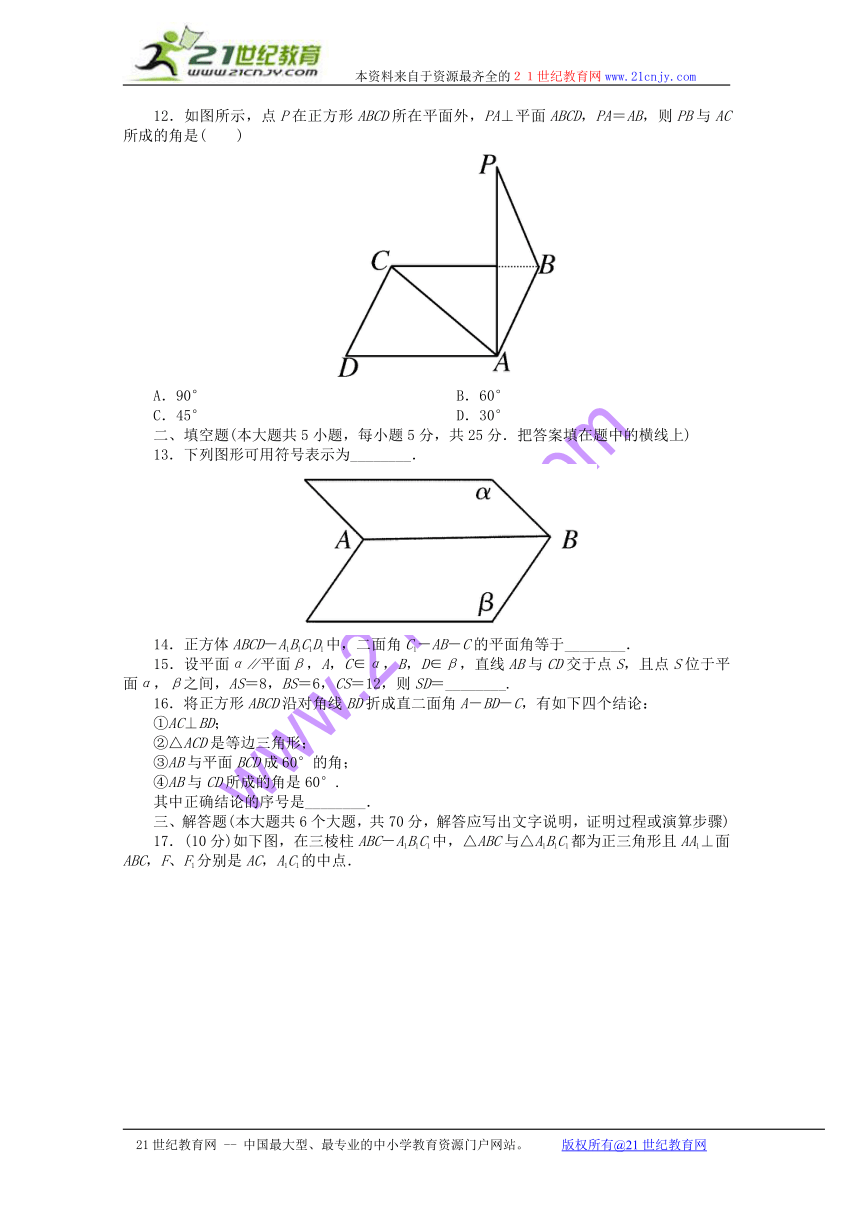
12.如图所示,点P在正方形ABCD所在平面外,PA⊥平面ABCD,PA=AB,则PB与AC所成的角是( )www.21-cn-jy.com
A.90° B.60°
C.45° D.30°
二、填空题(本大题共5小题,每小题5分,共25分.把答案填在题中的横线上)
13.下列图形可用符号表示为________.
14.正方体ABCD-A1B1C1D1中,二面角C1-AB-C的平面角等于________.
15.设平面α∥平面β,A ( http: / / www.21cnjy.com ),C∈α,B,D∈β,直线AB与CD交于点S,且点S位于平面α,β之间,AS=8,BS=6,CS=12,则SD=________.21·世纪*教育网
16.将正方形ABCD沿对角线BD折成直二面角A-BD-C,有如下四个结论:
①AC⊥BD;
②△ACD是等边三角形;
③AB与平面BCD成60°的角;
④AB与CD所成的角是60°.
其中正确结论的序号是________.
三、解答题(本大题共6个大题,共70分,解答应写出文字说明,证明过程或演算步骤)
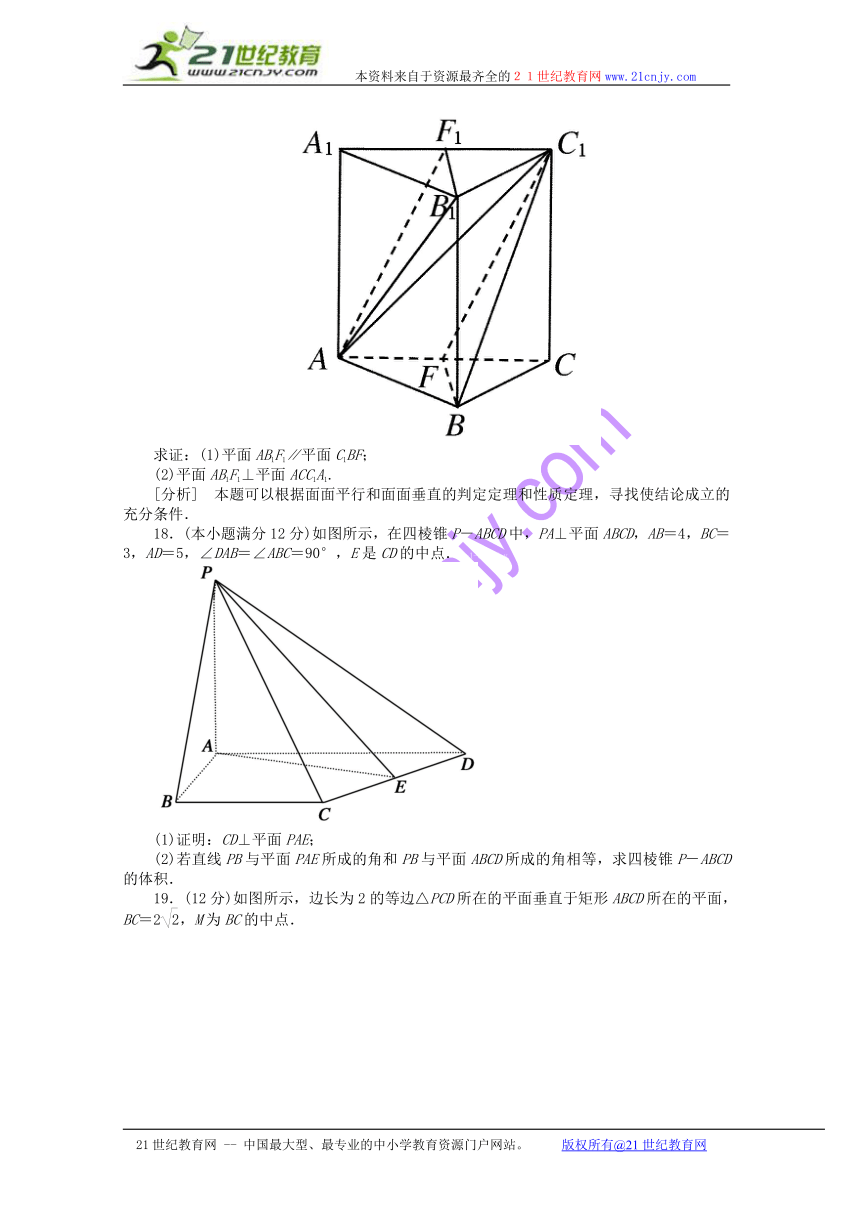
17.(10分)如下图,在三棱柱ABC ( http: / / www.21cnjy.com )-A1B1C1中,△ABC与△A1B1C1都为正三角形且AA1⊥面ABC,F、F1分别是AC,A1C1的中点.www-2-1-cnjy-com
求证:(1)平面AB1F1∥平面C1BF;
(2)平面AB1F1⊥平面ACC1A1.
[分析] 本题可以根据面面平行和面面垂直的判定定理和性质定理,寻找使结论成立的充分条件.
18.(本小题满分12分)如图所示 ( http: / / www.21cnjy.com ),在四棱锥P-ABCD中,PA⊥平面ABCD,AB=4,BC=3,AD=5,∠DAB=∠ABC=90°,E是CD的中点.2-1-c-n-j-y
(1)证明:CD⊥平面PAE;
(2)若直线PB与平面PAE所成的角和PB与平面ABCD所成的角相等,求四棱锥P-ABCD的体积.
19.(12分)如图所示,边长为2的等边△PCD所在的平面垂直于矩形ABCD所在的平面,BC=2,M为BC的中点. 21*cnjy*com
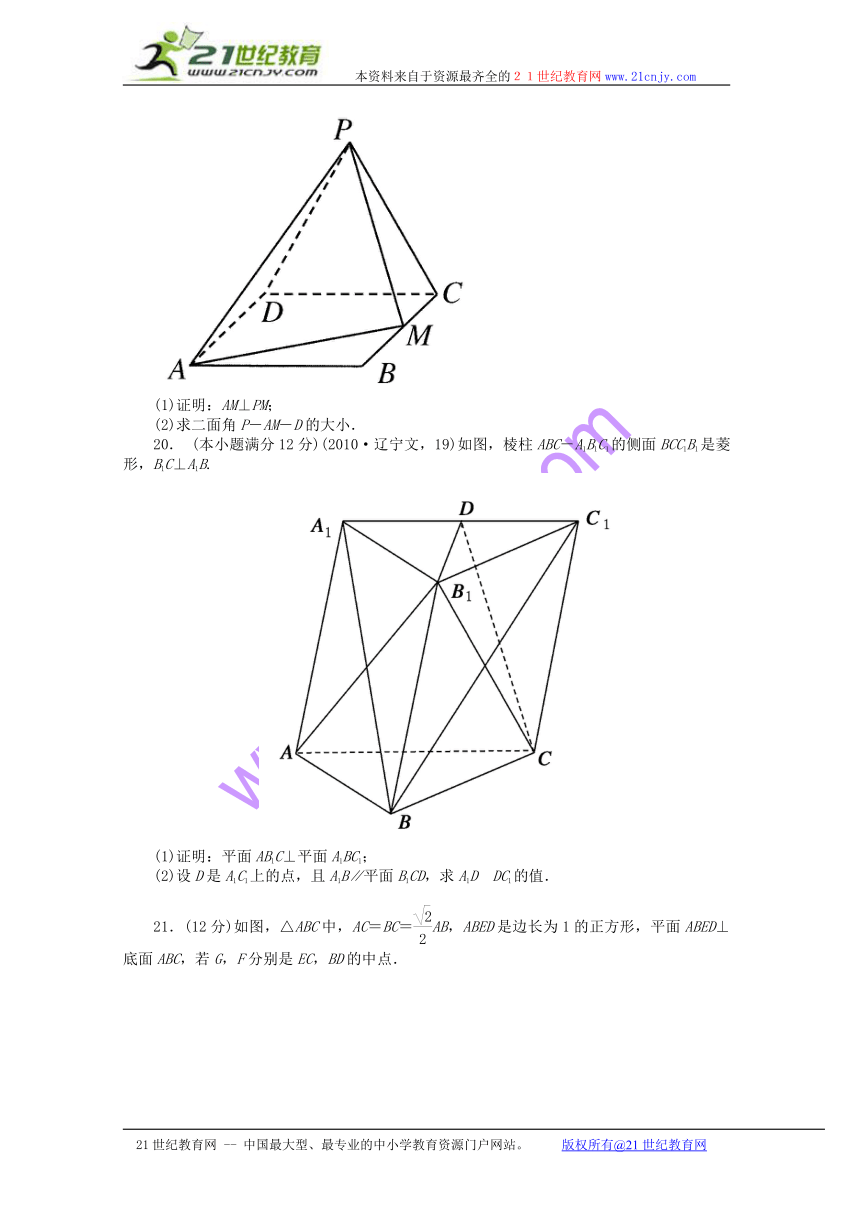
(1)证明:AM⊥PM;
(2)求二面角P-AM-D的大小.
20. (本小题满分12分)(2010·辽宁文,19)如图,棱柱ABC-A1B1C1的侧面BCC1B1是菱形,B1C⊥A1B.【来源:21cnj*y.co*m】
(1)证明:平面AB1C⊥平面A1BC1;
(2)设D是A1C1上的点,且A1B∥平面B1CD,求A1D?DC1的值.
21.(12分)如图,△ABC中, ( http: / / www.21cnjy.com )AC=BC=AB,ABED是边长为1的正方形,平面ABED⊥底面ABC,若G,F分别是EC,BD的中点.【出处:21教育名师】
(1)求证:GF∥底面ABC;
(2)求证:AC⊥平面EBC;
(3)求几何体ADEBC的体积V.
[分析] (1)转化为证明GF平行于平面AB ( http: / / www.21cnjy.com )C内的直线AC;(2)转化为证明AC垂直于平面EBC内的两条相交直线BC和BE;(3)几何体ADEBC是四棱锥C-ABED.
22.(12分)如下图所示,在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5,AA1=4,点D是AB的中点.【版权所有:21教育】
(1)求证:AC⊥BC1;
(2)求证:AC1∥平面CDB1;
(3)求异面直线AC1与B1C所成角的余弦值.
答案
1[答案] D
2[答案] C
3[答案] C
4[答案] D
5[答案] B
6[答案] D
7[答案] D
8[答案] D
9[答案] C
10[答案]
11[答案] C
12[答案] B
13[答案] α∩β=AB
14[答案] 45°
15[答案] 9
16[答案] ①②④
17[证明] (1)在正三棱柱ABC-A1B1C1中,
∵F、F1分别是AC、A1C1的中点,
∴B1F1∥BF,AF1∥C1F.
又∵B1F1∩AF1=F1,C1F∩BF=F,
∴平面AB1F1∥平面C1BF.
(2)在三棱柱ABC-A1B1C1中,AA1⊥平面A1B1C1,∴B1F1⊥AA1.
又B1F1⊥A1C1,A1C1∩AA1=A1,
∴B1F1⊥平面ACC1A1,而B1F1 平面AB1F1,
∴平面AB1F1⊥平面ACC1A1.
18
(1)如图所示,连接AC,由AB=4,BC=3,∠ABC=90°,得AC=5.
又AD=5,E是CD的中点,所以CD⊥AE.
∵PA⊥平面ABCD,CD 平面ABCD,所以PA⊥CD.
而PA,AE是平面PAE内的两条相交直线,所以CD⊥平面PAE.
(2)过点B作BG∥CD,分别与AE,AD相交于F,G,连接PF.
由(1)CD⊥平面PAE知,BG⊥平面PAE.于是∠BPF为直线PB与平面PAE所成的角,且BG⊥AE.2·1·c·n·j·y
由PA⊥平面ABCD知,∠PBA为直线PB与平面ABCD所成的角.
AB=4,AG=2,BG⊥AF,由题意,知∠PBA=∠BPF,
因为sin∠PBA=,sin∠BPF=,所以PA=BF.
由∠DAB=∠ABC=90°知,AD∥BC,又BG∥CD,所以四边形BCDG是平行四边形,故GD=BC=3.于是AG=2.【来源:21·世纪·教育·网】
在Rt△BAG中,AB=4,AG=2,BG⊥AF,所以
BG==2,BF===.于是PA=BF=.
又梯形ABCD的面积为S=×(5+3)×4=16,所以四棱锥P-ABCD的体积为
V=×S×PA=×16×=.
19 (1)证明:如图所示,取CD的中点E,连接PE,EM,EA,
∵△PCD为正三角形,
∴PE⊥CD,PE=PDsin∠PDE=2sin60°=.
∵平面PCD⊥平面ABCD,
∴PE⊥平面ABCD,而AM 平面ABCD,∴PE⊥AM.
∵四边形ABCD是矩形,
∴△ADE,△ECM,△ABM均为直角三角形,由勾股定理可求得EM=,AM=,AE=3,
∴EM2+AM2=AE2.∴AM⊥EM.
又PE∩EM=E,∴AM⊥平面PEM,∴AM⊥PM.
(2)解:由(1)可知EM⊥AM,PM⊥AM,
∴∠PME是二面角P-AM-D的平面角.
∴tan∠PME===1,∴∠PME=45°.
∴二面角P-AM-D的大小为45°.
20
(1)因为侧面BCC1B1是菱形,所以B1C⊥BC1,
又已知B1C⊥A1B,且A1B∩BC1=B,
所以B1C⊥平面A1BC1,又B1C 平面AB1C
所以平面AB1C⊥平面A1BC1 .
(2)设BC1交B1C于点E,连接DE,则DE是平面A1BC1与平面
B1CD的交线.
因为A1B∥平面B1CD,A1B 平面A1BC1,平面A1BC1∩平面B1CD=DE,所以A1B∥DE.
又E是BC1的中点,所以D为A1C1的中点.
即A1D?DC1=1.
21[解] (1)证明:连接AE,如下图所示.
∵ADEB为正方形,
∴AE∩BD=F,且F是AE的中点,
又G是EC的中点,
∴GF∥AC,又AC 平面ABC,GF 平面ABC,
∴GF∥平面ABC.
(2)证明:∵ADEB为正方形,∴EB⊥AB,
又∵平面ABED⊥平面ABC,平面ABED∩平面ABC=AB,EB 平面ABED,
∴BE⊥平面ABC,∴BE⊥AC.
又∵AC=BC=AB,
∴CA2+CB2=AB2,
∴AC⊥BC.
又∵BC∩BE=B,∴AC⊥平面BCE.
(3)取AB的中点H,连GH,∵BC=AC=AB=,
∴CH⊥AB,且CH=,又平面ABED⊥平面ABC
∴GH⊥平面ABCD,∴V=×1×=.
22 (1)证明:在直三棱柱ABC-A1B1C1中,底面三边长AC=3,BC=4,AB=5,∴AC⊥BC.
又∵C1C⊥AC.∴AC⊥平面BCC1B1.
∵BC1 平面BCC1B,∴AC⊥BC1.
(2)证明:设CB1与C1B的交点为E,连接DE,又四边形BCC1B1为正方形.
∵D是AB的中点,E是BC1的中点,∴DE∥AC1.
∵DE 平面CDB1,AC1 平面CDB1,
∴AC1∥平面CDB1.
(3)解:∵DE∥AC1,
∴∠CED为AC1与B1C所成的角.
在△CED中,ED=AC1=,
CD=AB=,CE=CB1=2,
∴cos∠CED==.
∴异面直线AC1与B1C所成角的余弦值为.
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
高阳中学2013-2014学年高一下学期第十九次周练
数学试题
一、选择题
1.若直线a和b没有公共点,则a与b的位置关系是( )
A.相交 B.平行
C.异面 D.平行或异面
2.平行六面体ABCD-A1B1C1D1中,既与AB共面也与CC1共面的棱的条数为( )
A.3 B.4 C.5 D.6
3.已知平面α和直线l,则α内至少有一条直线与l( )
A.平行 B.相交 C.垂直 D.异面
4.长方体ABCD-A1B1C1D1中,异面直线AB,A1D1所成的角等于( )
A.30° B.45° C.60° D.90°
5.对两条不相交的空间直线a与b,必存在平面α,使得( )
A. a α,b α B.a α,b∥α
C.a⊥α,b⊥α D.a α,b⊥α
6.下面四个命题:
①若直线a,b异面,b,c异面,则a,c异面;
②若直线a,b相交,b,c相交,则a,c相交;
③若a∥b,则a,b与c所成的角相等;
④若a⊥b,b⊥c,则a∥c.
其中真命题的个数为( )
A.4 B.3 C.2 D.1
7.在正方体ABCD-A1B1C1D1中,E,F分别是线段A1B1,B1C1上的不与端点重合的动点,如果A1E=B1F,有下面四个结论:21世纪教育网版权所有
①EF⊥AA1;②EF∥AC;③EF与AC异面;④EF∥平面ABCD.
其中一定正确的有( )
A.①② B.②③ C.②④ D.①④
8.设a,b为两条不重合的直线,α,β为两个不重合的平面,下列命题中为真命题的是( )
A.若a,b与α所成的角相等,则a∥b
B.若a∥α,b∥β,α∥β,则a∥b
C.若a α,b β,a∥b,则α∥β
D.若a⊥α,b⊥β,α⊥β,则a⊥b
9.已知平面α⊥平面β,α∩β=l,点A ( http: / / www.21cnjy.com )∈α,A l,直线AB∥l,直线AC⊥l,直线m∥α,n∥β,则下列四种位置关系中,不一定成立的是( )21cnjy.com
A.AB∥m B.AC⊥m
C.AB∥β D.AC⊥β
10.(2012·大纲版数学(文科))已知 ( http: / / www.21cnjy.com )正方体ABCD-A1B1C1D1中,E、F分别为BB1、CC1的中点,那么直线AE与D1F所成角的余弦值为( )21·cn·jy·com
A.- B. .
C. D.-
11.已知三棱锥D-ABC的三个侧面与底面 ( http: / / www.21cnjy.com )全等,且AB=AC=,BC=2,则以BC为棱,以面BCD与面BCA为面的二面角的余弦值为( )21教育网
A. B. C.0 D.-
12.如图所示,点P在正方形ABCD所在平面外,PA⊥平面ABCD,PA=AB,则PB与AC所成的角是( )www.21-cn-jy.com
A.90° B.60°
C.45° D.30°
二、填空题(本大题共5小题,每小题5分,共25分.把答案填在题中的横线上)
13.下列图形可用符号表示为________.
14.正方体ABCD-A1B1C1D1中,二面角C1-AB-C的平面角等于________.
15.设平面α∥平面β,A ( http: / / www.21cnjy.com ),C∈α,B,D∈β,直线AB与CD交于点S,且点S位于平面α,β之间,AS=8,BS=6,CS=12,则SD=________.21·世纪*教育网
16.将正方形ABCD沿对角线BD折成直二面角A-BD-C,有如下四个结论:
①AC⊥BD;
②△ACD是等边三角形;
③AB与平面BCD成60°的角;
④AB与CD所成的角是60°.
其中正确结论的序号是________.
三、解答题(本大题共6个大题,共70分,解答应写出文字说明,证明过程或演算步骤)
17.(10分)如下图,在三棱柱ABC ( http: / / www.21cnjy.com )-A1B1C1中,△ABC与△A1B1C1都为正三角形且AA1⊥面ABC,F、F1分别是AC,A1C1的中点.www-2-1-cnjy-com
求证:(1)平面AB1F1∥平面C1BF;
(2)平面AB1F1⊥平面ACC1A1.
[分析] 本题可以根据面面平行和面面垂直的判定定理和性质定理,寻找使结论成立的充分条件.
18.(本小题满分12分)如图所示 ( http: / / www.21cnjy.com ),在四棱锥P-ABCD中,PA⊥平面ABCD,AB=4,BC=3,AD=5,∠DAB=∠ABC=90°,E是CD的中点.2-1-c-n-j-y
(1)证明:CD⊥平面PAE;
(2)若直线PB与平面PAE所成的角和PB与平面ABCD所成的角相等,求四棱锥P-ABCD的体积.
19.(12分)如图所示,边长为2的等边△PCD所在的平面垂直于矩形ABCD所在的平面,BC=2,M为BC的中点. 21*cnjy*com
(1)证明:AM⊥PM;
(2)求二面角P-AM-D的大小.
20. (本小题满分12分)(2010·辽宁文,19)如图,棱柱ABC-A1B1C1的侧面BCC1B1是菱形,B1C⊥A1B.【来源:21cnj*y.co*m】
(1)证明:平面AB1C⊥平面A1BC1;
(2)设D是A1C1上的点,且A1B∥平面B1CD,求A1D?DC1的值.
21.(12分)如图,△ABC中, ( http: / / www.21cnjy.com )AC=BC=AB,ABED是边长为1的正方形,平面ABED⊥底面ABC,若G,F分别是EC,BD的中点.【出处:21教育名师】
(1)求证:GF∥底面ABC;
(2)求证:AC⊥平面EBC;
(3)求几何体ADEBC的体积V.
[分析] (1)转化为证明GF平行于平面AB ( http: / / www.21cnjy.com )C内的直线AC;(2)转化为证明AC垂直于平面EBC内的两条相交直线BC和BE;(3)几何体ADEBC是四棱锥C-ABED.
22.(12分)如下图所示,在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5,AA1=4,点D是AB的中点.【版权所有:21教育】
(1)求证:AC⊥BC1;
(2)求证:AC1∥平面CDB1;
(3)求异面直线AC1与B1C所成角的余弦值.
答案
1[答案] D
2[答案] C
3[答案] C
4[答案] D
5[答案] B
6[答案] D
7[答案] D
8[答案] D
9[答案] C
10[答案]
11[答案] C
12[答案] B
13[答案] α∩β=AB
14[答案] 45°
15[答案] 9
16[答案] ①②④
17[证明] (1)在正三棱柱ABC-A1B1C1中,
∵F、F1分别是AC、A1C1的中点,
∴B1F1∥BF,AF1∥C1F.
又∵B1F1∩AF1=F1,C1F∩BF=F,
∴平面AB1F1∥平面C1BF.
(2)在三棱柱ABC-A1B1C1中,AA1⊥平面A1B1C1,∴B1F1⊥AA1.
又B1F1⊥A1C1,A1C1∩AA1=A1,
∴B1F1⊥平面ACC1A1,而B1F1 平面AB1F1,
∴平面AB1F1⊥平面ACC1A1.
18
(1)如图所示,连接AC,由AB=4,BC=3,∠ABC=90°,得AC=5.
又AD=5,E是CD的中点,所以CD⊥AE.
∵PA⊥平面ABCD,CD 平面ABCD,所以PA⊥CD.
而PA,AE是平面PAE内的两条相交直线,所以CD⊥平面PAE.
(2)过点B作BG∥CD,分别与AE,AD相交于F,G,连接PF.
由(1)CD⊥平面PAE知,BG⊥平面PAE.于是∠BPF为直线PB与平面PAE所成的角,且BG⊥AE.2·1·c·n·j·y
由PA⊥平面ABCD知,∠PBA为直线PB与平面ABCD所成的角.
AB=4,AG=2,BG⊥AF,由题意,知∠PBA=∠BPF,
因为sin∠PBA=,sin∠BPF=,所以PA=BF.
由∠DAB=∠ABC=90°知,AD∥BC,又BG∥CD,所以四边形BCDG是平行四边形,故GD=BC=3.于是AG=2.【来源:21·世纪·教育·网】
在Rt△BAG中,AB=4,AG=2,BG⊥AF,所以
BG==2,BF===.于是PA=BF=.
又梯形ABCD的面积为S=×(5+3)×4=16,所以四棱锥P-ABCD的体积为
V=×S×PA=×16×=.
19 (1)证明:如图所示,取CD的中点E,连接PE,EM,EA,
∵△PCD为正三角形,
∴PE⊥CD,PE=PDsin∠PDE=2sin60°=.
∵平面PCD⊥平面ABCD,
∴PE⊥平面ABCD,而AM 平面ABCD,∴PE⊥AM.
∵四边形ABCD是矩形,
∴△ADE,△ECM,△ABM均为直角三角形,由勾股定理可求得EM=,AM=,AE=3,
∴EM2+AM2=AE2.∴AM⊥EM.
又PE∩EM=E,∴AM⊥平面PEM,∴AM⊥PM.
(2)解:由(1)可知EM⊥AM,PM⊥AM,
∴∠PME是二面角P-AM-D的平面角.
∴tan∠PME===1,∴∠PME=45°.
∴二面角P-AM-D的大小为45°.
20
(1)因为侧面BCC1B1是菱形,所以B1C⊥BC1,
又已知B1C⊥A1B,且A1B∩BC1=B,
所以B1C⊥平面A1BC1,又B1C 平面AB1C
所以平面AB1C⊥平面A1BC1 .
(2)设BC1交B1C于点E,连接DE,则DE是平面A1BC1与平面
B1CD的交线.
因为A1B∥平面B1CD,A1B 平面A1BC1,平面A1BC1∩平面B1CD=DE,所以A1B∥DE.
又E是BC1的中点,所以D为A1C1的中点.
即A1D?DC1=1.
21[解] (1)证明:连接AE,如下图所示.
∵ADEB为正方形,
∴AE∩BD=F,且F是AE的中点,
又G是EC的中点,
∴GF∥AC,又AC 平面ABC,GF 平面ABC,
∴GF∥平面ABC.
(2)证明:∵ADEB为正方形,∴EB⊥AB,
又∵平面ABED⊥平面ABC,平面ABED∩平面ABC=AB,EB 平面ABED,
∴BE⊥平面ABC,∴BE⊥AC.
又∵AC=BC=AB,
∴CA2+CB2=AB2,
∴AC⊥BC.
又∵BC∩BE=B,∴AC⊥平面BCE.
(3)取AB的中点H,连GH,∵BC=AC=AB=,
∴CH⊥AB,且CH=,又平面ABED⊥平面ABC
∴GH⊥平面ABCD,∴V=×1×=.
22 (1)证明:在直三棱柱ABC-A1B1C1中,底面三边长AC=3,BC=4,AB=5,∴AC⊥BC.
又∵C1C⊥AC.∴AC⊥平面BCC1B1.
∵BC1 平面BCC1B,∴AC⊥BC1.
(2)证明:设CB1与C1B的交点为E,连接DE,又四边形BCC1B1为正方形.
∵D是AB的中点,E是BC1的中点,∴DE∥AC1.
∵DE 平面CDB1,AC1 平面CDB1,
∴AC1∥平面CDB1.
(3)解:∵DE∥AC1,
∴∠CED为AC1与B1C所成的角.
在△CED中,ED=AC1=,
CD=AB=,CE=CB1=2,
∴cos∠CED==.
∴异面直线AC1与B1C所成角的余弦值为.
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
同课章节目录
