幂函数的图像和性质[上学期]
文档属性
| 名称 | 幂函数的图像和性质[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 1005.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-08-20 17:08:00 | ||
图片预览





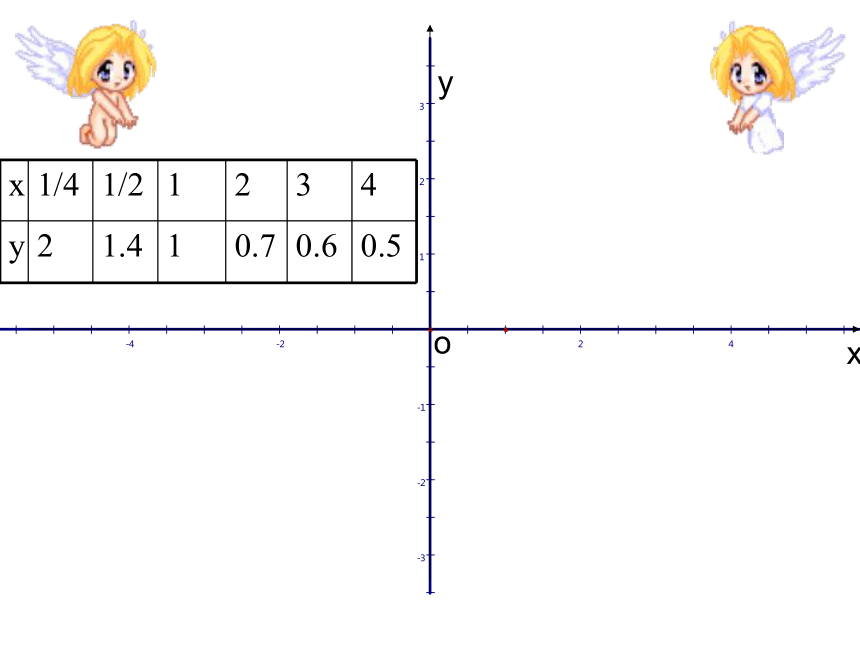
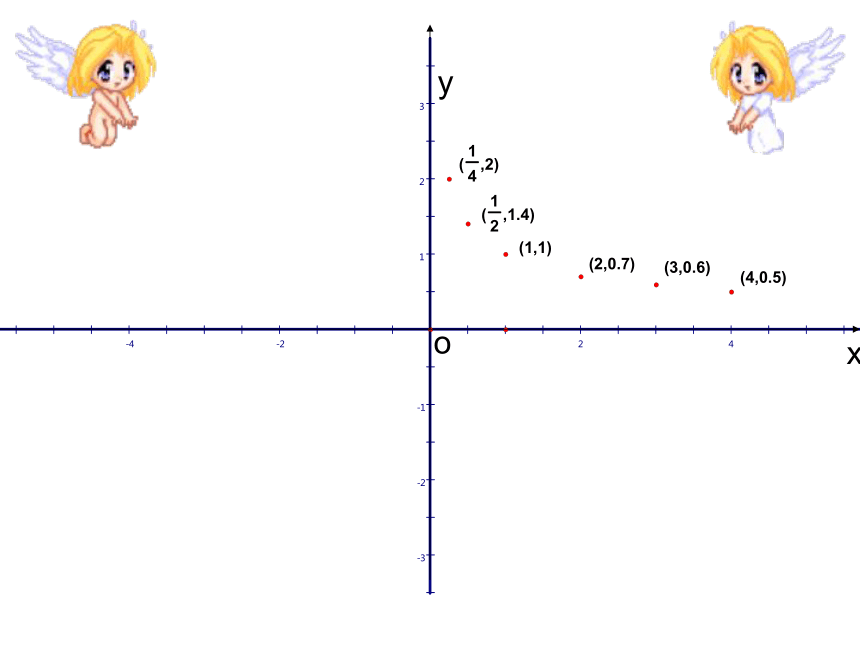
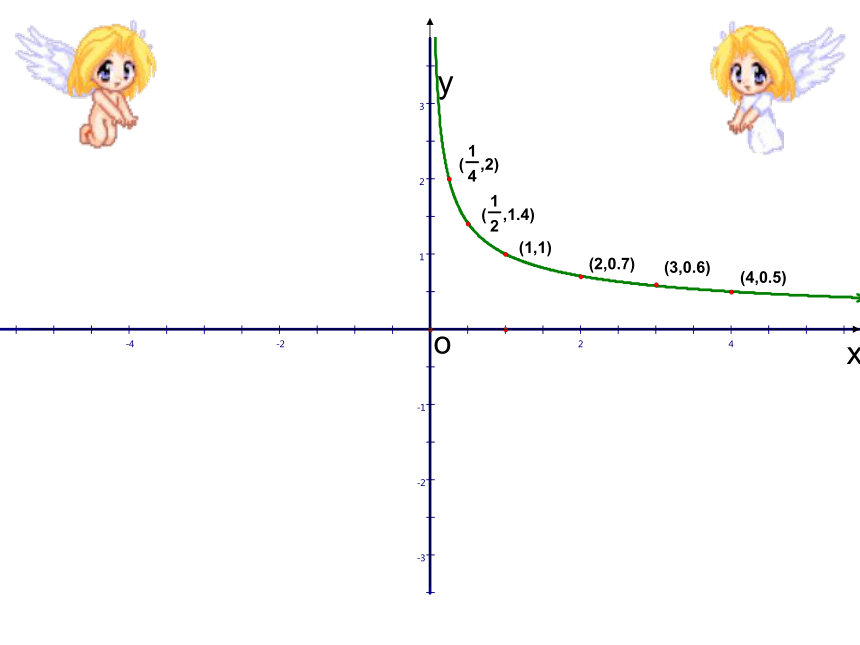

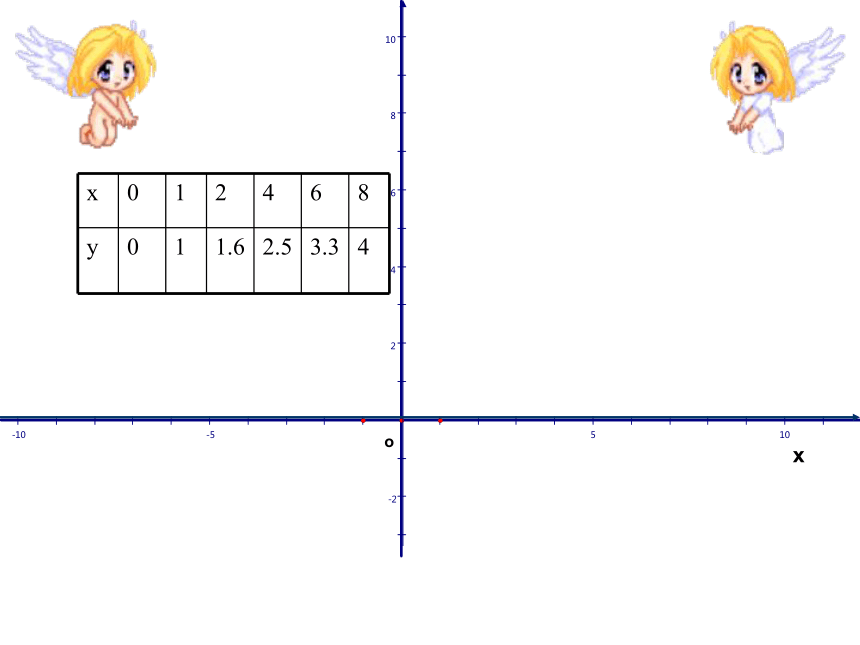
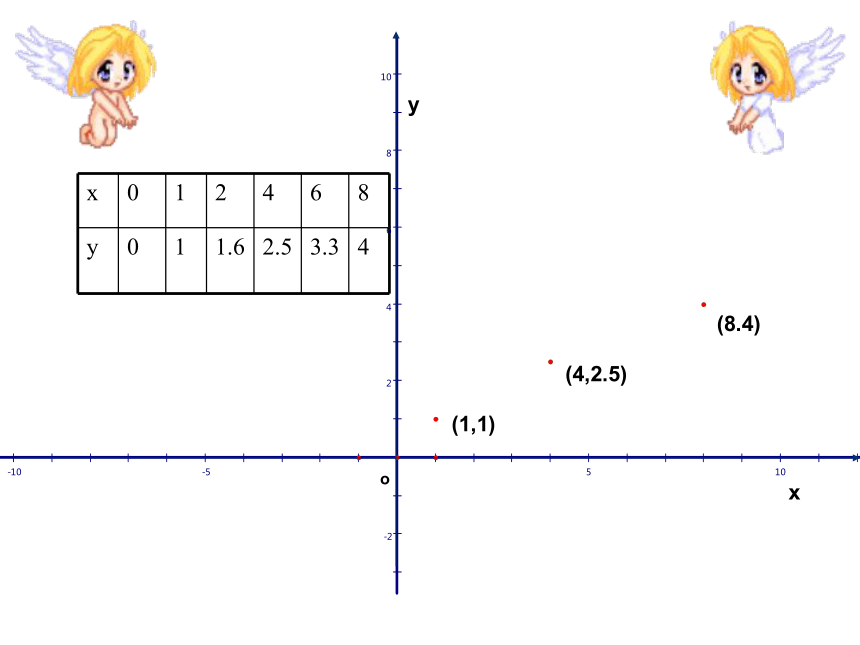
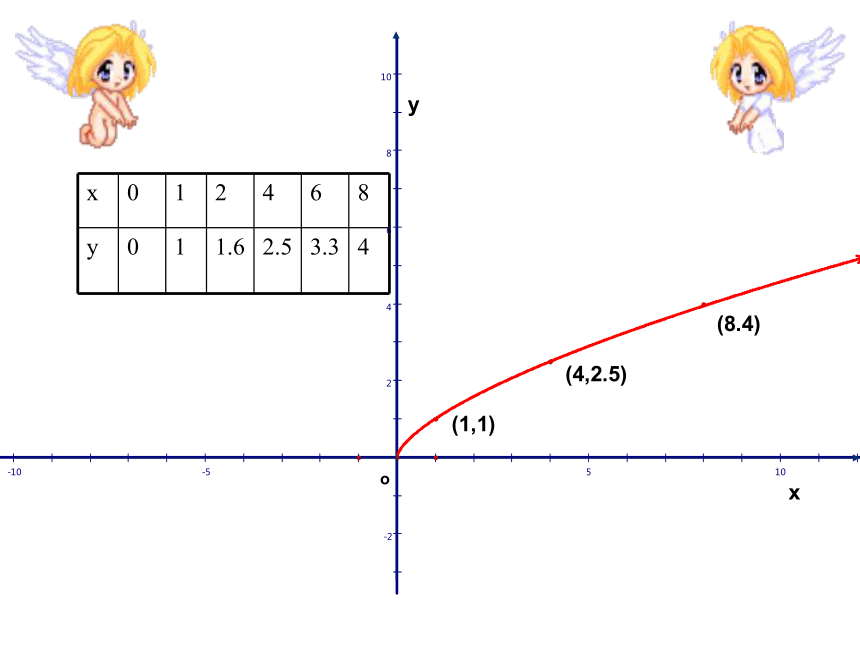
文档简介
课件39张PPT。幂函数的性质与图象授课人:孙宇上海市扬子中学问题引入 (1) 如果回收旧报纸每公斤1元,某班每年卖旧报纸x公斤,所得价钱y是关于x的函数 (2) 如果正方形的边长为x,面积y,这里y是关于x的函数;
(3) 如果正方体的边长为x, 正方体的体积为y, 这里y是关于x函数;
(4)如果一个正方形场地的面积为x, 这个正方形的边长为y,这里y是关于x的函数;
(5)如果某人x秒内骑车行驶了1km,他骑车的平均速度是y,这里y是关于x的函数.
我们先看几个具体问题: 1:以上各题目的函数关系分别是什么?
2:以上问题中的函数具有什么共同特征?一、幂函数的定义一般地,函数y = xK叫做幂函数,其中x是自变量,k是常数。(k∈Q)注 意1、幂函数的解析式必须是y = xK 的形式, 其特征可归纳为“两个系数为1,只有1项.2、定义域与k的值有关系.例1、下列函数中,哪几个函数是幂函数?
(1)y = (2)y=2x2
(3)y=2x (4)y=1
(5) y=x2 +2 (6) y=-x3答案:(1)(4) (1)奇偶性:∵定义域不关于原点对称, ∴为非奇非偶函数.于是 即f(x1)>f(x2)(2)单调性: 设任意x1、x2∈(0,+∞),且0<x1<x2, 所以 在(0,+∞)上是减函数例2研究幂函数 的定义域、奇偶性 和单调性,并作出图象解: 它的定义域是(0,+∞)定义域:(-∞,+∞)奇偶性:偶函数探 究 与 发 现例2:讨论函数 的定义域,作出它的图象,并根据图象说明函数的单调性、奇偶性及值域。在 上是增函数定义域: 在 上是减函数 值 域:奇偶性:偶函数单调性:作出下列函数的图象:y=x在第一象限内,函数图象的变化趋势与指数有什么关系?在第一象限内,
当k>0时,图象随x增大而上升。
当k<0时,图象随x增大而下降
不管指数是多少,图象都经过哪个定点?在第一象限内,
当k>0时,图象随x增大而上升。
当k<0时,图象随x增大而下降。图象都经过点(1,1)K>0时,图象还都过点(0,0)点幂函数的性质:1.所有的幂函数在(0,+∞)都有定义,并且函数图象都通过点(1,1);
幂函数的定义域、奇偶性、单调性,因函数式中k的不同而各异.3.如果k<0,则幂函数的图象过点(1,1),并在(0,+∞)上为减函数;
2.如果k>0,则幂函数的图象过点(0,0),(1,1)并在(0,+∞)上为增函数;
练习:
如果函数
是幂函数,且在区间(0,+∞)内是减函数,求满足条件的实数m的集合。
解:(1)y= x0.8在(0,∞)内是增函数,
∵5.2<5.3 ∴ 5.20.8 < 5.30.8
(2)y=x0.3在(0,∞)内是增函数
∵0.2<0.3∴ 0.20.3 <0.30.3(3)y=x-2/5在(0,∞)内是减函数
∵2.5<2.7∴ 2.5-2/5>2.7-2/5 练习<<>≤XyXy第一象限k<0时k>0时双曲线型0<k<1开口 向右抛物线型OOk<0画出函数在第一象限的图象后,再根据函数的奇偶性,画出函数在其他象限还有的图象K=0,直线型k>1开口向上型抛物线K=1练习: 如图所示,曲线是幂函数 y = xk 在第一象限内的图象,已知 k分别取 四个值,则相应图象依次为:________ 一般地,幂函数的图象在直线x=1
的右侧,大指数在上,小指数在下,
在Y轴与直线x =1之间正好相反。 C4C2C3C11y(A)(B)(I)(C)X(G)(H)(D)(J)(F)IGEBCAHJDF练习XXXXXXXXXOOOOOOOOOOyyyyyyyy(E)y小结
形如y=xk(k∈Q)
的函数叫做幂函数.3、思想与方法
小结1、幂函数的定义及图象特征?2、幂函数的性质3、思想与方法
k>0,在(0,+∞)上为增函数;
k<0,在(0,+∞)上为减函数
图象过定点(1,1)小结1、幂函数的定义及图象特征?2、幂函数的性质3、思想与方法
运用函数性质解决问题时,要想到数形结合的思想方法,寓数于形,赋形于数,互相利用,相得溢彰.作业:103页3
106页1,3再见
(3) 如果正方体的边长为x, 正方体的体积为y, 这里y是关于x函数;
(4)如果一个正方形场地的面积为x, 这个正方形的边长为y,这里y是关于x的函数;
(5)如果某人x秒内骑车行驶了1km,他骑车的平均速度是y,这里y是关于x的函数.
我们先看几个具体问题: 1:以上各题目的函数关系分别是什么?
2:以上问题中的函数具有什么共同特征?一、幂函数的定义一般地,函数y = xK叫做幂函数,其中x是自变量,k是常数。(k∈Q)注 意1、幂函数的解析式必须是y = xK 的形式, 其特征可归纳为“两个系数为1,只有1项.2、定义域与k的值有关系.例1、下列函数中,哪几个函数是幂函数?
(1)y = (2)y=2x2
(3)y=2x (4)y=1
(5) y=x2 +2 (6) y=-x3答案:(1)(4) (1)奇偶性:∵定义域不关于原点对称, ∴为非奇非偶函数.于是 即f(x1)>f(x2)(2)单调性: 设任意x1、x2∈(0,+∞),且0<x1<x2, 所以 在(0,+∞)上是减函数例2研究幂函数 的定义域、奇偶性 和单调性,并作出图象解: 它的定义域是(0,+∞)定义域:(-∞,+∞)奇偶性:偶函数探 究 与 发 现例2:讨论函数 的定义域,作出它的图象,并根据图象说明函数的单调性、奇偶性及值域。在 上是增函数定义域: 在 上是减函数 值 域:奇偶性:偶函数单调性:作出下列函数的图象:y=x在第一象限内,函数图象的变化趋势与指数有什么关系?在第一象限内,
当k>0时,图象随x增大而上升。
当k<0时,图象随x增大而下降
不管指数是多少,图象都经过哪个定点?在第一象限内,
当k>0时,图象随x增大而上升。
当k<0时,图象随x增大而下降。图象都经过点(1,1)K>0时,图象还都过点(0,0)点幂函数的性质:1.所有的幂函数在(0,+∞)都有定义,并且函数图象都通过点(1,1);
幂函数的定义域、奇偶性、单调性,因函数式中k的不同而各异.3.如果k<0,则幂函数的图象过点(1,1),并在(0,+∞)上为减函数;
2.如果k>0,则幂函数的图象过点(0,0),(1,1)并在(0,+∞)上为增函数;
练习:
如果函数
是幂函数,且在区间(0,+∞)内是减函数,求满足条件的实数m的集合。
解:(1)y= x0.8在(0,∞)内是增函数,
∵5.2<5.3 ∴ 5.20.8 < 5.30.8
(2)y=x0.3在(0,∞)内是增函数
∵0.2<0.3∴ 0.20.3 <0.30.3(3)y=x-2/5在(0,∞)内是减函数
∵2.5<2.7∴ 2.5-2/5>2.7-2/5 练习<<>≤XyXy第一象限k<0时k>0时双曲线型0<k<1开口 向右抛物线型OOk<0画出函数在第一象限的图象后,再根据函数的奇偶性,画出函数在其他象限还有的图象K=0,直线型k>1开口向上型抛物线K=1练习: 如图所示,曲线是幂函数 y = xk 在第一象限内的图象,已知 k分别取 四个值,则相应图象依次为:________ 一般地,幂函数的图象在直线x=1
的右侧,大指数在上,小指数在下,
在Y轴与直线x =1之间正好相反。 C4C2C3C11y(A)(B)(I)(C)X(G)(H)(D)(J)(F)IGEBCAHJDF练习XXXXXXXXXOOOOOOOOOOyyyyyyyy(E)y小结
形如y=xk(k∈Q)
的函数叫做幂函数.3、思想与方法
小结1、幂函数的定义及图象特征?2、幂函数的性质3、思想与方法
k>0,在(0,+∞)上为增函数;
k<0,在(0,+∞)上为减函数
图象过定点(1,1)小结1、幂函数的定义及图象特征?2、幂函数的性质3、思想与方法
运用函数性质解决问题时,要想到数形结合的思想方法,寓数于形,赋形于数,互相利用,相得溢彰.作业:103页3
106页1,3再见
