人教版七年级数学下册 8.4 三元一次方程组的解法 教学设计
文档属性
| 名称 | 人教版七年级数学下册 8.4 三元一次方程组的解法 教学设计 |  | |
| 格式 | docx | ||
| 文件大小 | 543.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-09 08:16:12 | ||
图片预览


文档简介
《三元一次方程组的解法》教学设计
一、课题及章节:人教版、七年级下册、 第八章第四节二、教学目标
1、知识与技能:了解三元一次方程组的概念,会解三元一次方程组。
2、过程与方法:在解三元一次方程组的过程中,进一步体会消元的思想和转化的思想。
3、情感态度与价值观:会针对方程组的特点探究最优解法,使学生体会探索的乐趣,增强学习兴趣。
三、教学重难点
1、教学重点:运用“消元”思想化三元一次方程组为二元一次方程组,进而化为一元一次 方程
2、教学难点:针对方程组的特点选择最优解法四、教学方法
教法:类比二元一次方程组的概念与解法,按照“实际问题—建立数学模型
(三元一次方程组)—类比、解释、应用、拓展”的模式展开本节课的教学。
学法:类比用代入法、加减法解二元一次方程组的过程与思想,沿用“消元” 这一核心思想,将“三元”化为“二元”,最后化为“一元”。
五、教具准备
多媒体展台、希沃课件、学案六、教学课时:1 课时
七、教学过程1、复习回顾
(1)游戏“眼力大比拼—方程划消”
二元一次方程组的特征:
①方程组中只含有 ;②每个方程中 的次数都是 1③共有 个方程
【设计意图】“方程划消”游戏是插入希沃 5 的触发动画、超链接实现的,然后进一步利用触发动画让学生回顾“二元、一次、方程组”三个关键词的意义。通
过游戏引起学生的兴趣,回顾二元一次方程组的特征,为后面通过“类比”得出
三元一次方程组作铺垫。
“温故而知新”
解方程组:2x y 4 ①
x y 2 ②
【设计意图】此处插入了希沃 5 中的蒙层、遮罩功能,使知识的呈现更生动、快捷。练习用代入法或加减法解二元一次方程组,体会“消元”思想,为将“三元” 转化为“二元”提供探究的思路。
“生活情境”
乐乐有 12 张面额分别为 1 元、2 元、5 元的纸币,共 22 元,其中 1 元纸
币的数量是 2 元纸币数量的 4 倍。求 1 元、2 元、5 元纸币各多少张? 分析:设 1 元、2 元、5 元纸币分别为 张、 张、 张
由“12 张”,可列方程:
由“共计 22 元”,可列方程:
由“1 元纸币币的数量是 2 元纸币数量的 4 倍”,可列方程:
师:此题中 X、Y、Z 要同时满足以上三个方程,故三个方程的共同的解,可以将三个方程联立起来,得到:
问:这是前面学习的二元一次方程组吗?
这就是今天要学习的新知识——三元一次方程组(引入课题)
【设计意图】通过生活中的实际问题引入,通俗易懂,学生容易理解,同时能体会到数学来源于生活。
2、创设情境、自主探究
x+y+z=12 ① 观察: x+2y+5z=22 ②
x=4y ③
思考:类比二元一次方程组的特征,上述方程组有什么特征?
特点是:①方程组中只含有 ;②每个方程中 的次数都是
;
③共有 个方程
像这样的方程叫做三元一次方程组.
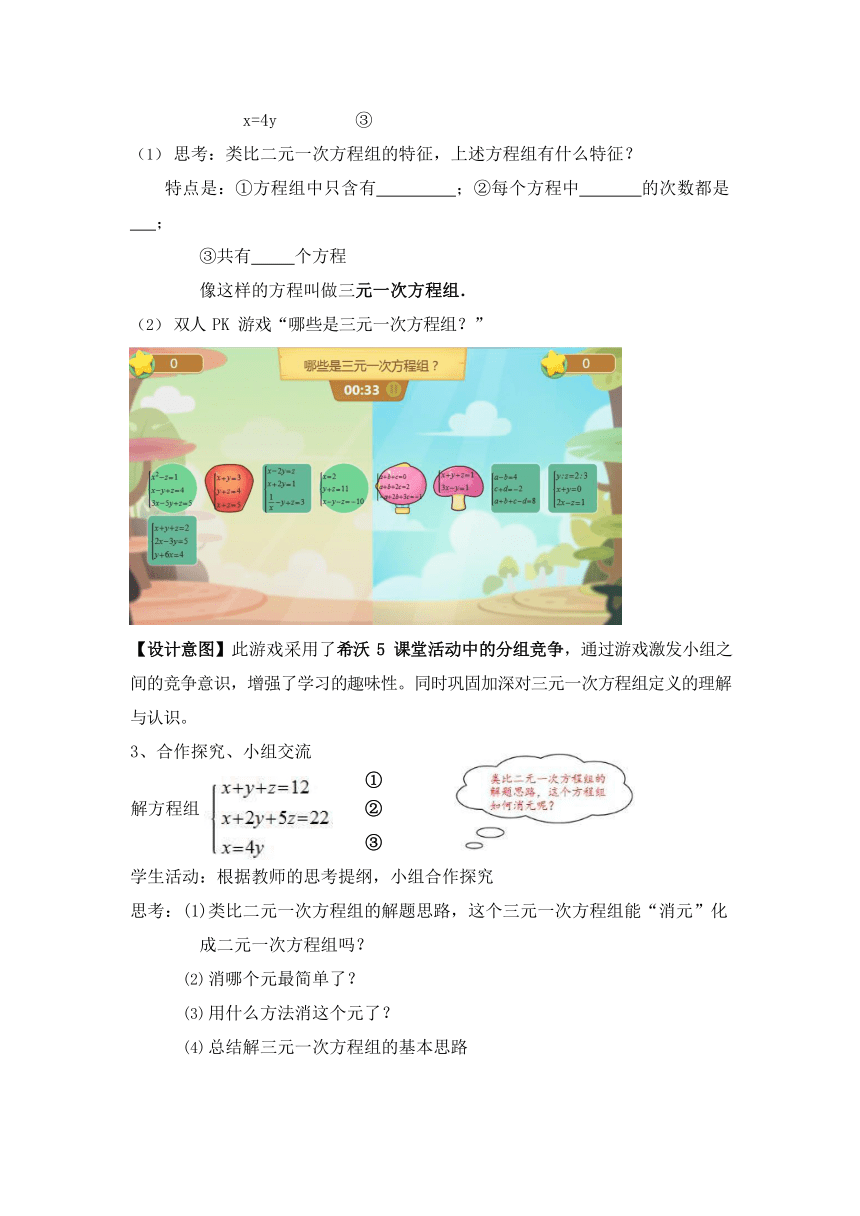
双人 PK 游戏“哪些是三元一次方程组?”
【设计意图】此游戏采用了希沃 5 课堂活动中的分组竞争,通过游戏激发小组之间的竞争意识,增强了学习的趣味性。同时巩固加深对三元一次方程组定义的理解与认识。
3、合作探究、小组交流
①
解方程组 ②
③
学生活动:根据教师的思考提纲,小组合作探究
思考:(1)类比二元一次方程组的解题思路,这个三元一次方程组能“消元”化成二元一次方程组吗?
消哪个元最简单了?
用什么方法消这个元了?
总结解三元一次方程组的基本思路
【设计意图】此处插入了流程图,通过教师思考提纲引导,学生通过小组合作探究,充分参与到知识方法的生成过程中,体会探究的乐趣,同时更加深入的体会到解题方法环环相扣、解题思想一脉相承。
4、学以致用、典例精析
例 1 解方程组 ①
②
③
【设计意图】通过师生合作探究,规范解题过程及格式。同时,通过探究使学生学会分析方程组特点,培养学生的归纳总结能力,选择最优的方法“消元”,初步体会数学中的优化思想。
“配对”游戏
【设计意图】此游戏采用了希沃 5 课堂活动中的知识配对,实现了“在学中玩”
的快乐学习理念,同时通过练习加深学生对选择最佳解法的认识,使解题过程更加简单高效。
“小试牛刀”
例 2 在等式 y=ax2+bx+c 中,当 x= -1 时,y=0;当 x=2 时,y=3;当 x=5 时,y=60, 求 a,b,c 的值.
【设计意图】通过经典题型的练习,使学生熟练掌握解三元一次方程组的方法。
5、变式探究、拓展提升
2x 3y k
已知方程组
3x 4 y k 11
的解 x、y 满足方程 5x y 3 ,求 k 的值。
学生活动:自主探究,seewolink 授课助手拍照展示多种方法成果,学生讲解。最后微课讲解总结。
方法一:建立三元一次方程组方法二:“整体代入”思想
【设计意图】此环节先使用 link 授课助手,拍照上传学生的不同成果,然后学生代表上台讲解,然后播放解题技巧的微课,让学生从不同角度理解三元一次方程组的建立,让学生充分探索不同的解题方法,体会特殊方程、系数的巧妙解法, 拓宽学生的解题思路,加深对“消元”的理解。
6、归纳总结、整合建构
本节课大家学到了哪些知识?应用了哪些数学方法?体现了哪些数学思想?
【设计意图】小结插入了希沃 5 中的思维导图,清晰的呈现本节课的知识脉络、方法及思想;同时使用蒙层、橡皮擦工具,使“消元”这一核心思想的呈现更生动有趣。
7、作业布置
课本 106 页第 2、4、5
选做题:课本 112 页第 11 题八、板书设计
三元一次方程组的解法
1、定义
2、基本思想:三元一次方程组 例 1 解方程组
消元
二元一次方程组
消元 解:
一元一次方程3、方法:代入法、加减法
4、数学思想:消元、转化、整体代入
九、教学预期、教学反思
通过本节课的学习,希望学生能熟练掌握三元一次方程组的解法,同时体会“消元”、“转化”等数学思想在知识生成过程中的指导作用。由于化三元为二元的方法多样、灵活,希望学生能善于观察方程及系数特点,灵活采用简捷的方法消元,利用这种逐个消去未知数的方法还可以解多元方程组,但“消元”的思想始终不变,最终目标是转化为一元一次方程。
一、课题及章节:人教版、七年级下册、 第八章第四节二、教学目标
1、知识与技能:了解三元一次方程组的概念,会解三元一次方程组。
2、过程与方法:在解三元一次方程组的过程中,进一步体会消元的思想和转化的思想。
3、情感态度与价值观:会针对方程组的特点探究最优解法,使学生体会探索的乐趣,增强学习兴趣。
三、教学重难点
1、教学重点:运用“消元”思想化三元一次方程组为二元一次方程组,进而化为一元一次 方程
2、教学难点:针对方程组的特点选择最优解法四、教学方法
教法:类比二元一次方程组的概念与解法,按照“实际问题—建立数学模型
(三元一次方程组)—类比、解释、应用、拓展”的模式展开本节课的教学。
学法:类比用代入法、加减法解二元一次方程组的过程与思想,沿用“消元” 这一核心思想,将“三元”化为“二元”,最后化为“一元”。
五、教具准备
多媒体展台、希沃课件、学案六、教学课时:1 课时
七、教学过程1、复习回顾
(1)游戏“眼力大比拼—方程划消”
二元一次方程组的特征:
①方程组中只含有 ;②每个方程中 的次数都是 1③共有 个方程
【设计意图】“方程划消”游戏是插入希沃 5 的触发动画、超链接实现的,然后进一步利用触发动画让学生回顾“二元、一次、方程组”三个关键词的意义。通
过游戏引起学生的兴趣,回顾二元一次方程组的特征,为后面通过“类比”得出
三元一次方程组作铺垫。
“温故而知新”
解方程组:2x y 4 ①
x y 2 ②
【设计意图】此处插入了希沃 5 中的蒙层、遮罩功能,使知识的呈现更生动、快捷。练习用代入法或加减法解二元一次方程组,体会“消元”思想,为将“三元” 转化为“二元”提供探究的思路。
“生活情境”
乐乐有 12 张面额分别为 1 元、2 元、5 元的纸币,共 22 元,其中 1 元纸
币的数量是 2 元纸币数量的 4 倍。求 1 元、2 元、5 元纸币各多少张? 分析:设 1 元、2 元、5 元纸币分别为 张、 张、 张
由“12 张”,可列方程:
由“共计 22 元”,可列方程:
由“1 元纸币币的数量是 2 元纸币数量的 4 倍”,可列方程:
师:此题中 X、Y、Z 要同时满足以上三个方程,故三个方程的共同的解,可以将三个方程联立起来,得到:
问:这是前面学习的二元一次方程组吗?
这就是今天要学习的新知识——三元一次方程组(引入课题)
【设计意图】通过生活中的实际问题引入,通俗易懂,学生容易理解,同时能体会到数学来源于生活。
2、创设情境、自主探究
x+y+z=12 ① 观察: x+2y+5z=22 ②
x=4y ③
思考:类比二元一次方程组的特征,上述方程组有什么特征?
特点是:①方程组中只含有 ;②每个方程中 的次数都是
;
③共有 个方程
像这样的方程叫做三元一次方程组.
双人 PK 游戏“哪些是三元一次方程组?”
【设计意图】此游戏采用了希沃 5 课堂活动中的分组竞争,通过游戏激发小组之间的竞争意识,增强了学习的趣味性。同时巩固加深对三元一次方程组定义的理解与认识。
3、合作探究、小组交流
①
解方程组 ②
③
学生活动:根据教师的思考提纲,小组合作探究
思考:(1)类比二元一次方程组的解题思路,这个三元一次方程组能“消元”化成二元一次方程组吗?
消哪个元最简单了?
用什么方法消这个元了?
总结解三元一次方程组的基本思路
【设计意图】此处插入了流程图,通过教师思考提纲引导,学生通过小组合作探究,充分参与到知识方法的生成过程中,体会探究的乐趣,同时更加深入的体会到解题方法环环相扣、解题思想一脉相承。
4、学以致用、典例精析
例 1 解方程组 ①
②
③
【设计意图】通过师生合作探究,规范解题过程及格式。同时,通过探究使学生学会分析方程组特点,培养学生的归纳总结能力,选择最优的方法“消元”,初步体会数学中的优化思想。
“配对”游戏
【设计意图】此游戏采用了希沃 5 课堂活动中的知识配对,实现了“在学中玩”
的快乐学习理念,同时通过练习加深学生对选择最佳解法的认识,使解题过程更加简单高效。
“小试牛刀”
例 2 在等式 y=ax2+bx+c 中,当 x= -1 时,y=0;当 x=2 时,y=3;当 x=5 时,y=60, 求 a,b,c 的值.
【设计意图】通过经典题型的练习,使学生熟练掌握解三元一次方程组的方法。
5、变式探究、拓展提升
2x 3y k
已知方程组
3x 4 y k 11
的解 x、y 满足方程 5x y 3 ,求 k 的值。
学生活动:自主探究,seewolink 授课助手拍照展示多种方法成果,学生讲解。最后微课讲解总结。
方法一:建立三元一次方程组方法二:“整体代入”思想
【设计意图】此环节先使用 link 授课助手,拍照上传学生的不同成果,然后学生代表上台讲解,然后播放解题技巧的微课,让学生从不同角度理解三元一次方程组的建立,让学生充分探索不同的解题方法,体会特殊方程、系数的巧妙解法, 拓宽学生的解题思路,加深对“消元”的理解。
6、归纳总结、整合建构
本节课大家学到了哪些知识?应用了哪些数学方法?体现了哪些数学思想?
【设计意图】小结插入了希沃 5 中的思维导图,清晰的呈现本节课的知识脉络、方法及思想;同时使用蒙层、橡皮擦工具,使“消元”这一核心思想的呈现更生动有趣。
7、作业布置
课本 106 页第 2、4、5
选做题:课本 112 页第 11 题八、板书设计
三元一次方程组的解法
1、定义
2、基本思想:三元一次方程组 例 1 解方程组
消元
二元一次方程组
消元 解:
一元一次方程3、方法:代入法、加减法
4、数学思想:消元、转化、整体代入
九、教学预期、教学反思
通过本节课的学习,希望学生能熟练掌握三元一次方程组的解法,同时体会“消元”、“转化”等数学思想在知识生成过程中的指导作用。由于化三元为二元的方法多样、灵活,希望学生能善于观察方程及系数特点,灵活采用简捷的方法消元,利用这种逐个消去未知数的方法还可以解多元方程组,但“消元”的思想始终不变,最终目标是转化为一元一次方程。
