第七单元 第3课时 利用平移解决问题(教学课件)-四年级数学下册人教版(共28张PPT)
文档属性
| 名称 | 第七单元 第3课时 利用平移解决问题(教学课件)-四年级数学下册人教版(共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-09 05:44:00 | ||
图片预览





文档简介
(共28张PPT)
第3课时
利用平移知识求不规则图形的面积
小学数学·四年级(下)·RJ
在剪一剪,移一移的过程中,渗透转化是思想,灵活解决实际问题,并在解决实际问题的过程中 ,发展学生的空间观念。
通过运用转化思想,把不规则图形转化为规则图形,并能用平移的知识解决不规则图形的面积的问题。
在具体的情境中,感受平移现象在现实生活中的应用,在应用中体验数学的价值。
运用平移的方法解决简单不规则图形的面积问题。
利用平移知识解决问题。
生活中处处有数学的思想,让学生在学习的过程中体验数学的美。
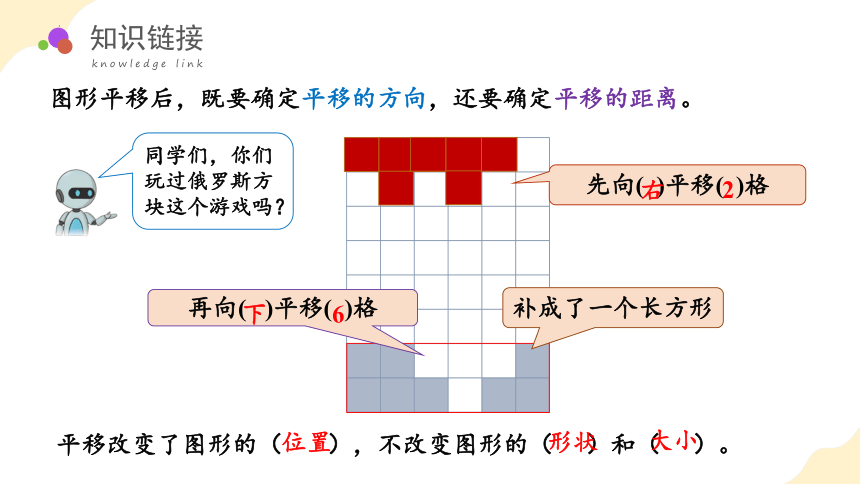
补成了一个长方形
先向( )平移( )格
再向( )平移( )格
同学们,你们玩过俄罗斯方块这个游戏吗?
右
2
下
6
平移改变了图形的( ),不改变图形的( )和( )。
位置
大小
形状
图形平移后,既要确定平移的方向,还要确定平移的距离。
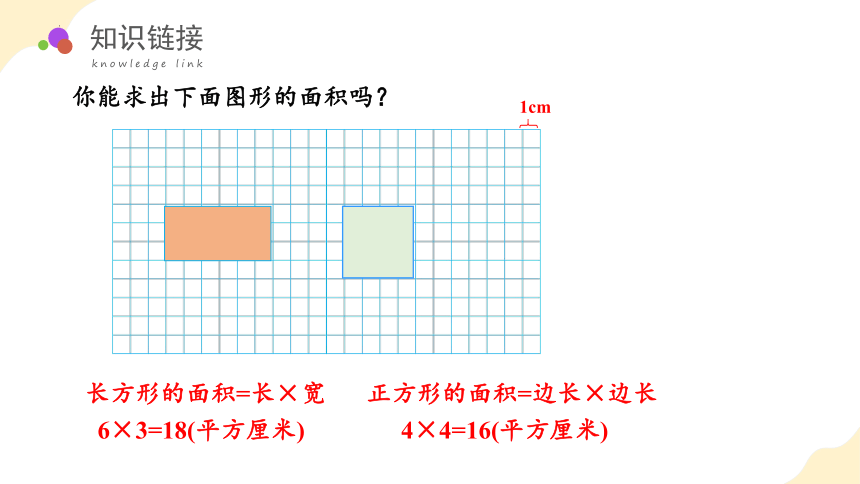
你能求出下面图形的面积吗?
长方形的面积=长×宽
正方形的面积=边长×边长
6×3=18(平方厘米)
4×4=16(平方厘米)
1cm
运用平移求不规则图形的面积
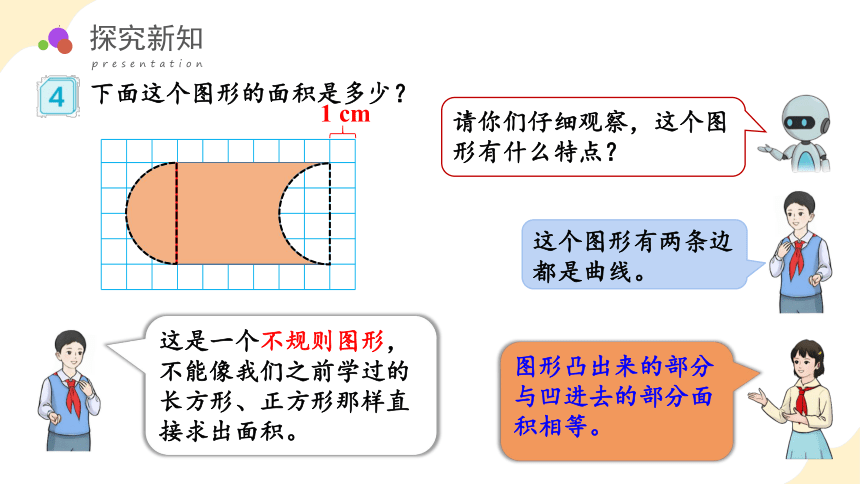
下面这个图形的面积是多少?
这是一个不规则图形,不能像我们之前学过的长方形、正方形那样直接求出面积。
1 cm
请你们仔细观察,这个图形有什么特点?
图形凸出来的部分与凹进去的部分面积相等。
这个图形有两条边都是曲线。
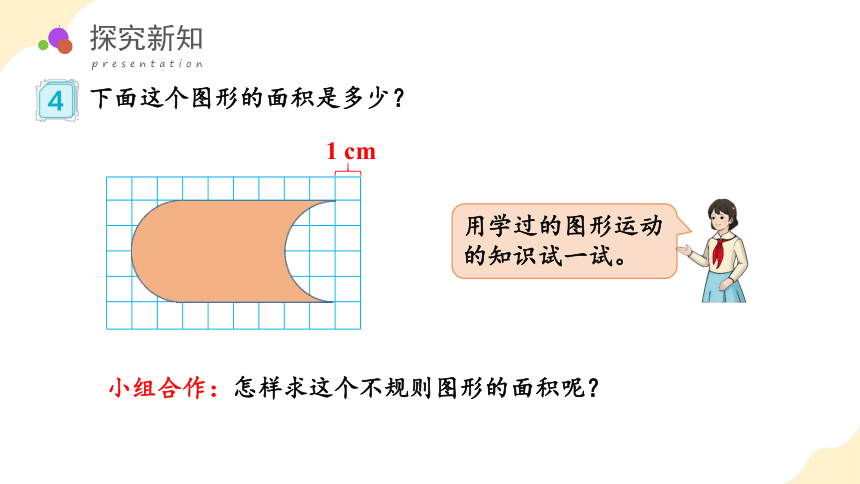
下面这个图形的面积是多少?
1 cm
小组合作:怎样求这个不规则图形的面积呢?
用学过的图形运动的知识试一试。
下面这个图形的面积是多少?
1cm
“数”的方法:数一数这个图形占多少个方格,当数到不是整格时当作半格计算。
1cm
18个整格
√
√
√
√
√
√
√
√
√
√
√
√
12个半格
=6个整格
24cm
1cm
“补”的方法:将左右不足一整格的补成一整格,然后再算。
8×4=32cm
32-8=24cm
下面这个图形的面积是多少?
下面这个图形的面积是多少?
1cm
1.沿虚线将凸出的半圆切开。
2.将左边凸出部分向右平移6格。
6格
3.转化成一个长6格、宽是4格的长方形。
长6cm
宽4cm
“移”的方法:
6×4=24cm
6×4=24(cm )
1 cm
1 cm
转化后的长方形与原图形形状不同,但是面积相等,求长方形的面积就相当于是求原图形的面积。
答:这个图形的面积是24 cm 。
长6cm
宽4cm
割补、平移
不规则图形
规则图形
转化
面积不变
求一些不规则图形的面积时,可以利用割补、平移等方法,将不规则图形转化成规则图形,再根据公式计算。
我们利用了哪种运动方式,使图形发生了怎样的变化,从而求出了不规则图形的面积?
灵活运用平移解决实际问题
1. 求这个图形的周长和面积(每个小正方形的边长是1cm)。
(5+4)×2=18(cm)
答:这个图形的周长是18cm。
(5+2)×2=14(cm )
答:这个图形的面积是14cm 。
2.如图所示,在一块长26 m,宽16 m的长方形花坛里修了一条宽2 m的曲曲折折的观赏小路。求花坛的实际面积。
①
②
16 – 2
26 – 2
(26 – 2) ×(16 – 2)=24×14
=336(m )
答:花坛的实际面积是336 m 。
将②先向上平移2 m,再向左平移2 m,就可以拼成一个长方形。
2 m
2 m
归纳总结:
观察图形的特点,利用平移的性质,把不规则的图形转化为规则的图形。从而求得图形的周长或面积。
归纳总结
想一想,说一说:在刚才利用平移求面积过程中,有哪些注意事项?
将图形分割,利用平移求图形面积时,图形形状改变了,但面积不变。
运用平移的方法,把不规则图形转化成规则图形,体现了转化思想。
达标练习,巩固成果
教材第84页“做一做”
1.画一画,量一量,算出下面这个火箭的面积。
9 cm
3 cm
9×3=27(cm )
答:这个火箭的面积是27 cm 。
观察发现:将右边的三角形平移到左边,原图就变成了一个长方形。
教材第85页“练习二十一”第3题
2. 涂色部分占整个图形的几分之几?
( )
( )
( )
( )
1
3
( )
( )
1
2
3
1
3.想一想,怎样才能算出下面图形的周长。
教材第85页“练习二十一”第4题
5cm
10cm
周长:(5+10)×2=30cm
通过平移不规则图形的边,把它转化成规则的长方形。
4. 下面是一个楼梯的截面图,楼梯共10级,每级台阶的高都是20cm,这个楼梯的截面周长是多少厘米?
20×10=200(cm)
(200+180)×2=760(cm)
答:这个楼梯的截面周长是760厘米。
5. 下面的长方形土地是由两块边长为4 m的正方形土地拼成的,蓝色部分种茉莉花,每平方米种8棵。一共能种多少棵茉莉花?
4×4=16(平方米) 16×8=128(棵)
答:一共能种128棵茉莉花。
转化图形时,可以将部分图形进行平移,也可以对部分边进行平移。
求一些不规则图形的周长或面积时,可以利用割补、平移等方法,将不规则图形转化成规则图形,再根据公式计算。
1. 绘制本节课知识的思维导图;
2. 完成《分层作业》。
第3课时
利用平移知识求不规则图形的面积
小学数学·四年级(下)·RJ
在剪一剪,移一移的过程中,渗透转化是思想,灵活解决实际问题,并在解决实际问题的过程中 ,发展学生的空间观念。
通过运用转化思想,把不规则图形转化为规则图形,并能用平移的知识解决不规则图形的面积的问题。
在具体的情境中,感受平移现象在现实生活中的应用,在应用中体验数学的价值。
运用平移的方法解决简单不规则图形的面积问题。
利用平移知识解决问题。
生活中处处有数学的思想,让学生在学习的过程中体验数学的美。
补成了一个长方形
先向( )平移( )格
再向( )平移( )格
同学们,你们玩过俄罗斯方块这个游戏吗?
右
2
下
6
平移改变了图形的( ),不改变图形的( )和( )。
位置
大小
形状
图形平移后,既要确定平移的方向,还要确定平移的距离。
你能求出下面图形的面积吗?
长方形的面积=长×宽
正方形的面积=边长×边长
6×3=18(平方厘米)
4×4=16(平方厘米)
1cm
运用平移求不规则图形的面积
下面这个图形的面积是多少?
这是一个不规则图形,不能像我们之前学过的长方形、正方形那样直接求出面积。
1 cm
请你们仔细观察,这个图形有什么特点?
图形凸出来的部分与凹进去的部分面积相等。
这个图形有两条边都是曲线。
下面这个图形的面积是多少?
1 cm
小组合作:怎样求这个不规则图形的面积呢?
用学过的图形运动的知识试一试。
下面这个图形的面积是多少?
1cm
“数”的方法:数一数这个图形占多少个方格,当数到不是整格时当作半格计算。
1cm
18个整格
√
√
√
√
√
√
√
√
√
√
√
√
12个半格
=6个整格
24cm
1cm
“补”的方法:将左右不足一整格的补成一整格,然后再算。
8×4=32cm
32-8=24cm
下面这个图形的面积是多少?
下面这个图形的面积是多少?
1cm
1.沿虚线将凸出的半圆切开。
2.将左边凸出部分向右平移6格。
6格
3.转化成一个长6格、宽是4格的长方形。
长6cm
宽4cm
“移”的方法:
6×4=24cm
6×4=24(cm )
1 cm
1 cm
转化后的长方形与原图形形状不同,但是面积相等,求长方形的面积就相当于是求原图形的面积。
答:这个图形的面积是24 cm 。
长6cm
宽4cm
割补、平移
不规则图形
规则图形
转化
面积不变
求一些不规则图形的面积时,可以利用割补、平移等方法,将不规则图形转化成规则图形,再根据公式计算。
我们利用了哪种运动方式,使图形发生了怎样的变化,从而求出了不规则图形的面积?
灵活运用平移解决实际问题
1. 求这个图形的周长和面积(每个小正方形的边长是1cm)。
(5+4)×2=18(cm)
答:这个图形的周长是18cm。
(5+2)×2=14(cm )
答:这个图形的面积是14cm 。
2.如图所示,在一块长26 m,宽16 m的长方形花坛里修了一条宽2 m的曲曲折折的观赏小路。求花坛的实际面积。
①
②
16 – 2
26 – 2
(26 – 2) ×(16 – 2)=24×14
=336(m )
答:花坛的实际面积是336 m 。
将②先向上平移2 m,再向左平移2 m,就可以拼成一个长方形。
2 m
2 m
归纳总结:
观察图形的特点,利用平移的性质,把不规则的图形转化为规则的图形。从而求得图形的周长或面积。
归纳总结
想一想,说一说:在刚才利用平移求面积过程中,有哪些注意事项?
将图形分割,利用平移求图形面积时,图形形状改变了,但面积不变。
运用平移的方法,把不规则图形转化成规则图形,体现了转化思想。
达标练习,巩固成果
教材第84页“做一做”
1.画一画,量一量,算出下面这个火箭的面积。
9 cm
3 cm
9×3=27(cm )
答:这个火箭的面积是27 cm 。
观察发现:将右边的三角形平移到左边,原图就变成了一个长方形。
教材第85页“练习二十一”第3题
2. 涂色部分占整个图形的几分之几?
( )
( )
( )
( )
1
3
( )
( )
1
2
3
1
3.想一想,怎样才能算出下面图形的周长。
教材第85页“练习二十一”第4题
5cm
10cm
周长:(5+10)×2=30cm
通过平移不规则图形的边,把它转化成规则的长方形。
4. 下面是一个楼梯的截面图,楼梯共10级,每级台阶的高都是20cm,这个楼梯的截面周长是多少厘米?
20×10=200(cm)
(200+180)×2=760(cm)
答:这个楼梯的截面周长是760厘米。
5. 下面的长方形土地是由两块边长为4 m的正方形土地拼成的,蓝色部分种茉莉花,每平方米种8棵。一共能种多少棵茉莉花?
4×4=16(平方米) 16×8=128(棵)
答:一共能种128棵茉莉花。
转化图形时,可以将部分图形进行平移,也可以对部分边进行平移。
求一些不规则图形的周长或面积时,可以利用割补、平移等方法,将不规则图形转化成规则图形,再根据公式计算。
1. 绘制本节课知识的思维导图;
2. 完成《分层作业》。
