第七单元 第1课时 轴对称(教学课件)-四年级数学下册人教版(共35张PPT)
文档属性
| 名称 | 第七单元 第1课时 轴对称(教学课件)-四年级数学下册人教版(共35张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-09 05:44:57 | ||
图片预览









文档简介
(共35张PPT)
第1课时
轴对称图形的性质及画法
小学数学·四年级(下)·RJ
让学生在活动中欣赏图形的变换美,进一步感受轴对称在生活中的应用,体会学习数学的价值。
在观察、操作等活动中,进一步认识轴对称图形及其对称轴,体会轴对称图形的特征和性质,并能在方格纸上补全一个轴对称图形。
在探究轴对称图形性质的过程中体会对应思想,在总结画法的过程中提高学生的抽象、概括能力,发展空间观念。
掌握轴对称图形的特征和性质。
能在方格纸上画出轴对称图形的另一半。
让学生经历“做”数学的过程,在操作中理解规律,感受知识间的联系。
它们都是一类特殊的图形——轴对称图形。
观察这些物体,你能发现它们都有什么共同特征?
这些图案中蕴含着哪些数学知识,今天我们来了解更多轴对称的知识!
进一步认识轴对称图形及其对称轴
看一看、想一想:你发现了什么?
像这样,对折后两边能够完全重合的图形就是轴对称图形。
折痕所在的这条直线就是对称轴。
对称轴两边的图形完全重合了。
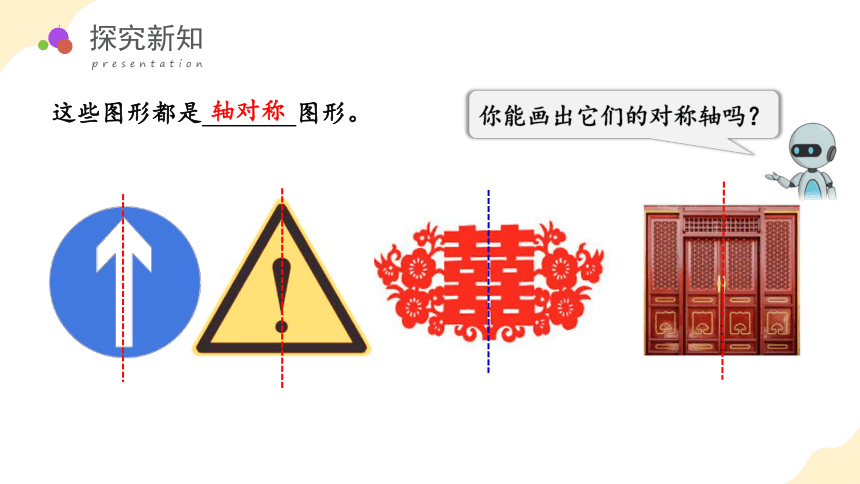
这些图形都是 图形。
轴对称
你能画出它们的对称轴吗?
你还见过哪些轴对称图形?画出它们的对称轴。
发现:有的图形只有一条对称轴,有的图形有多条对称轴。
生活中很多图形都利用了轴对称的对称美。
探究轴对称图形的性质
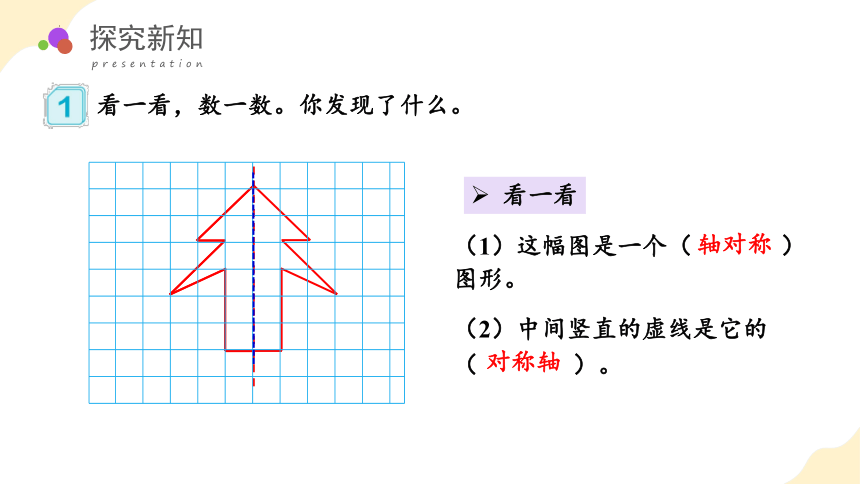
(1)这幅图是一个( ) 图形。
轴对称
(2)中间竖直的虚线是它的( )。
对称轴
看一看,数一数。你发现了什么。
看一看
看一看,数一数。你发现了什么。
A′
A
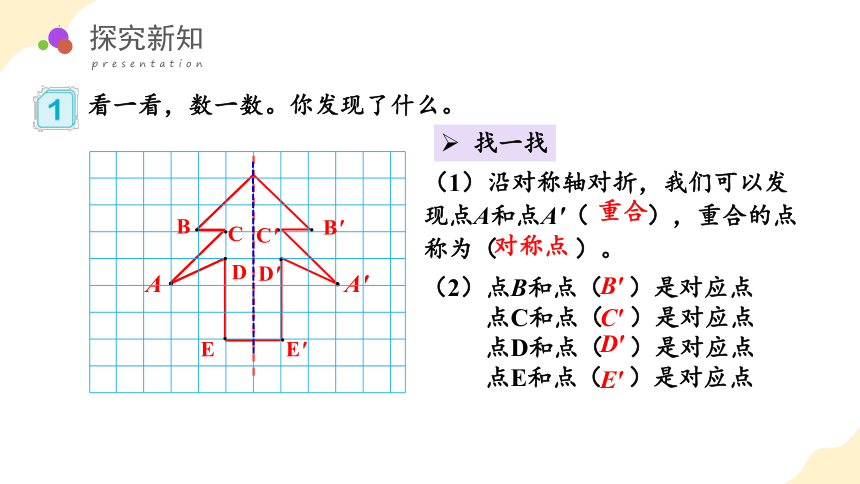
找一找
(1)沿对称轴对折,我们可以发现点A和点A′( ),重合的点称为( )。
重合
对称点
B
B′
C
C′
D
D′
E
E′
(2)点B和点( )是对应点
点C和点( )是对应点
点D和点( )是对应点
点E和点( )是对应点
B′
C′
D′
E′
看一看,数一数。你发现了什么。
连接对称点,发现对称点的连线与对称轴垂直。
将这两个对称点连接起来,你能发现什么?
A′
A
E
B
B′
C
C′
D
D′
E′
(2)点B 和点B′到对称轴的距离都是( )个小格,距离( )。
看一看,数一数。你发现了什么。
A′
A
E
B
B′
C
C′
D
D′
E′
数一数
3格
3格
2格
2格
(1)点A与点A′到对称轴的距离都是
( )个小格,距离( )。
相等
相等
3
2
我的发现:轴对称图形上两个对称点到对称轴的方格数(距离)是相等的。
看一看,数一数。你发现了什么。
A′
A
E
B
B′
C
C′
D
D′
E′
填一填
对称点 A和A′ B和B′ C和C′ D和D′ E和E′
到对称轴的距离
3
小
格
2
小
格
1
小
格
1
小
格
1
小
格
我的结论是:每组对称点到对称轴的距离都是相等的。
运用轴对称图形的特征和性质解决问题
根据对称轴补全下面这个轴对称图形。
这是五角星的一半,虚线是它的对称轴。补全就是要画出五角星的另一半。
理解题意。
怎样画得又好又快?
根据对称轴补全下面这个轴对称图形。
2.画图方法
想一想:
(1)先画什么?再画什么?
(2)每条线段应该画多长?
根据对称轴补全下面这个轴对称图形。
2.画图方法
①“找”,找出图形上条线段的端点;并用字母表示出来。
A
B
D
E
A
'
B
'
D
'
E
'
C
C
'
F
F
'
1格
1格
②“定”,根据对称轴确定每一个端点的对称点;
4格
4格
2格
2格
3格
3格
③“连”,依次连接这些对称点,得到轴对称图形的另一半。
A
B
C
D
B′
C′
·
·
·
D′
E′
·
1.“找”,找出图形上每条线段的端点或交叉点。
E
F
说一说:你是如何根据对称轴,补全下面这个图形的
2.“定”,根据对称轴确定每一个端点(或交叉点)的对称点。
3.“连”,按照原图形的形状顺次连接这些对称点,得到轴对称图形的另一半。
轴对称图形画法并不难,找准关键点是关键。点轴距离要按格算,才能找得准对称点。
依次连接各对称点,轴对称图形准确现。
达标练习,巩固成果
教材第80页做一做 第1题
1. 说一说,轴对称图形有哪些特点?
答:轴对称图形沿着对称轴对折,两侧的图形能够完全重合;
轴对称图形对称点的连线与对称轴垂直;
轴对称图形对称点到对称轴的距离相等。
2. 试一试,画出下面这个轴对称图形的另一半。
教材第80页做一做 第2题
第一步:标出点A和点B;
第二步:通过数格找到
对称点A' 和B';
第三步:依次连线。
A
5格
5格
A'
B'
B
3格
3格
3.剪下附页上的图形,先折一折,再画出下面图形的对称轴,看看能画几条。
2条
4条
3条
6条
教材第81页“练习二十”第1题
我国戏剧的脸谱多种多样,但基本上都是轴对称图形!
4. 剪下附页上的脸谱,贴在下面的空白处。
教材第81页“练习二十”第2题
对折4次,可以把一张纸平均分成16份,就可以剪出8只同样的蝴蝶。
对折3次,可以把一张纸平均分成8份,就可以剪出4只同样的蝴蝶。
5. 像下面这样把一张纸连续对折3次,剪出的是什么图案?对折4次呢?
想:对折1次可以把一张纸平均分成2份,就可以剪出一只完整的蝴蝶。
对折3次,是4只蝴蝶。
对折4次,是8只蝴蝶。
教材第81页“练习二十”第3题
6. 分别画出下面两个轴对称图形的另一半。
A
B
C
A′
B′
C′
A
A′
B
C
D
E
B′
C′
D′
E′
一“找”
二“定”
三“连”
教材第82页“练习二十”第5题
7. 下面图形各是从哪张纸上剪下来的?连一连。
教材第82页“练习二十”第6题
教材第82页“练习二十”第7题
8.你能画出下面图形的另一半吗?试一试。
A
B
C
D
A′
D′
(1)找出图形中每条线段的端点,分别命名为A、B、C、D。
其中A、D两个端点在对称轴上,分别与其对称点位置重合。
8.你能画出下面图形的另一半吗?试一试。
(2)找出点B、C的对称点。
可以过端点(如点B)作对称轴的垂线,量出点B到垂足之间的距离,根据这一距离在对称轴的另一侧找到点B的对称点B′,如图所示。
同理可找出点C的对称点。
A
B
C
D
B′
C′
A′
D′
教材第82页“练习二十”第7题
(3)顺次连接各个对应点,就可以画出已知图形的另一半。
A
B
C
D
B′
C′
A′
D′
8.你能画出下面图形的另一半吗?试一试。
教材第82页“练习二十”第7题
A
B
C
D
E
F
A′
B′
C′
D′
E′
F′
按照刚才的方法,分别过点B、C、D、E作对称轴的垂线,并测量各点到对称轴的距离,再在另一侧找到对应点,顺次连接对应点,就可以得到图形的另一半。
8.你能画出下面图形的另一半吗?试一试。
轴图形对称的特点:
◇对称轴两侧的图形完全重合。
◇轴对称图形的对称点到对称轴的方格数(距离)相等。
◇对称点的连线与对称轴垂直。
利用对称轴补全轴对称图形的方法:
①“找”:找出图形上每条线段的端点。
②“定”:根据对称轴确定每一个端点的对称点。
③“连”:依次连接这些对称点。
1. 绘制本节课知识的思维导图;
2. 完成《分层作业》。
第1课时
轴对称图形的性质及画法
小学数学·四年级(下)·RJ
让学生在活动中欣赏图形的变换美,进一步感受轴对称在生活中的应用,体会学习数学的价值。
在观察、操作等活动中,进一步认识轴对称图形及其对称轴,体会轴对称图形的特征和性质,并能在方格纸上补全一个轴对称图形。
在探究轴对称图形性质的过程中体会对应思想,在总结画法的过程中提高学生的抽象、概括能力,发展空间观念。
掌握轴对称图形的特征和性质。
能在方格纸上画出轴对称图形的另一半。
让学生经历“做”数学的过程,在操作中理解规律,感受知识间的联系。
它们都是一类特殊的图形——轴对称图形。
观察这些物体,你能发现它们都有什么共同特征?
这些图案中蕴含着哪些数学知识,今天我们来了解更多轴对称的知识!
进一步认识轴对称图形及其对称轴
看一看、想一想:你发现了什么?
像这样,对折后两边能够完全重合的图形就是轴对称图形。
折痕所在的这条直线就是对称轴。
对称轴两边的图形完全重合了。
这些图形都是 图形。
轴对称
你能画出它们的对称轴吗?
你还见过哪些轴对称图形?画出它们的对称轴。
发现:有的图形只有一条对称轴,有的图形有多条对称轴。
生活中很多图形都利用了轴对称的对称美。
探究轴对称图形的性质
(1)这幅图是一个( ) 图形。
轴对称
(2)中间竖直的虚线是它的( )。
对称轴
看一看,数一数。你发现了什么。
看一看
看一看,数一数。你发现了什么。
A′
A
找一找
(1)沿对称轴对折,我们可以发现点A和点A′( ),重合的点称为( )。
重合
对称点
B
B′
C
C′
D
D′
E
E′
(2)点B和点( )是对应点
点C和点( )是对应点
点D和点( )是对应点
点E和点( )是对应点
B′
C′
D′
E′
看一看,数一数。你发现了什么。
连接对称点,发现对称点的连线与对称轴垂直。
将这两个对称点连接起来,你能发现什么?
A′
A
E
B
B′
C
C′
D
D′
E′
(2)点B 和点B′到对称轴的距离都是( )个小格,距离( )。
看一看,数一数。你发现了什么。
A′
A
E
B
B′
C
C′
D
D′
E′
数一数
3格
3格
2格
2格
(1)点A与点A′到对称轴的距离都是
( )个小格,距离( )。
相等
相等
3
2
我的发现:轴对称图形上两个对称点到对称轴的方格数(距离)是相等的。
看一看,数一数。你发现了什么。
A′
A
E
B
B′
C
C′
D
D′
E′
填一填
对称点 A和A′ B和B′ C和C′ D和D′ E和E′
到对称轴的距离
3
小
格
2
小
格
1
小
格
1
小
格
1
小
格
我的结论是:每组对称点到对称轴的距离都是相等的。
运用轴对称图形的特征和性质解决问题
根据对称轴补全下面这个轴对称图形。
这是五角星的一半,虚线是它的对称轴。补全就是要画出五角星的另一半。
理解题意。
怎样画得又好又快?
根据对称轴补全下面这个轴对称图形。
2.画图方法
想一想:
(1)先画什么?再画什么?
(2)每条线段应该画多长?
根据对称轴补全下面这个轴对称图形。
2.画图方法
①“找”,找出图形上条线段的端点;并用字母表示出来。
A
B
D
E
A
'
B
'
D
'
E
'
C
C
'
F
F
'
1格
1格
②“定”,根据对称轴确定每一个端点的对称点;
4格
4格
2格
2格
3格
3格
③“连”,依次连接这些对称点,得到轴对称图形的另一半。
A
B
C
D
B′
C′
·
·
·
D′
E′
·
1.“找”,找出图形上每条线段的端点或交叉点。
E
F
说一说:你是如何根据对称轴,补全下面这个图形的
2.“定”,根据对称轴确定每一个端点(或交叉点)的对称点。
3.“连”,按照原图形的形状顺次连接这些对称点,得到轴对称图形的另一半。
轴对称图形画法并不难,找准关键点是关键。点轴距离要按格算,才能找得准对称点。
依次连接各对称点,轴对称图形准确现。
达标练习,巩固成果
教材第80页做一做 第1题
1. 说一说,轴对称图形有哪些特点?
答:轴对称图形沿着对称轴对折,两侧的图形能够完全重合;
轴对称图形对称点的连线与对称轴垂直;
轴对称图形对称点到对称轴的距离相等。
2. 试一试,画出下面这个轴对称图形的另一半。
教材第80页做一做 第2题
第一步:标出点A和点B;
第二步:通过数格找到
对称点A' 和B';
第三步:依次连线。
A
5格
5格
A'
B'
B
3格
3格
3.剪下附页上的图形,先折一折,再画出下面图形的对称轴,看看能画几条。
2条
4条
3条
6条
教材第81页“练习二十”第1题
我国戏剧的脸谱多种多样,但基本上都是轴对称图形!
4. 剪下附页上的脸谱,贴在下面的空白处。
教材第81页“练习二十”第2题
对折4次,可以把一张纸平均分成16份,就可以剪出8只同样的蝴蝶。
对折3次,可以把一张纸平均分成8份,就可以剪出4只同样的蝴蝶。
5. 像下面这样把一张纸连续对折3次,剪出的是什么图案?对折4次呢?
想:对折1次可以把一张纸平均分成2份,就可以剪出一只完整的蝴蝶。
对折3次,是4只蝴蝶。
对折4次,是8只蝴蝶。
教材第81页“练习二十”第3题
6. 分别画出下面两个轴对称图形的另一半。
A
B
C
A′
B′
C′
A
A′
B
C
D
E
B′
C′
D′
E′
一“找”
二“定”
三“连”
教材第82页“练习二十”第5题
7. 下面图形各是从哪张纸上剪下来的?连一连。
教材第82页“练习二十”第6题
教材第82页“练习二十”第7题
8.你能画出下面图形的另一半吗?试一试。
A
B
C
D
A′
D′
(1)找出图形中每条线段的端点,分别命名为A、B、C、D。
其中A、D两个端点在对称轴上,分别与其对称点位置重合。
8.你能画出下面图形的另一半吗?试一试。
(2)找出点B、C的对称点。
可以过端点(如点B)作对称轴的垂线,量出点B到垂足之间的距离,根据这一距离在对称轴的另一侧找到点B的对称点B′,如图所示。
同理可找出点C的对称点。
A
B
C
D
B′
C′
A′
D′
教材第82页“练习二十”第7题
(3)顺次连接各个对应点,就可以画出已知图形的另一半。
A
B
C
D
B′
C′
A′
D′
8.你能画出下面图形的另一半吗?试一试。
教材第82页“练习二十”第7题
A
B
C
D
E
F
A′
B′
C′
D′
E′
F′
按照刚才的方法,分别过点B、C、D、E作对称轴的垂线,并测量各点到对称轴的距离,再在另一侧找到对应点,顺次连接对应点,就可以得到图形的另一半。
8.你能画出下面图形的另一半吗?试一试。
轴图形对称的特点:
◇对称轴两侧的图形完全重合。
◇轴对称图形的对称点到对称轴的方格数(距离)相等。
◇对称点的连线与对称轴垂直。
利用对称轴补全轴对称图形的方法:
①“找”:找出图形上每条线段的端点。
②“定”:根据对称轴确定每一个端点的对称点。
③“连”:依次连接这些对称点。
1. 绘制本节课知识的思维导图;
2. 完成《分层作业》。
