2.3双曲线-双曲线的标准方程[上学期]
图片预览



文档简介
课件15张PPT。今日导学P 34~37预习目标:2.3双曲线-双曲线的标准方程预习要求:思考以下问题,并组织语言清楚地表述答案:
①双曲线的定义是什么?
②你能根据双曲线的定义推导出双曲线的方程来吗?(想一想:椭圆方程是怎样建立的?) 你的方法和结果与课本一样吗?谁的对?谁的好?为什么?
③记忆双曲线的标准方程,能默写!并明确方程中的各字母都表示什么?思考:给你什么条件,你能写出一个双曲线的标准方程?
作业预告: 课本P37 习题2.3(1) 1,4,5ask双曲线的标准方程
(第一课时)今日导学P 34~37预习目标:2.3双曲线_双曲线及其标准方程预习要求:思考以下问题,并组织语言清楚地表述答案:
①双曲线的定义是什么?
②你能根据双曲线的定义推导出双曲线的方程来吗? (想一想:椭圆方程是怎样建立的?)你的方法和结果与课本一样吗?谁的对?谁的好?为什么?
③记忆双曲线的标准方程,能默写!并明确方程中的各字母都表示什么?思考:给你什么条件,你能写出一个双曲线的标准方程?
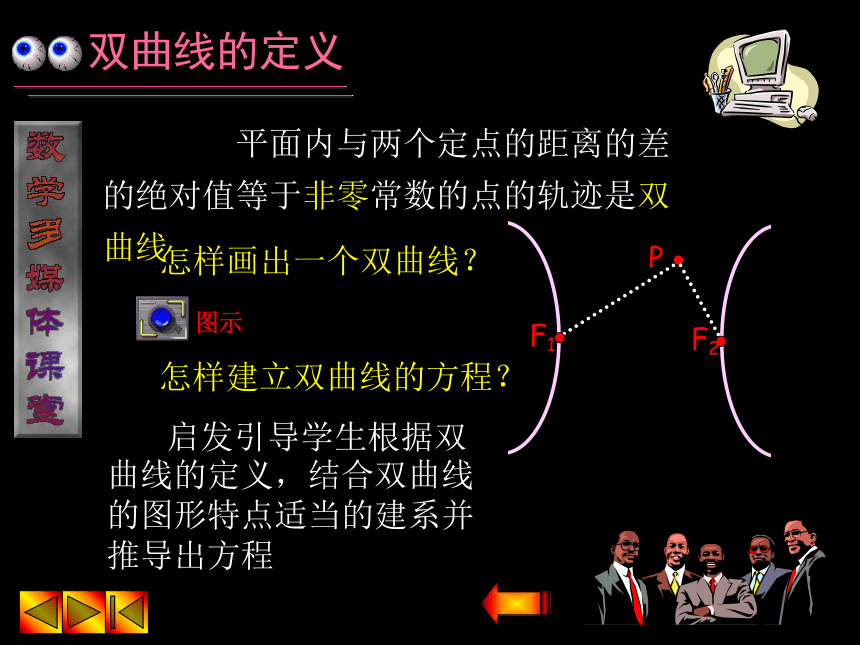
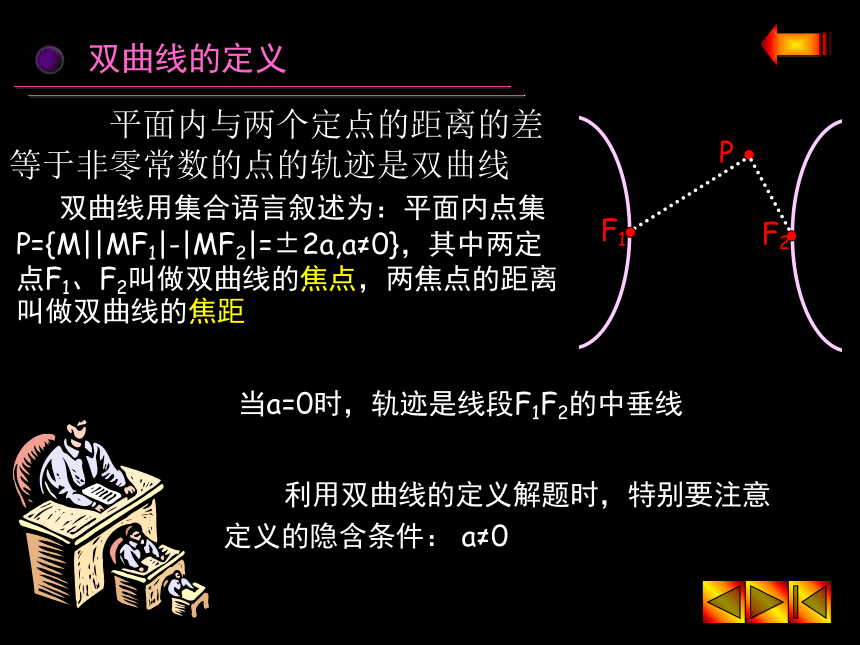
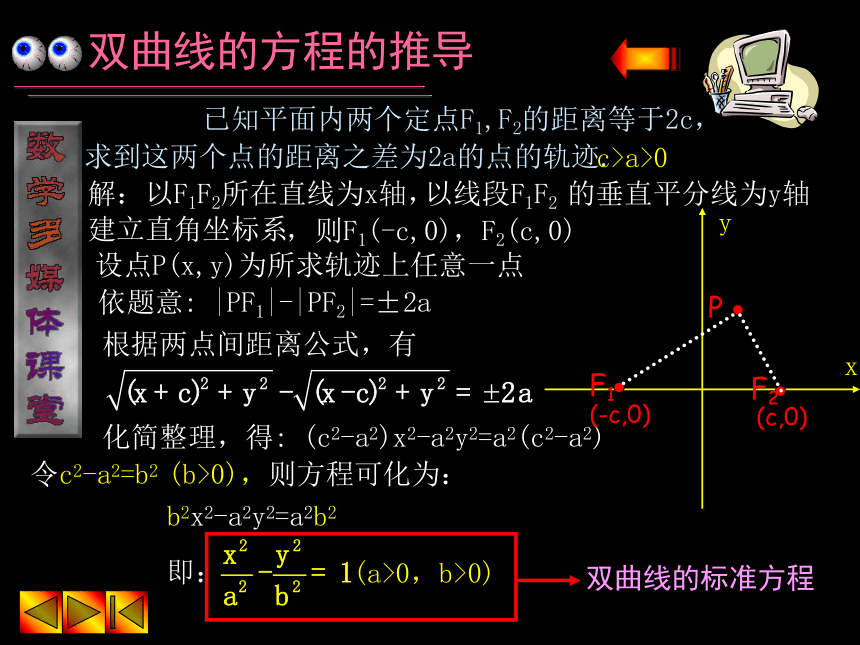
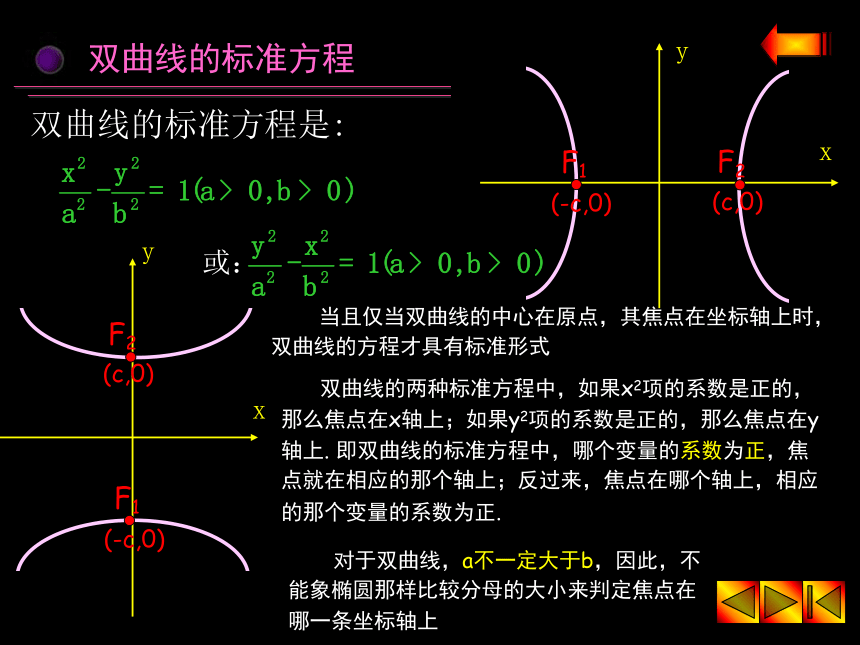
④阅读例1,例2 作业预告:课本P37 习题2.3(1) 1,4,5双曲线的定义 平面内与两个定点的距离的差的绝对值等于非零常数的点的轨迹是双曲线1怎样画出一个双曲线?怎样建立双曲线的方程? 启发引导学生根据双曲线的定义,结合双曲线的图形特点适当的建系并推导出方程双曲线的定义当a=0时,轨迹是线段F1F2的中垂线 利用双曲线的定义解题时,特别要注意定义的隐含条件: a≠0 平面内与两个定点的距离的差等于非零常数的点的轨迹是双曲线 双曲线用集合语言叙述为:平面内点集P={M||MF1|-|MF2|=±2a,a≠0},其中两定点F1、F2叫做双曲线的焦点,两焦点的距离叫做双曲线的焦距双曲线的方程的推导 已知平面内两个定点F1,F2的距离等于2c,求到这两个点的距离之差为2a的点的轨迹.yx解:以F1F2所在直线为x轴,以线段F1F2 的垂直平分线为y轴建立直角坐标系,则F1(-c,0),F2(c,0)设点P(x,y)为所求轨迹上任意一点依题意: |PF1|-|PF2|=±2a根据两点间距离公式,有化简整理,得: (c2-a2)x2-a2y2=a2(c2-a2)c>a>0(-c,0)(c,0)令c2-a2=b2 (b>0),则方程可化为:b2x2-a2y2=a2b2(a>0,b>0)双曲线的标准方程是:双曲线的标准方程 双曲线的两种标准方程中,如果x2项的系数是正的,那么焦点在x轴上;如果y2项的系数是正的,那么焦点在y轴上. 即双曲线的标准方程中,哪个变量的系数为正,焦点就在相应的那个轴上;反过来,焦点在哪个轴上,相应的那个变量的系数为正. 当且仅当双曲线的中心在原点,其焦点在坐标轴上时,双曲线的方程才具有标准形式 对于双曲线,a不一定大于b,因此,不能象椭圆那样比较分母的大小来判定焦点在哪一条坐标轴上双曲线的标准方程(-c,0)和(c,0)(0,-c)和(0,c)如果焦点在x轴上,焦点坐标是:
如果焦点在y轴上,焦点坐标是:特别注意双曲线与椭圆的差异:
在椭圆中,有a2=b2+c2,a最大
在双曲线中,有c2=a2+b2,c最大课堂练习 平面内两个定点的距离等于10,一个动点M到这两个定点的距离的差等于6,建立适当的坐标系,写出动点M的轨迹方程.答:设以两定点为端点的线段是F1F2, 以F1F2所在直线为y轴,以其中垂线为 x轴,建立直角坐标系,则所求动点M 的轨迹方程是: 如果双曲线4x2-y2+64=0上一点P到它的一个焦点的距离等于1,则点P到另一个焦点的距离是 .课堂练习17 如果双曲线4x2-y2+64=0上一点P到它的一个焦点的距离等于20,则点P到另一个焦点的距离是 .36或4 用待定系数法求双曲线标准方程一般分以下三步:解题规律(学生对例1阅读后,启发引导学生得出如下结论)根据已知条件,建立关于a、b的方程;解方程求出a、b,然后代入所设方程 思考:如果焦点位置不确定在哪个坐标轴上,怎么设双曲线的方程?课堂练习课本36页练习1写出适合下列条件的双曲线的标准方程:
1、 c=5,b=3,焦点在x轴上: ;
2、焦点为(0,-6)、(0,6),且a=3 : ;
3、过点 ( ,1 ) 、( 4 , -3 ): ; 1. 双曲线的定义、焦点、焦距:
2.双曲线的标准方程: 课堂小结 3.重点:双曲线的定义和标准方程
4.难点:双曲线标准方程的推导
焦点在x轴上时焦点在y轴上时作业反馈作业反馈课本P37 习题2.3 1,4,5深圳市龙华中学张渭玲 E-mail:weilzw@163.com
①双曲线的定义是什么?
②你能根据双曲线的定义推导出双曲线的方程来吗?(想一想:椭圆方程是怎样建立的?) 你的方法和结果与课本一样吗?谁的对?谁的好?为什么?
③记忆双曲线的标准方程,能默写!并明确方程中的各字母都表示什么?思考:给你什么条件,你能写出一个双曲线的标准方程?
作业预告: 课本P37 习题2.3(1) 1,4,5ask双曲线的标准方程
(第一课时)今日导学P 34~37预习目标:2.3双曲线_双曲线及其标准方程预习要求:思考以下问题,并组织语言清楚地表述答案:
①双曲线的定义是什么?
②你能根据双曲线的定义推导出双曲线的方程来吗? (想一想:椭圆方程是怎样建立的?)你的方法和结果与课本一样吗?谁的对?谁的好?为什么?
③记忆双曲线的标准方程,能默写!并明确方程中的各字母都表示什么?思考:给你什么条件,你能写出一个双曲线的标准方程?
④阅读例1,例2 作业预告:课本P37 习题2.3(1) 1,4,5双曲线的定义 平面内与两个定点的距离的差的绝对值等于非零常数的点的轨迹是双曲线1怎样画出一个双曲线?怎样建立双曲线的方程? 启发引导学生根据双曲线的定义,结合双曲线的图形特点适当的建系并推导出方程双曲线的定义当a=0时,轨迹是线段F1F2的中垂线 利用双曲线的定义解题时,特别要注意定义的隐含条件: a≠0 平面内与两个定点的距离的差等于非零常数的点的轨迹是双曲线 双曲线用集合语言叙述为:平面内点集P={M||MF1|-|MF2|=±2a,a≠0},其中两定点F1、F2叫做双曲线的焦点,两焦点的距离叫做双曲线的焦距双曲线的方程的推导 已知平面内两个定点F1,F2的距离等于2c,求到这两个点的距离之差为2a的点的轨迹.yx解:以F1F2所在直线为x轴,以线段F1F2 的垂直平分线为y轴建立直角坐标系,则F1(-c,0),F2(c,0)设点P(x,y)为所求轨迹上任意一点依题意: |PF1|-|PF2|=±2a根据两点间距离公式,有化简整理,得: (c2-a2)x2-a2y2=a2(c2-a2)c>a>0(-c,0)(c,0)令c2-a2=b2 (b>0),则方程可化为:b2x2-a2y2=a2b2(a>0,b>0)双曲线的标准方程是:双曲线的标准方程 双曲线的两种标准方程中,如果x2项的系数是正的,那么焦点在x轴上;如果y2项的系数是正的,那么焦点在y轴上. 即双曲线的标准方程中,哪个变量的系数为正,焦点就在相应的那个轴上;反过来,焦点在哪个轴上,相应的那个变量的系数为正. 当且仅当双曲线的中心在原点,其焦点在坐标轴上时,双曲线的方程才具有标准形式 对于双曲线,a不一定大于b,因此,不能象椭圆那样比较分母的大小来判定焦点在哪一条坐标轴上双曲线的标准方程(-c,0)和(c,0)(0,-c)和(0,c)如果焦点在x轴上,焦点坐标是:
如果焦点在y轴上,焦点坐标是:特别注意双曲线与椭圆的差异:
在椭圆中,有a2=b2+c2,a最大
在双曲线中,有c2=a2+b2,c最大课堂练习 平面内两个定点的距离等于10,一个动点M到这两个定点的距离的差等于6,建立适当的坐标系,写出动点M的轨迹方程.答:设以两定点为端点的线段是F1F2, 以F1F2所在直线为y轴,以其中垂线为 x轴,建立直角坐标系,则所求动点M 的轨迹方程是: 如果双曲线4x2-y2+64=0上一点P到它的一个焦点的距离等于1,则点P到另一个焦点的距离是 .课堂练习17 如果双曲线4x2-y2+64=0上一点P到它的一个焦点的距离等于20,则点P到另一个焦点的距离是 .36或4 用待定系数法求双曲线标准方程一般分以下三步:解题规律(学生对例1阅读后,启发引导学生得出如下结论)根据已知条件,建立关于a、b的方程;解方程求出a、b,然后代入所设方程 思考:如果焦点位置不确定在哪个坐标轴上,怎么设双曲线的方程?课堂练习课本36页练习1写出适合下列条件的双曲线的标准方程:
1、 c=5,b=3,焦点在x轴上: ;
2、焦点为(0,-6)、(0,6),且a=3 : ;
3、过点 ( ,1 ) 、( 4 , -3 ): ; 1. 双曲线的定义、焦点、焦距:
2.双曲线的标准方程: 课堂小结 3.重点:双曲线的定义和标准方程
4.难点:双曲线标准方程的推导
焦点在x轴上时焦点在y轴上时作业反馈作业反馈课本P37 习题2.3 1,4,5深圳市龙华中学张渭玲 E-mail:weilzw@163.com
