六年级下册数学毕业总复习课件-第五章图形与几何第一课时 人教新课标(共44张PPT)
文档属性
| 名称 | 六年级下册数学毕业总复习课件-第五章图形与几何第一课时 人教新课标(共44张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-09 10:06:33 | ||
图片预览









文档简介
(共44张PPT)
第五章 图形与几何
第一课时 图形的认识
知识要点梳理
1.线与角
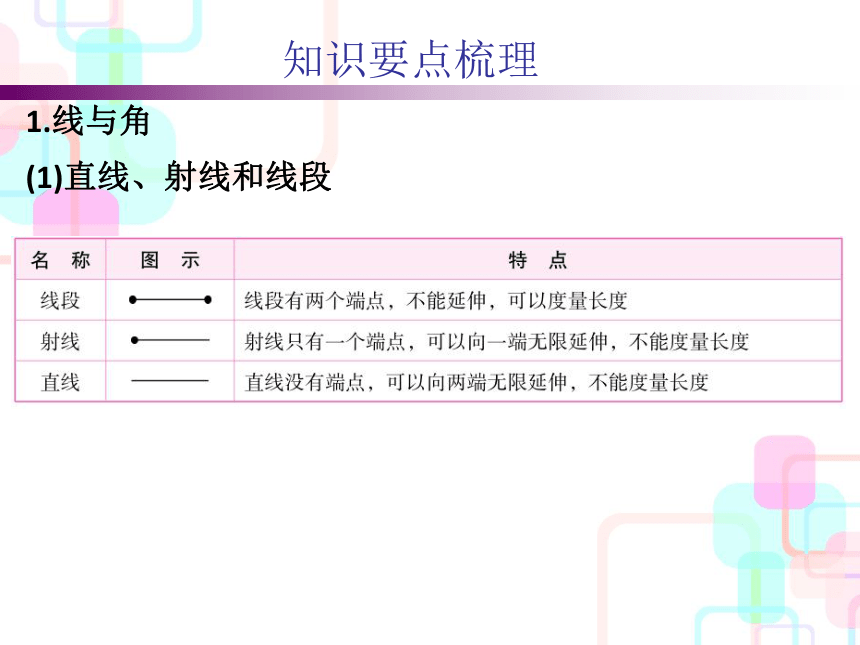
(1)直线、射线和线段
(2)垂直与平行
①垂直:两条直线相交成直角时,这两条直线互相垂直。其中一条直线叫做另一条直线的垂线,这两条直线的交点叫做垂足。
②平行线:在同一平面内,不相交的两条直线叫做平行线。平行线之间的距离处处相等。
③点到直线的距离:从直线外一点到这条直线所画的垂直线段的长,叫做这个点到直线的距离。
④同一平面内的两条直线不是平行就是相交(垂直是相交的特例)。
(3)垂线的基本性质
①过直线上或直线外一点,有且只有一条直线和已知直线垂直。
②从直线外一点到这条直线上各点所连的线段中,垂线段最短。
2. 角
(1)角的意义:从一点引出的两条射线所组成的图形叫做角。角的大小与两边的长短无关,与两边叉开的大小有关。
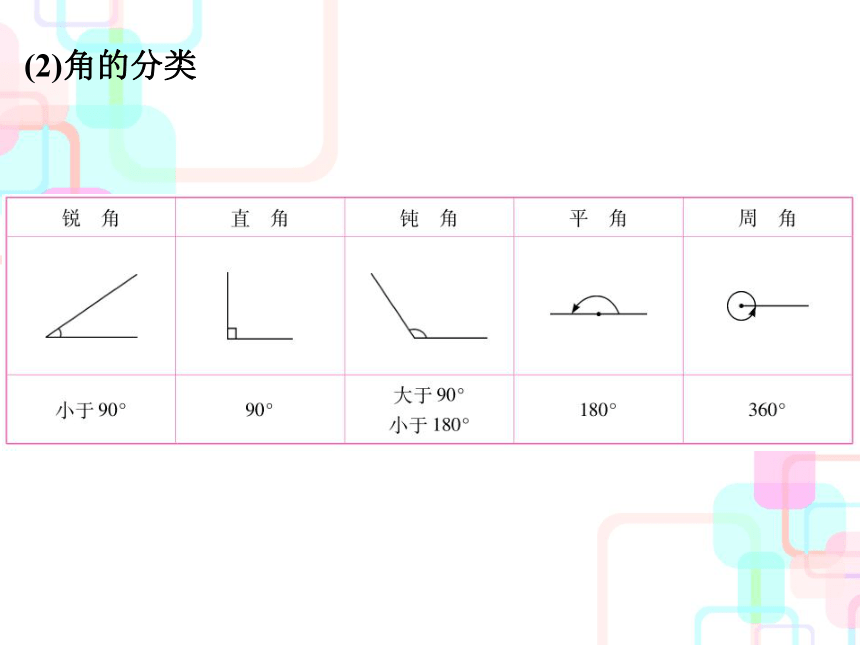
(2)角的分类
二、平面图形
1. 三角形
(1)三角形的定义:由3条线段围成的图形(每相邻两条线段的端点相连)叫做三角形。
(2)三角形有三条边、三个顶点、三个角。
(3)从三角形的一个顶点到它的对边作一条垂线,顶点和垂足之间的线段叫做三角形的高,这条对边叫做三角形的底。三角形有3条高。
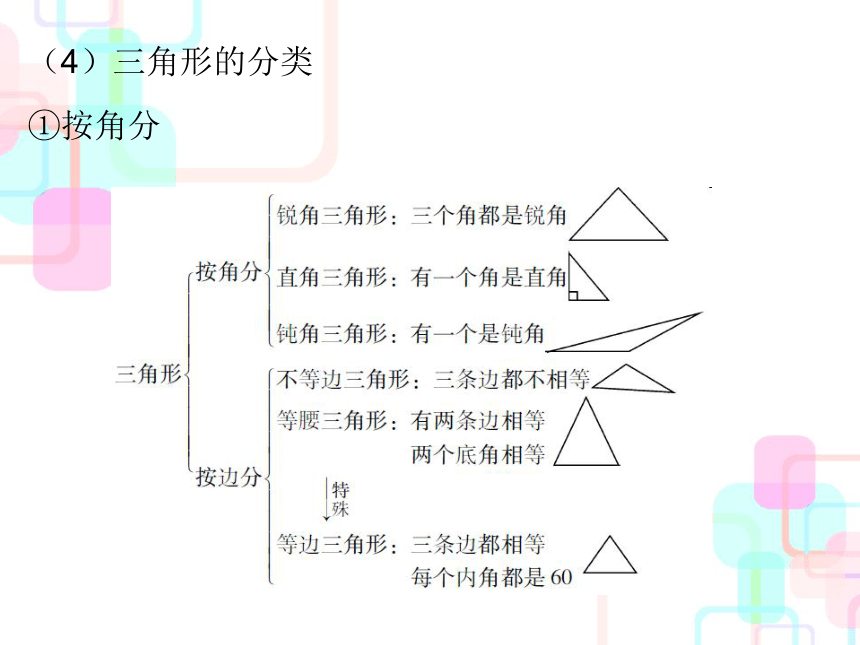
(4)三角形的分类
①按角分
(5)等边三角形是特殊的等腰三角形,
它们的关系如右图所示。
(6)三角形的特殊性质:三角形具有
稳定性。
(7)三角形的内角和是180°。
(8)三角形任意两条边的和大于第三
边。
2. 四边形
3. 圆
(1)圆的认识:平面上的一种曲线图形。圆中心的一点叫
做圆心,一般用字母O表示。
①半径:连接圆心和圆上任意一点的线段叫做半径,一般用r表示。
②在同一个圆里,有无数条半径,每条半径的长度都相等。
③通过圆心并且两端都在圆上的线段叫做直径,一般用d表示。
④同一个圆里有无数条直径,所有的直径都相等。
⑤同一个圆里,直径等于半径长度的两倍,即d=2r,或
r= 。
⑥圆心决定圆的位置,半径决定圆的大小。直径是圆中最长的线段。
⑦圆有无数条对称轴。
4. 扇形
(1)扇形的定义:一条弧和经过这条弧两端的两条半径所围成的图形叫做扇形。
(2)圆上AB两点之间的部分叫做弧,读作“弧AB”,记作“AB”。
(3)顶点在圆心的角叫做圆心角。
(4)在同一个圆中,扇形的大小与这个扇形的圆心角的大小有关。以半圆为弧的扇形的圆心角是180度,以1/4圆为弧的扇形的圆心角是90度。
(5)扇形有1条对称轴。
三、立体图形
1. 长方体和正方体
(1)顶点:棱和棱的交点。 棱:面和面相交的线段。 相交于一个顶点的三条棱的长度分别叫做长方体的长、宽、高。 把长方体放在桌面上,最多只能看到三个面。
(2)正方体是长、宽、高都相等的长方体,是特殊的长方体。
(3)长方体和正方体的关系:
2. 圆柱和圆锥
典例精析及训练
【例1】画一画。
(1)过N点作AB的垂线。 (2)过P点作AB的平行线。
(3)画出下面各图AB边上的高。
题型一
精析:画垂线、平行线和作图形的高都是必须掌握的技能。(1)用一把三角尺就可以画已知直线的垂线。方法:使三角尺的直角边与已知直线重合,沿重合的直线平移三角尺,使三角尺的另一条直角边和N点重合,过N点沿直角边向已知直线画直线即可。(2)用三角尺平移可以画出已知直线的平行线。方法:把三角尺的一条直角边与已知直线重合,用直尺紧靠三角尺的另一条直角边,沿直尺平移三角尺,原来与已知直线重合的直角边与已知点重合,过点沿三角尺的直角边画直线即可。(3)在作图形的高时,注意垂足应落在AB边上,高一般用虚线来表示,要标出垂足。根据画垂线的方法,用三角板的直角边作图,既快又准确。
答案:(1)
(2)
(3)
举一反三
1. 从直线外一点到这条直线可以画无数条线段,其中最短的是和这条直线( )的线段。
2. 在同一个平面内画已知直线的垂线,可以画( )条,如果过一点画已知直线的垂线,则只能画( )条。
3. 过P点画出直线AB的平行线和垂线。
垂直
无数
1
略
4. 路线设计。
(1)请你画一条从实验室到教学楼最近的路。
(2)请你画一条从实验室到操场最近的路。
略
题型二
【例2】直线a,b,c在同一平面内,a与b互相垂直,b与c互相垂直,那么a与c( )。
A. 垂直 B. 平行 C.平行或垂直
精析:此例题主要考查两直线在同一平面内的位置关系。根据之前所学,我们知道,在同一平面内,两直线的位置关系是相交或平行。本题中,三条直线在同一平面内,因为a与b互相垂直,b与c互相垂直,根据垂直于同一条直线的两直线平行,则可以判断a与c互相平行。因此应该选择答案B。
答案:B
举一反三
5. 长方形相邻的两条边互相( ),相对的两条边互相( )。
6. 两条直线相交成直角时,这两条直线就( )。
7. 判断:不相交的两条直线一定是平行线。( )
8. 下面有两条平行线,请你照着图中的样子再画3条垂线段,并量一量它们的长度。
我发现 。
垂直
平行
垂直
×
两条平行线之间的距离处处相等
画图略
题型三
【例3】已知∠1=75°,求∠2,∠3和∠4的度数。
答案:∠2=105°,∠3=75°,∠4=105°。
精析:利用平角是180°以及图中各角之间的关系可以求得∠2=180°-∠1=180°-75°=105°,又根据两直线相交,所形成的对角相等,可得∠1=∠3=75°,∠2=∠4=105°。
举一反三
9. 在直角三角形中,∠B是直角,∠A是∠B的 ,那么∠C是( )。
A. 60° B. 35° C.54°
10. 求右图中∠1,∠2,∠3的度数。
C
∠1=180°-35°=145°
∠2=90°-30°=60°
∠3=90°
题型四
【例4】三角形的一个内角是60度,另外两个内角度数的比是1:5,这个三角形是一个( )三角形。
精析:此题考查的是三角形的分类,可以求得另外两个内角的度数之和是120度,再将120按比分配,求得5份对应的角是100度,可以得出这是一个钝角三角形。
答案:钝角
举一反三
11. 一个等腰三角形,它的顶角的度数是一个底角度数的2倍,它的顶角是( )度,它的一个底角是( )度,如果按角来分,它是一个( )三角形。
90
45
直角
题型五
【例5】已知一个长方体的长、宽、高都是整厘米数,相邻的三个面的面积分别是8平方厘米、6平方厘米和12平方厘米。这个长方体的长、宽、高分别是多少厘米?
精析:把三个面相交的顶点作为基点,相交于这个基点的3条棱分别是长方体的长、宽、高,
然后把每个面的面积转化为3个关系
式:8=长×宽,12=长×高,6=宽×
高。由于长、宽、高都是整厘米数,
可以推算,长是4厘米,宽是2厘米,
高是3厘米。验证:8=4×2,12=4×3,6=2×3。
举一反三
答案:这个长方体的长、宽、高分别是4厘米、2厘米、3厘米。
12. 一个长方体的棱长总和是96厘米,它的长、宽、高的比是5∶4∶3,它的长是( )厘米,宽是( )厘米,高是( )厘米。
13. 一个正方体的棱长总和是120厘米,它的棱长是( )厘米。
10
8
6
10
差错类型及归纳
类型1
对角的含义理解不正确。
【例1】判断:两条射线可以组成一个角。( )
分析:角是由两条有公共端点的射线组成的。本题容易出错的主要原因是对角的概念没有正确理解,还有一个原因是审题不仔细,没有深入思考,看到有两条射线就以为可以组成一个角,而没有考虑到顶点。
正解:×
错解:√
类型2
对钟面问题中的时针、分针、秒针旋转角度关系理解不正确。
【例2】丁丁早上7:25上学,分针刚好转了150°,他就到达学校,他上学用了( )分钟。
错解:45
分析:此题考查的是时间的计算和角的度量的综合运用。因为分针每小时转动360°,所以每分钟转动6°,丁丁从出发到学校的时间内分针转了150°,列式可得150°÷6°=25。
正解:25
针对性练习
一、判断题。(正确的在后面画“√”,错误的画“×”)
1. 角的两条边越长,角就越大。( )
2. 三点半时,时针和分针成直角。( )
×
×
二、填一填。
1. 指针从2的位置,顺时针方向转到5的位置,指针转了( )度。
90
2. 钟面上( )整,时针和分针的夹角是180度。
6时
小考复习训练
一、选择题。
1. 两条平行线间的( )处处相等。
A. 射线 B. 距离 C. 直线
2. 把一个活动的长方形框架拉成平行四边形,那么它的
( )不变, ( ) 变了。
A.面积 B.周长 C.周长和面积
3. 只有一组对边平行,且两个角是直角的四边形是( )。
A. 梯形 B. 平行四边形 C. 长方形 D. 直角梯形
B
D
B
A
4. 6时15分时,钟面上分针与时针所组成的角是( )。
A. 钝角 B. 直角 C. 锐角
5. 用一个4倍的放大镜看一个10°的角,这个角是( )。
A. 10°B. 20°C. 40°
A
A
6. 圆的半径和直径都是一条( ),圆的对称轴是一条( )。
A.射线 B.线段 C.曲线 D.直线
B
D
二、判断题。
1. 一条射线长8米。( )
2. 两条直线相交组成的4个角中如果有一个角是直角,那么其他3个角也是直角。( )
3. 射线是直线的一部分,所以任何一条射线都比直线短。( )
4. 大于90°的角是钝角。( )
×
√
×
×
5.锐角小于直角,所以两个锐角和一定小于直角。( )
6. 任意两个等底等高的梯形可以拼成一个平行四边形。 ( )
7. 用三条长度分别是4厘米、4厘米、8厘米的线段,可以围成一个等腰三角形。( )
×
×
×
三、填空题。
1. ( )直角=( )平角= ( ) 周角=四边形的内
角的和。
2. 如果一个三角形最小的内角大于45度,那么这个三角形是( )三角形。
3. 从直线外一点到这条直线可以画( )条线段。其中( )最短。
4. 延长线段的一端可以得到一条( )。
4
2
1
垂线段
无数
射线
锐角
5. 下图中有( )条线段,( )条射线,( )条直线。
7. 过一点可以画( )直线,过两点可以画( )条直线。
无数条
1
6
8
1
6. 上午9时,时针和分针成( )角,8时成( )角。从10:00至11:00,分针转动的角度是( )度。从7时55分到8时30分,分针旋转了( )度。
直
钝
360
210
8. 等腰三角形的一个底角是32°,它的顶角( )。
116°
9.只有一组对边平行的四边形是( )。
10.用6厘米、9厘米和( )厘米长的三根小棒,可以围成一个三角形。(答案不唯一)
梯形
6
四、作图题。
1. 用量角器量出下面各角的度数,并指出各角之间的关系。
2. 过直线外一点画这条直线的垂线和平行线。
略
略
3. 如下图,从A,B两村各挖一条水渠与河相通,要使水渠最短,应怎样挖 请在图中画出来。
略
五、解决问题。
1. 已知右图∠1=48°,列算式求出∠2,∠3,∠4,∠5的度数。
∠2=90°-∠1=90°-48°=42°
∠3=180°-∠2=180°-42°=138°
∠4=∠2=42°
∠5=90°
2. 如右图所示,AB是一条街道,要从点P修一条小路通向街道AB,怎么修最省工省料?(用线段在图上画出这条线路)如果这幅图的比例尺是1∶20000,这条小路实际是多少米?(测量时取整厘米)
做图略。
①作点P到街道AB的垂线,按这条垂线修路最省工省料。
②量得点P到街道AB的垂线段的长度为1.2厘米,根据比例
尺,计算实际距离为:
1.2÷ =24000(厘米)=240(米)
答:作点P到街道AB的垂线,按这条垂线修路最省工省料,这条小路实际是240米。
第五章 图形与几何
第一课时 图形的认识
知识要点梳理
1.线与角
(1)直线、射线和线段
(2)垂直与平行
①垂直:两条直线相交成直角时,这两条直线互相垂直。其中一条直线叫做另一条直线的垂线,这两条直线的交点叫做垂足。
②平行线:在同一平面内,不相交的两条直线叫做平行线。平行线之间的距离处处相等。
③点到直线的距离:从直线外一点到这条直线所画的垂直线段的长,叫做这个点到直线的距离。
④同一平面内的两条直线不是平行就是相交(垂直是相交的特例)。
(3)垂线的基本性质
①过直线上或直线外一点,有且只有一条直线和已知直线垂直。
②从直线外一点到这条直线上各点所连的线段中,垂线段最短。
2. 角
(1)角的意义:从一点引出的两条射线所组成的图形叫做角。角的大小与两边的长短无关,与两边叉开的大小有关。
(2)角的分类
二、平面图形
1. 三角形
(1)三角形的定义:由3条线段围成的图形(每相邻两条线段的端点相连)叫做三角形。
(2)三角形有三条边、三个顶点、三个角。
(3)从三角形的一个顶点到它的对边作一条垂线,顶点和垂足之间的线段叫做三角形的高,这条对边叫做三角形的底。三角形有3条高。
(4)三角形的分类
①按角分
(5)等边三角形是特殊的等腰三角形,
它们的关系如右图所示。
(6)三角形的特殊性质:三角形具有
稳定性。
(7)三角形的内角和是180°。
(8)三角形任意两条边的和大于第三
边。
2. 四边形
3. 圆
(1)圆的认识:平面上的一种曲线图形。圆中心的一点叫
做圆心,一般用字母O表示。
①半径:连接圆心和圆上任意一点的线段叫做半径,一般用r表示。
②在同一个圆里,有无数条半径,每条半径的长度都相等。
③通过圆心并且两端都在圆上的线段叫做直径,一般用d表示。
④同一个圆里有无数条直径,所有的直径都相等。
⑤同一个圆里,直径等于半径长度的两倍,即d=2r,或
r= 。
⑥圆心决定圆的位置,半径决定圆的大小。直径是圆中最长的线段。
⑦圆有无数条对称轴。
4. 扇形
(1)扇形的定义:一条弧和经过这条弧两端的两条半径所围成的图形叫做扇形。
(2)圆上AB两点之间的部分叫做弧,读作“弧AB”,记作“AB”。
(3)顶点在圆心的角叫做圆心角。
(4)在同一个圆中,扇形的大小与这个扇形的圆心角的大小有关。以半圆为弧的扇形的圆心角是180度,以1/4圆为弧的扇形的圆心角是90度。
(5)扇形有1条对称轴。
三、立体图形
1. 长方体和正方体
(1)顶点:棱和棱的交点。 棱:面和面相交的线段。 相交于一个顶点的三条棱的长度分别叫做长方体的长、宽、高。 把长方体放在桌面上,最多只能看到三个面。
(2)正方体是长、宽、高都相等的长方体,是特殊的长方体。
(3)长方体和正方体的关系:
2. 圆柱和圆锥
典例精析及训练
【例1】画一画。
(1)过N点作AB的垂线。 (2)过P点作AB的平行线。
(3)画出下面各图AB边上的高。
题型一
精析:画垂线、平行线和作图形的高都是必须掌握的技能。(1)用一把三角尺就可以画已知直线的垂线。方法:使三角尺的直角边与已知直线重合,沿重合的直线平移三角尺,使三角尺的另一条直角边和N点重合,过N点沿直角边向已知直线画直线即可。(2)用三角尺平移可以画出已知直线的平行线。方法:把三角尺的一条直角边与已知直线重合,用直尺紧靠三角尺的另一条直角边,沿直尺平移三角尺,原来与已知直线重合的直角边与已知点重合,过点沿三角尺的直角边画直线即可。(3)在作图形的高时,注意垂足应落在AB边上,高一般用虚线来表示,要标出垂足。根据画垂线的方法,用三角板的直角边作图,既快又准确。
答案:(1)
(2)
(3)
举一反三
1. 从直线外一点到这条直线可以画无数条线段,其中最短的是和这条直线( )的线段。
2. 在同一个平面内画已知直线的垂线,可以画( )条,如果过一点画已知直线的垂线,则只能画( )条。
3. 过P点画出直线AB的平行线和垂线。
垂直
无数
1
略
4. 路线设计。
(1)请你画一条从实验室到教学楼最近的路。
(2)请你画一条从实验室到操场最近的路。
略
题型二
【例2】直线a,b,c在同一平面内,a与b互相垂直,b与c互相垂直,那么a与c( )。
A. 垂直 B. 平行 C.平行或垂直
精析:此例题主要考查两直线在同一平面内的位置关系。根据之前所学,我们知道,在同一平面内,两直线的位置关系是相交或平行。本题中,三条直线在同一平面内,因为a与b互相垂直,b与c互相垂直,根据垂直于同一条直线的两直线平行,则可以判断a与c互相平行。因此应该选择答案B。
答案:B
举一反三
5. 长方形相邻的两条边互相( ),相对的两条边互相( )。
6. 两条直线相交成直角时,这两条直线就( )。
7. 判断:不相交的两条直线一定是平行线。( )
8. 下面有两条平行线,请你照着图中的样子再画3条垂线段,并量一量它们的长度。
我发现 。
垂直
平行
垂直
×
两条平行线之间的距离处处相等
画图略
题型三
【例3】已知∠1=75°,求∠2,∠3和∠4的度数。
答案:∠2=105°,∠3=75°,∠4=105°。
精析:利用平角是180°以及图中各角之间的关系可以求得∠2=180°-∠1=180°-75°=105°,又根据两直线相交,所形成的对角相等,可得∠1=∠3=75°,∠2=∠4=105°。
举一反三
9. 在直角三角形中,∠B是直角,∠A是∠B的 ,那么∠C是( )。
A. 60° B. 35° C.54°
10. 求右图中∠1,∠2,∠3的度数。
C
∠1=180°-35°=145°
∠2=90°-30°=60°
∠3=90°
题型四
【例4】三角形的一个内角是60度,另外两个内角度数的比是1:5,这个三角形是一个( )三角形。
精析:此题考查的是三角形的分类,可以求得另外两个内角的度数之和是120度,再将120按比分配,求得5份对应的角是100度,可以得出这是一个钝角三角形。
答案:钝角
举一反三
11. 一个等腰三角形,它的顶角的度数是一个底角度数的2倍,它的顶角是( )度,它的一个底角是( )度,如果按角来分,它是一个( )三角形。
90
45
直角
题型五
【例5】已知一个长方体的长、宽、高都是整厘米数,相邻的三个面的面积分别是8平方厘米、6平方厘米和12平方厘米。这个长方体的长、宽、高分别是多少厘米?
精析:把三个面相交的顶点作为基点,相交于这个基点的3条棱分别是长方体的长、宽、高,
然后把每个面的面积转化为3个关系
式:8=长×宽,12=长×高,6=宽×
高。由于长、宽、高都是整厘米数,
可以推算,长是4厘米,宽是2厘米,
高是3厘米。验证:8=4×2,12=4×3,6=2×3。
举一反三
答案:这个长方体的长、宽、高分别是4厘米、2厘米、3厘米。
12. 一个长方体的棱长总和是96厘米,它的长、宽、高的比是5∶4∶3,它的长是( )厘米,宽是( )厘米,高是( )厘米。
13. 一个正方体的棱长总和是120厘米,它的棱长是( )厘米。
10
8
6
10
差错类型及归纳
类型1
对角的含义理解不正确。
【例1】判断:两条射线可以组成一个角。( )
分析:角是由两条有公共端点的射线组成的。本题容易出错的主要原因是对角的概念没有正确理解,还有一个原因是审题不仔细,没有深入思考,看到有两条射线就以为可以组成一个角,而没有考虑到顶点。
正解:×
错解:√
类型2
对钟面问题中的时针、分针、秒针旋转角度关系理解不正确。
【例2】丁丁早上7:25上学,分针刚好转了150°,他就到达学校,他上学用了( )分钟。
错解:45
分析:此题考查的是时间的计算和角的度量的综合运用。因为分针每小时转动360°,所以每分钟转动6°,丁丁从出发到学校的时间内分针转了150°,列式可得150°÷6°=25。
正解:25
针对性练习
一、判断题。(正确的在后面画“√”,错误的画“×”)
1. 角的两条边越长,角就越大。( )
2. 三点半时,时针和分针成直角。( )
×
×
二、填一填。
1. 指针从2的位置,顺时针方向转到5的位置,指针转了( )度。
90
2. 钟面上( )整,时针和分针的夹角是180度。
6时
小考复习训练
一、选择题。
1. 两条平行线间的( )处处相等。
A. 射线 B. 距离 C. 直线
2. 把一个活动的长方形框架拉成平行四边形,那么它的
( )不变, ( ) 变了。
A.面积 B.周长 C.周长和面积
3. 只有一组对边平行,且两个角是直角的四边形是( )。
A. 梯形 B. 平行四边形 C. 长方形 D. 直角梯形
B
D
B
A
4. 6时15分时,钟面上分针与时针所组成的角是( )。
A. 钝角 B. 直角 C. 锐角
5. 用一个4倍的放大镜看一个10°的角,这个角是( )。
A. 10°B. 20°C. 40°
A
A
6. 圆的半径和直径都是一条( ),圆的对称轴是一条( )。
A.射线 B.线段 C.曲线 D.直线
B
D
二、判断题。
1. 一条射线长8米。( )
2. 两条直线相交组成的4个角中如果有一个角是直角,那么其他3个角也是直角。( )
3. 射线是直线的一部分,所以任何一条射线都比直线短。( )
4. 大于90°的角是钝角。( )
×
√
×
×
5.锐角小于直角,所以两个锐角和一定小于直角。( )
6. 任意两个等底等高的梯形可以拼成一个平行四边形。 ( )
7. 用三条长度分别是4厘米、4厘米、8厘米的线段,可以围成一个等腰三角形。( )
×
×
×
三、填空题。
1. ( )直角=( )平角= ( ) 周角=四边形的内
角的和。
2. 如果一个三角形最小的内角大于45度,那么这个三角形是( )三角形。
3. 从直线外一点到这条直线可以画( )条线段。其中( )最短。
4. 延长线段的一端可以得到一条( )。
4
2
1
垂线段
无数
射线
锐角
5. 下图中有( )条线段,( )条射线,( )条直线。
7. 过一点可以画( )直线,过两点可以画( )条直线。
无数条
1
6
8
1
6. 上午9时,时针和分针成( )角,8时成( )角。从10:00至11:00,分针转动的角度是( )度。从7时55分到8时30分,分针旋转了( )度。
直
钝
360
210
8. 等腰三角形的一个底角是32°,它的顶角( )。
116°
9.只有一组对边平行的四边形是( )。
10.用6厘米、9厘米和( )厘米长的三根小棒,可以围成一个三角形。(答案不唯一)
梯形
6
四、作图题。
1. 用量角器量出下面各角的度数,并指出各角之间的关系。
2. 过直线外一点画这条直线的垂线和平行线。
略
略
3. 如下图,从A,B两村各挖一条水渠与河相通,要使水渠最短,应怎样挖 请在图中画出来。
略
五、解决问题。
1. 已知右图∠1=48°,列算式求出∠2,∠3,∠4,∠5的度数。
∠2=90°-∠1=90°-48°=42°
∠3=180°-∠2=180°-42°=138°
∠4=∠2=42°
∠5=90°
2. 如右图所示,AB是一条街道,要从点P修一条小路通向街道AB,怎么修最省工省料?(用线段在图上画出这条线路)如果这幅图的比例尺是1∶20000,这条小路实际是多少米?(测量时取整厘米)
做图略。
①作点P到街道AB的垂线,按这条垂线修路最省工省料。
②量得点P到街道AB的垂线段的长度为1.2厘米,根据比例
尺,计算实际距离为:
1.2÷ =24000(厘米)=240(米)
答:作点P到街道AB的垂线,按这条垂线修路最省工省料,这条小路实际是240米。
同课章节目录
