六年级下册数学毕业总复习课件-第七章解决实际问题第四课时 人教新课标(共33张PPT)
文档属性
| 名称 | 六年级下册数学毕业总复习课件-第七章解决实际问题第四课时 人教新课标(共33张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 480.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-09 10:16:09 | ||
图片预览











文档简介
(共33张PPT)
第四课时 比和比例应用题
知识要点梳理
1. 比例尺应用题
(1)图上距离∶实际距离=比例尺或
=比例尺
(2)图上距离÷比例尺=实际距离
(3)实际距离×比例尺=图上距离
2. 按比例分配应用题把一个数量按照一定的比进行分配的问题叫做按比例分配问题。解决按比分配的问题,主要有三种方法:一是把比的前项、后项看作分得的份数,先求出每一份,即把此问题转化为整数的“归一问题”来解决;二是求出前项、后项分别占总数的几分之几,即把问题转化为求一个数的几分之几是多少,用分数乘法解答;三是用比例知识来解答。
3. 正、反比例应用题
(1)比例应用题分正比例应用题和反比例应用题。用正比例解答的问题,即关系式为 =k(一定);用反比例解答的问题,即关系式为xy=k(一定)。
(2)解题关键:正确判断正、反比例是解答比例应用题的关键。
(3)解题步骤:
①分析数量关系,判断成什么比例
②找等量关系:若成正比例关系,则按“等比”找等量关系;若成反比例关系,则按“等积”
找等量关系
③ 列比例式:设未知数,并代入等量关系式,得正比例式或反比例式
④解比例
⑤检验并写出答语
典例精析及训练
题型一
【例1】李师傅加工一批零件,原计划每小时加工30个,需12小时完成。实际工作时,李师傅2.5小时就加工了100个,照这样的速度可比原计划提前几小时完成?
精析:题目中“照这样的速度”是指工作效率一定,那么工作时间和工作总量这两个相关联的量成正比例,可列比例式解答。
答案:设照这样的速度可比原计划提前x小时完成。
(30×12)∶(12-x)=100∶2.5
1200-100x=900
100x=1200-900
x=3
答:照这样的速度可比原计划提前3小时完成。
举一反三
1. 一间教室用边长均为0.4米的正方形砖铺地,需要300块。如果改用边长为0.5米的正方形砖铺地需要多少块?
解:设如果改用边长为0.5米的正方形砖铺地需要x块。
(0.4×0.4)∶(0.5×0.5)=x∶300
x=192
答:如果改用边长为0.5米的正方形砖铺地需要192块。
2. 书架里有《小文学》25本,《作文笑传》21本。增加多少本《小文学》,可使书架上《小文学》与《作文笑传》的本数比是9∶7?
解:设增加x本《小文学》。
(25+x)∶21=9∶7
x=2
答:增加2本《小文学》,可使书架上《小学》与《作文笑传》的本数比是9∶7。
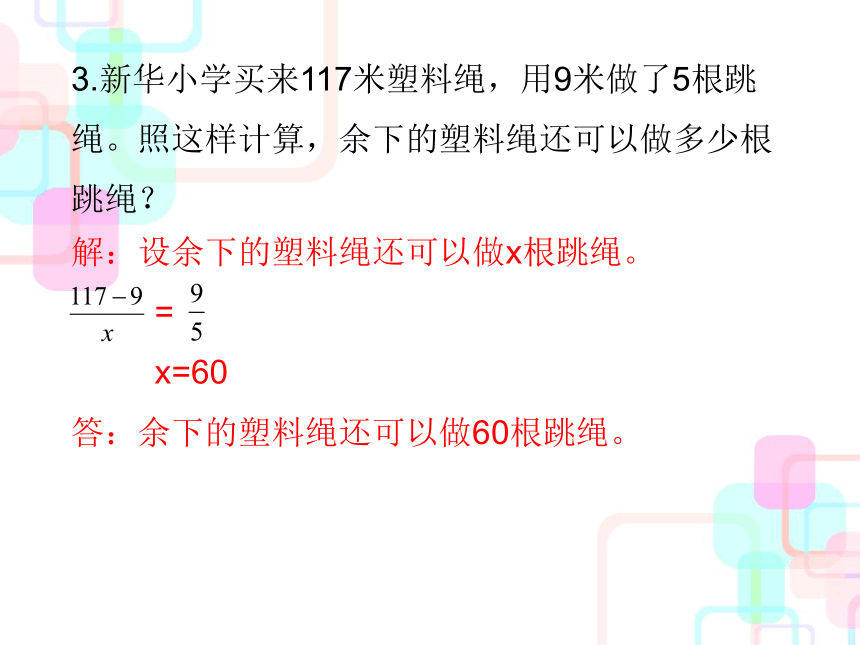
3.新华小学买来117米塑料绳,用9米做了5根跳绳。照这样计算,余下的塑料绳还可以做多少根跳绳?
解:设余下的塑料绳还可以做x根跳绳。
=
x=60
答:余下的塑料绳还可以做60根跳绳。
题型二
【例2】甲、乙两个长方形的周长相等,甲长方形长与宽的比是3∶2,乙长方形的长与宽的比是7∶5,那么甲、乙两个长方形面积的比是多少?
精析:本题灵活性强,无现成模式可套用,主要考查学生学习了“比和比例”这部分知识后,能否灵活运用所学知识解决有一定难度的实际问题。解答的突破口是把长方形的周长具体化。两个长方形的周长相等,周长的一半也相等,甲、乙份数不相等,甲有2+3=5份,乙有5+7=12份,若使它们的周长数的一半等于份数的最小公倍数,可以分别求出两个长方形的长和宽,进一步求出面积,从而求出面积的比。
答案:假设两个长方形周长的一半均为60。
3+2=5 7+5=12
甲长方形的长是60× =36,宽是60-36=24,面积是36×24=864
乙长方形的长是60× =35,宽是60-35=25,面积是35×25=875
甲、乙两个长方形面积的比是 864∶875
答:甲、乙两个长方形面积的比是 864∶875。
5
3
—
12
7
—
举一反三
4. 一种农药,用药液和水按照1∶1500配制而成。如果现只有3千克的药液,能配制这种农药多少千克?
3÷ =4500(千克)
4500+3=4503(千克)
答:能配制这种农药4503千克。
5.一个工程队修筑一段铁路,6个人一个月完成了总工程的 。照这样计算,一个人完成全部工程需要几个月?(用比例解)
解:设一个人完成全部工程需要x个月。
1∶x= ∶6
x=24
答:一个人完成全部工程需要24个月。
题型三
【例3】在比例尺是1∶5000000的地图上量得两个城市相距4.5厘米,一辆客车和一辆货车同时从两个城市相对开出, 小时相遇。火车速度和客车速度的比是9∶11,求客车平均每小时行驶多少千米。
答案:4.5×5000000=22500000厘米=225千米
225÷ =90(千米/时)
90× =49.5(千米/时)
答:客车平均每小时行驶49.5千米。
精析:题中已知比例尺和图上距离,可以根据比例尺的实际意义,求出两个城市之间的实际距离;然后求出两车的速度和;再根据按比例分配的解题思路求出客车的速度。
举一反三
6. 在一幅地图上,量得南京到北京的距离是15厘米,南京到北京的实际距离是900千米,求这幅地图的比例尺。
900千米=90000000厘米
15∶90000000=1∶6000000
答:这幅地图的比例尺是1∶6000000。
7. 在比例尺是1∶6000000的铁路运行图上,量得甲、乙两城间的铁路线长7.2厘米。一列客车从甲城开往乙城用了4.5小时,这列客车平均每小时行驶多少千米?
7.2÷ =43200000(厘米)=432千米
432÷4.5=96(千米)
答:这列客车平均每小时行驶96千米。
8.在比例尺是1∶500的图纸上,量得一个正方形花坛的边长是4厘米。这个花坛的实际面积是多少平方米?
4÷ =2000(厘米)=20(米)
20×20=400(平方米)
答:这个花坛的实际面积是400平方米。
差错类型及归纳
类型1
锯木头的问题,锯的段数和锯的下数概念分不清楚。
【例】一根木料,锯3段需要9分钟,如果照这样的速度锯6段需要多少分钟?(用比例解)
错解:设需要x分钟。
=
3x=9×6
x=18
答:需要18分钟。
分析:此题错在认为锯的时间与锯的段数成正比例,其实是锯一下的时间一定,也就是锯的时间与锯的下数成正比例。
正解:设需要x分钟。
=
2x=9×5
x=22.5
答:需要22.5分钟。
针对性练习
一、40千克小麦能磨面粉32千克,照这样计算,7吨小麦能磨面粉多少千克?(用比例解)
解:设7吨小麦能磨面粉x千克。
32∶40=x∶7000
x=5600
答:7吨小麦能磨面粉5600千克。
二、下表是一根木料锯成的段数与锯的次数之间的关系的分析表。
1.请你根据实际生活经验完成下表。
2.若将一根木料锯成5段要8分钟,那么将它锯成6段需要多少分钟?请列式计算。
解:设锯成6段需要x分钟。
= x=10
答:锯成6段需要10分钟。
1
2
3
4
1=2-1
2=3-1
3=4-1
4=5-1
小考复习训练
用比例知识解答下面的应用题。
1.北京与杭州相距1250千米,在比例尺是1∶25000000的中国地图上,量得这两地之间的距离是多少厘米?
1250千米=125000000厘米
125000000× =5(厘米)
答:量得这两地之间的距离是5厘米。
2. 在比例尺是1∶400的学校操场平面图上,量得操场长15厘米,宽6.5厘米,这个操场的实际占地面积是多少平方米?
15÷ =6000(厘米)=60(米)
6.5÷ =2600(厘米)=26(米)
60×26=1560(平方米)
答:这个操场的实际占地面积是1560平方米。
3.某种型号的钢珠,3个重22.5克。现有一批这种型号的钢珠,共重945克,这批钢珠一共有多少个?
解:设这批钢珠一共有x个。
22.5∶3=945:x
x=126
答:这批钢珠一共有126个。
4.一个晒盐场用500千克海水可以晒15千克盐。照这样计算,用100吨海水可以晒多少吨盐?(用比例方法解答)
解:设用100吨海水可以晒x吨盐。
15∶500=x∶100
x=3
答:用100吨海水可以晒3吨盐。
5. 修一段长1500米的公路,已修了这段公路的 ,剩下的按7∶3分给甲、乙两个修路队来修,求乙修路队要修多少米?
1500× =1000(米)
1000× =300(米)
答:乙修路队要修300米。
6.右图是一个梯形地平面图(单位:厘米),求它的实际面积。
上底:3×200=600(厘米)=6(米)
下底:5×200=1000(厘米)=10(米)
高:4×200=800(厘米)=8(米)
(6+10)×8÷2=64(平方米)
答:它的实际面积为64平方米。
7. 同学们做操,每行站20人,正好站18行。如果每行站24人,可以站多少行?(用比例方法解)
解:设可以站x行。
24x=20×18
x=15
答:可以站15行。
8. 在一副地图上量得A,B两城之间的距离是6厘米,而实际距离是840千米。如果C,D两城之间的实际距离是560千米,在地图上量得C,D两城之间的距离是多少厘米?
解:设在地图上量得C,D两城之间的距离是x厘米。
x=4
答:在地图上量得C,D两城之间的距离是4厘米。
9.园林绿化队要栽一批树苗,第一天栽了总数的 ,第二天栽了130棵,这时已栽的与剩下的棵数的比是3∶5。这批树苗一共有多少棵?
解:设这批树苗一共有x棵。
( x+130)∶x=3∶(3+5)
x=1200
答:这批树苗一共有1200棵。
15
4
__
10.用一种方砖铺一间长12米,宽8米的实验室地面。先用400块方砖铺设了64平方米,余下的还要用这种砖多少块?
解:设余下的还要用这种砖x块。
12×8=96(平方米)
=
x=200
答:余下的还要用这种砖200块。
64
400
___
96-64
x
____
第四课时 比和比例应用题
知识要点梳理
1. 比例尺应用题
(1)图上距离∶实际距离=比例尺或
=比例尺
(2)图上距离÷比例尺=实际距离
(3)实际距离×比例尺=图上距离
2. 按比例分配应用题把一个数量按照一定的比进行分配的问题叫做按比例分配问题。解决按比分配的问题,主要有三种方法:一是把比的前项、后项看作分得的份数,先求出每一份,即把此问题转化为整数的“归一问题”来解决;二是求出前项、后项分别占总数的几分之几,即把问题转化为求一个数的几分之几是多少,用分数乘法解答;三是用比例知识来解答。
3. 正、反比例应用题
(1)比例应用题分正比例应用题和反比例应用题。用正比例解答的问题,即关系式为 =k(一定);用反比例解答的问题,即关系式为xy=k(一定)。
(2)解题关键:正确判断正、反比例是解答比例应用题的关键。
(3)解题步骤:
①分析数量关系,判断成什么比例
②找等量关系:若成正比例关系,则按“等比”找等量关系;若成反比例关系,则按“等积”
找等量关系
③ 列比例式:设未知数,并代入等量关系式,得正比例式或反比例式
④解比例
⑤检验并写出答语
典例精析及训练
题型一
【例1】李师傅加工一批零件,原计划每小时加工30个,需12小时完成。实际工作时,李师傅2.5小时就加工了100个,照这样的速度可比原计划提前几小时完成?
精析:题目中“照这样的速度”是指工作效率一定,那么工作时间和工作总量这两个相关联的量成正比例,可列比例式解答。
答案:设照这样的速度可比原计划提前x小时完成。
(30×12)∶(12-x)=100∶2.5
1200-100x=900
100x=1200-900
x=3
答:照这样的速度可比原计划提前3小时完成。
举一反三
1. 一间教室用边长均为0.4米的正方形砖铺地,需要300块。如果改用边长为0.5米的正方形砖铺地需要多少块?
解:设如果改用边长为0.5米的正方形砖铺地需要x块。
(0.4×0.4)∶(0.5×0.5)=x∶300
x=192
答:如果改用边长为0.5米的正方形砖铺地需要192块。
2. 书架里有《小文学》25本,《作文笑传》21本。增加多少本《小文学》,可使书架上《小文学》与《作文笑传》的本数比是9∶7?
解:设增加x本《小文学》。
(25+x)∶21=9∶7
x=2
答:增加2本《小文学》,可使书架上《小学》与《作文笑传》的本数比是9∶7。
3.新华小学买来117米塑料绳,用9米做了5根跳绳。照这样计算,余下的塑料绳还可以做多少根跳绳?
解:设余下的塑料绳还可以做x根跳绳。
=
x=60
答:余下的塑料绳还可以做60根跳绳。
题型二
【例2】甲、乙两个长方形的周长相等,甲长方形长与宽的比是3∶2,乙长方形的长与宽的比是7∶5,那么甲、乙两个长方形面积的比是多少?
精析:本题灵活性强,无现成模式可套用,主要考查学生学习了“比和比例”这部分知识后,能否灵活运用所学知识解决有一定难度的实际问题。解答的突破口是把长方形的周长具体化。两个长方形的周长相等,周长的一半也相等,甲、乙份数不相等,甲有2+3=5份,乙有5+7=12份,若使它们的周长数的一半等于份数的最小公倍数,可以分别求出两个长方形的长和宽,进一步求出面积,从而求出面积的比。
答案:假设两个长方形周长的一半均为60。
3+2=5 7+5=12
甲长方形的长是60× =36,宽是60-36=24,面积是36×24=864
乙长方形的长是60× =35,宽是60-35=25,面积是35×25=875
甲、乙两个长方形面积的比是 864∶875
答:甲、乙两个长方形面积的比是 864∶875。
5
3
—
12
7
—
举一反三
4. 一种农药,用药液和水按照1∶1500配制而成。如果现只有3千克的药液,能配制这种农药多少千克?
3÷ =4500(千克)
4500+3=4503(千克)
答:能配制这种农药4503千克。
5.一个工程队修筑一段铁路,6个人一个月完成了总工程的 。照这样计算,一个人完成全部工程需要几个月?(用比例解)
解:设一个人完成全部工程需要x个月。
1∶x= ∶6
x=24
答:一个人完成全部工程需要24个月。
题型三
【例3】在比例尺是1∶5000000的地图上量得两个城市相距4.5厘米,一辆客车和一辆货车同时从两个城市相对开出, 小时相遇。火车速度和客车速度的比是9∶11,求客车平均每小时行驶多少千米。
答案:4.5×5000000=22500000厘米=225千米
225÷ =90(千米/时)
90× =49.5(千米/时)
答:客车平均每小时行驶49.5千米。
精析:题中已知比例尺和图上距离,可以根据比例尺的实际意义,求出两个城市之间的实际距离;然后求出两车的速度和;再根据按比例分配的解题思路求出客车的速度。
举一反三
6. 在一幅地图上,量得南京到北京的距离是15厘米,南京到北京的实际距离是900千米,求这幅地图的比例尺。
900千米=90000000厘米
15∶90000000=1∶6000000
答:这幅地图的比例尺是1∶6000000。
7. 在比例尺是1∶6000000的铁路运行图上,量得甲、乙两城间的铁路线长7.2厘米。一列客车从甲城开往乙城用了4.5小时,这列客车平均每小时行驶多少千米?
7.2÷ =43200000(厘米)=432千米
432÷4.5=96(千米)
答:这列客车平均每小时行驶96千米。
8.在比例尺是1∶500的图纸上,量得一个正方形花坛的边长是4厘米。这个花坛的实际面积是多少平方米?
4÷ =2000(厘米)=20(米)
20×20=400(平方米)
答:这个花坛的实际面积是400平方米。
差错类型及归纳
类型1
锯木头的问题,锯的段数和锯的下数概念分不清楚。
【例】一根木料,锯3段需要9分钟,如果照这样的速度锯6段需要多少分钟?(用比例解)
错解:设需要x分钟。
=
3x=9×6
x=18
答:需要18分钟。
分析:此题错在认为锯的时间与锯的段数成正比例,其实是锯一下的时间一定,也就是锯的时间与锯的下数成正比例。
正解:设需要x分钟。
=
2x=9×5
x=22.5
答:需要22.5分钟。
针对性练习
一、40千克小麦能磨面粉32千克,照这样计算,7吨小麦能磨面粉多少千克?(用比例解)
解:设7吨小麦能磨面粉x千克。
32∶40=x∶7000
x=5600
答:7吨小麦能磨面粉5600千克。
二、下表是一根木料锯成的段数与锯的次数之间的关系的分析表。
1.请你根据实际生活经验完成下表。
2.若将一根木料锯成5段要8分钟,那么将它锯成6段需要多少分钟?请列式计算。
解:设锯成6段需要x分钟。
= x=10
答:锯成6段需要10分钟。
1
2
3
4
1=2-1
2=3-1
3=4-1
4=5-1
小考复习训练
用比例知识解答下面的应用题。
1.北京与杭州相距1250千米,在比例尺是1∶25000000的中国地图上,量得这两地之间的距离是多少厘米?
1250千米=125000000厘米
125000000× =5(厘米)
答:量得这两地之间的距离是5厘米。
2. 在比例尺是1∶400的学校操场平面图上,量得操场长15厘米,宽6.5厘米,这个操场的实际占地面积是多少平方米?
15÷ =6000(厘米)=60(米)
6.5÷ =2600(厘米)=26(米)
60×26=1560(平方米)
答:这个操场的实际占地面积是1560平方米。
3.某种型号的钢珠,3个重22.5克。现有一批这种型号的钢珠,共重945克,这批钢珠一共有多少个?
解:设这批钢珠一共有x个。
22.5∶3=945:x
x=126
答:这批钢珠一共有126个。
4.一个晒盐场用500千克海水可以晒15千克盐。照这样计算,用100吨海水可以晒多少吨盐?(用比例方法解答)
解:设用100吨海水可以晒x吨盐。
15∶500=x∶100
x=3
答:用100吨海水可以晒3吨盐。
5. 修一段长1500米的公路,已修了这段公路的 ,剩下的按7∶3分给甲、乙两个修路队来修,求乙修路队要修多少米?
1500× =1000(米)
1000× =300(米)
答:乙修路队要修300米。
6.右图是一个梯形地平面图(单位:厘米),求它的实际面积。
上底:3×200=600(厘米)=6(米)
下底:5×200=1000(厘米)=10(米)
高:4×200=800(厘米)=8(米)
(6+10)×8÷2=64(平方米)
答:它的实际面积为64平方米。
7. 同学们做操,每行站20人,正好站18行。如果每行站24人,可以站多少行?(用比例方法解)
解:设可以站x行。
24x=20×18
x=15
答:可以站15行。
8. 在一副地图上量得A,B两城之间的距离是6厘米,而实际距离是840千米。如果C,D两城之间的实际距离是560千米,在地图上量得C,D两城之间的距离是多少厘米?
解:设在地图上量得C,D两城之间的距离是x厘米。
x=4
答:在地图上量得C,D两城之间的距离是4厘米。
9.园林绿化队要栽一批树苗,第一天栽了总数的 ,第二天栽了130棵,这时已栽的与剩下的棵数的比是3∶5。这批树苗一共有多少棵?
解:设这批树苗一共有x棵。
( x+130)∶x=3∶(3+5)
x=1200
答:这批树苗一共有1200棵。
15
4
__
10.用一种方砖铺一间长12米,宽8米的实验室地面。先用400块方砖铺设了64平方米,余下的还要用这种砖多少块?
解:设余下的还要用这种砖x块。
12×8=96(平方米)
=
x=200
答:余下的还要用这种砖200块。
64
400
___
96-64
x
____
同课章节目录
