【暑期预习】第十一讲 代数式复习 学案(含答案)-苏科版七年级上册
文档属性
| 名称 | 【暑期预习】第十一讲 代数式复习 学案(含答案)-苏科版七年级上册 | 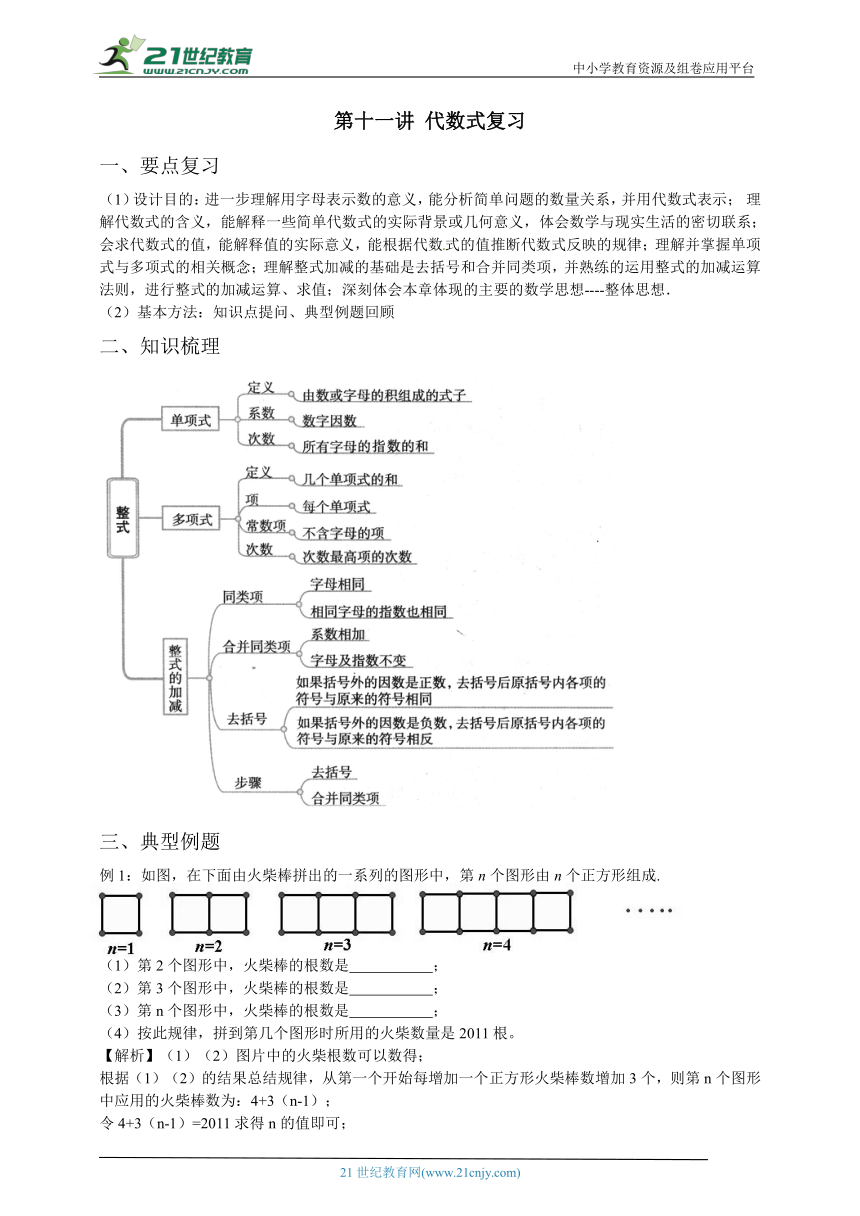 | |
| 格式 | doc | ||
| 文件大小 | 948.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-10 22:15:10 | ||
图片预览





文档简介
中小学教育资源及组卷应用平台
第十一讲 代数式复习
一、要点复习
(1)设计目的:进一步理解用字母表示数的意义,能分析简单问题的数量关系,并用代数式表示; 理解代数式的含义,能解释一些简单代数式的实际背景或几何意义,体会数学与现实生活的密切联系;会求代数式的值,能解释值的实际意义,能根据代数式的值推断代数式反映的规律;理解并掌握单项式与多项式的相关概念;理解整式加减的基础是去括号和合并同类项,并熟练的运用整式的加减运算法则,进行整式的加减运算、求值;深刻体会本章体现的主要的数学思想----整体思想.
(2)基本方法:知识点提问、典型例题回顾
二、知识梳理
三、典型例题
例1:如图,在下面由火柴棒拼出的一系列的图形中,第n个图形由n个正方形组成.
(1)第2个图形中,火柴棒的根数是 ;
(2)第3个图形中,火柴棒的根数是 ;
(3)第n个图形中,火柴棒的根数是 ;
(4)按此规律,拼到第几个图形时所用的火柴数量是2011根。
【解析】(1)(2)图片中的火柴根数可以数得;
根据(1)(2)的结果总结规律,从第一个开始每增加一个正方形火柴棒数增加3个,则第n个图形中应用的火柴棒数为:4+3(n-1);
令4+3(n-1)=2011求得n的值即可;
【解答】解:根据已知图形可以发现:
第2个图形中,火柴棒的根数是7;
第3个图形中,火柴棒的根数是10;
∵每增加一个正方形火柴棒数增加3,
∴第n个图形中应有火柴棒数为:4+3(n-1)=3n+1;
当4+3(n-1)=2011时,解得:n=700,答:第700个图形有火柴棒数量2011根;
故答案为:(1)7;(2)10;(3)3n+1;(4)2011;
例2:在中多项式的个数有 个.
【解析】根据多项式的定义来判定,多个单项式的和是多项式;
【解答】解:因为3mn是乘积的形式,所以它是单项式;
故答案为:4;
变式:(1)多项式中,四次项的系数为 .
(2)若为七次四项式,则= .
【解析】根据多项式的项和次数以及单项式的系数的定义解答即可;
【解答】(1)多项式是由四项组成,所以是四项式;其中四次项的系数是为1;
由于多项式是关于、的七次四项式,所以,解得将代入到=;
故答案为:(1)1;(2)5;
变式:若多项式A与多项式的和为,则多项式A为 .
【解析】根据多项式的加减运算法则对代数式进行计算;
【解答】根据题意可得这个多项式A为:
故答案为:;
例3:若是同类项,则x+y= .
【解析】利用同类项的定义求出的值,即可确定出的值;
【解答】∵
∴
∴将的值代入到中得
故答案为:9;
变式:若与是同类项,求代数式的值.
【解析】利用同类项的定义求出的值,代入代数式求值即可;
【解答】解:∵与是同类项,
∴
∴
又∵=;
将的值代入到
故答案为:15;
例4:化简求值:,其中
【解析】原式去括号合并得到最简结果,把与的值代入计算即可求出值;
【解答】解:原式=
当原式=;
故答案为:;
变式:若,求的值.
【解析】由非负数的性质先求得的值,然后代入数值进行计算即可;
【解答】解:∵∴
=
=
=
故答案为:8;
例5:对于代数式2x2+7xy+3y2+x2-kxy+5y2,老师提出了两个问题,第一个问题是:当k为何值时,代数式中不含xy项,第二个问题是:在第一问的前提下,如果x=2,y=-1,代数式的值是多少?(1)小明同学很快就完成了第一个问题,也请你把你的解答写在下面吧.(2)在做第二个问题时,马小虎同学把y=-1,错看成y=1,可是他得到的最后结果却是正确的,你知道这是为什么吗?
【解析】(1)代数式中不含xy项就是合并同类项以后xy的系数为0,据此可以得出;
(2)把x=2,y=-1和x=2,y=1代入(1)中的代数式求值即可判断;
【解答】解:(1)因为2x2+7xy+3y2+x2-kxy+5y2
=(2x2+x2)+(3y2+5y2)+(7xy-kxy)
=3x2+8y2+(7-k)xy
所以只要7-k=0,这个代数式就不含有xy项,即k=7,代数式中不含有xy项;
(2)因为在第一问的前提下原代数式为3x2+8y2
当x=2,y=-1时,原式=3×22+8×(-1)2=12+8=20;
所以马小虎的结果是正确的;
故答案为:(1)k=7;(2)20;
变式:若已知,则 .
【解析】利用代数式整体代入的方法即可求出值;
【解答】∵;
∴
又∵
∴原式=
故答案为:
例6:一个两位数,十位上数字,个位上数字分别是.已知,现将十位上数字,个位上数字都减去3,所在位置不变组成一个新两位数.求原两位数与新两位数之和是多少
【解析】根据题意列出正确的代数式,然后代数式求和即可;
【解答】由题意知原来的两位数是,现在两个数都减去3,所得的新的两位数为:所以两个数求和所得的结果为:
故答案为:;
四、易错指津
一、选择题
1.单项式2a的系数是( )
A.2 B.2a C.1 D.a
2.下列计算正确的个数 ( ).
① ;② ; ③ ;
④ ; ⑤
A.2 B.1 C.4 D.0
3.现规定一种运算:a * b = ab + a - b,其中a,b为有理数,则3 * 5的值为( ).
A.11 B.12 C.13 D.14
4.化简(n为正整数)的结果为( ).
A.0 B.-2a C.2a D.2a或-2a
5.已知a-b=-3,c+d=2,则(b+c)-(a-d)为( ).
A.-1 B.-5 C.5 D.1
6. 有理数a,b,c在数轴上的位置如右图所示,则 ( ).
A.-2b B.0
C.2c D.2c-2b
7.当x=-3时,多项式的值是7,那么当x=3时,它的值是( ).
A.-3 B.-7 C.7 D.-17
8.如果是关于的二次三项式,那么m,n应满足的条件是( ).
A.m=1,n=5 B.m≠1,n>3
C.m≠-1,n为大于3的整数 D.m≠-1,n=5
五、课堂练习
1.是关于x,y的一个单项式,且系数是3,次数是4,则m=________,n=________.
2. (1)(___________);
(2)2a-3(b-c)=___________.
(3)(________)=7x+8.
3.当b=________时,式子2a+ab-5的值与a无关.
4.若,则________.
5.一台电视机原价是2500元,现按原价的8折出售,则购买a台这样的电视机需要 元.
6.当k=__________时,多项式x2-3kxy-3y2-xy-8中不含xy项.
7.若mn=m+3,则2mn+3m﹣5mn+10= .
8.如图,是用棋子摆成的图案,摆第1个图案需要7枚棋子,摆第2个图案需要19枚棋子,摆第3个图案需要37枚棋子,按照这样的方式摆下去,则摆第6个图案需要 枚棋子,摆第n个图案需要 枚棋子.
9.先化简,再求值.
(a2+1)﹣3a(a﹣1)+2(a2+a﹣1),其中a=﹣1.
10.观察下列一串单项式的特点:xy,﹣2x2y,4x3y,﹣8x4y,16x5y,…
(1)按此规律写出第9个单项式;
(2)试猜想第N个单项式为多少?它的系数和次数分别是多少?
11. 如图所示,用三种大小不同的六个正方形
和一个缺角的正方形拼成长方形ABCD,
其中,GH=2cm, GK=2cm, 设BF=x cm,
(1)用含x的代数式表示CM= cm,
DM= cm.
(2)若x=2cm,求长方形ABCD的面积.
12. 测得一弹簧的长度L(厘米)与悬挂物体的质量x(千克)有下面一组对应值:
试根据表中各对对应值解答下列问题:
(1)用代数式表示挂质量为x千克的物体时的弹簧的长度L.
(2)求所挂物体的质量为10千克时,弹簧的长度是多少?
(3)若测得弹簧的长度是18厘米,则所挂物体的质量为多少千克?
(4)若要求弹簧的长度不超过20厘米,则所挂物体的质量不能超过多少千克?
六、举一反三
一、选择题
1.已知a与b互为相反数,且x与y互为倒数,那么|a+b|-2xy的值为( ).
A.2 B.-2 C.-1 D.无法确定
2.多项式2a2b﹣ab2﹣ab的项数及次数分别是( )
A.3,3 B.3,2 C.2,3 D.2,2
3.在-3,π,-2,,,六个代数式中,是单项式的个数( )
A.2个 B.3个 C.4个 D.5个
4.对于式子,下列说法正确的是( ).
A.不是单项式
B.是单项式,系数为-1.2×10,次数是7
C.是单项式,系数为-1.2×104,次数是3
D.是单项式,系数为-1.2,次数是3
5.下面计算正确的是( )
A.3-=3 B.3+2=5 C.3+=3 D.-0.25+=0
6.2a-(5b-c+3d-e)=2a□5b□c□3d□e,方格内所填的符号依次是( ).
A.+,-,+,- B.-,-,+,-
C.-,+,-,+ D.-,+,-,-
7.某工厂现有工人a人,若现有工人数比两年前减少了35%,则该工厂两年前工人数为( ).
A. B.(1+35%)a C. D.(1-35%)a
8.若的值为8,则的值是( ).
A.2 B.-17 C.-7 D.7
二、填空题
9.端午节期间,“惠民超市”销售的粽子打8折后卖a元,则粽子的原价卖_______元.
10.单项式的系数是 ,次数是 .
11.是________次________项式,最高次项的系数是________.
12.化简:2a-(2a-1)=________.
13.如果,,那么________.
14.一个多项式减去3x等于,则这个多项式为________.
15.若与﹣3ab的和为单项式,则m+n= .
16.如图所示,外圆半径是R厘米,内圆半径是r厘米,四个小圆的半径都是2厘米,则图中阴影部分的面积是________平方厘米.
三、解答题
17.化简:
(1) (2)
18.已知:,,,当时,求代数式的值.
19.列式计算:一个多项式加上2x2﹣x+5等于4x2﹣6x﹣3,求这个多项式?
20.某农场有耕地1000亩,种粮食、棉花和蔬菜. 其中蔬菜用地a亩,粮食用地比蔬菜用地的6倍还多b亩,求棉花用地多少亩?当a=120,b=4时,棉花用地多少亩?
七、拓宽视野
法老问泰勒斯用什么工具来量金字塔。泰勒斯说只用一根木棍和一把尺子,他把木棍插在金字塔旁边,等木棍的影子和木棍一样长的时候,他量了金字塔影子的长度和金字塔底面边长的一半。把这两个长度加起来就是金字塔的高度了。泰勒斯真是世界上最聪明的人,他不用爬到金字塔的顶上就方便量出了金字塔的高度。
第十一讲 代数式的复习
【答案与解析】
四、易错指津
1.【答案】A.
2.【答案】D
3. 【答案】C
【解析】按规定的运算得:3*5=3×5+3-5=13.
4. 【答案】A
【解析】分析两种情况,当n为偶数时,,,当n为奇数时,,,无论哪种情况,结果都是0.
5.【答案】C
【解析】(b+c)-(a-d)=b+c-a+d=-a+b+c+d=-(a-b)+(c+d)
当a-b=-3,c+d=2时,原式=-(-3)+2=5,所以选C.
6.【答案】B
7. 【答案】D
【解析】由已知条件得:,通过适应变形得:
.当x=3时,原式,再把变形后的式子的值整体代入即可.
8.【答案】D
【解析】由题意得:n-3=2且m+1≠0,得n=5且m≠-1.
五、课堂练习
1.【答案】-3 , 3
【解析】由系数为3,得-m=3,则m=-3.由次数为4,得x,y的指数之和为4,即n+1=4,则n=3.
2.【答案】
3.【答案】-2
【解析】2a+ab-5=(2+b)a-5.因为式子的值与a无关,故2+b=0,所以b=-2.
4.【答案】-24
【解析】因为与互为相反数,又因为,
所以,由此可得.
5.【答案】2000a.
6.【答案】-;
【解析】,解得.
7.【答案】1;
【解析】解:原式=﹣3mn+3m+10,
把mn=m+3代入得:原式=﹣3m﹣9+3m+10=1,
故答案为:1.
8.【答案】127, .
【解析】∵第1个图形需要7=1+6×1枚棋子,
第2个比第1个多12个,即1+6×(1+2)枚,
第3个比第2个多18个,即1+6×(1+2+3)枚,
第4个比第三个多24个,即1+6×(1+2+3+4)=61枚,
……,
∴第n个比第(n-1)个多6n个,即1+6×(1+2+3+4+…+n)=3n2+3n+1枚.
9. 【解析】
解:原式=a2+1﹣3a2+3a+2a2+2a﹣2=5a﹣1,
当a=﹣1时,
原式=﹣5﹣1=﹣6.
10.【解析】
解:(1)∵当n=1时,xy,
当n=2时,﹣2x2y,
当n=3时,4x3y,
当n=4时,﹣8x4y,
当n=5时,16x5y,
∴第9个单项式是29﹣1x9y,即256x9y.
(2)∴n为偶数时,单项式为负数.x的指数为n时,2的指数为n﹣1,
∴当n为奇数时的单项式为2n﹣1xny,
它的系数是2n﹣1,次数是n+1.
11.【解析】
解:(1)(x+2),(2x+2)(或(3x)).
(2)长方形的长为: (cm),
宽为:(cm).
∴长方形的面积为:14×10=140 (cm2).
答:长方形ABCD的面积为140cm2 .
12.【解析】
解:(1).
(2)将,代入,得(㎝)
∴所挂物体的质量为10千克时,弹簧的长度是17㎝.
(3)将,代入,得,解得
∴若测得弹簧的长度是18厘米,则所挂物体的质量为12千克.
(4)∵弹簧的长度不超过20厘米,即L≤20,
∴≤20,得≤16.
∴若要求弹簧的长度不超过20厘米,则所挂物体的质量不能超过16千克.
六、举一反三
一、选择题
1. 【答案】B
【解析】根据已知条件,a与b互为相反数,即a+b=0,x与y互为倒数,即xy=1,所以|a+b|-2xy=0-2×1=-2,故选B.
2.【答案】A
【解析】2a2b﹣ab2﹣ab是三次三项式,故次数是3,项数是3.
3. 【答案】B
【解析】解:﹣3,﹣x2y是单项式.注意-2是分式.故选:B.
4.【答案】 C
【解析】此单项式的系数是以科学记数法形式出现的数,所以系数为-1.2×104,次数应为x与y的指数之和,不包括10的指数4,故次数为3.不要犯“见指数就相加”的错误.所以正确答案为C.
5. 【答案】D
6.【答案】 C
【解析】因为括号前是“-”号,所以去括号时,括号里各项都变号,故选C.
7. 【答案】C
【解析】把减少前的工人数看作整体“1”,已知一个数的(1-35%)是a,求这个数,则是,注意列式时不能用“÷”号,要写成分数形式.
8.【答案】C
【解析】,,,故.
二、填空题
9.【答案】.
10. 【答案】;
11.【答案】三, 三 , ;
【解析】多项式的次数取决于次数最高项的次数,确定系数时不要忽视前面的“-”号.
12.【答案】1;
【解析】先根据去括号法则去括号,然后合并同类项即可,2a-(2a-1)=2a-2a+1=1.
13.【答案】5;
【解析】用前式减去后式可得.
14.【答案】;
【解析】要求的多项式实际上是,化简可得出结果.
15.【答案】4;
【解析】解:∵与﹣3ab的和为单项式,
∴2m﹣5=1,n+1=3﹣n,
解得:m=3,n=1.
故m+n=4.
故答案为:4.
16.【答案】;
【解析】阴影部分的面积=大圆面积-最中间的圆的面积-4个小圆的面积.
三、解答题
17. 【解析】
解:(1)
原式==.
(2)
18.【解析】
解:∵ ∴
∴
当时,
.
19.【解析】
解:根据题意得:(4x2﹣6x﹣3)﹣(2x2﹣x+5)=4x2﹣6x﹣3﹣2x2+x﹣5=2x2﹣5x﹣8.
20.【解析】
解:棉花用地:1000-a-(6a+b)=(1000-7a-b)亩.
当a=120,b=4时,原式=1000-7×120-4
=156(亩).
答:棉花用地(1000-7a-b)亩.当a=120,b=4时,棉花用地为156亩.
…
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
第十一讲 代数式复习
一、要点复习
(1)设计目的:进一步理解用字母表示数的意义,能分析简单问题的数量关系,并用代数式表示; 理解代数式的含义,能解释一些简单代数式的实际背景或几何意义,体会数学与现实生活的密切联系;会求代数式的值,能解释值的实际意义,能根据代数式的值推断代数式反映的规律;理解并掌握单项式与多项式的相关概念;理解整式加减的基础是去括号和合并同类项,并熟练的运用整式的加减运算法则,进行整式的加减运算、求值;深刻体会本章体现的主要的数学思想----整体思想.
(2)基本方法:知识点提问、典型例题回顾
二、知识梳理
三、典型例题
例1:如图,在下面由火柴棒拼出的一系列的图形中,第n个图形由n个正方形组成.
(1)第2个图形中,火柴棒的根数是 ;
(2)第3个图形中,火柴棒的根数是 ;
(3)第n个图形中,火柴棒的根数是 ;
(4)按此规律,拼到第几个图形时所用的火柴数量是2011根。
【解析】(1)(2)图片中的火柴根数可以数得;
根据(1)(2)的结果总结规律,从第一个开始每增加一个正方形火柴棒数增加3个,则第n个图形中应用的火柴棒数为:4+3(n-1);
令4+3(n-1)=2011求得n的值即可;
【解答】解:根据已知图形可以发现:
第2个图形中,火柴棒的根数是7;
第3个图形中,火柴棒的根数是10;
∵每增加一个正方形火柴棒数增加3,
∴第n个图形中应有火柴棒数为:4+3(n-1)=3n+1;
当4+3(n-1)=2011时,解得:n=700,答:第700个图形有火柴棒数量2011根;
故答案为:(1)7;(2)10;(3)3n+1;(4)2011;
例2:在中多项式的个数有 个.
【解析】根据多项式的定义来判定,多个单项式的和是多项式;
【解答】解:因为3mn是乘积的形式,所以它是单项式;
故答案为:4;
变式:(1)多项式中,四次项的系数为 .
(2)若为七次四项式,则= .
【解析】根据多项式的项和次数以及单项式的系数的定义解答即可;
【解答】(1)多项式是由四项组成,所以是四项式;其中四次项的系数是为1;
由于多项式是关于、的七次四项式,所以,解得将代入到=;
故答案为:(1)1;(2)5;
变式:若多项式A与多项式的和为,则多项式A为 .
【解析】根据多项式的加减运算法则对代数式进行计算;
【解答】根据题意可得这个多项式A为:
故答案为:;
例3:若是同类项,则x+y= .
【解析】利用同类项的定义求出的值,即可确定出的值;
【解答】∵
∴
∴将的值代入到中得
故答案为:9;
变式:若与是同类项,求代数式的值.
【解析】利用同类项的定义求出的值,代入代数式求值即可;
【解答】解:∵与是同类项,
∴
∴
又∵=;
将的值代入到
故答案为:15;
例4:化简求值:,其中
【解析】原式去括号合并得到最简结果,把与的值代入计算即可求出值;
【解答】解:原式=
当原式=;
故答案为:;
变式:若,求的值.
【解析】由非负数的性质先求得的值,然后代入数值进行计算即可;
【解答】解:∵∴
=
=
=
故答案为:8;
例5:对于代数式2x2+7xy+3y2+x2-kxy+5y2,老师提出了两个问题,第一个问题是:当k为何值时,代数式中不含xy项,第二个问题是:在第一问的前提下,如果x=2,y=-1,代数式的值是多少?(1)小明同学很快就完成了第一个问题,也请你把你的解答写在下面吧.(2)在做第二个问题时,马小虎同学把y=-1,错看成y=1,可是他得到的最后结果却是正确的,你知道这是为什么吗?
【解析】(1)代数式中不含xy项就是合并同类项以后xy的系数为0,据此可以得出;
(2)把x=2,y=-1和x=2,y=1代入(1)中的代数式求值即可判断;
【解答】解:(1)因为2x2+7xy+3y2+x2-kxy+5y2
=(2x2+x2)+(3y2+5y2)+(7xy-kxy)
=3x2+8y2+(7-k)xy
所以只要7-k=0,这个代数式就不含有xy项,即k=7,代数式中不含有xy项;
(2)因为在第一问的前提下原代数式为3x2+8y2
当x=2,y=-1时,原式=3×22+8×(-1)2=12+8=20;
所以马小虎的结果是正确的;
故答案为:(1)k=7;(2)20;
变式:若已知,则 .
【解析】利用代数式整体代入的方法即可求出值;
【解答】∵;
∴
又∵
∴原式=
故答案为:
例6:一个两位数,十位上数字,个位上数字分别是.已知,现将十位上数字,个位上数字都减去3,所在位置不变组成一个新两位数.求原两位数与新两位数之和是多少
【解析】根据题意列出正确的代数式,然后代数式求和即可;
【解答】由题意知原来的两位数是,现在两个数都减去3,所得的新的两位数为:所以两个数求和所得的结果为:
故答案为:;
四、易错指津
一、选择题
1.单项式2a的系数是( )
A.2 B.2a C.1 D.a
2.下列计算正确的个数 ( ).
① ;② ; ③ ;
④ ; ⑤
A.2 B.1 C.4 D.0
3.现规定一种运算:a * b = ab + a - b,其中a,b为有理数,则3 * 5的值为( ).
A.11 B.12 C.13 D.14
4.化简(n为正整数)的结果为( ).
A.0 B.-2a C.2a D.2a或-2a
5.已知a-b=-3,c+d=2,则(b+c)-(a-d)为( ).
A.-1 B.-5 C.5 D.1
6. 有理数a,b,c在数轴上的位置如右图所示,则 ( ).
A.-2b B.0
C.2c D.2c-2b
7.当x=-3时,多项式的值是7,那么当x=3时,它的值是( ).
A.-3 B.-7 C.7 D.-17
8.如果是关于的二次三项式,那么m,n应满足的条件是( ).
A.m=1,n=5 B.m≠1,n>3
C.m≠-1,n为大于3的整数 D.m≠-1,n=5
五、课堂练习
1.是关于x,y的一个单项式,且系数是3,次数是4,则m=________,n=________.
2. (1)(___________);
(2)2a-3(b-c)=___________.
(3)(________)=7x+8.
3.当b=________时,式子2a+ab-5的值与a无关.
4.若,则________.
5.一台电视机原价是2500元,现按原价的8折出售,则购买a台这样的电视机需要 元.
6.当k=__________时,多项式x2-3kxy-3y2-xy-8中不含xy项.
7.若mn=m+3,则2mn+3m﹣5mn+10= .
8.如图,是用棋子摆成的图案,摆第1个图案需要7枚棋子,摆第2个图案需要19枚棋子,摆第3个图案需要37枚棋子,按照这样的方式摆下去,则摆第6个图案需要 枚棋子,摆第n个图案需要 枚棋子.
9.先化简,再求值.
(a2+1)﹣3a(a﹣1)+2(a2+a﹣1),其中a=﹣1.
10.观察下列一串单项式的特点:xy,﹣2x2y,4x3y,﹣8x4y,16x5y,…
(1)按此规律写出第9个单项式;
(2)试猜想第N个单项式为多少?它的系数和次数分别是多少?
11. 如图所示,用三种大小不同的六个正方形
和一个缺角的正方形拼成长方形ABCD,
其中,GH=2cm, GK=2cm, 设BF=x cm,
(1)用含x的代数式表示CM= cm,
DM= cm.
(2)若x=2cm,求长方形ABCD的面积.
12. 测得一弹簧的长度L(厘米)与悬挂物体的质量x(千克)有下面一组对应值:
试根据表中各对对应值解答下列问题:
(1)用代数式表示挂质量为x千克的物体时的弹簧的长度L.
(2)求所挂物体的质量为10千克时,弹簧的长度是多少?
(3)若测得弹簧的长度是18厘米,则所挂物体的质量为多少千克?
(4)若要求弹簧的长度不超过20厘米,则所挂物体的质量不能超过多少千克?
六、举一反三
一、选择题
1.已知a与b互为相反数,且x与y互为倒数,那么|a+b|-2xy的值为( ).
A.2 B.-2 C.-1 D.无法确定
2.多项式2a2b﹣ab2﹣ab的项数及次数分别是( )
A.3,3 B.3,2 C.2,3 D.2,2
3.在-3,π,-2,,,六个代数式中,是单项式的个数( )
A.2个 B.3个 C.4个 D.5个
4.对于式子,下列说法正确的是( ).
A.不是单项式
B.是单项式,系数为-1.2×10,次数是7
C.是单项式,系数为-1.2×104,次数是3
D.是单项式,系数为-1.2,次数是3
5.下面计算正确的是( )
A.3-=3 B.3+2=5 C.3+=3 D.-0.25+=0
6.2a-(5b-c+3d-e)=2a□5b□c□3d□e,方格内所填的符号依次是( ).
A.+,-,+,- B.-,-,+,-
C.-,+,-,+ D.-,+,-,-
7.某工厂现有工人a人,若现有工人数比两年前减少了35%,则该工厂两年前工人数为( ).
A. B.(1+35%)a C. D.(1-35%)a
8.若的值为8,则的值是( ).
A.2 B.-17 C.-7 D.7
二、填空题
9.端午节期间,“惠民超市”销售的粽子打8折后卖a元,则粽子的原价卖_______元.
10.单项式的系数是 ,次数是 .
11.是________次________项式,最高次项的系数是________.
12.化简:2a-(2a-1)=________.
13.如果,,那么________.
14.一个多项式减去3x等于,则这个多项式为________.
15.若与﹣3ab的和为单项式,则m+n= .
16.如图所示,外圆半径是R厘米,内圆半径是r厘米,四个小圆的半径都是2厘米,则图中阴影部分的面积是________平方厘米.
三、解答题
17.化简:
(1) (2)
18.已知:,,,当时,求代数式的值.
19.列式计算:一个多项式加上2x2﹣x+5等于4x2﹣6x﹣3,求这个多项式?
20.某农场有耕地1000亩,种粮食、棉花和蔬菜. 其中蔬菜用地a亩,粮食用地比蔬菜用地的6倍还多b亩,求棉花用地多少亩?当a=120,b=4时,棉花用地多少亩?
七、拓宽视野
法老问泰勒斯用什么工具来量金字塔。泰勒斯说只用一根木棍和一把尺子,他把木棍插在金字塔旁边,等木棍的影子和木棍一样长的时候,他量了金字塔影子的长度和金字塔底面边长的一半。把这两个长度加起来就是金字塔的高度了。泰勒斯真是世界上最聪明的人,他不用爬到金字塔的顶上就方便量出了金字塔的高度。
第十一讲 代数式的复习
【答案与解析】
四、易错指津
1.【答案】A.
2.【答案】D
3. 【答案】C
【解析】按规定的运算得:3*5=3×5+3-5=13.
4. 【答案】A
【解析】分析两种情况,当n为偶数时,,,当n为奇数时,,,无论哪种情况,结果都是0.
5.【答案】C
【解析】(b+c)-(a-d)=b+c-a+d=-a+b+c+d=-(a-b)+(c+d)
当a-b=-3,c+d=2时,原式=-(-3)+2=5,所以选C.
6.【答案】B
7. 【答案】D
【解析】由已知条件得:,通过适应变形得:
.当x=3时,原式,再把变形后的式子的值整体代入即可.
8.【答案】D
【解析】由题意得:n-3=2且m+1≠0,得n=5且m≠-1.
五、课堂练习
1.【答案】-3 , 3
【解析】由系数为3,得-m=3,则m=-3.由次数为4,得x,y的指数之和为4,即n+1=4,则n=3.
2.【答案】
3.【答案】-2
【解析】2a+ab-5=(2+b)a-5.因为式子的值与a无关,故2+b=0,所以b=-2.
4.【答案】-24
【解析】因为与互为相反数,又因为,
所以,由此可得.
5.【答案】2000a.
6.【答案】-;
【解析】,解得.
7.【答案】1;
【解析】解:原式=﹣3mn+3m+10,
把mn=m+3代入得:原式=﹣3m﹣9+3m+10=1,
故答案为:1.
8.【答案】127, .
【解析】∵第1个图形需要7=1+6×1枚棋子,
第2个比第1个多12个,即1+6×(1+2)枚,
第3个比第2个多18个,即1+6×(1+2+3)枚,
第4个比第三个多24个,即1+6×(1+2+3+4)=61枚,
……,
∴第n个比第(n-1)个多6n个,即1+6×(1+2+3+4+…+n)=3n2+3n+1枚.
9. 【解析】
解:原式=a2+1﹣3a2+3a+2a2+2a﹣2=5a﹣1,
当a=﹣1时,
原式=﹣5﹣1=﹣6.
10.【解析】
解:(1)∵当n=1时,xy,
当n=2时,﹣2x2y,
当n=3时,4x3y,
当n=4时,﹣8x4y,
当n=5时,16x5y,
∴第9个单项式是29﹣1x9y,即256x9y.
(2)∴n为偶数时,单项式为负数.x的指数为n时,2的指数为n﹣1,
∴当n为奇数时的单项式为2n﹣1xny,
它的系数是2n﹣1,次数是n+1.
11.【解析】
解:(1)(x+2),(2x+2)(或(3x)).
(2)长方形的长为: (cm),
宽为:(cm).
∴长方形的面积为:14×10=140 (cm2).
答:长方形ABCD的面积为140cm2 .
12.【解析】
解:(1).
(2)将,代入,得(㎝)
∴所挂物体的质量为10千克时,弹簧的长度是17㎝.
(3)将,代入,得,解得
∴若测得弹簧的长度是18厘米,则所挂物体的质量为12千克.
(4)∵弹簧的长度不超过20厘米,即L≤20,
∴≤20,得≤16.
∴若要求弹簧的长度不超过20厘米,则所挂物体的质量不能超过16千克.
六、举一反三
一、选择题
1. 【答案】B
【解析】根据已知条件,a与b互为相反数,即a+b=0,x与y互为倒数,即xy=1,所以|a+b|-2xy=0-2×1=-2,故选B.
2.【答案】A
【解析】2a2b﹣ab2﹣ab是三次三项式,故次数是3,项数是3.
3. 【答案】B
【解析】解:﹣3,﹣x2y是单项式.注意-2是分式.故选:B.
4.【答案】 C
【解析】此单项式的系数是以科学记数法形式出现的数,所以系数为-1.2×104,次数应为x与y的指数之和,不包括10的指数4,故次数为3.不要犯“见指数就相加”的错误.所以正确答案为C.
5. 【答案】D
6.【答案】 C
【解析】因为括号前是“-”号,所以去括号时,括号里各项都变号,故选C.
7. 【答案】C
【解析】把减少前的工人数看作整体“1”,已知一个数的(1-35%)是a,求这个数,则是,注意列式时不能用“÷”号,要写成分数形式.
8.【答案】C
【解析】,,,故.
二、填空题
9.【答案】.
10. 【答案】;
11.【答案】三, 三 , ;
【解析】多项式的次数取决于次数最高项的次数,确定系数时不要忽视前面的“-”号.
12.【答案】1;
【解析】先根据去括号法则去括号,然后合并同类项即可,2a-(2a-1)=2a-2a+1=1.
13.【答案】5;
【解析】用前式减去后式可得.
14.【答案】;
【解析】要求的多项式实际上是,化简可得出结果.
15.【答案】4;
【解析】解:∵与﹣3ab的和为单项式,
∴2m﹣5=1,n+1=3﹣n,
解得:m=3,n=1.
故m+n=4.
故答案为:4.
16.【答案】;
【解析】阴影部分的面积=大圆面积-最中间的圆的面积-4个小圆的面积.
三、解答题
17. 【解析】
解:(1)
原式==.
(2)
18.【解析】
解:∵ ∴
∴
当时,
.
19.【解析】
解:根据题意得:(4x2﹣6x﹣3)﹣(2x2﹣x+5)=4x2﹣6x﹣3﹣2x2+x﹣5=2x2﹣5x﹣8.
20.【解析】
解:棉花用地:1000-a-(6a+b)=(1000-7a-b)亩.
当a=120,b=4时,原式=1000-7×120-4
=156(亩).
答:棉花用地(1000-7a-b)亩.当a=120,b=4时,棉花用地为156亩.
…
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
