【备考2023】湖北省十堰市中考数学模拟试卷1(含解析)
文档属性
| 名称 | 【备考2023】湖北省十堰市中考数学模拟试卷1(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-09 15:01:47 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
【备考2023】湖北省十堰市中考数学模拟试卷1
姓名:__________班级:__________考号:__________总分__________
一、选择题(本题有10个小题,每小题3分,共30分)下面每小题给出的四个选项中,只有一个是正确的,请把正确选项的字母填涂在答题卡中相应的格子内.)
1.下列说法中错误的是( )
A.0的相反数是0 B.任何有理数都有相反数
C.a的相反数是﹣a D.表示相反意义的量的两个数互为相反数
2.如图,该几何体的俯视图是( )
A. B. C. D.
3.下列计算正确的是( )
A. B. C. D.
4.在墙壁上固定一根横放的木条,则至少需要钉子的枚数是( )
A.1枚 B.2枚 C.3枚 D.任意枚
5.为了解某公司员工的年基本工资情况,小王随机调查了10名员工,其年基本工资(单位:万元)如下:3,3,3,4,5,5,6,7,8,20.下列统计量中,能合理反映该公司员工年基本工资中等水平的是( )
A.方差 B.众数
C.中位数 D.平均数
6.古埃及人的“纸草书”中记载了一个数学问题:一个数,它的三分之二,它的一半,它的七分之一,它的全部,加起来总共是33.设这个数是x,则所列方程正确的为( )
A. B.
C. D.
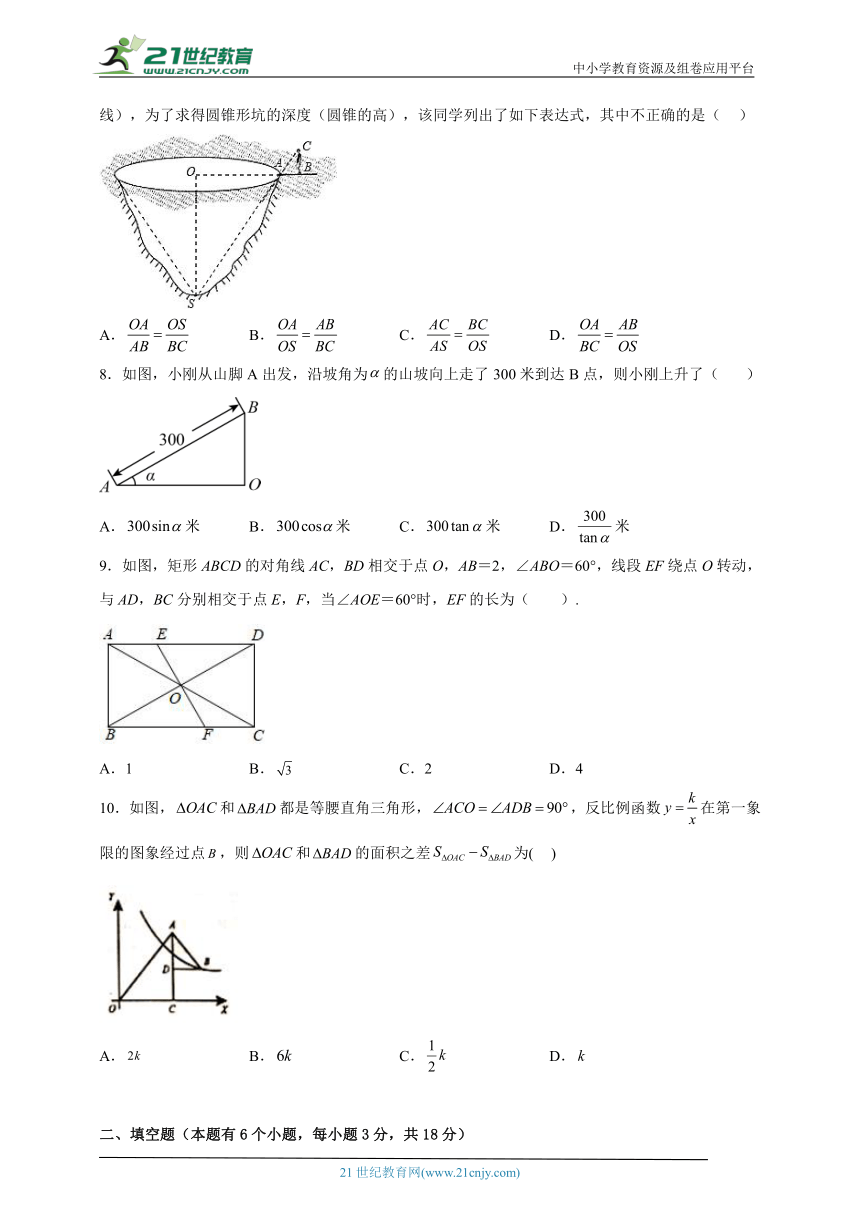
7.数学课外活动小组的同学们,带着皮尺去测量某河道因挖沙形成的“圆锥形坑”的深度(如图),点为沙坑底面所在圆的圆心,为其顶点,甲同学直立于沙坑坑沿的圆周所在的平面上,当他位于时,其视线恰好经过沙坑坑沿圆周上一点看到坑底(甲同学的视线起点与点,点三点共线),为了求得圆锥形坑的深度(圆锥的高),该同学列出了如下表达式,其中不正确的是( )
A. B. C. D.
8.如图,小刚从山脚A出发,沿坡角为的山坡向上走了300米到达B点,则小刚上升了( )
A.米 B.米 C.米 D.米
9.如图,矩形ABCD的对角线AC,BD相交于点O,AB=2,∠ABO=60°,线段EF绕点O转动,与AD,BC分别相交于点E,F,当∠AOE=60°时,EF的长为( ).
A.1 B. C.2 D.4
10.如图,和都是等腰直角三角形,,反比例函数在第一象限的图象经过点,则和的面积之差为( )
A. B. C. D.
二、填空题(本题有6个小题,每小题3分,共18分)
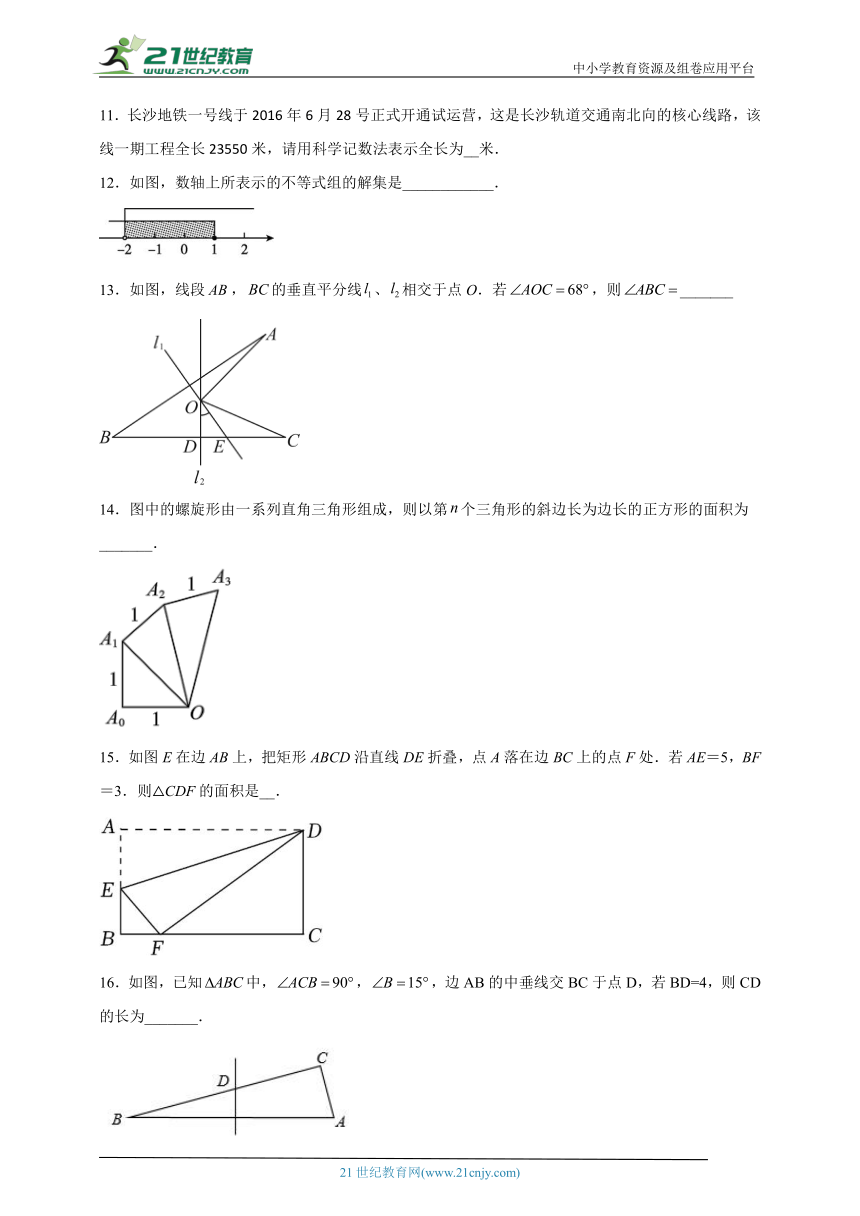
11.长沙地铁一号线于2016年6月28号正式开通试运营,这是长沙轨道交通南北向的核心线路,该线一期工程全长23550米,请用科学记数法表示全长为__米.
12.如图,数轴上所表示的不等式组的解集是____________.
13.如图,线段,的垂直平分线、相交于点O.若,则_______
14.图中的螺旋形由一系列直角三角形组成,则以第个三角形的斜边长为边长的正方形的面积为_______.
15.如图E在边AB上,把矩形ABCD沿直线DE折叠,点A落在边BC上的点F处.若AE=5,BF=3.则△CDF的面积是__.
16.如图,已知中,,,边AB的中垂线交BC于点D,若BD=4,则CD的长为_______.
三、解答题(本题有9个小题,共72分)
17.(1)解方程:;
(2)计算:
18.计算:
(1)(x﹣2)(x+2)﹣(x﹣2)2;
(2)(﹣1)÷.
19.已知关于x的方程有两个实数根
(1)求k的取值范围;
(2)若方程的两实数根分别为x1,x2,且x12+x22=6x1x2-15,求k的值.
20.市教育局想知道某中学学生对板桥博物馆的了解程度,在某中学随机抽取了部分学生进行问卷,问卷有以下四个选项:A.十分了解;B.了解较多;C.了解较少;D.不了解(要求:每名被调查的学生必选且只能选择一项).现将调查的结果绘制成两幅不完整的统计图.请根据两幅统计图中的信息回答下列问题:
(1)计算本次被抽取的学生数量;
(2)请补全条形统计图;
(3)计算扇形图中的选项“C.了解较少”部分所占扇形的圆心角的度数;
(4)若某中学共有4000名学生,请你根据上述调查结果估计该校对于板桥博物馆“十分了解”和“了解较多”的学生共有多少名?
21.在□中,点在上,点在上,连接.
(1)如图1,求证:四边形是平行四边形;
(2)如图2,连接平分,且,请直接写出长度等于长度的倍的线段.
22.如图,已知,OP是的平分线,点A是OM上一点,于点E交OP于点D,的平分线AG与OP交于点F.
(1)作点A关于OP对称点B(尺规作图,保留作图痕迹,不写作法);
(2)写出一个的值,使得对于射线OM上任意的点A总有(点A不与点O重合),并证明.
23.为了加快教育教学手段的现代化,某学校计划购置一批电脑,已知甲公司的报价是每台5800元,优惠条件是购买10台以上,则从11台开始按报价的计算;乙公司的报价也是每台5800元,优惠条件是每台均按报价的计算.
(1)当购买30台电脑时,在甲公司花费______元;在乙公司花费______元;
(2)假如你是学校有关方面负责人,在电脑品牌、质量、售后服务等完全相同的前提下,应如何根据购买电脑的数量选择比较合算的方案?请说明理由.
24.抛物线经过A、、三点.点D为抛物线的顶点,连接、、、.
(1)求抛物线的解析式;
(2)在y轴上是否存在一点E,使为直角三角形?若存在,请你直接写出点E的坐标;若不存在,请说明理由.
25.把两个等腰直角和按如图所示的位置摆放,,将绕点按逆时针方向旋转,如图,连接,,设旋转角为.
(1)求证:.
(2)如图3,若点在线段上,且,,求的长.
(3)当旋转角 时,的面积最大.
参考答案:
1.【分析】根据相反数的定义即可求解.
解:A中,0的相反数是0本身,故A不符合题意;
B中,任何有理数都有相反数,故B不符合题意;
C中,a的相反数是﹣a,故C不符合题意;
D中,只有符号不同的两个数叫做互为相反数.而表示相反意义的量的两个数可以用正数和负数表示.
故选D.
【点评】本题考查了相反数,只有符号不同的两个数叫做互为相反数,一个数的相反数就是在这个数前面添上“﹣”号:一个正数的相反数是负数,一个负数的相反数是正数,0的相反数是0.
2.【分析】根据俯视图是从上面看到的图形求解即可.
解:从上面看,看到的图形是一个长方形,在靠近右侧和靠近中间分别有1条竖直的直线,即看到的图形为
,
故选C.
【点评】本题主要考查了判断简单几何体的三视图,熟知俯视图是从上面看到的图形是解题的关键.
3.【分析】选项A,B,C按整式的加减法法则判断即可,选项D按去括号法判断即可.
解:A.,故选项A错误;
B.与3b不是同类项,不能再合并,故选项B错误;
C.与2ba2不是同类项,不能合并,故选项C错误;
D.,故选项D正确.
故选:D.
【点评】本题考查了整式的加减与去括号法则,正确理解同类项定义及合并同类项法则是解题的关键.
4.【分析】结合题意,根据两点确定一条直线的性质分析,即可得到答案.
解:在墙壁上固定一根横放的木条,则至少需要钉子的枚数是2,
故选:B.
【点评】本题考查了直线的知识;解题的关键是熟练掌握两点确定一条直线的性质,从而完成求解.
5.【分析】根据题意,结合员工工资情况,从统计量的角度分析可得答案.
解:根据题意,了解这家公司的员工的工资的中等水平,
结合员工情况表,即要全面的了解大多数员工的工资水平,
故最应该关注的数据的中位数,
故选:C.
【点评】此题主要考查统计的有关知识,主要包括平均数、中位数、众数、方差的意义.
6.【分析】可设这个数是x,根据等量关系:这个数的三分之二+这个数的一半+这个数的七分之一+这个数=33,依此列出方程求解即可.
解:由题意可得:,
故选:C.
【点评】此题主要考查了由实际问题抽象出一元一次方程,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系列出方程.
7.【分析】根据已知条件先证明,根据相似三角形的性质,进行判断即可.
解:∵点O为沙坑底面所在圆的圆心,S为其顶点,
∴,
∵甲同学直立于沙坑坑沿的圆周所在的平面上,
∴,
∴,
∵视线起点C与点A,点S三点共线,
∴,
∴,
∴,
即,,,故ABC正确,不符合题意;
无法判断,故D错误,符合题意.
故选:D.
【点评】本题主要考查了相似三角形的判定和性质,根据题目中的已知条件得出,是解题的关键.
8.【分析】利用锐角三角函数关系即可求出小刚上升了的高度.
解:在Rt△AOB中,∠AOB=90°,AB=300米,
BO=AB sinα=300sinα米.
故选A.
【点评】此题主要考查了解直角三角形的应用,根据题意构造直角三角形,正确选择锐角三角函数得出AB,BO的关系是解题关键.
9.【分析】证得△ABO为等边三角形,得出∠BAO=60°,由三角形内角和求出∠AEO=90°,得出四边形ABFE为矩形,则可得出答案.
解:∵四边形ABCD是矩形,
∴OA=OB,∠ABC=∠BAD=90°,
又∵∠ABO=60°,
∴△ABO为等边三角形,
∴∠BAO=60°,
∴∠OAE=30°,
∵线段EF绕点O转动,∠AOE=60°,
∴∠AEO=180°﹣60°﹣30°=90°,
∴四边形ABFE为矩形,
∴AB=EF=2.
故选:C.
【点评】本题考查了矩形的判定与性质,等边三角形的判定与性质等知识,熟练掌握等边三角形的判定与性质是解题的关键.
10.【分析】设△OAC和△BAD的直角边长分别为a、b,结合等腰直角三角形的性质及图象可得出点B的坐标,根据三角形的面积公式结合反比例函数系数k的几何意义以及点B的坐标即可得出结论.
解:设△OAC和△BAD的直角边长分别为a、b,
则点B的坐标为(a+b,a b).
∵点B在反比例函数的第一象限图象上,
∴
∴
故选C.
【点评】考查反比例函数系数k的几何意义, 等腰直角三角形,掌握等腰直角三角形的性质是解题的关键.
11.解:【分析】科学记数法:把一个大于10的数记为a×10n的形式(其中1≤| a| <10)的记数法
解:23550=2.355×104
故答案为2.355×104
【点评】本题考核知识点:科学记数法.解题关键点:熟记科学记数法定义.
12.【分析】根据数轴所示即可得到答案,实心圆点包括该点,空心圆圈不包括该点,大于向右小于向左.
解:由图示可看出,从-2出发向右画出的线且-2处是空心圆,表示x>-2;
从1出发向左画出的线且1处是实心圆,表示x≤1,不等式组的解集是指它们的公共部分.
所以这个不等式组的解集是:-2<x≤1.
故答案为-2<x≤1.
【点评】本题考查了不等式的解集在数轴上表示的方法,解题的关键是看清实心点和空心点,才能保证答案的准确.
13.【分析】连接,,根据,,得出,,求出,根据,求出,即可得出.
解:连接,,如图所示:
∵线段,的垂直平分线、相交于点O,
∴,,
∴,,
∵,
∴,
∵,
∴,
∴,
∴,
即.
故答案为:.
【点评】本题主要考查了垂直平分线的性质,等腰三角形的性质,三角形内角和定理的应用,解题的关键是作出辅助线,熟练掌握线段垂直平分线上的点到线段两个端点的距离相等.
14.【分析】根据勾股定理的几何意义解答.
解:第n个三角形的斜边长为边长的正方形的面积即为第n个三角形的斜边长的平方.
第一个三角形的斜边长OA1==,
第二个三角形的斜边长OA2==,
同理:OA3=,
…,
∴OAn=,
则第n个的斜边长为边长的正方形的面积为n+1.
故答案为:n+1.
【点评】本题考查了图形类规律,勾股定理,通过计算找出规律,再根据规律解题.
15.【分析】根据折叠对称的性质可得AE=EF,勾股定理求得BE,在RtFCD中求出FC,再根据三角形面积公式即可求得.
解:设BC为x则AD=FD=x.
∵矩形ABCD沿直线DE折叠,点A落在边BC上的点F处,
∴AE=EF=5
∵在RtEBF中,BF=3
∴BE=4
∴AB=CD=9
在RtFCD中,FC=x-3,CD=9,FD=x
由勾股定理可得
解得x=15
∴
故答案为:54.
【点评】此题考查了折叠的对称性、勾股定理、矩形的性质,解题的关键是利用勾股定理求得边长.
16.【分析】连接AD,根据中垂线的性质可得AD=4,进而得到,,最后根据勾股定理即可求解.
解:连接AD
∵边AB的中垂线交BC于点D, BD=4
∴AD=4
∵,
∴
∴
∴
故答案为:.
【点评】此题主要考查中垂线的性质、角所对的直角边等于斜边的一半、勾股定理,熟练掌握性质是解题关键.
17.【分析】(1)根据解一元一次方程的方法步骤求解即可;
(2)先计算有理数的乘方运算,化简绝对值,然后计算乘除法,最后计算加减法即可.
解:(1)
去括号得
移项得,
合并同类项得,
系数化为1得.
(2)
.
【点评】题目主要考查解一元一次方程,含乘方的有理数的混合运算,熟练掌握运算法则是解题关键.
18.【分析】(1)先利用平方差公式以及完全平方公式去括号,再合并同类项即可求出答案;
(2)先根据分式的加减法法则计算括号内的,再根据分式的乘除法法则计算即可求出答案.
解:(1)原式
;
(2)原式
.
【点评】本题考查整式的混合运算以及分式的混合运算,熟练掌握相关运算法则以及乘法公式是解决本题的关键,本题属于基础题型.
19.【分析】(1)由方程根的情况,根据根的判别式可得到关于k的不等式,则可求得k的取值范围;
(2)由根与系数的关系可用k表示出x1+x2和x1 x2,利用已知条件可得到关于k的方程,可求得k的值.
解:(1)∵关于x的方程有两个实数根,
∴,解得;
(2)
∵方程的两实数根分别为x1,x2,
∴x1+x2=k+1,,
∵x12+x22=6x1x2-15,
∴(x1+x2)2-8x1x2+15=0,
∴k2-2k-8=0,解得:k1=4,k2=-2,
又∵,
∴k=4.
【点评】本题主要考查一元二次方程根的判别及根与系数的关系,掌握相关知识是解本题的关键.
20. 【分析】(1)从两个统计图可知,“了解较少”的人数为30人,占调查人数的,根据频率可求出调查人数;
(2)求出“了解较多”的人数即可补全条形统计图;
(3)由于“了解较少”所占得出人数的,因此相应圆心角的度数占的即可;
(4)求出“十分了解”和“了解较多”共占调查人数的百分比,进而估计总体的百分比,再进行计算即可.
解:(1)解:(人)
答:本次被抽取的学生数量是100人;
(2)解:“了解较多”的人数为:(名,
补全条形统计图如下:
(3)解:,
答:扇形图中的选项“C.了解较少”部分所占扇形的圆心角的度数为108°;
(4)解:(名),
答:该校对于板桥博物馆“十分了解”和“了解较多”的学生大约有2400名.
【点评】本题考查条形统计图,扇形统计图,掌握两个统计图中数量之间的关系是正确解答的前提.
21.【分析】(1)由平行四边形的性质得出AB∥CD,∠ADE=∠CBF,AD=BC,由ASA证明△ADE≌△CBF,得出DE=BF,即可得出四边形DFBE是平行四边形;
(2)通过证明四边形AECF是菱形,可得AE=CE=CF=AF=2DE.
解:(1)∵四边形ABCD是平行四边形,
∴AB∥CD,∠ADE=∠CBF,AD=BC,
∵∠DAE=∠BCF,AD=BC,∠ADE=∠CBF,
∴△ADE≌△CBF(ASA),
∴DE=BF,
又∵DE∥BF,
∴四边形DFBE是平行四边形;
(2)有:AE,AF,CE,CF
理由如下:∵AB=3DE,
∴AB=3BF
∴AF=2BF=2DE
∵CD=AB,DE=BF
∴EC=AF,且CD∥AB
∴四边形AFCE是平行四边形
∵EF平分∠AEC
∴∠AEF=∠CEF,
∵CD∥AB
∴∠CEF=∠AFE
∴∠AEF=∠AFE
∴AF=AE,
∴平行四边形AECF是菱形
∴AE=CE=CF=AF=2DE.
【点评】此题考查平行四边形的性质与判定,全等三角形的判定与性质,菱形的判定和性质,利用全等三角形的性质证明线段相等是解题的关键.
22.【分析】(1)以O为圆心,AO长为半径画圆,根据等腰三角形的三线合一可得圆与射线ON交点即为B;
(2)当时总有,只需证明AB=OD=2AC, 即可.
解:(1)图形如图所示,点B即为所求:
(2)当时使得对于射线OM上任意的点A总有,证明如下:
设AB交OP于C
∵
∴
∴
∵OP是的平分线,的平分线AG与OP交于点F
∴
由(1)得OA=OB
∴AB⊥OP,AB=2AC
∴
∴
∴
在△ODE和△ABE中
,
∴(ASA)
∴OD=AB
∴
【点评】本题考查全等三角形的综合,熟记等腰三角形三线合一性质、等腰直角三角形特点是解题的关键.
23.【分析】(1)根据题意分别计算,即可求解;
(2)分三种情况,分别列不等式及方程,即可求解.
(1)解:当购买30台电脑时,在甲公司花费为:(元),
在乙公司花费为:(元),
故答案为:139200,147900;
(2)解:由题意可知,当购买电脑数量不超过10台时,去乙公司购买合算;
当购买电脑数量超过10台时,设电脑购买数量为台
若去甲公司购买合算,则
解得
若去乙公司购买合算,则
解得
若去甲、乙公司购买费用相同,则
解得
答:当购买多于20台电脑时,去甲公司合算;当购买少于20台电脑时,去乙公司合算;当购买20台电脑时,去甲、乙两公司费用相同.
【点评】本题考查了一元一次方程及不等式的应用,有理数混合运算的应用,解题的关键是:根据各数量之间的关系,正确列出一元一次不等式.
24.【分析】(1)利用待定系数法求解即可;
(2)分三种情况:,,讨论即可.
(1)解:∵经过、,
∴,解得,
∴抛物线的解析式为:;
(2)解:在y轴上存在点E,使为直角三角形,理由如下:
∵抛物线的解析式为,
∴,
设E点坐标为,
∴,,,
当时,有,
∴,
解得,
∴此时点E的坐标为;
当时,,
,
解得,
∴此时点E的坐标为;
当时,,
,
解得或,
∴此时点E的坐标为或.
综上所述,符合题意的点E的坐标为或或或.
【点评】本题考查了二次函数与特殊三角形,掌握待定系数法,勾股定理等知识是解题的关键.
25.【分析】(1)根据等腰三角形性质得出,,根据角度差得出,即可证明;
(2)过点作于,由证明同理可得,根据等腰直角三角形的性质得出是斜边中线,在中,,在中,勾股定理得出,根据,进而即可求解;
(3)点轨迹在以为圆心,为半径的圆上,得出当时,面积最大,即点在直线上,根据题意,面积最大,进而画出图形即可求解.
(1)证明:,都是等腰直角三角形,
,,
,
则,
,
;
(2)解:如图,过点作于,
由证明同理可得,
,
是等腰直角三角形,,
是斜边中线,
,
在中,,,
,
在中,,
∴,
;
(3)解:点轨迹在以为圆心,为半径的圆上,
的长度为定值,
的长度为定值,
底边上的高,
当时,面积最大,即点在直线上,
①如图当时,,面积最大,
②如图,当时,,面积最大,
当为或时,面积最大;
故答案为:或.
【点评】本题考查了旋转的性质,等腰直角三角形的性质,全等三角形的性质与判定,三角形面积,解直角三角形,勾股定理,熟练掌握以上知识是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
【备考2023】湖北省十堰市中考数学模拟试卷1
姓名:__________班级:__________考号:__________总分__________
一、选择题(本题有10个小题,每小题3分,共30分)下面每小题给出的四个选项中,只有一个是正确的,请把正确选项的字母填涂在答题卡中相应的格子内.)
1.下列说法中错误的是( )
A.0的相反数是0 B.任何有理数都有相反数
C.a的相反数是﹣a D.表示相反意义的量的两个数互为相反数
2.如图,该几何体的俯视图是( )
A. B. C. D.
3.下列计算正确的是( )
A. B. C. D.
4.在墙壁上固定一根横放的木条,则至少需要钉子的枚数是( )
A.1枚 B.2枚 C.3枚 D.任意枚
5.为了解某公司员工的年基本工资情况,小王随机调查了10名员工,其年基本工资(单位:万元)如下:3,3,3,4,5,5,6,7,8,20.下列统计量中,能合理反映该公司员工年基本工资中等水平的是( )
A.方差 B.众数
C.中位数 D.平均数
6.古埃及人的“纸草书”中记载了一个数学问题:一个数,它的三分之二,它的一半,它的七分之一,它的全部,加起来总共是33.设这个数是x,则所列方程正确的为( )
A. B.
C. D.
7.数学课外活动小组的同学们,带着皮尺去测量某河道因挖沙形成的“圆锥形坑”的深度(如图),点为沙坑底面所在圆的圆心,为其顶点,甲同学直立于沙坑坑沿的圆周所在的平面上,当他位于时,其视线恰好经过沙坑坑沿圆周上一点看到坑底(甲同学的视线起点与点,点三点共线),为了求得圆锥形坑的深度(圆锥的高),该同学列出了如下表达式,其中不正确的是( )
A. B. C. D.
8.如图,小刚从山脚A出发,沿坡角为的山坡向上走了300米到达B点,则小刚上升了( )
A.米 B.米 C.米 D.米
9.如图,矩形ABCD的对角线AC,BD相交于点O,AB=2,∠ABO=60°,线段EF绕点O转动,与AD,BC分别相交于点E,F,当∠AOE=60°时,EF的长为( ).
A.1 B. C.2 D.4
10.如图,和都是等腰直角三角形,,反比例函数在第一象限的图象经过点,则和的面积之差为( )
A. B. C. D.
二、填空题(本题有6个小题,每小题3分,共18分)
11.长沙地铁一号线于2016年6月28号正式开通试运营,这是长沙轨道交通南北向的核心线路,该线一期工程全长23550米,请用科学记数法表示全长为__米.
12.如图,数轴上所表示的不等式组的解集是____________.
13.如图,线段,的垂直平分线、相交于点O.若,则_______
14.图中的螺旋形由一系列直角三角形组成,则以第个三角形的斜边长为边长的正方形的面积为_______.
15.如图E在边AB上,把矩形ABCD沿直线DE折叠,点A落在边BC上的点F处.若AE=5,BF=3.则△CDF的面积是__.
16.如图,已知中,,,边AB的中垂线交BC于点D,若BD=4,则CD的长为_______.
三、解答题(本题有9个小题,共72分)
17.(1)解方程:;
(2)计算:
18.计算:
(1)(x﹣2)(x+2)﹣(x﹣2)2;
(2)(﹣1)÷.
19.已知关于x的方程有两个实数根
(1)求k的取值范围;
(2)若方程的两实数根分别为x1,x2,且x12+x22=6x1x2-15,求k的值.
20.市教育局想知道某中学学生对板桥博物馆的了解程度,在某中学随机抽取了部分学生进行问卷,问卷有以下四个选项:A.十分了解;B.了解较多;C.了解较少;D.不了解(要求:每名被调查的学生必选且只能选择一项).现将调查的结果绘制成两幅不完整的统计图.请根据两幅统计图中的信息回答下列问题:
(1)计算本次被抽取的学生数量;
(2)请补全条形统计图;
(3)计算扇形图中的选项“C.了解较少”部分所占扇形的圆心角的度数;
(4)若某中学共有4000名学生,请你根据上述调查结果估计该校对于板桥博物馆“十分了解”和“了解较多”的学生共有多少名?
21.在□中,点在上,点在上,连接.
(1)如图1,求证:四边形是平行四边形;
(2)如图2,连接平分,且,请直接写出长度等于长度的倍的线段.
22.如图,已知,OP是的平分线,点A是OM上一点,于点E交OP于点D,的平分线AG与OP交于点F.
(1)作点A关于OP对称点B(尺规作图,保留作图痕迹,不写作法);
(2)写出一个的值,使得对于射线OM上任意的点A总有(点A不与点O重合),并证明.
23.为了加快教育教学手段的现代化,某学校计划购置一批电脑,已知甲公司的报价是每台5800元,优惠条件是购买10台以上,则从11台开始按报价的计算;乙公司的报价也是每台5800元,优惠条件是每台均按报价的计算.
(1)当购买30台电脑时,在甲公司花费______元;在乙公司花费______元;
(2)假如你是学校有关方面负责人,在电脑品牌、质量、售后服务等完全相同的前提下,应如何根据购买电脑的数量选择比较合算的方案?请说明理由.
24.抛物线经过A、、三点.点D为抛物线的顶点,连接、、、.
(1)求抛物线的解析式;
(2)在y轴上是否存在一点E,使为直角三角形?若存在,请你直接写出点E的坐标;若不存在,请说明理由.
25.把两个等腰直角和按如图所示的位置摆放,,将绕点按逆时针方向旋转,如图,连接,,设旋转角为.
(1)求证:.
(2)如图3,若点在线段上,且,,求的长.
(3)当旋转角 时,的面积最大.
参考答案:
1.【分析】根据相反数的定义即可求解.
解:A中,0的相反数是0本身,故A不符合题意;
B中,任何有理数都有相反数,故B不符合题意;
C中,a的相反数是﹣a,故C不符合题意;
D中,只有符号不同的两个数叫做互为相反数.而表示相反意义的量的两个数可以用正数和负数表示.
故选D.
【点评】本题考查了相反数,只有符号不同的两个数叫做互为相反数,一个数的相反数就是在这个数前面添上“﹣”号:一个正数的相反数是负数,一个负数的相反数是正数,0的相反数是0.
2.【分析】根据俯视图是从上面看到的图形求解即可.
解:从上面看,看到的图形是一个长方形,在靠近右侧和靠近中间分别有1条竖直的直线,即看到的图形为
,
故选C.
【点评】本题主要考查了判断简单几何体的三视图,熟知俯视图是从上面看到的图形是解题的关键.
3.【分析】选项A,B,C按整式的加减法法则判断即可,选项D按去括号法判断即可.
解:A.,故选项A错误;
B.与3b不是同类项,不能再合并,故选项B错误;
C.与2ba2不是同类项,不能合并,故选项C错误;
D.,故选项D正确.
故选:D.
【点评】本题考查了整式的加减与去括号法则,正确理解同类项定义及合并同类项法则是解题的关键.
4.【分析】结合题意,根据两点确定一条直线的性质分析,即可得到答案.
解:在墙壁上固定一根横放的木条,则至少需要钉子的枚数是2,
故选:B.
【点评】本题考查了直线的知识;解题的关键是熟练掌握两点确定一条直线的性质,从而完成求解.
5.【分析】根据题意,结合员工工资情况,从统计量的角度分析可得答案.
解:根据题意,了解这家公司的员工的工资的中等水平,
结合员工情况表,即要全面的了解大多数员工的工资水平,
故最应该关注的数据的中位数,
故选:C.
【点评】此题主要考查统计的有关知识,主要包括平均数、中位数、众数、方差的意义.
6.【分析】可设这个数是x,根据等量关系:这个数的三分之二+这个数的一半+这个数的七分之一+这个数=33,依此列出方程求解即可.
解:由题意可得:,
故选:C.
【点评】此题主要考查了由实际问题抽象出一元一次方程,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系列出方程.
7.【分析】根据已知条件先证明,根据相似三角形的性质,进行判断即可.
解:∵点O为沙坑底面所在圆的圆心,S为其顶点,
∴,
∵甲同学直立于沙坑坑沿的圆周所在的平面上,
∴,
∴,
∵视线起点C与点A,点S三点共线,
∴,
∴,
∴,
即,,,故ABC正确,不符合题意;
无法判断,故D错误,符合题意.
故选:D.
【点评】本题主要考查了相似三角形的判定和性质,根据题目中的已知条件得出,是解题的关键.
8.【分析】利用锐角三角函数关系即可求出小刚上升了的高度.
解:在Rt△AOB中,∠AOB=90°,AB=300米,
BO=AB sinα=300sinα米.
故选A.
【点评】此题主要考查了解直角三角形的应用,根据题意构造直角三角形,正确选择锐角三角函数得出AB,BO的关系是解题关键.
9.【分析】证得△ABO为等边三角形,得出∠BAO=60°,由三角形内角和求出∠AEO=90°,得出四边形ABFE为矩形,则可得出答案.
解:∵四边形ABCD是矩形,
∴OA=OB,∠ABC=∠BAD=90°,
又∵∠ABO=60°,
∴△ABO为等边三角形,
∴∠BAO=60°,
∴∠OAE=30°,
∵线段EF绕点O转动,∠AOE=60°,
∴∠AEO=180°﹣60°﹣30°=90°,
∴四边形ABFE为矩形,
∴AB=EF=2.
故选:C.
【点评】本题考查了矩形的判定与性质,等边三角形的判定与性质等知识,熟练掌握等边三角形的判定与性质是解题的关键.
10.【分析】设△OAC和△BAD的直角边长分别为a、b,结合等腰直角三角形的性质及图象可得出点B的坐标,根据三角形的面积公式结合反比例函数系数k的几何意义以及点B的坐标即可得出结论.
解:设△OAC和△BAD的直角边长分别为a、b,
则点B的坐标为(a+b,a b).
∵点B在反比例函数的第一象限图象上,
∴
∴
故选C.
【点评】考查反比例函数系数k的几何意义, 等腰直角三角形,掌握等腰直角三角形的性质是解题的关键.
11.解:【分析】科学记数法:把一个大于10的数记为a×10n的形式(其中1≤| a| <10)的记数法
解:23550=2.355×104
故答案为2.355×104
【点评】本题考核知识点:科学记数法.解题关键点:熟记科学记数法定义.
12.【分析】根据数轴所示即可得到答案,实心圆点包括该点,空心圆圈不包括该点,大于向右小于向左.
解:由图示可看出,从-2出发向右画出的线且-2处是空心圆,表示x>-2;
从1出发向左画出的线且1处是实心圆,表示x≤1,不等式组的解集是指它们的公共部分.
所以这个不等式组的解集是:-2<x≤1.
故答案为-2<x≤1.
【点评】本题考查了不等式的解集在数轴上表示的方法,解题的关键是看清实心点和空心点,才能保证答案的准确.
13.【分析】连接,,根据,,得出,,求出,根据,求出,即可得出.
解:连接,,如图所示:
∵线段,的垂直平分线、相交于点O,
∴,,
∴,,
∵,
∴,
∵,
∴,
∴,
∴,
即.
故答案为:.
【点评】本题主要考查了垂直平分线的性质,等腰三角形的性质,三角形内角和定理的应用,解题的关键是作出辅助线,熟练掌握线段垂直平分线上的点到线段两个端点的距离相等.
14.【分析】根据勾股定理的几何意义解答.
解:第n个三角形的斜边长为边长的正方形的面积即为第n个三角形的斜边长的平方.
第一个三角形的斜边长OA1==,
第二个三角形的斜边长OA2==,
同理:OA3=,
…,
∴OAn=,
则第n个的斜边长为边长的正方形的面积为n+1.
故答案为:n+1.
【点评】本题考查了图形类规律,勾股定理,通过计算找出规律,再根据规律解题.
15.【分析】根据折叠对称的性质可得AE=EF,勾股定理求得BE,在RtFCD中求出FC,再根据三角形面积公式即可求得.
解:设BC为x则AD=FD=x.
∵矩形ABCD沿直线DE折叠,点A落在边BC上的点F处,
∴AE=EF=5
∵在RtEBF中,BF=3
∴BE=4
∴AB=CD=9
在RtFCD中,FC=x-3,CD=9,FD=x
由勾股定理可得
解得x=15
∴
故答案为:54.
【点评】此题考查了折叠的对称性、勾股定理、矩形的性质,解题的关键是利用勾股定理求得边长.
16.【分析】连接AD,根据中垂线的性质可得AD=4,进而得到,,最后根据勾股定理即可求解.
解:连接AD
∵边AB的中垂线交BC于点D, BD=4
∴AD=4
∵,
∴
∴
∴
故答案为:.
【点评】此题主要考查中垂线的性质、角所对的直角边等于斜边的一半、勾股定理,熟练掌握性质是解题关键.
17.【分析】(1)根据解一元一次方程的方法步骤求解即可;
(2)先计算有理数的乘方运算,化简绝对值,然后计算乘除法,最后计算加减法即可.
解:(1)
去括号得
移项得,
合并同类项得,
系数化为1得.
(2)
.
【点评】题目主要考查解一元一次方程,含乘方的有理数的混合运算,熟练掌握运算法则是解题关键.
18.【分析】(1)先利用平方差公式以及完全平方公式去括号,再合并同类项即可求出答案;
(2)先根据分式的加减法法则计算括号内的,再根据分式的乘除法法则计算即可求出答案.
解:(1)原式
;
(2)原式
.
【点评】本题考查整式的混合运算以及分式的混合运算,熟练掌握相关运算法则以及乘法公式是解决本题的关键,本题属于基础题型.
19.【分析】(1)由方程根的情况,根据根的判别式可得到关于k的不等式,则可求得k的取值范围;
(2)由根与系数的关系可用k表示出x1+x2和x1 x2,利用已知条件可得到关于k的方程,可求得k的值.
解:(1)∵关于x的方程有两个实数根,
∴,解得;
(2)
∵方程的两实数根分别为x1,x2,
∴x1+x2=k+1,,
∵x12+x22=6x1x2-15,
∴(x1+x2)2-8x1x2+15=0,
∴k2-2k-8=0,解得:k1=4,k2=-2,
又∵,
∴k=4.
【点评】本题主要考查一元二次方程根的判别及根与系数的关系,掌握相关知识是解本题的关键.
20. 【分析】(1)从两个统计图可知,“了解较少”的人数为30人,占调查人数的,根据频率可求出调查人数;
(2)求出“了解较多”的人数即可补全条形统计图;
(3)由于“了解较少”所占得出人数的,因此相应圆心角的度数占的即可;
(4)求出“十分了解”和“了解较多”共占调查人数的百分比,进而估计总体的百分比,再进行计算即可.
解:(1)解:(人)
答:本次被抽取的学生数量是100人;
(2)解:“了解较多”的人数为:(名,
补全条形统计图如下:
(3)解:,
答:扇形图中的选项“C.了解较少”部分所占扇形的圆心角的度数为108°;
(4)解:(名),
答:该校对于板桥博物馆“十分了解”和“了解较多”的学生大约有2400名.
【点评】本题考查条形统计图,扇形统计图,掌握两个统计图中数量之间的关系是正确解答的前提.
21.【分析】(1)由平行四边形的性质得出AB∥CD,∠ADE=∠CBF,AD=BC,由ASA证明△ADE≌△CBF,得出DE=BF,即可得出四边形DFBE是平行四边形;
(2)通过证明四边形AECF是菱形,可得AE=CE=CF=AF=2DE.
解:(1)∵四边形ABCD是平行四边形,
∴AB∥CD,∠ADE=∠CBF,AD=BC,
∵∠DAE=∠BCF,AD=BC,∠ADE=∠CBF,
∴△ADE≌△CBF(ASA),
∴DE=BF,
又∵DE∥BF,
∴四边形DFBE是平行四边形;
(2)有:AE,AF,CE,CF
理由如下:∵AB=3DE,
∴AB=3BF
∴AF=2BF=2DE
∵CD=AB,DE=BF
∴EC=AF,且CD∥AB
∴四边形AFCE是平行四边形
∵EF平分∠AEC
∴∠AEF=∠CEF,
∵CD∥AB
∴∠CEF=∠AFE
∴∠AEF=∠AFE
∴AF=AE,
∴平行四边形AECF是菱形
∴AE=CE=CF=AF=2DE.
【点评】此题考查平行四边形的性质与判定,全等三角形的判定与性质,菱形的判定和性质,利用全等三角形的性质证明线段相等是解题的关键.
22.【分析】(1)以O为圆心,AO长为半径画圆,根据等腰三角形的三线合一可得圆与射线ON交点即为B;
(2)当时总有,只需证明AB=OD=2AC, 即可.
解:(1)图形如图所示,点B即为所求:
(2)当时使得对于射线OM上任意的点A总有,证明如下:
设AB交OP于C
∵
∴
∴
∵OP是的平分线,的平分线AG与OP交于点F
∴
由(1)得OA=OB
∴AB⊥OP,AB=2AC
∴
∴
∴
在△ODE和△ABE中
,
∴(ASA)
∴OD=AB
∴
【点评】本题考查全等三角形的综合,熟记等腰三角形三线合一性质、等腰直角三角形特点是解题的关键.
23.【分析】(1)根据题意分别计算,即可求解;
(2)分三种情况,分别列不等式及方程,即可求解.
(1)解:当购买30台电脑时,在甲公司花费为:(元),
在乙公司花费为:(元),
故答案为:139200,147900;
(2)解:由题意可知,当购买电脑数量不超过10台时,去乙公司购买合算;
当购买电脑数量超过10台时,设电脑购买数量为台
若去甲公司购买合算,则
解得
若去乙公司购买合算,则
解得
若去甲、乙公司购买费用相同,则
解得
答:当购买多于20台电脑时,去甲公司合算;当购买少于20台电脑时,去乙公司合算;当购买20台电脑时,去甲、乙两公司费用相同.
【点评】本题考查了一元一次方程及不等式的应用,有理数混合运算的应用,解题的关键是:根据各数量之间的关系,正确列出一元一次不等式.
24.【分析】(1)利用待定系数法求解即可;
(2)分三种情况:,,讨论即可.
(1)解:∵经过、,
∴,解得,
∴抛物线的解析式为:;
(2)解:在y轴上存在点E,使为直角三角形,理由如下:
∵抛物线的解析式为,
∴,
设E点坐标为,
∴,,,
当时,有,
∴,
解得,
∴此时点E的坐标为;
当时,,
,
解得,
∴此时点E的坐标为;
当时,,
,
解得或,
∴此时点E的坐标为或.
综上所述,符合题意的点E的坐标为或或或.
【点评】本题考查了二次函数与特殊三角形,掌握待定系数法,勾股定理等知识是解题的关键.
25.【分析】(1)根据等腰三角形性质得出,,根据角度差得出,即可证明;
(2)过点作于,由证明同理可得,根据等腰直角三角形的性质得出是斜边中线,在中,,在中,勾股定理得出,根据,进而即可求解;
(3)点轨迹在以为圆心,为半径的圆上,得出当时,面积最大,即点在直线上,根据题意,面积最大,进而画出图形即可求解.
(1)证明:,都是等腰直角三角形,
,,
,
则,
,
;
(2)解:如图,过点作于,
由证明同理可得,
,
是等腰直角三角形,,
是斜边中线,
,
在中,,,
,
在中,,
∴,
;
(3)解:点轨迹在以为圆心,为半径的圆上,
的长度为定值,
的长度为定值,
底边上的高,
当时,面积最大,即点在直线上,
①如图当时,,面积最大,
②如图,当时,,面积最大,
当为或时,面积最大;
故答案为:或.
【点评】本题考查了旋转的性质,等腰直角三角形的性质,全等三角形的性质与判定,三角形面积,解直角三角形,勾股定理,熟练掌握以上知识是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
