常考专题:正比例和反比例(单元测试) 小学数学六年级下册苏教版(含答案)
文档属性
| 名称 | 常考专题:正比例和反比例(单元测试) 小学数学六年级下册苏教版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-10 15:29:59 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
常考专题:正比例和反比例(单元测试)-小学数学六年级下册苏教版
一、选择题
1.一袋纯牛奶2.5元,购买纯牛奶的袋数和总钱数( )。
A.成正比例 B.成反比例 C.不成比例
2.张佳的淘宝店儿在“三八节”这天准备了足量的服装,卖出的件数和剩下的件数( )。
A.成正比例 B.成反比例 C.不成比例
3.下面两种相关联的量不成正比例的是( )。
A.圆的半径和周长 B.正方形的边长和面积 C.=y
4.一个圆的半径与周长( )。
A.成正比例 B.成反比例 C.不成比例
5.下面两种相关联的量中,不成比例关系的是( )。
A.平行四边形的面积一定,它的底和高
B.除数一定,被除数和商
C.人的身高和年龄
6.一包薯条,吃掉的数量和余下的数量( )。
A.成正比例 B.成反比例 C.不成比例
二、填空题
7.圆柱的高一定,圆柱的侧面积和底面周长成( )比例。
8.做的零件个数一定,做一个零件所用的时间和加工的总时间成( )比例。
9.A、B、C是三个顺次啮合的齿轮。已知齿轮A旋转7圈时,齿轮C旋转了6圈,如果A的齿数为42,那么C的齿数是( );如果B旋转7圈,C旋转1圈;那么当A旋转8圈时,B旋转( )圈。
10.如果=2,=,其中a,b,c都是大于0的数,那么a和c成( )比例。
11.如图,大长方形被分成了四个小长方形,其实三个小长方形的面积分别为30平方厘米、45平方厘米、18平方厘米,第四个小长方形的面积是( )平方厘米。
12.甲、乙是两个相关联的量,当甲扩大到原来的8倍,乙也随着扩大到原来的8倍时,甲与乙成( )比例;当甲扩大到原来的8倍,乙却随着缩小到原来的时,甲与乙成( )比例。
三、判断题
13.六年级二班学生人数一定,出勤人数和出勤率成反比例。( )
14.车轮的直径一定,所行路程与车轮转的周数成正比例。( )
15.运一批货物,所需要的汽车数量和每辆运的吨数成正比例关系。( )
16.因为9×4=12×3,所以9∶4=12∶3。( )
17.如果 =y,那么x和y成正比例.( )(判断对错)
四、计算题
18.求出下面各题中的未知数。
五、解答题
19.水是生命之源,学校对同学们进行了节约用水教育。笑笑测试了一个打开水龙头的出水量,并记录了下表的数据。
时间/秒 0 10 20 30 40 50 …
出水量/L 0 3 6 9 ( ) ( ) …
(1)把上表填写完整。
(2)时间与出水量成正比吗?解释原因。
20.一辆汽车两次行驶的路程与耗油量如下表:
行驶路程/km 24 96
耗油量/L 2 8
(1)分别写出每次行驶路程与耗油量的比值,判断这两个比能否组成比例。
(2)分别写出两次耗油量与对应行驶路程的比值,看看这两个比能否组成比例。
21.一台播种机第一次工作3时,播种17100m2;第二次工作4时,播种22800m2,分别写出每次播种的面积和工作时间的比,你认为它们能组成比例吗?为什么?
22.六年级(1)班同学自愿购买《童话故事》图书的数量与总价的情况如表所示。
数量/本 1 2 3 4 5 6
总价/元 15 30
(1)把上面的表格填写完整。
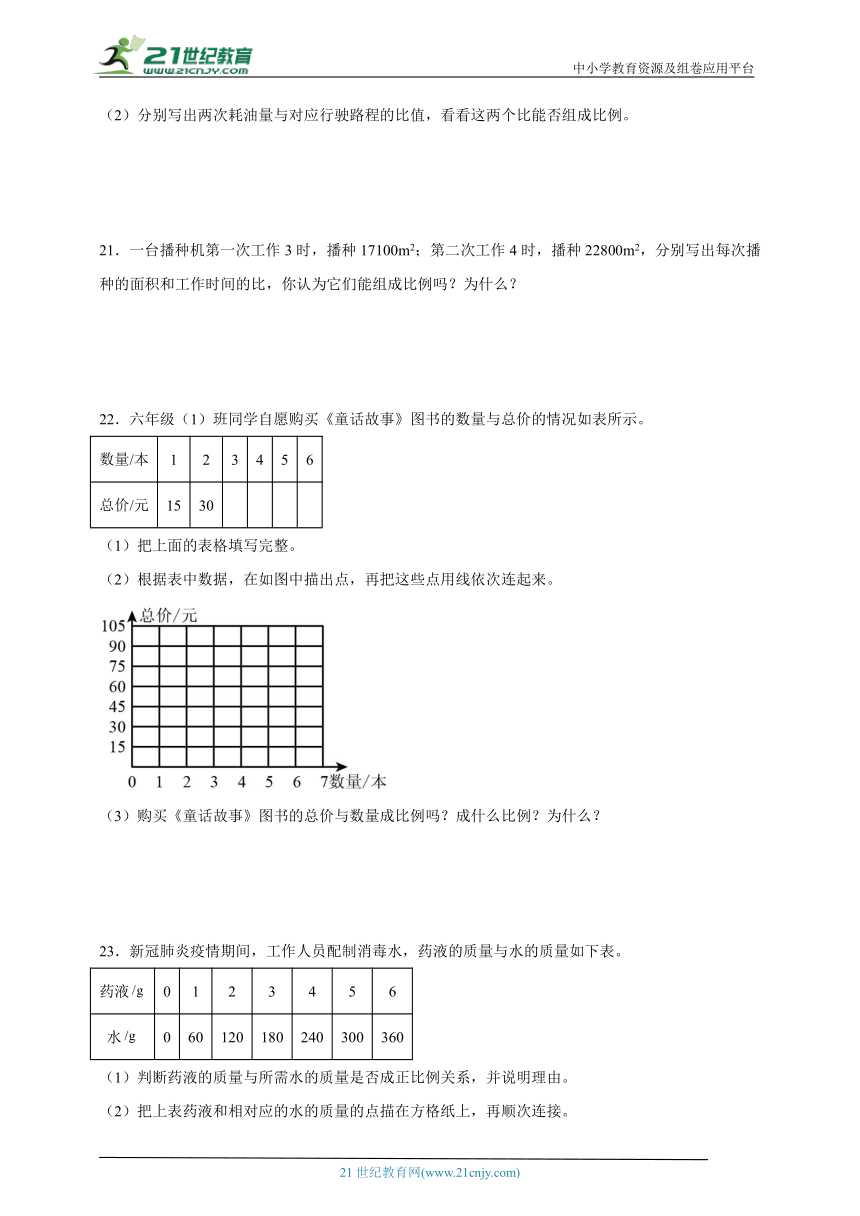
(2)根据表中数据,在如图中描出点,再把这些点用线依次连起来。
(3)购买《童话故事》图书的总价与数量成比例吗?成什么比例?为什么?
23.新冠肺炎疫情期间,工作人员配制消毒水,药液的质量与水的质量如下表。
药液 0 1 2 3 4 5 6
水 0 60 120 180 240 300 360
(1)判断药液的质量与所需水的质量是否成正比例关系,并说明理由。
(2)把上表药液和相对应的水的质量的点描在方格纸上,再顺次连接。
(3)4.5千克药液需要和 ( )千克水配置这种消毒水;水需要和( )药液配置这种消毒水。
参考答案:
1.A
【分析】单价=总钱数÷数量,据此解答。
【详解】总钱数÷袋数=2.5(元),即比值是2.5,比值一定,所以成正比例。
故答案为:A
【点睛】重点考查正比例的定义。
2.C
【解析】根据正、反比例的定义判断。
【详解】卖出的件数+剩下的件数=总件数,总件数一定,即和一定,不成比例。
故答案为:C
【点睛】本题重点考查两个量成正、反比例的判断方法。
3.B
【解析】两个量的比值一定,这两个量成正比例,据此解答。
【详解】A. 圆的半径和周长。=2π比值是一个定值,所以圆的半径和周长成正比例。
B. 正方形的边长和面积。=正方形的边长,不是定值,所以不成比例。
C.=y。=4,即比值一定,成正比例。
故答案为:B
【点睛】本题重点考查两个量成正比例的判断方法。
4.A
【分析】圆周率是固定的,圆周率的2倍也是一定的,判断圆的周长与半径的商一定还是乘积一定,
如果商一定就成正比例,如果乘积一定就成反比例,否则不成比例。
【详解】根据圆周长公式可知:圆的周长÷半径=圆周率的2倍(一定),圆的周长和半径的商一定,二者成正比例。
故答案为:A
5.C
【解析】略
6.C
【解析】略
7.正
【分析】圆柱的高一定,也就是圆柱的侧面积与底面周长的比值一定,,据此解答。
【详解】根据分析可得,圆柱的高一定,圆柱的侧面积和底面周长的比值一定,成(正)比例。
【点睛】本题考查了辨别正、反比例的量,牢记两种相关联的量,积一定为反比例关系,比值一定为正比例关系。
8.正
【分析】做的零件个数=加工的总时间÷做一个零件所用的时间,比值一定,据此解答。
【详解】根据分析可得:做的零件个数一定,做一个零件所用的时间和加工的总时间成(正)比例。
【点睛】本题考查了辨别正、反比例的量,牢记两种相关联的量,积一定为反比例关系,比值一定为正比例关系。
9. 49 48
【分析】因为齿轮的齿数×转数=转过的总齿数(一定),所以齿轮的转数与齿数成反比例;设出未知数,列出比例式解答即可;
【详解】解:设C轮有x个齿,B有y齿轮。
6x=42×7
6x=294
x=49
7y=49×1
y=7
B旋转的圈数:42×8÷7
=336÷7
=48(圈)
【点睛】解答此题的关键:齿轮的齿数×转数=转过的总齿数(一定),齿轮的转数与齿数成反比例。
10.正
【分析】正比例:相关联的两个量,比值一定。反比例:相关联的两个量,乘积一定。据此进行判断。
【详解】因为,所以a=2b。又因为=,所以c=5b。即a÷c=2b÷5b=(比值一定,成正比例)。a×c=2b×5b=10b (乘积不一定,不能成反比例)。综上所述,a和c成正比例。
【点睛】此题属于辨别成正、反比例的量,需熟练掌握正比例和反比例的概念并细心计算才是解题的关键。
11.27
【分析】我们由图可以得知,面积分别为30平方厘米和45平方厘米的长相等,面积分别为30平方厘米和18平方厘米的宽相等。即:对角的两个长方形面积的乘积一定,成反比例。
【详解】第四个小长方形的面积是:
45×18÷30
=810÷30
=27(平方厘米)
【点睛】熟练掌握反比例的知识才是解题的核心。
12. 正 反
【分析】正比例:相关联的两个量,比值一定。反比例:相关联的两个量,乘积一定。据此解答。
【详解】甲、乙是两个相关联的量,当甲扩大到原来的8倍,乙也随着扩大到原来的8倍时,即甲与乙的比值一定,甲与乙成正比例;当甲扩大到原来的8倍,乙却随着缩小到原来的时,即甲与乙的乘积一定,甲与乙成反比例。
【点睛】熟练掌握的正比例和反比例的概念是解题的关键。
13.×
【分析】判断出勤人数和出勤率之间是否成反比例,就看这两个量是否是对应的乘积一定,如果是乘积一定,就成反比例,如果不是乘积一定就不成反比例。
【详解】因为出勤人数÷出勤率=总人数(一定),是出勤人数和出勤率的比值一定,不符合反比例的意义。
所以原题说法错误。
【点睛】此题考查辨识成反比例的量,只要两种相关联的量的乘积一定,就成反比例。
14.√
【分析】因为行驶的路程和转的周数是两种相关联的量,车轮的直径一定,也就是车轮的周长一定,转动周数越多,路程就越长;即所行路程与车轮转动的周数的比值一定。
【详解】由分析可知;车轮的直径一定,所行路程与车轮转的周数成正比例,此说法正确。
故答案为:√
【点睛】此题考查对正比例概念的理解以及判别方法的掌握。
15.×
【分析】根据题意可知,货物的总吨数等于汽车数量乘每辆运的吨数,因此汽车数量和每辆运的吨数是成反比例关系。
【详解】根据分析可知,运一批货物,所需要的汽车数量和每辆运的吨数成反比例关系。
所以原题说法错误。
【点睛】这个题目考查正比例和反比例的认识,两个变量如果可以写成=k(k是不为零的常数),那么y和x成正比例;如果可以写成xy=k(k是不为零的常数),那么y和x成反比例。
16.×
【分析】根据比例的基本性质解答。
【详解】假设9∶4=12∶3,根据比例的基本性质,9×3=4×12。
因为9×3=27,4×12=48,9×3≠4×12,所以9∶4≠12∶3。
故答案为:×
【点睛】比例的基本性质:在比例里,两个外项的积等于两个内项的积。
17.正确
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例.据此解答.
【详解】解: =y,则x:y=7(比值一定),所以x和y成正比例; 故答案为正确.
18.x=11;x=;x=;x=
【分析】2x+2.7=24.7,用24.7-2.7,再用24.7-2.7的差除以2,即可;
x-=,先算出+,再用+的和除以,即可;
=,利用比例的基本性质,原式化为:25x=0.75×8,再用0.75×8的积除以25,即可;
∶=∶x,解比例,原式化为:x=×,再用×的积除以,即可。
【详解】2x+2.7=24.7
解:2x=24.7-2.7
2x=22
x=22÷2
x=11
x-=
解:x=+
x=+
x=
x=÷
x=
=
解:25x=0.75×8
25x=6
x=6÷25
x=
∶=∶x
解:x=×
x=
x=÷
x=×6
x=
19.(1)12;15
(2)成正比例,因为出水量和时间的比值是定值,所以时间和出水量成正比例。
【分析】(1)观察表格可知,时间每增加10秒,出水量就增加3升,据此计算出结果即可;
(2)两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量相对应的两个数的比值(也就是商)一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系;
【详解】(1)9+3=12(升)
12+3=15(升)
所以,时间40秒时,出水量12升;时间50秒时,出水量15升。
(2)3∶10=6∶20=9∶30=
答:时间与出水量成正比,因为出水量和时间的比值是定值,所以时间和出水量成正比例。
【点睛】此题考查了正比例的运用,关键掌握正比例的判断方法。
20.(1)12;12;能组成比例
(2);;能组成比例
【分析】(1)根据题意,先写出两次行驶路程与对应耗油数量的比,然后分别求出比值,通过比较比值判断出两次行驶路程与耗油数量的比能否组成比例。如果比值相等,能组成比例,反之则不能。
(2)先写出两次耗油量与对应两次行驶的路程的比,然后分别求出比值,通过比较比值判断出两次耗油量程与行驶路程的比能否组成比例。如果比值相等,能组成比例,反之则不能。
【详解】(1)行驶路程与耗油数量的比分别是:
24∶2
96∶8
24∶2=12
96∶8=12
12=12
这两个比能成比例
答:这两个比能组成比例。
(2)两次耗油量与对应行驶路程的比分别是:
2∶24
8∶96
2∶24=
8∶96=
=
所以这两个比能组成比例
答:这两个比能组成比例
【点睛】解答此题的关键是明确比例的判定方法,即两个比的比值相同就能组成比例,然后再进一步解答。
21.这两个比能组成比例,因为17100∶3与22800∶4比值相等。
【分析】(1)依据比的意义,分别写出每次播种的面积和工作时间的比。
(2)依据比例的意义,即表示两个比相等的式子,求出两个比的比值,再判断即可。
【详解】第一次播种的面积和工作时间的比17100∶3,第二次播种的面积和工作时间的比22800∶4。
17100∶3=5700∶1=5700
22800∶4=5700∶1=5700
5700=5700
因为17100∶3与22800∶4比值相等,所以这两个比能组成比例,即17100∶3=22800∶4。
【点睛】本题主要考查比的意义以及比例的意义的理解和灵活应用,关键是要掌握比与比例的意义。
22.(1)45;60;75;90
(2)见详解
(3)成比例;成正比例关系;见详解
【分析】(1)从表中的数据可知,1本《童话故事》的价钱是15元;根据“总价=单价×数量”,即可求出买3本、4本、5本、6本《童话故事》的总价,并将表格填写完整。
(2)先根据表中的数据描出各点,然后把各点用线段顺次连接起来即可。
(3)根据正比例的意义:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定(也就是商一定),这两种量成正比例关系。据此解答。
【详解】(1)3×15=45(元)
4×15=60(元)
5×15=75(元)
6×15=90(元)
数量/本 1 2 3 4 5 6
总价/元 15 30 45 60 75 90
(2)如图:
(3)======15(一定)
答:购买《童话故事》图书的总价与数量成比例,成正比例关系。因为=单价(一定),比值一定,所以订阅《童话故事》的总价和数量成正比例关系。
【点睛】本题考查根据信息分析数据的能力,画折线统计图以及正比例关系的辨识。
23.见详解
【分析】(1)根据所需水的质量与药液的质量比,求出比值,再判断即可。
(2)把上表药液和相对应的水的质量的点描在方格纸上,然后再顺次连接各点即可。
(3)根据所需水的质量与药液的比值是60解答即可。
【详解】(1)因为60∶1=120∶2=180∶3=200∶4=300∶5=60(一定),所以药液的质量与所需水的质量成正比例关系。
(2)
(3)(千克)
(克)
4.5千克药液需要和270千克水配置这种消毒水;水需要和药液配置这种消毒水。
【点睛】解答本题关键是明确正比例的意义和辨识成正比例关系的方法。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
常考专题:正比例和反比例(单元测试)-小学数学六年级下册苏教版
一、选择题
1.一袋纯牛奶2.5元,购买纯牛奶的袋数和总钱数( )。
A.成正比例 B.成反比例 C.不成比例
2.张佳的淘宝店儿在“三八节”这天准备了足量的服装,卖出的件数和剩下的件数( )。
A.成正比例 B.成反比例 C.不成比例
3.下面两种相关联的量不成正比例的是( )。
A.圆的半径和周长 B.正方形的边长和面积 C.=y
4.一个圆的半径与周长( )。
A.成正比例 B.成反比例 C.不成比例
5.下面两种相关联的量中,不成比例关系的是( )。
A.平行四边形的面积一定,它的底和高
B.除数一定,被除数和商
C.人的身高和年龄
6.一包薯条,吃掉的数量和余下的数量( )。
A.成正比例 B.成反比例 C.不成比例
二、填空题
7.圆柱的高一定,圆柱的侧面积和底面周长成( )比例。
8.做的零件个数一定,做一个零件所用的时间和加工的总时间成( )比例。
9.A、B、C是三个顺次啮合的齿轮。已知齿轮A旋转7圈时,齿轮C旋转了6圈,如果A的齿数为42,那么C的齿数是( );如果B旋转7圈,C旋转1圈;那么当A旋转8圈时,B旋转( )圈。
10.如果=2,=,其中a,b,c都是大于0的数,那么a和c成( )比例。
11.如图,大长方形被分成了四个小长方形,其实三个小长方形的面积分别为30平方厘米、45平方厘米、18平方厘米,第四个小长方形的面积是( )平方厘米。
12.甲、乙是两个相关联的量,当甲扩大到原来的8倍,乙也随着扩大到原来的8倍时,甲与乙成( )比例;当甲扩大到原来的8倍,乙却随着缩小到原来的时,甲与乙成( )比例。
三、判断题
13.六年级二班学生人数一定,出勤人数和出勤率成反比例。( )
14.车轮的直径一定,所行路程与车轮转的周数成正比例。( )
15.运一批货物,所需要的汽车数量和每辆运的吨数成正比例关系。( )
16.因为9×4=12×3,所以9∶4=12∶3。( )
17.如果 =y,那么x和y成正比例.( )(判断对错)
四、计算题
18.求出下面各题中的未知数。
五、解答题
19.水是生命之源,学校对同学们进行了节约用水教育。笑笑测试了一个打开水龙头的出水量,并记录了下表的数据。
时间/秒 0 10 20 30 40 50 …
出水量/L 0 3 6 9 ( ) ( ) …
(1)把上表填写完整。
(2)时间与出水量成正比吗?解释原因。
20.一辆汽车两次行驶的路程与耗油量如下表:
行驶路程/km 24 96
耗油量/L 2 8
(1)分别写出每次行驶路程与耗油量的比值,判断这两个比能否组成比例。
(2)分别写出两次耗油量与对应行驶路程的比值,看看这两个比能否组成比例。
21.一台播种机第一次工作3时,播种17100m2;第二次工作4时,播种22800m2,分别写出每次播种的面积和工作时间的比,你认为它们能组成比例吗?为什么?
22.六年级(1)班同学自愿购买《童话故事》图书的数量与总价的情况如表所示。
数量/本 1 2 3 4 5 6
总价/元 15 30
(1)把上面的表格填写完整。
(2)根据表中数据,在如图中描出点,再把这些点用线依次连起来。
(3)购买《童话故事》图书的总价与数量成比例吗?成什么比例?为什么?
23.新冠肺炎疫情期间,工作人员配制消毒水,药液的质量与水的质量如下表。
药液 0 1 2 3 4 5 6
水 0 60 120 180 240 300 360
(1)判断药液的质量与所需水的质量是否成正比例关系,并说明理由。
(2)把上表药液和相对应的水的质量的点描在方格纸上,再顺次连接。
(3)4.5千克药液需要和 ( )千克水配置这种消毒水;水需要和( )药液配置这种消毒水。
参考答案:
1.A
【分析】单价=总钱数÷数量,据此解答。
【详解】总钱数÷袋数=2.5(元),即比值是2.5,比值一定,所以成正比例。
故答案为:A
【点睛】重点考查正比例的定义。
2.C
【解析】根据正、反比例的定义判断。
【详解】卖出的件数+剩下的件数=总件数,总件数一定,即和一定,不成比例。
故答案为:C
【点睛】本题重点考查两个量成正、反比例的判断方法。
3.B
【解析】两个量的比值一定,这两个量成正比例,据此解答。
【详解】A. 圆的半径和周长。=2π比值是一个定值,所以圆的半径和周长成正比例。
B. 正方形的边长和面积。=正方形的边长,不是定值,所以不成比例。
C.=y。=4,即比值一定,成正比例。
故答案为:B
【点睛】本题重点考查两个量成正比例的判断方法。
4.A
【分析】圆周率是固定的,圆周率的2倍也是一定的,判断圆的周长与半径的商一定还是乘积一定,
如果商一定就成正比例,如果乘积一定就成反比例,否则不成比例。
【详解】根据圆周长公式可知:圆的周长÷半径=圆周率的2倍(一定),圆的周长和半径的商一定,二者成正比例。
故答案为:A
5.C
【解析】略
6.C
【解析】略
7.正
【分析】圆柱的高一定,也就是圆柱的侧面积与底面周长的比值一定,,据此解答。
【详解】根据分析可得,圆柱的高一定,圆柱的侧面积和底面周长的比值一定,成(正)比例。
【点睛】本题考查了辨别正、反比例的量,牢记两种相关联的量,积一定为反比例关系,比值一定为正比例关系。
8.正
【分析】做的零件个数=加工的总时间÷做一个零件所用的时间,比值一定,据此解答。
【详解】根据分析可得:做的零件个数一定,做一个零件所用的时间和加工的总时间成(正)比例。
【点睛】本题考查了辨别正、反比例的量,牢记两种相关联的量,积一定为反比例关系,比值一定为正比例关系。
9. 49 48
【分析】因为齿轮的齿数×转数=转过的总齿数(一定),所以齿轮的转数与齿数成反比例;设出未知数,列出比例式解答即可;
【详解】解:设C轮有x个齿,B有y齿轮。
6x=42×7
6x=294
x=49
7y=49×1
y=7
B旋转的圈数:42×8÷7
=336÷7
=48(圈)
【点睛】解答此题的关键:齿轮的齿数×转数=转过的总齿数(一定),齿轮的转数与齿数成反比例。
10.正
【分析】正比例:相关联的两个量,比值一定。反比例:相关联的两个量,乘积一定。据此进行判断。
【详解】因为,所以a=2b。又因为=,所以c=5b。即a÷c=2b÷5b=(比值一定,成正比例)。a×c=2b×5b=10b (乘积不一定,不能成反比例)。综上所述,a和c成正比例。
【点睛】此题属于辨别成正、反比例的量,需熟练掌握正比例和反比例的概念并细心计算才是解题的关键。
11.27
【分析】我们由图可以得知,面积分别为30平方厘米和45平方厘米的长相等,面积分别为30平方厘米和18平方厘米的宽相等。即:对角的两个长方形面积的乘积一定,成反比例。
【详解】第四个小长方形的面积是:
45×18÷30
=810÷30
=27(平方厘米)
【点睛】熟练掌握反比例的知识才是解题的核心。
12. 正 反
【分析】正比例:相关联的两个量,比值一定。反比例:相关联的两个量,乘积一定。据此解答。
【详解】甲、乙是两个相关联的量,当甲扩大到原来的8倍,乙也随着扩大到原来的8倍时,即甲与乙的比值一定,甲与乙成正比例;当甲扩大到原来的8倍,乙却随着缩小到原来的时,即甲与乙的乘积一定,甲与乙成反比例。
【点睛】熟练掌握的正比例和反比例的概念是解题的关键。
13.×
【分析】判断出勤人数和出勤率之间是否成反比例,就看这两个量是否是对应的乘积一定,如果是乘积一定,就成反比例,如果不是乘积一定就不成反比例。
【详解】因为出勤人数÷出勤率=总人数(一定),是出勤人数和出勤率的比值一定,不符合反比例的意义。
所以原题说法错误。
【点睛】此题考查辨识成反比例的量,只要两种相关联的量的乘积一定,就成反比例。
14.√
【分析】因为行驶的路程和转的周数是两种相关联的量,车轮的直径一定,也就是车轮的周长一定,转动周数越多,路程就越长;即所行路程与车轮转动的周数的比值一定。
【详解】由分析可知;车轮的直径一定,所行路程与车轮转的周数成正比例,此说法正确。
故答案为:√
【点睛】此题考查对正比例概念的理解以及判别方法的掌握。
15.×
【分析】根据题意可知,货物的总吨数等于汽车数量乘每辆运的吨数,因此汽车数量和每辆运的吨数是成反比例关系。
【详解】根据分析可知,运一批货物,所需要的汽车数量和每辆运的吨数成反比例关系。
所以原题说法错误。
【点睛】这个题目考查正比例和反比例的认识,两个变量如果可以写成=k(k是不为零的常数),那么y和x成正比例;如果可以写成xy=k(k是不为零的常数),那么y和x成反比例。
16.×
【分析】根据比例的基本性质解答。
【详解】假设9∶4=12∶3,根据比例的基本性质,9×3=4×12。
因为9×3=27,4×12=48,9×3≠4×12,所以9∶4≠12∶3。
故答案为:×
【点睛】比例的基本性质:在比例里,两个外项的积等于两个内项的积。
17.正确
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例.据此解答.
【详解】解: =y,则x:y=7(比值一定),所以x和y成正比例; 故答案为正确.
18.x=11;x=;x=;x=
【分析】2x+2.7=24.7,用24.7-2.7,再用24.7-2.7的差除以2,即可;
x-=,先算出+,再用+的和除以,即可;
=,利用比例的基本性质,原式化为:25x=0.75×8,再用0.75×8的积除以25,即可;
∶=∶x,解比例,原式化为:x=×,再用×的积除以,即可。
【详解】2x+2.7=24.7
解:2x=24.7-2.7
2x=22
x=22÷2
x=11
x-=
解:x=+
x=+
x=
x=÷
x=
=
解:25x=0.75×8
25x=6
x=6÷25
x=
∶=∶x
解:x=×
x=
x=÷
x=×6
x=
19.(1)12;15
(2)成正比例,因为出水量和时间的比值是定值,所以时间和出水量成正比例。
【分析】(1)观察表格可知,时间每增加10秒,出水量就增加3升,据此计算出结果即可;
(2)两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量相对应的两个数的比值(也就是商)一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系;
【详解】(1)9+3=12(升)
12+3=15(升)
所以,时间40秒时,出水量12升;时间50秒时,出水量15升。
(2)3∶10=6∶20=9∶30=
答:时间与出水量成正比,因为出水量和时间的比值是定值,所以时间和出水量成正比例。
【点睛】此题考查了正比例的运用,关键掌握正比例的判断方法。
20.(1)12;12;能组成比例
(2);;能组成比例
【分析】(1)根据题意,先写出两次行驶路程与对应耗油数量的比,然后分别求出比值,通过比较比值判断出两次行驶路程与耗油数量的比能否组成比例。如果比值相等,能组成比例,反之则不能。
(2)先写出两次耗油量与对应两次行驶的路程的比,然后分别求出比值,通过比较比值判断出两次耗油量程与行驶路程的比能否组成比例。如果比值相等,能组成比例,反之则不能。
【详解】(1)行驶路程与耗油数量的比分别是:
24∶2
96∶8
24∶2=12
96∶8=12
12=12
这两个比能成比例
答:这两个比能组成比例。
(2)两次耗油量与对应行驶路程的比分别是:
2∶24
8∶96
2∶24=
8∶96=
=
所以这两个比能组成比例
答:这两个比能组成比例
【点睛】解答此题的关键是明确比例的判定方法,即两个比的比值相同就能组成比例,然后再进一步解答。
21.这两个比能组成比例,因为17100∶3与22800∶4比值相等。
【分析】(1)依据比的意义,分别写出每次播种的面积和工作时间的比。
(2)依据比例的意义,即表示两个比相等的式子,求出两个比的比值,再判断即可。
【详解】第一次播种的面积和工作时间的比17100∶3,第二次播种的面积和工作时间的比22800∶4。
17100∶3=5700∶1=5700
22800∶4=5700∶1=5700
5700=5700
因为17100∶3与22800∶4比值相等,所以这两个比能组成比例,即17100∶3=22800∶4。
【点睛】本题主要考查比的意义以及比例的意义的理解和灵活应用,关键是要掌握比与比例的意义。
22.(1)45;60;75;90
(2)见详解
(3)成比例;成正比例关系;见详解
【分析】(1)从表中的数据可知,1本《童话故事》的价钱是15元;根据“总价=单价×数量”,即可求出买3本、4本、5本、6本《童话故事》的总价,并将表格填写完整。
(2)先根据表中的数据描出各点,然后把各点用线段顺次连接起来即可。
(3)根据正比例的意义:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定(也就是商一定),这两种量成正比例关系。据此解答。
【详解】(1)3×15=45(元)
4×15=60(元)
5×15=75(元)
6×15=90(元)
数量/本 1 2 3 4 5 6
总价/元 15 30 45 60 75 90
(2)如图:
(3)======15(一定)
答:购买《童话故事》图书的总价与数量成比例,成正比例关系。因为=单价(一定),比值一定,所以订阅《童话故事》的总价和数量成正比例关系。
【点睛】本题考查根据信息分析数据的能力,画折线统计图以及正比例关系的辨识。
23.见详解
【分析】(1)根据所需水的质量与药液的质量比,求出比值,再判断即可。
(2)把上表药液和相对应的水的质量的点描在方格纸上,然后再顺次连接各点即可。
(3)根据所需水的质量与药液的比值是60解答即可。
【详解】(1)因为60∶1=120∶2=180∶3=200∶4=300∶5=60(一定),所以药液的质量与所需水的质量成正比例关系。
(2)
(3)(千克)
(克)
4.5千克药液需要和270千克水配置这种消毒水;水需要和药液配置这种消毒水。
【点睛】解答本题关键是明确正比例的意义和辨识成正比例关系的方法。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
