19.1.2 第2课时 函数的表示法 课件(20张PPT)【2023春人教版八下数学优质备课】
文档属性
| 名称 | 19.1.2 第2课时 函数的表示法 课件(20张PPT)【2023春人教版八下数学优质备课】 |  | |
| 格式 | pptx | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-11 10:00:54 | ||
图片预览





文档简介
(共20张PPT)
人教八下数学
同步优质课件
人教版八年级下册
交流预习
2023春人教版八(下)数学同步精品课件
核心素养目标
复习引入
互助探究
例题精讲
跟踪训练
分层提高
课堂小结
知识自测
课后作业
第十九章 一次函数
19.1.2 函数的图像
第2课时 函数的表示法
学会用列表、描点、连线画函数图象;提高识图能力分析函数图象信息能力;
核心素养目标:
学会观察、分析函数图象信息,体会数形结合思想,并利用它解决问题,提高解诀问题能力;
学生在充分经历自学、探究、交流、当堂练习等活动中,获得成功的体验,调动主动学习的积极性,感受数学学习的乐趣
复习引入:
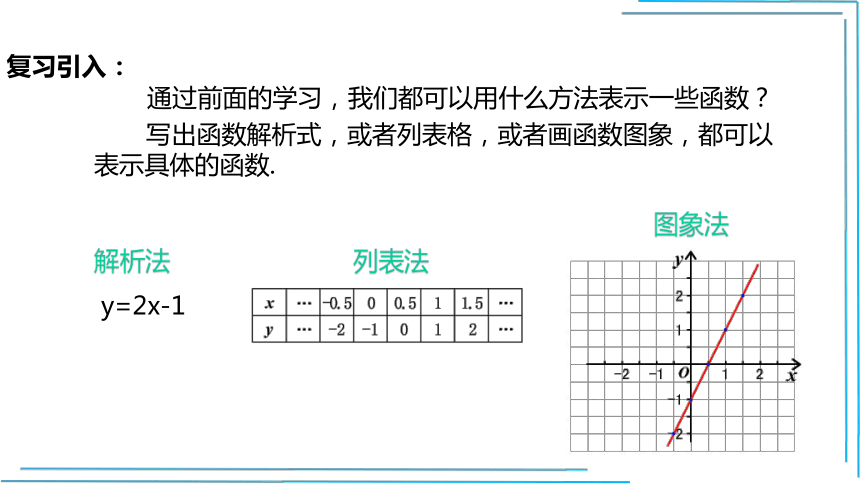
通过前面的学习,我们都可以用什么方法表示一些函数?
写出函数解析式,或者列表格,或者画函数图象,都可以表示具体的函数.
y=2x-1
解析法
列表法
图象法
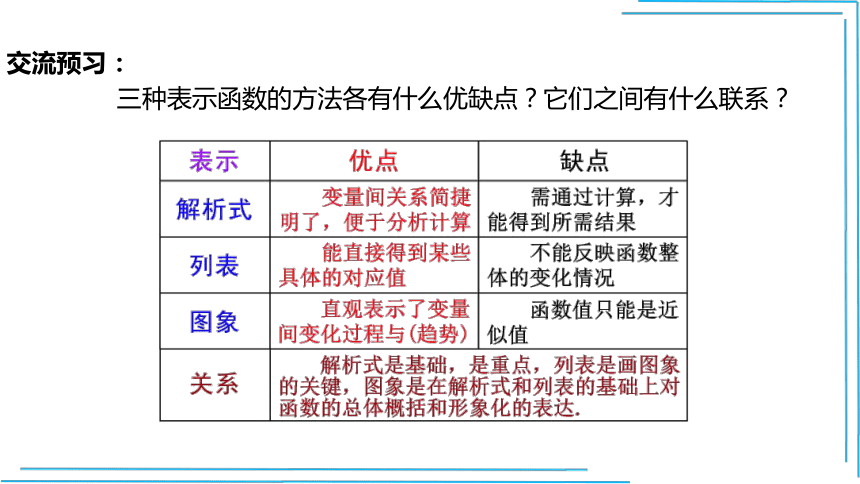
交流预习:
三种表示函数的方法各有什么优缺点?它们之间有什么联系?
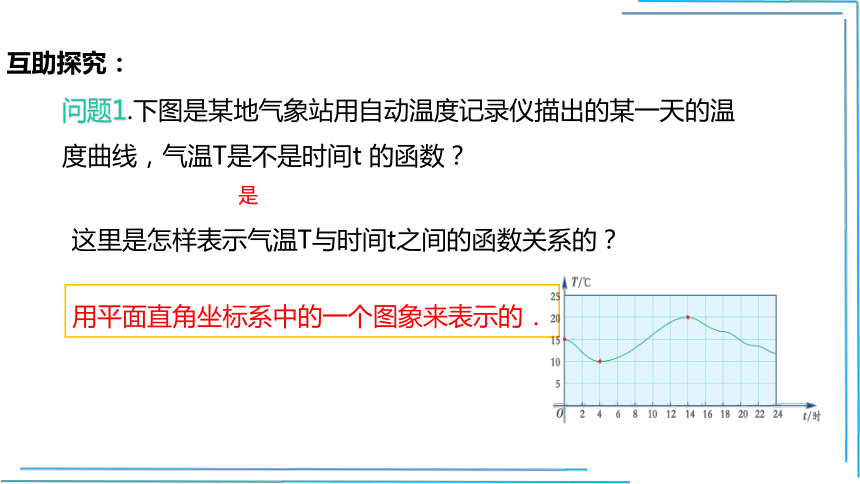
用平面直角坐标系中的一个图象来表示的.
问题1.下图是某地气象站用自动温度记录仪描出的某一天的温度曲线,气温T是不是时间t 的函数?
这里是怎样表示气温T与时间t之间的函数关系的?
是
互助探究:
问题2.正方形的面积S与边长x的取值如下表,S是不是x的函数?
这里是怎样表示正方形面积S与边长x之间的函数关系的?
列表格来表示的.
1 4 9 16 25 36 49
是
互助探究:
问题3.某城市居民用的天然气,1m3收费2.88元,使用x(m3) 天然气应缴纳的费用y(元)为y = 2.88x. y是不是x 的函数?
这里是怎样表示缴纳的天然气费y与所用天然气的体积x的函数关系的?
用函数解析式y=2.88x来表示.
是
互助探究:
例 一水库的水位在最近5 h 内持续上涨,下表记录了这5 h 内6 个时间点的水位高度,其中 t 表示时间,y表示水位高度.
(1)在平面直角坐标系中描出表中数据对应的点,这些点是否在一条直线上?由此你发现水位变化有什么规律?
t/h 0 1 2 3 4 5
y/m 3 3.3 3.6 3.9 4.2 4.5
例题精讲:
x/时
y/米
O
1
2
3
4
5
6
7
8
1
2
3
4
解:可以看出,这6个点 ,且每小时水位
.由此猜想,在这个时间段中水位可能是以
同一速度均匀上升的.
在同一直线上
上升0.3m
5
例题精讲:
(2)水位高度 y 是否为时间 t 的函数?如果是,试写
出一个符合表中数据的函数解析式,并画出函数图象.
这个函数能表示水位的变化规律吗?
(2)由于水位在最近5小时内持续上涨,对于时间t的每一个确定的值,水位高度y 都有 的值与其对应,所以,y t 的函数.
函数解析式为: .
自变量的取值范围是: . 它表示在这 小时内,水位匀速上升的速度为 ,这个函数可以近似地表示水位的变化规律.
唯一
是
y=0.3t+3
0≤t≤5
5
0.3m/h
例题精讲:
(3)据估计这种上涨规律还会持续2 h,预测再过2 h水位高度 将达到多少m.
(3)如果水位的变化规律不变,按上述函数预测,再持续2小时,水位的高度: .
此时函数图象(线段AB)向 延伸到对应的位置,这时水位高度约为 m.
5.1m
右
5.1
例题精讲:
跟踪练习:
1.用列表法与解析式法表示n边形的内角和m(单位:度)关于边数n的函数.
解:列表为:
解析式为:m=180(n-2) (n≥3的整数)
跟踪练习:
2.用解析式法与图象法表示等边三角形的周长 l 关于边长 a 的函数.
解:解析式为:l = 3a (a>0) 图象:如右图所示.
3.一条小船沿直线向码头匀速前进.在0min,2min,4min,6min时,测得小船与码头的距离分别为200m,150m,100m,50m.小船与码头的距离 s 是时间 t 的函数吗?如果是,写出函数解析式,并画出函数图象.如果船速不变,多长时间后小船到达码头?
解:小船与码头的距离 s 是时间 t 的函数,函数解析式为:s =200-25 t (0≤t≤8)其图象是下图中点A(0,200)和点B(8,0)之间的线段AB.如果船速不变,当s =0时,200-25 t =0,解得 t =8,即经过8min后小船到达码头.
跟踪练习:
函数的表示方法
解析式法:反映了函数与自变量之间的数量关系
列表法:反映了函数与自变量的数值对应关系
图象法:反映了函数随自变量的变化而变化的规律
课堂小结:
课后作业:
必做题:81页习题19.1第3、4、5、6、7、8
选做题:83页习题19.1第9、10、11、12、13
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教八下数学
同步优质课件
人教版八年级下册
交流预习
2023春人教版八(下)数学同步精品课件
核心素养目标
复习引入
互助探究
例题精讲
跟踪训练
分层提高
课堂小结
知识自测
课后作业
第十九章 一次函数
19.1.2 函数的图像
第2课时 函数的表示法
学会用列表、描点、连线画函数图象;提高识图能力分析函数图象信息能力;
核心素养目标:
学会观察、分析函数图象信息,体会数形结合思想,并利用它解决问题,提高解诀问题能力;
学生在充分经历自学、探究、交流、当堂练习等活动中,获得成功的体验,调动主动学习的积极性,感受数学学习的乐趣
复习引入:
通过前面的学习,我们都可以用什么方法表示一些函数?
写出函数解析式,或者列表格,或者画函数图象,都可以表示具体的函数.
y=2x-1
解析法
列表法
图象法
交流预习:
三种表示函数的方法各有什么优缺点?它们之间有什么联系?
用平面直角坐标系中的一个图象来表示的.
问题1.下图是某地气象站用自动温度记录仪描出的某一天的温度曲线,气温T是不是时间t 的函数?
这里是怎样表示气温T与时间t之间的函数关系的?
是
互助探究:
问题2.正方形的面积S与边长x的取值如下表,S是不是x的函数?
这里是怎样表示正方形面积S与边长x之间的函数关系的?
列表格来表示的.
1 4 9 16 25 36 49
是
互助探究:
问题3.某城市居民用的天然气,1m3收费2.88元,使用x(m3) 天然气应缴纳的费用y(元)为y = 2.88x. y是不是x 的函数?
这里是怎样表示缴纳的天然气费y与所用天然气的体积x的函数关系的?
用函数解析式y=2.88x来表示.
是
互助探究:
例 一水库的水位在最近5 h 内持续上涨,下表记录了这5 h 内6 个时间点的水位高度,其中 t 表示时间,y表示水位高度.
(1)在平面直角坐标系中描出表中数据对应的点,这些点是否在一条直线上?由此你发现水位变化有什么规律?
t/h 0 1 2 3 4 5
y/m 3 3.3 3.6 3.9 4.2 4.5
例题精讲:
x/时
y/米
O
1
2
3
4
5
6
7
8
1
2
3
4
解:可以看出,这6个点 ,且每小时水位
.由此猜想,在这个时间段中水位可能是以
同一速度均匀上升的.
在同一直线上
上升0.3m
5
例题精讲:
(2)水位高度 y 是否为时间 t 的函数?如果是,试写
出一个符合表中数据的函数解析式,并画出函数图象.
这个函数能表示水位的变化规律吗?
(2)由于水位在最近5小时内持续上涨,对于时间t的每一个确定的值,水位高度y 都有 的值与其对应,所以,y t 的函数.
函数解析式为: .
自变量的取值范围是: . 它表示在这 小时内,水位匀速上升的速度为 ,这个函数可以近似地表示水位的变化规律.
唯一
是
y=0.3t+3
0≤t≤5
5
0.3m/h
例题精讲:
(3)据估计这种上涨规律还会持续2 h,预测再过2 h水位高度 将达到多少m.
(3)如果水位的变化规律不变,按上述函数预测,再持续2小时,水位的高度: .
此时函数图象(线段AB)向 延伸到对应的位置,这时水位高度约为 m.
5.1m
右
5.1
例题精讲:
跟踪练习:
1.用列表法与解析式法表示n边形的内角和m(单位:度)关于边数n的函数.
解:列表为:
解析式为:m=180(n-2) (n≥3的整数)
跟踪练习:
2.用解析式法与图象法表示等边三角形的周长 l 关于边长 a 的函数.
解:解析式为:l = 3a (a>0) 图象:如右图所示.
3.一条小船沿直线向码头匀速前进.在0min,2min,4min,6min时,测得小船与码头的距离分别为200m,150m,100m,50m.小船与码头的距离 s 是时间 t 的函数吗?如果是,写出函数解析式,并画出函数图象.如果船速不变,多长时间后小船到达码头?
解:小船与码头的距离 s 是时间 t 的函数,函数解析式为:s =200-25 t (0≤t≤8)其图象是下图中点A(0,200)和点B(8,0)之间的线段AB.如果船速不变,当s =0时,200-25 t =0,解得 t =8,即经过8min后小船到达码头.
跟踪练习:
函数的表示方法
解析式法:反映了函数与自变量之间的数量关系
列表法:反映了函数与自变量的数值对应关系
图象法:反映了函数随自变量的变化而变化的规律
课堂小结:
课后作业:
必做题:81页习题19.1第3、4、5、6、7、8
选做题:83页习题19.1第9、10、11、12、13
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
