9.1.1不等式及其解集 课件(共19张PPT)
文档属性
| 名称 | 9.1.1不等式及其解集 课件(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 7.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-11 14:01:21 | ||
图片预览



文档简介
(共19张PPT)
9.1.1 不等式及其解集
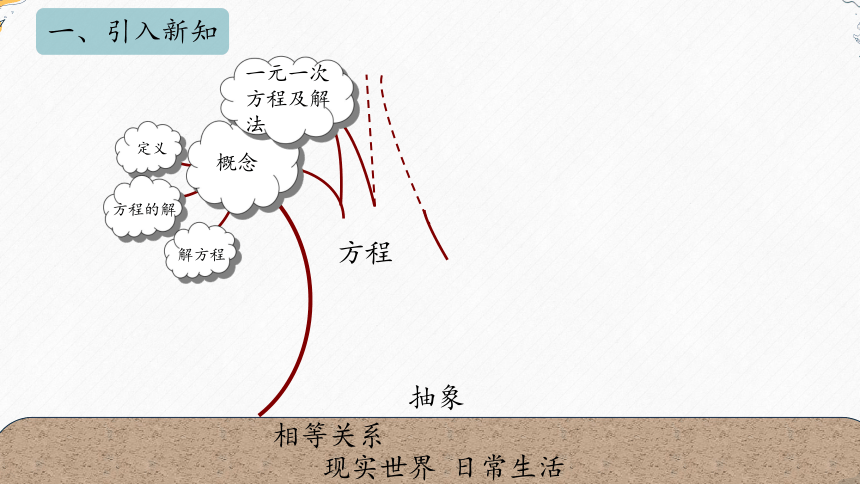
一、引入新知
方程
相等关系
概念
定义
方程的解
解方程
一元一次方程及解法
抽象
现实世界 日常生活
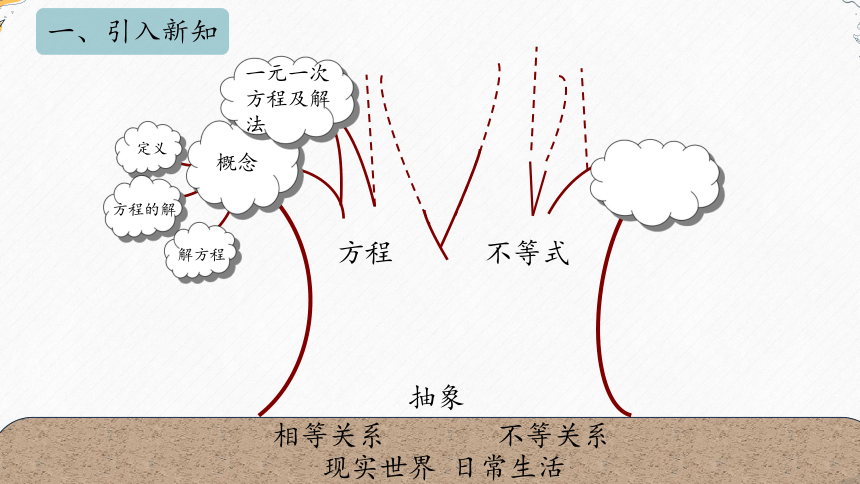
一、引入新知
方程
相等关系
现实世界 日常生活
概念
定义
方程的解
解方程
一元一次方程及解法
抽象
不等关系
不等式
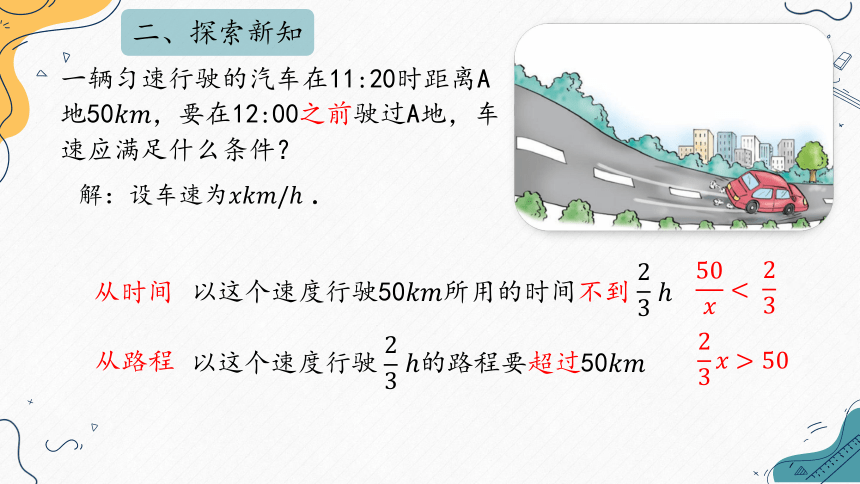
一辆匀速行驶的汽车在11:20时距离A地50,要在12:00之前驶过A地,车速应满足什么条件?
解:设车速为 .
以这个速度行驶 的路程要超过50
以这个速度行驶50所用的时间不到
二、探索新知
从时间
从路程
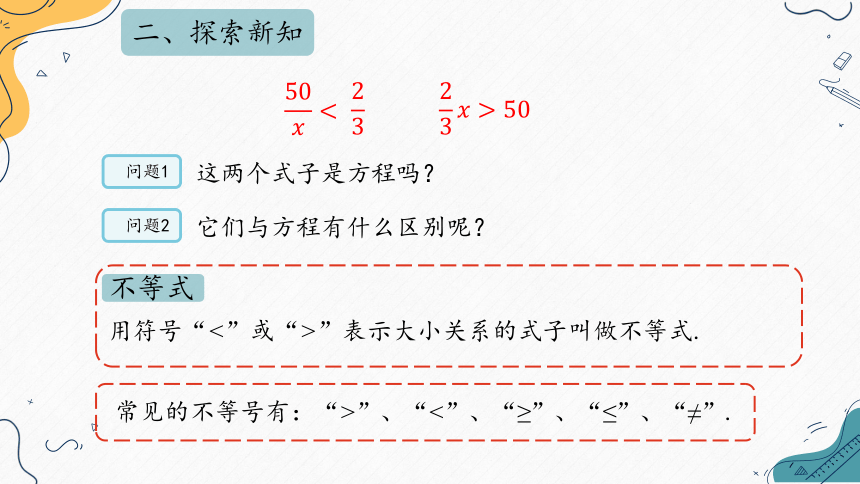
用符号“<”或“>”表示大小关系的式子叫做不等式.
不等式
常见的不等号有:“>”、“<”、“≥”、“≤”、“≠”.
二、探索新知
问题1
这两个式子是方程吗?
问题2
它们与方程有什么区别呢?
(1)3>0; (2)4x+3y≤0;
(3)x=3; (4)x2+xy+y2;
(5)x≠5; (6)x+2≥ y+5.
找不等号.
二、探索新知
巩固1 判断下列式子是不是不等式:
(1)
是正数;
(2)
与5的和小于7;
(3)
与2的差不小于1;
长为 厘米,宽为厘米的长方形的面积不超过10平方厘米;
(4)
(5)
减去3的值不等于2.
找关键词,选不等号,列不等式.
二、探索新知
巩固2 用不等式表示:
不等式:
使不等式成立的未知数的值叫做不等式的解.
不等式的解
二、探索新知
问题1
当车速 是78 时,汽车能在12:00前驶过吗?
问题2
当车速 是72 时,汽车能在12:00前驶过吗?
x=78使不等式成立
x=72使不等式不成立
判断下列数中哪些是不等式 的解.
… 48 60 75 75.3 78 90 …
… …
… …
的解
32
40
50
50.2
52
60
否
否
否
是
是
是
75.3
78
90
问题1
你还能找出这个不等式的其他解吗?
问题2
这个不等式有多少个解?
问题3
这些解应满足什么条件?
无数个
二、探索新知
思考
不等式的解集
是
是
是
一般地,一个含有未知数的不等式的所有的解,组成这个
不等式的解集.
不等式的解集
想一想
不等式的解和不等式的解集一样吗?
不等式的解是对一个数值而言;
不等式的解集是对这些所有的数值的整体而言.
求不等式的解集的过程叫做解不等式.
二、探索新知
(1) x=2是不等式x+3<4的解;
(2)不等式x+1<2的解有无数多个; (3) x=2是不等式3x<7的解集;
(4)2x>4的解集是x>2.
巩固3 判断下列说法是否正确?
二、探索新知
0
2
不等式:
符号
图形
若不包括2这一点,则在该点处画空心圆圈,
画数轴
找界点
定方向
大于向右,
小于向左.
若包括这一点,则在该点处画实心圆点.
二、探索新知
(1) ;
(2) ;
(3) .
解:
;
0
3
解:
;
0
4
解:
.
0
2
二、探索新知
巩固4 直接写出下列不等式的解集,并将其解集表示在数轴上.
三、巩固提升
2.下列各数中,是不等式 +2>4的解的是( )
A.5 B.2 C.0 D.-1
3.不等式x+3>4的解集是( )
A.x>- 1 B.x≥ 1 C.x>3 D.x>1
1.给出下列各式:①-3<0;②a+b;③x xy+y ;④x+2> -7;
⑤a≠3.其中不等式的个数是( )
A.5个 B.2个 C.3个 D.4个
y
-
C
A
D
三、巩固提升
4.用不等式表示:
(1)a与6的和小于5;(2)b的一半大于或等于3;
(3)x与y的和小于0; (4)x与y的差不大于-2.
5.在数轴上表示下列不等式的解集:
(1)x>3; (2)x≤ -2.
解:
0
3
(1)
(2)
0
-2
解:(1)a+6<5;(2) b≥3;(3)x+y<0;(4)x y≤ 2.
-
-
1.本堂课你收获了哪些?
2.你感悟到了哪些数学思想?
3.你还有什么困惑?
四、课堂小结
四、课堂小结
相等关系
不等关系
方程
概念
定义
方程的解
解方程
一元一次方程及解法
抽象
不等式
概念
定义
不等式的解
解不等式
不等式的解集
类比学习
以旧导新
现实世界 日常生活
1. 必做:教材P119-120(习题1、2、3);
2. 选做:类比等式性质,请你自己尝试
探索不等式的性质.
五、课后作业
谢谢
9.1.1 不等式及其解集
一、引入新知
方程
相等关系
概念
定义
方程的解
解方程
一元一次方程及解法
抽象
现实世界 日常生活
一、引入新知
方程
相等关系
现实世界 日常生活
概念
定义
方程的解
解方程
一元一次方程及解法
抽象
不等关系
不等式
一辆匀速行驶的汽车在11:20时距离A地50,要在12:00之前驶过A地,车速应满足什么条件?
解:设车速为 .
以这个速度行驶 的路程要超过50
以这个速度行驶50所用的时间不到
二、探索新知
从时间
从路程
用符号“<”或“>”表示大小关系的式子叫做不等式.
不等式
常见的不等号有:“>”、“<”、“≥”、“≤”、“≠”.
二、探索新知
问题1
这两个式子是方程吗?
问题2
它们与方程有什么区别呢?
(1)3>0; (2)4x+3y≤0;
(3)x=3; (4)x2+xy+y2;
(5)x≠5; (6)x+2≥ y+5.
找不等号.
二、探索新知
巩固1 判断下列式子是不是不等式:
(1)
是正数;
(2)
与5的和小于7;
(3)
与2的差不小于1;
长为 厘米,宽为厘米的长方形的面积不超过10平方厘米;
(4)
(5)
减去3的值不等于2.
找关键词,选不等号,列不等式.
二、探索新知
巩固2 用不等式表示:
不等式:
使不等式成立的未知数的值叫做不等式的解.
不等式的解
二、探索新知
问题1
当车速 是78 时,汽车能在12:00前驶过吗?
问题2
当车速 是72 时,汽车能在12:00前驶过吗?
x=78使不等式成立
x=72使不等式不成立
判断下列数中哪些是不等式 的解.
… 48 60 75 75.3 78 90 …
… …
… …
的解
32
40
50
50.2
52
60
否
否
否
是
是
是
75.3
78
90
问题1
你还能找出这个不等式的其他解吗?
问题2
这个不等式有多少个解?
问题3
这些解应满足什么条件?
无数个
二、探索新知
思考
不等式的解集
是
是
是
一般地,一个含有未知数的不等式的所有的解,组成这个
不等式的解集.
不等式的解集
想一想
不等式的解和不等式的解集一样吗?
不等式的解是对一个数值而言;
不等式的解集是对这些所有的数值的整体而言.
求不等式的解集的过程叫做解不等式.
二、探索新知
(1) x=2是不等式x+3<4的解;
(2)不等式x+1<2的解有无数多个; (3) x=2是不等式3x<7的解集;
(4)2x>4的解集是x>2.
巩固3 判断下列说法是否正确?
二、探索新知
0
2
不等式:
符号
图形
若不包括2这一点,则在该点处画空心圆圈,
画数轴
找界点
定方向
大于向右,
小于向左.
若包括这一点,则在该点处画实心圆点.
二、探索新知
(1) ;
(2) ;
(3) .
解:
;
0
3
解:
;
0
4
解:
.
0
2
二、探索新知
巩固4 直接写出下列不等式的解集,并将其解集表示在数轴上.
三、巩固提升
2.下列各数中,是不等式 +2>4的解的是( )
A.5 B.2 C.0 D.-1
3.不等式x+3>4的解集是( )
A.x>- 1 B.x≥ 1 C.x>3 D.x>1
1.给出下列各式:①-3<0;②a+b;③x xy+y ;④x+2> -7;
⑤a≠3.其中不等式的个数是( )
A.5个 B.2个 C.3个 D.4个
y
-
C
A
D
三、巩固提升
4.用不等式表示:
(1)a与6的和小于5;(2)b的一半大于或等于3;
(3)x与y的和小于0; (4)x与y的差不大于-2.
5.在数轴上表示下列不等式的解集:
(1)x>3; (2)x≤ -2.
解:
0
3
(1)
(2)
0
-2
解:(1)a+6<5;(2) b≥3;(3)x+y<0;(4)x y≤ 2.
-
-
1.本堂课你收获了哪些?
2.你感悟到了哪些数学思想?
3.你还有什么困惑?
四、课堂小结
四、课堂小结
相等关系
不等关系
方程
概念
定义
方程的解
解方程
一元一次方程及解法
抽象
不等式
概念
定义
不等式的解
解不等式
不等式的解集
类比学习
以旧导新
现实世界 日常生活
1. 必做:教材P119-120(习题1、2、3);
2. 选做:类比等式性质,请你自己尝试
探索不等式的性质.
五、课后作业
谢谢
