9.1.1 不等式及其解集 课件(19张PPT)
文档属性
| 名称 | 9.1.1 不等式及其解集 课件(19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-11 15:13:25 | ||
图片预览




文档简介
(共19张PPT)
问题1
A
50千米
11 :20
12 :00
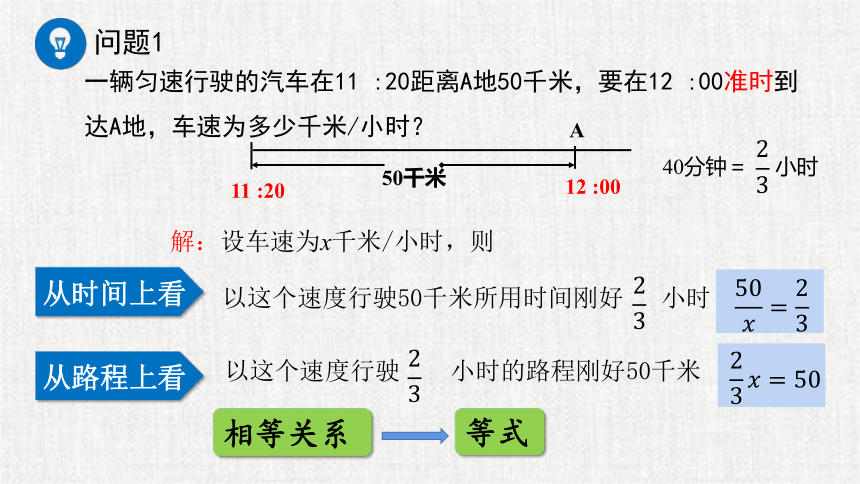
一辆匀速行驶的汽车在11 :20距离A地50千米,要在12 :00准时到达A地,车速为多少千米/小时?
从时间上看
从路程上看
等式
相等关系
以这个速度行驶50千米所用时间刚好 小时
以这个速度行驶 小时的路程刚好50千米
解:设车速为x千米/小时,则
40分钟= 小时
谁大谁小
谁长谁短
谁快谁慢
谁重谁轻
思考:生活中只有相等关系吗?
说一说:你还能举出生活中的哪些不等关系呢
思考:生活中的不等关系又该如何表示
9.1.1不等式及其解集
问题2
不等关系
不等式
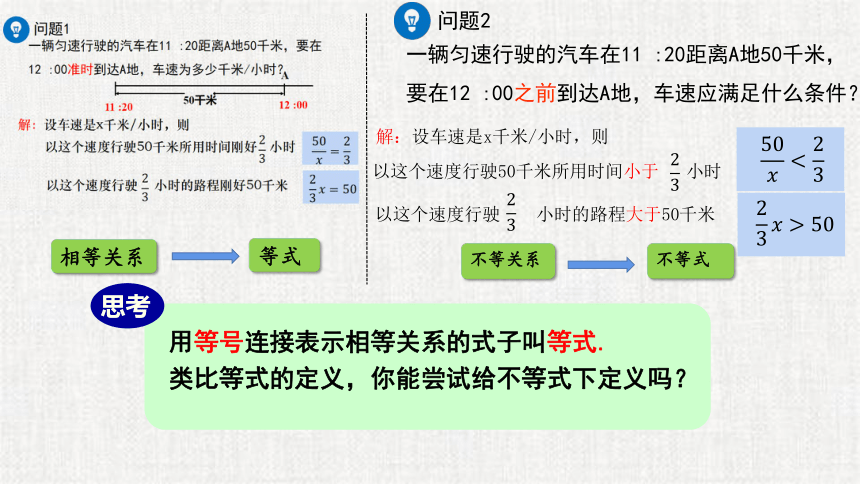
一辆匀速行驶的汽车在11 :20距离A地50千米,要在12 :00之前到达A地,车速应满足什么条件?
用等号连接表示相等关系的式子叫等式.
类比等式的定义,你能尝试给不等式下定义吗?
思考
相等关系
等式
以这个速度行驶50千米所用时间小于 小时
以这个速度行驶 小时的路程大于50千米
解:设车速是x千米/小时,则
不等式的定义
像,用符号“<”或 “>”表示大小关系的式子,叫做不等式.
(1)a是正数; (2)a是负数; (3)a与5的和小于7;
(4)a与2的差大于-1;(5)a的4倍大于8; (6)a的一半小于3;
(7)a与5的和不小于7; (8)a与2的差不大于-1.
练习1.用不等式表示下列关系:
学以致用
a>0;
a+5<7;
a<0;
a – 2>– 1 ;
4a>8;
a<3.
a+5≥7;
a – 2≤ – 1;
练习2.判断下列式子是否是不等式:
(1)3>0; (2)3x– 5≥0; (3)4x+3y≤0;
(4)x=3; (5) x2+xy+y2; (6)x≠5; .
学以致用
是
是
是
不是
不是
是
不等式的定义
像,用符号“<”或 “>”表示大小关系的式子,叫做不等式.
常见的不等号:<、>、≥、≤、≠
解:设车速是x千米/小时,则
问题2
以这个速度行驶50千米所用时间小于小时
以这个速度行驶的路程大于50千米
不等关系
不等式
一辆匀速行驶的汽车在11 :20距离A地50千米,要在12 :00之前到达A地,车速应满足什么条件?
x取哪些值呢?
方程的解
x=78 ?
x=80 ?
使方程两边成立的未知数的值叫做方程的解.
不等式的解
相等关系
等式
使不等式成立的未知数的值叫做不等式的解.
x=78
x=80
x=75
不等式的定义
像,用等号“<”或 “>”表示大小
关系的式子,叫做不等式.
不等式的解
使不等式成立的未知数的值叫做不等式的解.
知识精讲
小组合作
1、除了78和80,不等式 还有其他解吗?
2、如果有,共有几个?
3、这些解应满足什么条件?
不等式的定义
像,用等号“<”或 “>”表示大小
关系的式子,叫做不等式.
不等式的解
使不等式成立的未知数的值叫不等式的解.
不等式的解集
一般的,一个含有未知数的不等式的所有的解,组成了
这个不等式的解集.
不等式的解与不等式的解集有什么区别与联系呢?
思考
知识精讲
解不等式
求不等式解集的过程叫做解不等式。.
问题2
以这个速度行驶50千米所用时间小于小时
以这个速度行驶的路程大于50千米
不等关系
不等式
一辆匀速行驶的汽车在11 :20距离A地50千米,要在12 :00之前到达A地,车速应满足什么条件?
方程的解
不等式的解集
0
75
相等关系
等式
数形结合
解:设车速是x千米/小时,则
练习3.下列各数中,哪些是不等式 的解,哪些不是?
-4, -2.5, 0, 1, 2, 2.5, 3, 3.2, 4.8, 8, 12
解 :3.2, 4.8, 8, 12是不等式x+3>6的解
-4,-2.5,0,1,2,2.5,3不是不等式x+3>6的解
学以致用
B. x=3是2x+1>5的唯一解
C. x=3不是2x+1>5的解
D. x=3是2x+1>5的解集
练习4.下列说法正确的是( )
A. x=3是2x+1>5的解
A
学以致用
学以致用
练习5.直接说出下列不等式的解集,并在数轴上表示出来.
(1)x+3>6
(2)2x<8
(3)x-2≥0
x>3
x<4
x≥2
0
3
0
4
0
2
步骤:
第一步:画数轴(注意三要素);
第二步:找界点(注意空实心);
第三步:定方向(大于向右,小于向左).
课堂小结
实际问题
相等关系
方程
一元一次方程
解法
应用
不等关系
不等式
一元一次不等式
解法
应用
类比
不等式的定义
不等式的解
符号
图形
不等式的解集
数形结合
等式的性质
作业布置
必做:1.通过查阅资料了解等号与不等号的来历;
2.课本P119-120习题9.1: 1,2,3
选做:问题2中不等式 和 的解集一样吗?为什么?
问题1
A
50千米
11 :20
12 :00
一辆匀速行驶的汽车在11 :20距离A地50千米,要在12 :00准时到达A地,车速为多少千米/小时?
从时间上看
从路程上看
等式
相等关系
以这个速度行驶50千米所用时间刚好 小时
以这个速度行驶 小时的路程刚好50千米
解:设车速为x千米/小时,则
40分钟= 小时
谁大谁小
谁长谁短
谁快谁慢
谁重谁轻
思考:生活中只有相等关系吗?
说一说:你还能举出生活中的哪些不等关系呢
思考:生活中的不等关系又该如何表示
9.1.1不等式及其解集
问题2
不等关系
不等式
一辆匀速行驶的汽车在11 :20距离A地50千米,要在12 :00之前到达A地,车速应满足什么条件?
用等号连接表示相等关系的式子叫等式.
类比等式的定义,你能尝试给不等式下定义吗?
思考
相等关系
等式
以这个速度行驶50千米所用时间小于 小时
以这个速度行驶 小时的路程大于50千米
解:设车速是x千米/小时,则
不等式的定义
像,用符号“<”或 “>”表示大小关系的式子,叫做不等式.
(1)a是正数; (2)a是负数; (3)a与5的和小于7;
(4)a与2的差大于-1;(5)a的4倍大于8; (6)a的一半小于3;
(7)a与5的和不小于7; (8)a与2的差不大于-1.
练习1.用不等式表示下列关系:
学以致用
a>0;
a+5<7;
a<0;
a – 2>– 1 ;
4a>8;
a<3.
a+5≥7;
a – 2≤ – 1;
练习2.判断下列式子是否是不等式:
(1)3>0; (2)3x– 5≥0; (3)4x+3y≤0;
(4)x=3; (5) x2+xy+y2; (6)x≠5; .
学以致用
是
是
是
不是
不是
是
不等式的定义
像,用符号“<”或 “>”表示大小关系的式子,叫做不等式.
常见的不等号:<、>、≥、≤、≠
解:设车速是x千米/小时,则
问题2
以这个速度行驶50千米所用时间小于小时
以这个速度行驶的路程大于50千米
不等关系
不等式
一辆匀速行驶的汽车在11 :20距离A地50千米,要在12 :00之前到达A地,车速应满足什么条件?
x取哪些值呢?
方程的解
x=78 ?
x=80 ?
使方程两边成立的未知数的值叫做方程的解.
不等式的解
相等关系
等式
使不等式成立的未知数的值叫做不等式的解.
x=78
x=80
x=75
不等式的定义
像,用等号“<”或 “>”表示大小
关系的式子,叫做不等式.
不等式的解
使不等式成立的未知数的值叫做不等式的解.
知识精讲
小组合作
1、除了78和80,不等式 还有其他解吗?
2、如果有,共有几个?
3、这些解应满足什么条件?
不等式的定义
像,用等号“<”或 “>”表示大小
关系的式子,叫做不等式.
不等式的解
使不等式成立的未知数的值叫不等式的解.
不等式的解集
一般的,一个含有未知数的不等式的所有的解,组成了
这个不等式的解集.
不等式的解与不等式的解集有什么区别与联系呢?
思考
知识精讲
解不等式
求不等式解集的过程叫做解不等式。.
问题2
以这个速度行驶50千米所用时间小于小时
以这个速度行驶的路程大于50千米
不等关系
不等式
一辆匀速行驶的汽车在11 :20距离A地50千米,要在12 :00之前到达A地,车速应满足什么条件?
方程的解
不等式的解集
0
75
相等关系
等式
数形结合
解:设车速是x千米/小时,则
练习3.下列各数中,哪些是不等式 的解,哪些不是?
-4, -2.5, 0, 1, 2, 2.5, 3, 3.2, 4.8, 8, 12
解 :3.2, 4.8, 8, 12是不等式x+3>6的解
-4,-2.5,0,1,2,2.5,3不是不等式x+3>6的解
学以致用
B. x=3是2x+1>5的唯一解
C. x=3不是2x+1>5的解
D. x=3是2x+1>5的解集
练习4.下列说法正确的是( )
A. x=3是2x+1>5的解
A
学以致用
学以致用
练习5.直接说出下列不等式的解集,并在数轴上表示出来.
(1)x+3>6
(2)2x<8
(3)x-2≥0
x>3
x<4
x≥2
0
3
0
4
0
2
步骤:
第一步:画数轴(注意三要素);
第二步:找界点(注意空实心);
第三步:定方向(大于向右,小于向左).
课堂小结
实际问题
相等关系
方程
一元一次方程
解法
应用
不等关系
不等式
一元一次不等式
解法
应用
类比
不等式的定义
不等式的解
符号
图形
不等式的解集
数形结合
等式的性质
作业布置
必做:1.通过查阅资料了解等号与不等号的来历;
2.课本P119-120习题9.1: 1,2,3
选做:问题2中不等式 和 的解集一样吗?为什么?
