多面体欧拉公式的发现[上学期]
图片预览






文档简介
课件17张PPT。2019/3/151多面体欧拉公式的发现研究性学习课题;溧水三中 赵婷2019/3/152回顾:
多面体:由若干个平面多边形围成的几何体叫做多面体(polyhedron)在我们生活的现实世界中,就存在着形形色色的多面体,如食盐,明矾,石膏等的晶体都呈现多面体的形状2019/3/1532019/3/1542019/3/155实例:
大家知道C60的分子结构是一个特殊的多面体,科学家是如何构造出这种几何体的?
根据它有60个顶点,从每一个顶点出发有3条棱,即可求出该多面体的面数,再结合各面的形状即可构造出这种多面体。
通过此过程我们猜想多面体的三个元素顶点、面、棱之间可能有什么特殊的关系,请同学们从你熟悉的多面体出发,探究一下它们的关系。
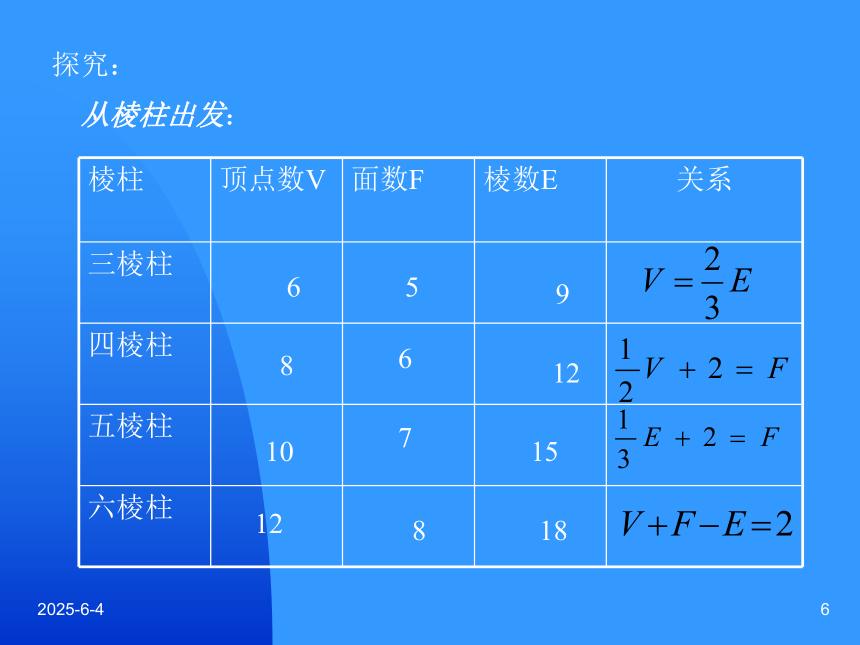
2019/3/156探究:从棱柱出发:659861210715128182019/3/157从棱锥出发:446558661077122019/3/15844655868129916多面体出发;2019/3/1592019/3/15102019/3/1511多面体的顶点数、面数和棱数之间存在规律:
说明:这个结论叫做欧拉定理(其关系式叫做欧拉公式)
问题:是不是所有的多面体都具有这样 的规律?2019/3/1512凹多面体2019/3/15132019/3/15142019/3/1515简单多面体:
如果这些多面体的表面都是用橡皮薄膜制作的,并且可以向它的内部充气,那么表面能变为一个球面的多面体叫做简单多面体。
?
说明:欧拉公式只是适用于简单多面体的棱数、面数、顶点之间的关系2019/3/1516 小 结1、能够认识一些多面体,简单多面体
2、简单多面体欧拉公式的发现与认识2019/3/1517再见
多面体:由若干个平面多边形围成的几何体叫做多面体(polyhedron)在我们生活的现实世界中,就存在着形形色色的多面体,如食盐,明矾,石膏等的晶体都呈现多面体的形状2019/3/1532019/3/1542019/3/155实例:
大家知道C60的分子结构是一个特殊的多面体,科学家是如何构造出这种几何体的?
根据它有60个顶点,从每一个顶点出发有3条棱,即可求出该多面体的面数,再结合各面的形状即可构造出这种多面体。
通过此过程我们猜想多面体的三个元素顶点、面、棱之间可能有什么特殊的关系,请同学们从你熟悉的多面体出发,探究一下它们的关系。
2019/3/156探究:从棱柱出发:659861210715128182019/3/157从棱锥出发:446558661077122019/3/15844655868129916多面体出发;2019/3/1592019/3/15102019/3/1511多面体的顶点数、面数和棱数之间存在规律:
说明:这个结论叫做欧拉定理(其关系式叫做欧拉公式)
问题:是不是所有的多面体都具有这样 的规律?2019/3/1512凹多面体2019/3/15132019/3/15142019/3/1515简单多面体:
如果这些多面体的表面都是用橡皮薄膜制作的,并且可以向它的内部充气,那么表面能变为一个球面的多面体叫做简单多面体。
?
说明:欧拉公式只是适用于简单多面体的棱数、面数、顶点之间的关系2019/3/1516 小 结1、能够认识一些多面体,简单多面体
2、简单多面体欧拉公式的发现与认识2019/3/1517再见
