2014快乐暑假初二升初三衔接——三角形全等(含答案)
文档属性
| 名称 | 2014快乐暑假初二升初三衔接——三角形全等(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 240.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-07-12 17:30:35 | ||
图片预览


文档简介
2014快乐暑假初二升初三衔接——三角形全等
一、知识梳理
1、 的两个三角形全等。即 。
2、 的两个三角形全等。即 。
3、 的两个三角形全等。即 。
4、 的两个三角形全等。即 。
5、 的两个三角形全等。即 。
6、全等三角形的 相等, 相等。证明两条线段(或两个角)相等,可以通过证明其所在的两个三角形 。
二、典例精析
1、(2013 舟山)如图,△ABC与△D ( http: / / www.21cnjy.com )CB中,AC与BD交于点E,且∠A=∠D,AB=DC.
(1)求证:△ABE≌DCE;
(2)当∠AEB=50°,求∠EBC的度数?
HYPERLINK "http://www.21cnjy.com"
2、(2013 珠海)如图,已知,EC=AC,∠BCE=∠DCA,∠A=∠E;求证:BC=DC.
HYPERLINK "http://www.21cnjy.com"
三、巩固提升
3.(2013 安顺)如图,已知AE=CF,∠AFD=∠CEB,那么添加下列一个条件后,仍无法判定△ADF≌△CBE的是( )
A. ∠A=∠C B. AD=CB C. BE=DF D. AD∥BC
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(3) (4) (5)
4.(2012 贵阳)如图,已知点A、D、 ( http: / / www.21cnjy.com )C、F在同一条直线上,AB=DE,BC=EF,要使△ABC≌△DEF,还需要添加一个条件是( )
A. ∠BCA=∠F B. ∠B=∠E C. BC∥EF D. ∠A=∠EDF
5.(2013 铁岭)如图,在△ABC和△DEC中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,不能添加的一组条件是( )
A. BC=EC,∠B=∠E B.BC=EC,AC=DC
C. BC=DC,∠A=∠D D.∠B=∠E,∠A=∠D
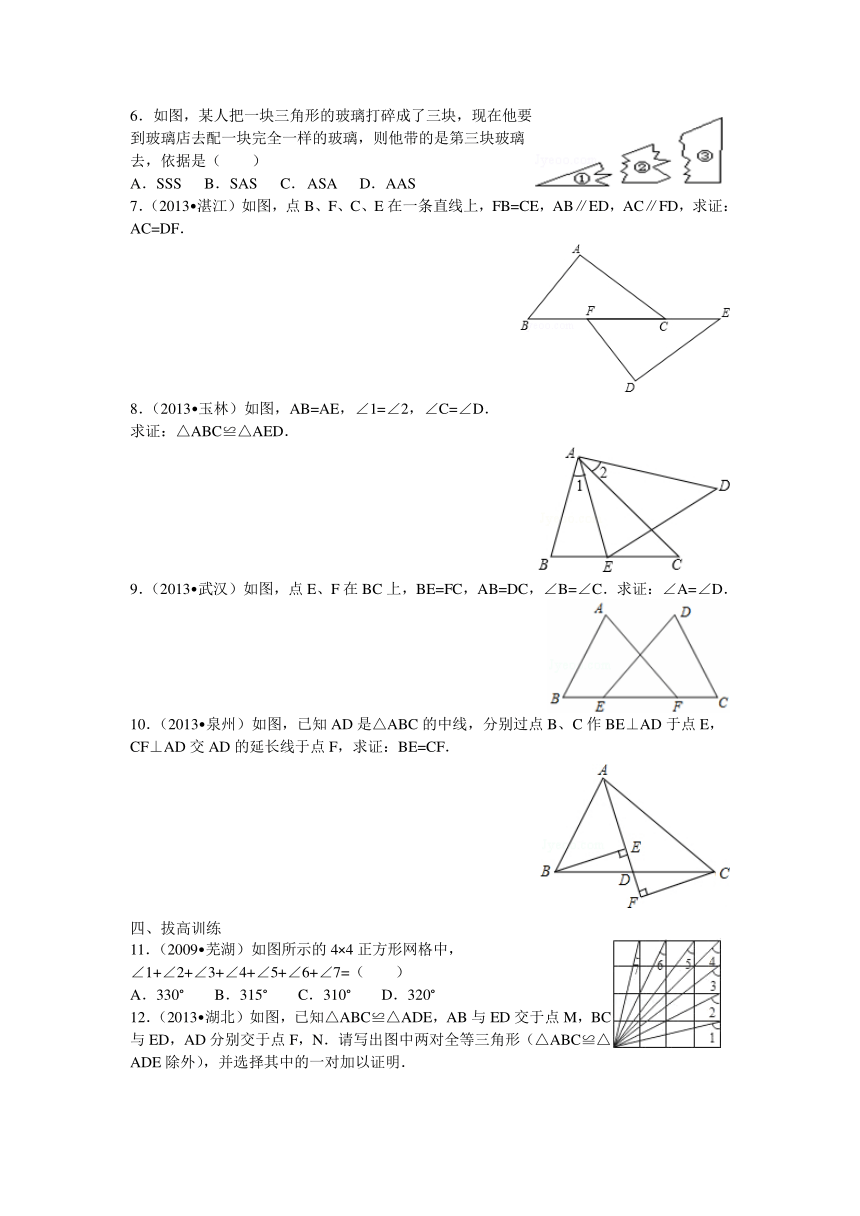
6.如图,某人把一块三角形的玻璃打碎成了三块,现在他要到玻璃店去配一块完全一样的玻璃,则他带的是第三块玻璃去,依据是( )
A.SSS B.SAS C. ASA D.AAS
7.(2013 湛江)如图,点B、F、C、E在一条直线上,FB=CE,AB∥ED,AC∥FD,求证:AC=DF.
( http: / / www.21cnjy.com )
8.(2013 玉林)如图,AB=AE,∠1=∠2,∠C=∠D.
求证:△ABC≌△AED.
( http: / / www.21cnjy.com )
9.(2013 武汉)如图,点E、F在BC上,BE=FC,AB=DC,∠B=∠C.求证:∠A=∠D.
( http: / / www.21cnjy.com )
10.(2013 泉州)如 ( http: / / www.21cnjy.com )图,已知AD是△ABC的中线,分别过点B、C作BE⊥AD于点E,CF⊥AD交AD的延长线于点F,求证:BE=CF.
( http: / / www.21cnjy.com )
四、拔高训练
11.(2009 芜湖)如图所示的4×4正方形网格中,
∠1+∠2+∠3+∠4+∠5+∠6+∠7=( )
A.330° B.315° C.310° D.320°
12.(2013 湖北)如图,已知△A ( http: / / www.21cnjy.com )BC≌△ADE,AB与ED交于点M,BC与ED,AD分别交于点F,N.请写出图中两对全等三角形(△ABC≌△ADE除外),并选择其中的一对加以证明.
( http: / / www.21cnjy.com )
13.(2013 大庆)如图,把一 ( http: / / www.21cnjy.com )个直角三角形ACB(∠ACB=90°)绕着顶点B顺时针旋转60°,使得点C旋转到AB边上的一点D,点A旋转到点E的位置.F,G分别是BD,BE上的点,BF=BG,延长CF与DG交于点H.
(1)求证:CF=DG;
(2)求出∠FHG的度数.
( http: / / www.21cnjy.com )
14.已知,如图,AB、CD相交于点O,AC∥DB,AO=BO,E、F分别是OC、OD中点.
求证:(1)OC=OD;
(2)求证:AE∥BF.
( http: / / www.21cnjy.com )
15.如图,点M、N分别在正三角形ABC的BC、CA边上,且BM=CN,AM、BN交于点Q,求∠AQN的度数.
( http: / / www.21cnjy.com )
16.(2012 镇江)如图,在四 ( http: / / www.21cnjy.com )边形ABCD中,AD∥BC,E是AB的中点,连接DE并延长交CB的延长线于点F,点G在边BC上,且∠GDF=∠ADF.
(1)求证:△ADE≌△BFE;
(2)连接EG,判断EG与DF的位置关系并说明理由.
( http: / / www.21cnjy.com )
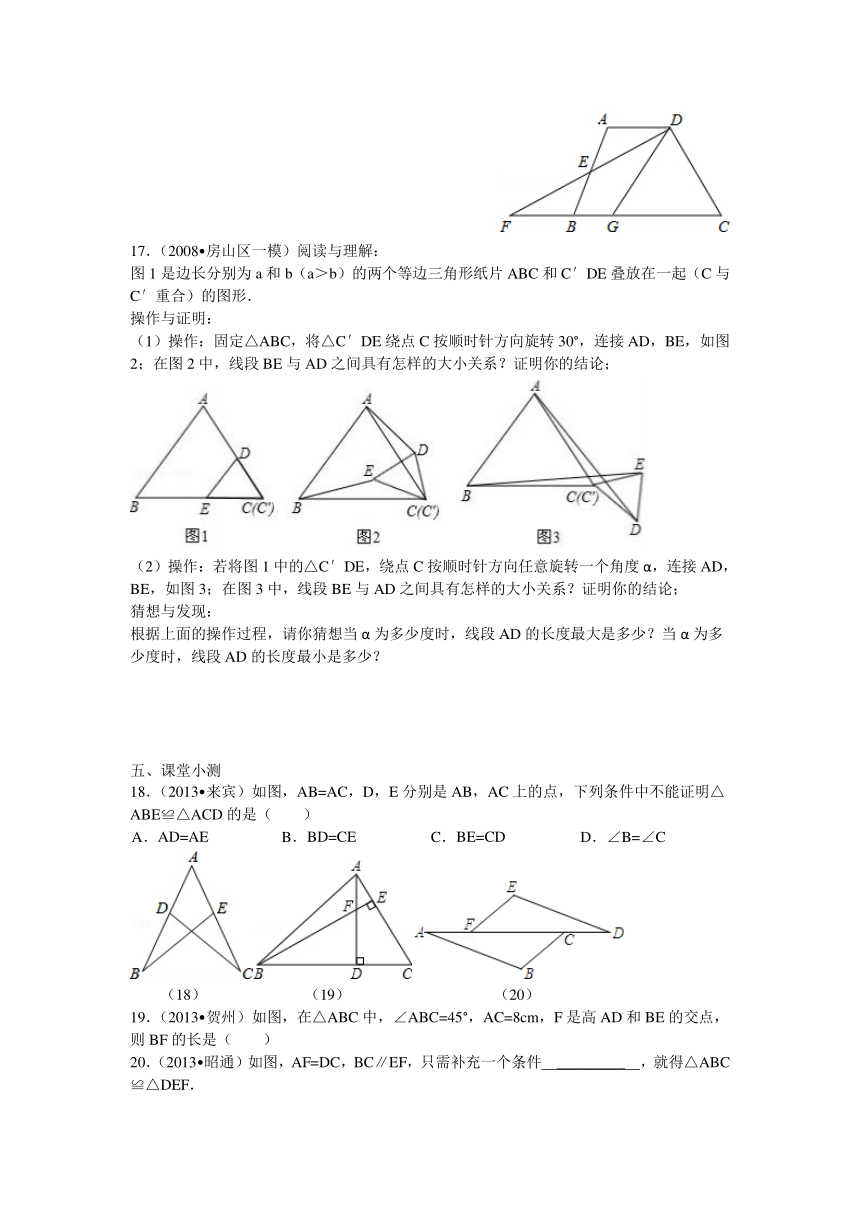
17.(2008 房山区一模)阅读与理解:
图1是边长分别为a和b(a>b)的两个等边三角形纸片ABC和C′DE叠放在一起(C与C′重合)的图形.
操作与证明:
(1)操作:固定△ABC,将△C′DE绕点C ( http: / / www.21cnjy.com )按顺时针方向旋转30°,连接AD,BE,如图2;在图2中,线段BE与AD之间具有怎样的大小关系?证明你的结论;
( http: / / www.21cnjy.com )
(2)操作:若将图1中的△ ( http: / / www.21cnjy.com )C′DE,绕点C按顺时针方向任意旋转一个角度α,连接AD,BE,如图3;在图3中,线段BE与AD之间具有怎样的大小关系?证明你的结论;
猜想与发现:
根据上面的操作过程,请你猜想当α为多少度时,线段AD的长度最大是多少?当α为多少度时,线段AD的长度最小是多少?
五、课堂小测
18.(2013 来宾)如图,AB=AC,D,E分别是AB,AC上的点,下列条件中不能证明△ABE≌△ACD的是( )
A. AD=AE B. BD=CE C. BE=CD D. ∠B=∠C
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(18) (19) (20)
19.(2013 贺州)如图,在△ABC中,∠ABC=45°,AC=8cm,F是高AD和BE的交点,则BF的长是( )
20.(2013 昭通)如图,AF=DC,BC∥EF,只需补充一个条件 _________ ,就得△ABC≌△DEF.
21.(2013 义乌市 ( http: / / www.21cnjy.com ))如图,已知∠B=∠C,添加一个条件使△ABD≌△ACE(不标注新的字母,不添加新的线段),你添加的条件是 _________ .
22(2013 呼和浩特)如图,CD=CA,∠1=∠2,EC=BC,求证:DE=AB.
( http: / / www.21cnjy.com )
23(2012 重庆)已知:如图,AB=AE,∠1=∠2,∠B=∠E.求证:BC=ED.
( http: / / www.21cnjy.com )
六、体验中考
24、(2014年泰安)在△ABC和△A1B1C1中,下列四个命题:
(1)若AB=A1B1,AC=A1C1,∠A=∠A1,则△ABC≌△A1B1C1;
(2)若AB=A1B1,AC=A1C1,∠B=∠B1,则△ABC≌△A1B1C1;
(3)若∠A=∠A1,∠C=∠C1,则△ABC∽△A1B1C1;
(4)若AC:A1C1=CB:C1B1,∠C=∠C1,则△ABC∽△A1B1C1.
其中真命题的个数为( )
A.4个 B. 3个 C. 2个 D. 1个
25、(2014年泰安)将两个斜边长相 ( http: / / www.21cnjy.com )等的三角形纸片如图①放置,其中∠ACB=∠CED=90°,∠A=45°,∠D=30°.把△DCE绕点C顺时针旋转15°得到△D1CE1,如图②,连接D1B,则∠E1D1B的度数为( )
A.10° B. 20° C. 7.5° D. 15°
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(24) (25)
26、2012 泰安)如图,AB∥CD,E,F分别为AC,BD的中点,若AB=5,CD=3,则EF的长是( )
A. 4 B. 3 C. 2 D. 1
27、(2014年泰安)如图,∠ABC ( http: / / www.21cnjy.com )=90°,D、E分别在BC、AC上,AD⊥DE,且AD=DE,点F是AE的中点,FD与AB相交于点M.
(1)求证:∠FMC=∠FCM;
(2)AD与MC垂直吗?并说明理由.
( http: / / www.21cnjy.com )
28、(2013 泰安)如图,在四边形ABCD中,AB=AD,CB=CD,E是CD上一点,BE交AC于F,连接DF.
(1)证明:∠BAC=∠DAC,∠AFD=∠CFE.
( http: / / www.21cnjy.com )
29、(2011 泰安)已知:在△ABC中,AC=BC,∠ACB=90°,点D是AB的中点,点E是AB边上一点.
(1)直线BF垂直于直线CE于点F,交CD于点G(如图1),求证:AE=CG;
(2)直线AH垂直于直线CE,垂足为点H,交CD的延长线于点M(如图2),找出图中与BE相等的线段,并证明.
( http: / / www.21cnjy.com )
2014快乐暑假初二升初三衔接——三角形全等参考答案
1、证明:(1)∵在△ABE和△DCE中
∠A=∠D;∠AEB=∠DEC ;AB=DC
∴△ABE≌△DCE(AAS);
( http: / / www.21cnjy.com )解:(2)∵△ABE≌△DCE,∴BE=EC,
∴∠EBC=∠ECB,
∵∠EBC+∠ECB=∠AEB=50°,
∴∠EBC=25°.
2、证明:∵∠BCE=∠DCA,
∴∠BCE+∠ACE=∠DCA+∠ACE,即∠ACB=∠ECD,
在△ABC和△EDC中,
∠ACB=∠ECD,EC=AC;∠A=∠E
∴△ABC≌△EDC(ASA),∴BC=DC.
3.B.4.B.5.C.6.C.
7.证明:∵FB=CE,∴FB+FC=CE+FC,∴BC=EF,
∵AB∥ED,AC∥FD,∴∠B=∠E,∠ACB=∠DFE,
∵在△ABC和△DEF中,,∴△ABC≌△DEF(ASA),∴AC=DF.
8.证明:∵∠1=∠2,∴∠1+∠EAC=∠2+∠EAC,即∠BAC=∠EAD,
∵在△ABC和△AED中,,∴△ABC≌△AED(AAS).
9.证明:∵BE=FC,∴BE+EF=CF+EF,即BF=CE;
又∵AB=DC,∠B=∠C,∴△ABF≌△DCE;(SAS)∴∠A=∠D.
10.证明:∵AD是△ABC的中线,∴BD=CD,
∵BE⊥AD,CF⊥AD,∴∠BED=∠CFD=90°,
在△BDE和△CDF中,,∴△BDE≌△CDF(AAS),∴BE=CF.
11.B.
12.解:△AEM≌△ACN,△BMF≌△DNF,△ABN≌△ADM.
选择△AEM≌△ACN,理由如下:
∵△ADE≌△ABC,∴AE=AC,∠E=∠C,∠EAD=∠CAB,
∴∠EAM=∠CAN,
∵在△AEM和△ACN中,∴△AEM≌△ACN(ASA).
13.(1)证明:∵在△CBF和△DBG中,
,∴△CBF≌△DBG(SAS),∴CF=DG;
(2)解:∵△CBF≌△DBG,∴∠BCF=∠BDG,
又∵∠CFB=∠DFH,∴∠DHF=∠CBF=60°,
∴∠FHG=180°﹣∠DHF=180°﹣60°=120°.
14.证明:(1)∵AC∥BD,∴∠C=∠D,∠CAO=∠DBO,AO=BO,
∴△AOC≌△BOD,∴CO=DO;
(2)∵E、F分别是OC、OD的中点,∴OF=OD=OC=OE,
由AO=BO,EO=FO,
∴四边形AFBE是平行四边形,
∴AE∥BF.(其他方法:证明全等,在证明内错角相等也可)
15.解:∵BM=CN∴CM=AN,
又∵AB=AC,∠BAN=∠ACM,
∴△AMC≌△BNA,则∠BNA=∠AMC,
∵∠MAN+∠ANB+∠AQN=180°
∠MAN+∠AMC+∠ACB=180°,
∴∠AQN=∠ACB=60°.
16.(1)证明:∵AD∥BC,∴∠ADE=∠BFE,
∵E为AB的中点,∴AE=BE,
在△AED和△BFE中,,∴△AED≌△BFE(AAS);
(2)解:EG与DF的位置关系是EG垂直平分DF,理由为:连接EG,
∵∠GDF=∠ADE,∠ADE=∠BFE,
∴∠GDF=∠BFE,
由(1)△AED≌△BFE得:DE=EF,即GE为DF上的中线,
∴GE垂直平分DF.
17.解:操作与证明:
(1)BE=AD.
∵△C′DE绕点C按顺时针方向旋转30°,∴∠BCE=∠ACD=30度,
∵△ABC与△C′DE是等边三角形,∴CA=CB,CE=CD,
∴△BCE≌△ACD,∴BE=AD.
(2)BE=AD.
∵△C′DE绕点C按顺时针方向旋转的角度为α,∴∠BCE=∠ACD=α,
∵△ABC与△C′DE是等边三角形,∴CA=CB,CE=CD,
∴△BCE≌△ACD,∴BE=AD.
猜想与发现:
当α为180°时,线段AD的长度最大,等于a+b;当α为0°(或360°)时,线段AD的长度最小,等于a﹣b.
18.C.19.C.20.BC=EF 21.AC=AB
22、证明:∵∠1=∠2,∴∠1+ECA=∠2+∠ACE,即∠ACB=∠DCE,
在△ABC和△DEC中,∵∴△ABC≌△DEC(SAS).∴DE=AB.
23.证明:∵∠1=∠2,∴∠1+∠BAD=∠2+∠BAD,即:∠EAD=∠BAC,
在△EAD和△BAC中,∴△ABC≌△AED(ASA),∴BC=ED.
24、B 25、D. 26、D
27、(1)证明:∵△ADE是等腰直角三角形,F是AE中点,
∴DF⊥AE,DF=AF=EF,又∵∠ABC=90°,∠DCF,∠AMF都与∠MAC互余,
∴∠DCF=∠AMF,
在△DFC和△AFM中,,∴△DFC≌△AFM(AAS),
∴CF=MF,∴∠FMC=∠FCM;
(2)AD⊥MC,
理由:由(1)知,∠MFC=90°,FD=EF,FM=FC,∴∠FDE=∠FMC=45°,
∴DE∥CM,∴AD⊥MC.
28、(1)证明:∵在△ABC和△ADC中,∴△ABC≌△ADC(SSS),∴∠BAC=∠DAC,
∵在△ABF和△ADF中,∴△ABF≌△ADF,∴∠AFD=∠AFB,
∵∠AFB=∠CFE,∴∠AFD=∠CFE;
29、(1)证明:∵点D是AB中点,AC=BC,∠ACB=90°,
∴CD⊥AB,∠ACD=∠BCD=45°,∴∠CAD=∠CBD=45°,∴∠CAE=∠BCG,
又∵BF⊥CE,∴∠CBG+∠BCF=90°,
又∵∠ACE+∠BCF=90°,∴∠ACE=∠CBG,
在△AEC和△CGB中,
∴△AEC≌△CGB(ASA),∴AE=CG,
(2)解:BE=CM.
证明:∵CH⊥HM,CD⊥ED,
∴∠CMA+∠MCH=90°,∠BEC+∠MCH=90°,∴∠CMA=∠BEC,
又∵∠ACM=∠CBE=45°,
在△BCE和△CAM中,,∴△BCE≌△CAM(AAS),∴BE=CM.
( http: / / www.21cnjy.com )
一、知识梳理
1、 的两个三角形全等。即 。
2、 的两个三角形全等。即 。
3、 的两个三角形全等。即 。
4、 的两个三角形全等。即 。
5、 的两个三角形全等。即 。
6、全等三角形的 相等, 相等。证明两条线段(或两个角)相等,可以通过证明其所在的两个三角形 。
二、典例精析
1、(2013 舟山)如图,△ABC与△D ( http: / / www.21cnjy.com )CB中,AC与BD交于点E,且∠A=∠D,AB=DC.
(1)求证:△ABE≌DCE;
(2)当∠AEB=50°,求∠EBC的度数?
HYPERLINK "http://www.21cnjy.com"
2、(2013 珠海)如图,已知,EC=AC,∠BCE=∠DCA,∠A=∠E;求证:BC=DC.
HYPERLINK "http://www.21cnjy.com"
三、巩固提升
3.(2013 安顺)如图,已知AE=CF,∠AFD=∠CEB,那么添加下列一个条件后,仍无法判定△ADF≌△CBE的是( )
A. ∠A=∠C B. AD=CB C. BE=DF D. AD∥BC
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(3) (4) (5)
4.(2012 贵阳)如图,已知点A、D、 ( http: / / www.21cnjy.com )C、F在同一条直线上,AB=DE,BC=EF,要使△ABC≌△DEF,还需要添加一个条件是( )
A. ∠BCA=∠F B. ∠B=∠E C. BC∥EF D. ∠A=∠EDF
5.(2013 铁岭)如图,在△ABC和△DEC中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,不能添加的一组条件是( )
A. BC=EC,∠B=∠E B.BC=EC,AC=DC
C. BC=DC,∠A=∠D D.∠B=∠E,∠A=∠D
6.如图,某人把一块三角形的玻璃打碎成了三块,现在他要到玻璃店去配一块完全一样的玻璃,则他带的是第三块玻璃去,依据是( )
A.SSS B.SAS C. ASA D.AAS
7.(2013 湛江)如图,点B、F、C、E在一条直线上,FB=CE,AB∥ED,AC∥FD,求证:AC=DF.
( http: / / www.21cnjy.com )
8.(2013 玉林)如图,AB=AE,∠1=∠2,∠C=∠D.
求证:△ABC≌△AED.
( http: / / www.21cnjy.com )
9.(2013 武汉)如图,点E、F在BC上,BE=FC,AB=DC,∠B=∠C.求证:∠A=∠D.
( http: / / www.21cnjy.com )
10.(2013 泉州)如 ( http: / / www.21cnjy.com )图,已知AD是△ABC的中线,分别过点B、C作BE⊥AD于点E,CF⊥AD交AD的延长线于点F,求证:BE=CF.
( http: / / www.21cnjy.com )
四、拔高训练
11.(2009 芜湖)如图所示的4×4正方形网格中,
∠1+∠2+∠3+∠4+∠5+∠6+∠7=( )
A.330° B.315° C.310° D.320°
12.(2013 湖北)如图,已知△A ( http: / / www.21cnjy.com )BC≌△ADE,AB与ED交于点M,BC与ED,AD分别交于点F,N.请写出图中两对全等三角形(△ABC≌△ADE除外),并选择其中的一对加以证明.
( http: / / www.21cnjy.com )
13.(2013 大庆)如图,把一 ( http: / / www.21cnjy.com )个直角三角形ACB(∠ACB=90°)绕着顶点B顺时针旋转60°,使得点C旋转到AB边上的一点D,点A旋转到点E的位置.F,G分别是BD,BE上的点,BF=BG,延长CF与DG交于点H.
(1)求证:CF=DG;
(2)求出∠FHG的度数.
( http: / / www.21cnjy.com )
14.已知,如图,AB、CD相交于点O,AC∥DB,AO=BO,E、F分别是OC、OD中点.
求证:(1)OC=OD;
(2)求证:AE∥BF.
( http: / / www.21cnjy.com )
15.如图,点M、N分别在正三角形ABC的BC、CA边上,且BM=CN,AM、BN交于点Q,求∠AQN的度数.
( http: / / www.21cnjy.com )
16.(2012 镇江)如图,在四 ( http: / / www.21cnjy.com )边形ABCD中,AD∥BC,E是AB的中点,连接DE并延长交CB的延长线于点F,点G在边BC上,且∠GDF=∠ADF.
(1)求证:△ADE≌△BFE;
(2)连接EG,判断EG与DF的位置关系并说明理由.
( http: / / www.21cnjy.com )
17.(2008 房山区一模)阅读与理解:
图1是边长分别为a和b(a>b)的两个等边三角形纸片ABC和C′DE叠放在一起(C与C′重合)的图形.
操作与证明:
(1)操作:固定△ABC,将△C′DE绕点C ( http: / / www.21cnjy.com )按顺时针方向旋转30°,连接AD,BE,如图2;在图2中,线段BE与AD之间具有怎样的大小关系?证明你的结论;
( http: / / www.21cnjy.com )
(2)操作:若将图1中的△ ( http: / / www.21cnjy.com )C′DE,绕点C按顺时针方向任意旋转一个角度α,连接AD,BE,如图3;在图3中,线段BE与AD之间具有怎样的大小关系?证明你的结论;
猜想与发现:
根据上面的操作过程,请你猜想当α为多少度时,线段AD的长度最大是多少?当α为多少度时,线段AD的长度最小是多少?
五、课堂小测
18.(2013 来宾)如图,AB=AC,D,E分别是AB,AC上的点,下列条件中不能证明△ABE≌△ACD的是( )
A. AD=AE B. BD=CE C. BE=CD D. ∠B=∠C
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(18) (19) (20)
19.(2013 贺州)如图,在△ABC中,∠ABC=45°,AC=8cm,F是高AD和BE的交点,则BF的长是( )
20.(2013 昭通)如图,AF=DC,BC∥EF,只需补充一个条件 _________ ,就得△ABC≌△DEF.
21.(2013 义乌市 ( http: / / www.21cnjy.com ))如图,已知∠B=∠C,添加一个条件使△ABD≌△ACE(不标注新的字母,不添加新的线段),你添加的条件是 _________ .
22(2013 呼和浩特)如图,CD=CA,∠1=∠2,EC=BC,求证:DE=AB.
( http: / / www.21cnjy.com )
23(2012 重庆)已知:如图,AB=AE,∠1=∠2,∠B=∠E.求证:BC=ED.
( http: / / www.21cnjy.com )
六、体验中考
24、(2014年泰安)在△ABC和△A1B1C1中,下列四个命题:
(1)若AB=A1B1,AC=A1C1,∠A=∠A1,则△ABC≌△A1B1C1;
(2)若AB=A1B1,AC=A1C1,∠B=∠B1,则△ABC≌△A1B1C1;
(3)若∠A=∠A1,∠C=∠C1,则△ABC∽△A1B1C1;
(4)若AC:A1C1=CB:C1B1,∠C=∠C1,则△ABC∽△A1B1C1.
其中真命题的个数为( )
A.4个 B. 3个 C. 2个 D. 1个
25、(2014年泰安)将两个斜边长相 ( http: / / www.21cnjy.com )等的三角形纸片如图①放置,其中∠ACB=∠CED=90°,∠A=45°,∠D=30°.把△DCE绕点C顺时针旋转15°得到△D1CE1,如图②,连接D1B,则∠E1D1B的度数为( )
A.10° B. 20° C. 7.5° D. 15°
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(24) (25)
26、2012 泰安)如图,AB∥CD,E,F分别为AC,BD的中点,若AB=5,CD=3,则EF的长是( )
A. 4 B. 3 C. 2 D. 1
27、(2014年泰安)如图,∠ABC ( http: / / www.21cnjy.com )=90°,D、E分别在BC、AC上,AD⊥DE,且AD=DE,点F是AE的中点,FD与AB相交于点M.
(1)求证:∠FMC=∠FCM;
(2)AD与MC垂直吗?并说明理由.
( http: / / www.21cnjy.com )
28、(2013 泰安)如图,在四边形ABCD中,AB=AD,CB=CD,E是CD上一点,BE交AC于F,连接DF.
(1)证明:∠BAC=∠DAC,∠AFD=∠CFE.
( http: / / www.21cnjy.com )
29、(2011 泰安)已知:在△ABC中,AC=BC,∠ACB=90°,点D是AB的中点,点E是AB边上一点.
(1)直线BF垂直于直线CE于点F,交CD于点G(如图1),求证:AE=CG;
(2)直线AH垂直于直线CE,垂足为点H,交CD的延长线于点M(如图2),找出图中与BE相等的线段,并证明.
( http: / / www.21cnjy.com )
2014快乐暑假初二升初三衔接——三角形全等参考答案
1、证明:(1)∵在△ABE和△DCE中
∠A=∠D;∠AEB=∠DEC ;AB=DC
∴△ABE≌△DCE(AAS);
( http: / / www.21cnjy.com )解:(2)∵△ABE≌△DCE,∴BE=EC,
∴∠EBC=∠ECB,
∵∠EBC+∠ECB=∠AEB=50°,
∴∠EBC=25°.
2、证明:∵∠BCE=∠DCA,
∴∠BCE+∠ACE=∠DCA+∠ACE,即∠ACB=∠ECD,
在△ABC和△EDC中,
∠ACB=∠ECD,EC=AC;∠A=∠E
∴△ABC≌△EDC(ASA),∴BC=DC.
3.B.4.B.5.C.6.C.
7.证明:∵FB=CE,∴FB+FC=CE+FC,∴BC=EF,
∵AB∥ED,AC∥FD,∴∠B=∠E,∠ACB=∠DFE,
∵在△ABC和△DEF中,,∴△ABC≌△DEF(ASA),∴AC=DF.
8.证明:∵∠1=∠2,∴∠1+∠EAC=∠2+∠EAC,即∠BAC=∠EAD,
∵在△ABC和△AED中,,∴△ABC≌△AED(AAS).
9.证明:∵BE=FC,∴BE+EF=CF+EF,即BF=CE;
又∵AB=DC,∠B=∠C,∴△ABF≌△DCE;(SAS)∴∠A=∠D.
10.证明:∵AD是△ABC的中线,∴BD=CD,
∵BE⊥AD,CF⊥AD,∴∠BED=∠CFD=90°,
在△BDE和△CDF中,,∴△BDE≌△CDF(AAS),∴BE=CF.
11.B.
12.解:△AEM≌△ACN,△BMF≌△DNF,△ABN≌△ADM.
选择△AEM≌△ACN,理由如下:
∵△ADE≌△ABC,∴AE=AC,∠E=∠C,∠EAD=∠CAB,
∴∠EAM=∠CAN,
∵在△AEM和△ACN中,∴△AEM≌△ACN(ASA).
13.(1)证明:∵在△CBF和△DBG中,
,∴△CBF≌△DBG(SAS),∴CF=DG;
(2)解:∵△CBF≌△DBG,∴∠BCF=∠BDG,
又∵∠CFB=∠DFH,∴∠DHF=∠CBF=60°,
∴∠FHG=180°﹣∠DHF=180°﹣60°=120°.
14.证明:(1)∵AC∥BD,∴∠C=∠D,∠CAO=∠DBO,AO=BO,
∴△AOC≌△BOD,∴CO=DO;
(2)∵E、F分别是OC、OD的中点,∴OF=OD=OC=OE,
由AO=BO,EO=FO,
∴四边形AFBE是平行四边形,
∴AE∥BF.(其他方法:证明全等,在证明内错角相等也可)
15.解:∵BM=CN∴CM=AN,
又∵AB=AC,∠BAN=∠ACM,
∴△AMC≌△BNA,则∠BNA=∠AMC,
∵∠MAN+∠ANB+∠AQN=180°
∠MAN+∠AMC+∠ACB=180°,
∴∠AQN=∠ACB=60°.
16.(1)证明:∵AD∥BC,∴∠ADE=∠BFE,
∵E为AB的中点,∴AE=BE,
在△AED和△BFE中,,∴△AED≌△BFE(AAS);
(2)解:EG与DF的位置关系是EG垂直平分DF,理由为:连接EG,
∵∠GDF=∠ADE,∠ADE=∠BFE,
∴∠GDF=∠BFE,
由(1)△AED≌△BFE得:DE=EF,即GE为DF上的中线,
∴GE垂直平分DF.
17.解:操作与证明:
(1)BE=AD.
∵△C′DE绕点C按顺时针方向旋转30°,∴∠BCE=∠ACD=30度,
∵△ABC与△C′DE是等边三角形,∴CA=CB,CE=CD,
∴△BCE≌△ACD,∴BE=AD.
(2)BE=AD.
∵△C′DE绕点C按顺时针方向旋转的角度为α,∴∠BCE=∠ACD=α,
∵△ABC与△C′DE是等边三角形,∴CA=CB,CE=CD,
∴△BCE≌△ACD,∴BE=AD.
猜想与发现:
当α为180°时,线段AD的长度最大,等于a+b;当α为0°(或360°)时,线段AD的长度最小,等于a﹣b.
18.C.19.C.20.BC=EF 21.AC=AB
22、证明:∵∠1=∠2,∴∠1+ECA=∠2+∠ACE,即∠ACB=∠DCE,
在△ABC和△DEC中,∵∴△ABC≌△DEC(SAS).∴DE=AB.
23.证明:∵∠1=∠2,∴∠1+∠BAD=∠2+∠BAD,即:∠EAD=∠BAC,
在△EAD和△BAC中,∴△ABC≌△AED(ASA),∴BC=ED.
24、B 25、D. 26、D
27、(1)证明:∵△ADE是等腰直角三角形,F是AE中点,
∴DF⊥AE,DF=AF=EF,又∵∠ABC=90°,∠DCF,∠AMF都与∠MAC互余,
∴∠DCF=∠AMF,
在△DFC和△AFM中,,∴△DFC≌△AFM(AAS),
∴CF=MF,∴∠FMC=∠FCM;
(2)AD⊥MC,
理由:由(1)知,∠MFC=90°,FD=EF,FM=FC,∴∠FDE=∠FMC=45°,
∴DE∥CM,∴AD⊥MC.
28、(1)证明:∵在△ABC和△ADC中,∴△ABC≌△ADC(SSS),∴∠BAC=∠DAC,
∵在△ABF和△ADF中,∴△ABF≌△ADF,∴∠AFD=∠AFB,
∵∠AFB=∠CFE,∴∠AFD=∠CFE;
29、(1)证明:∵点D是AB中点,AC=BC,∠ACB=90°,
∴CD⊥AB,∠ACD=∠BCD=45°,∴∠CAD=∠CBD=45°,∴∠CAE=∠BCG,
又∵BF⊥CE,∴∠CBG+∠BCF=90°,
又∵∠ACE+∠BCF=90°,∴∠ACE=∠CBG,
在△AEC和△CGB中,
∴△AEC≌△CGB(ASA),∴AE=CG,
(2)解:BE=CM.
证明:∵CH⊥HM,CD⊥ED,
∴∠CMA+∠MCH=90°,∠BEC+∠MCH=90°,∴∠CMA=∠BEC,
又∵∠ACM=∠CBE=45°,
在△BCE和△CAM中,,∴△BCE≌△CAM(AAS),∴BE=CM.
( http: / / www.21cnjy.com )
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
