2014年快乐暑假初三升初四衔接复习部分——平行四边形(含答案)
文档属性
| 名称 | 2014年快乐暑假初三升初四衔接复习部分——平行四边形(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 117.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-07-13 18:08:24 | ||
图片预览

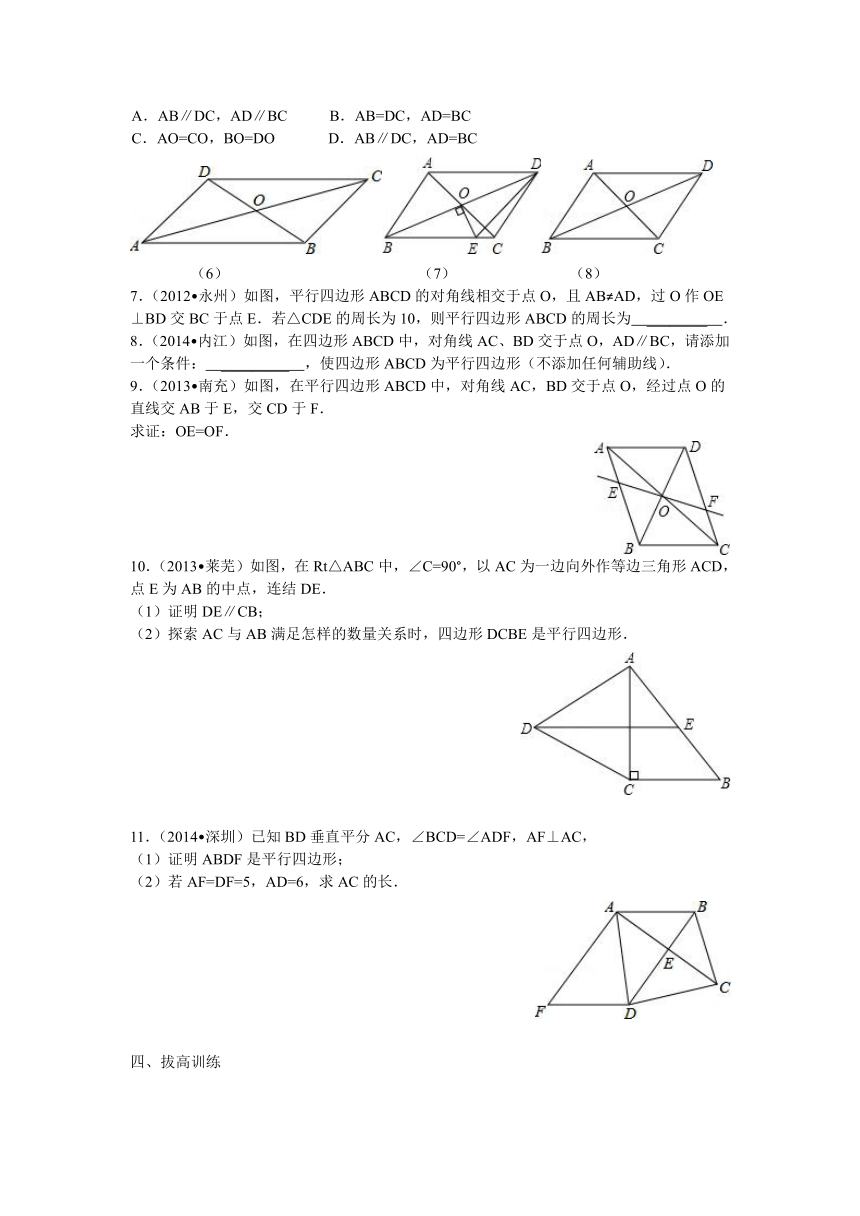
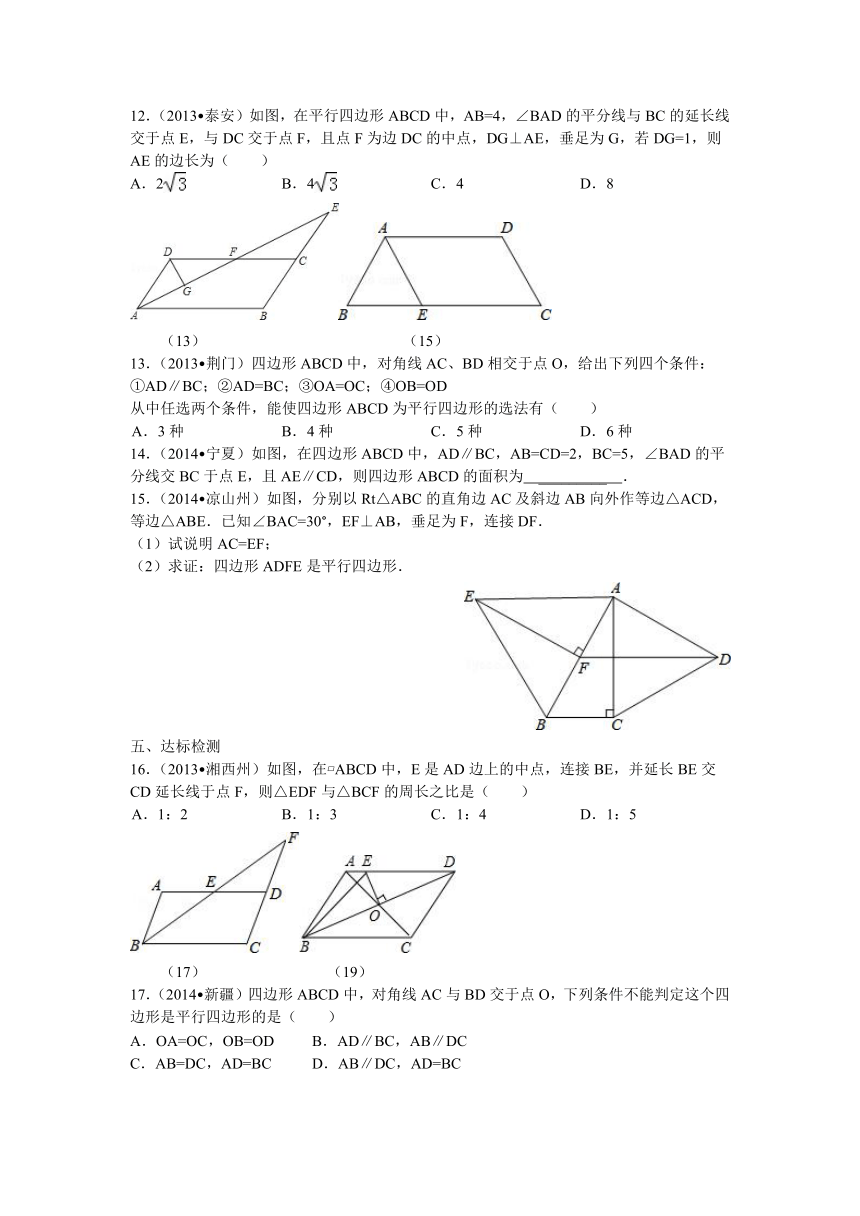
文档简介
2014年快乐暑假初三升初四衔接复习部分——平行四边形
一、知识梳理
1、平行四边形的性质:对边 ;对角 ;对角线 。
2、平行四边的评定方法:
从边的角度:两组对边 的四边形是平行四边形。
两组对边 的四边形是平行四边形。
一组对边 的四边形是平行四边形。
从对角线的角度: 的四边形是平行四边形。
从角的角度: 的四边形是平行四边形。
二、典例解析
1、(2014 上城区一模)如图,在 A ( http: / / www.21cnjy.com )BCD中,E为BC边上一点,且AB=AE.
(1)求证:△ABC≌EAD;
(2)若AE平分∠DAB,∠EAC=20°,求∠AED的度数.
HYPERLINK "http://www.21cnjy.com"
2、(2013 龙岩)如图,四边形ABCD是平行四边形,E、F是对角线AC上的两点,∠1=∠2.
(1)求证:AE=CF;
(2)求证:四边形EBFD是平行四边形.
( http: / / www.21cnjy.com )
三、巩固提升
3.(2013 益阳)如图,在平行四边形ABCD中,下列结论中错误的是( )
A. ∠1=∠2 B. ∠BAD=∠BCD C. AB=CD D. AC⊥BD
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(3) (4) (5)
4.(2013 云南)如图,平行四边形ABCD的对角线AC、BD相交于点O,下列结论正确的是( )
A.S ABCD=4S△AOB B.AC=BD C.AC⊥BD D. ABCD是轴对称图形
5.(2012 包头)如图,过 ABCD的 ( http: / / www.21cnjy.com )对角线BD上一点M分别作平行四边形两边的平行线EF与GH,那么图中的 AEMG的面积S1与 HCFM的面积S2的大小关系是( )
A. S1>S2 B. S1<S2 C. S1=S2 D. 2S1=S2
6.(2013 泸州)四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是( )
A. AB∥DC,AD∥BC B.AB=DC,AD=BC
C.AO=CO,BO=DO D.AB∥DC,AD=BC
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(6) (7) (8)
7.(2012 永州)如图,平行四边形AB ( http: / / www.21cnjy.com )CD的对角线相交于点O,且AB≠AD,过O作OE⊥BD交BC于点E.若△CDE的周长为10,则平行四边形ABCD的周长为 ________ .
8.(2014 内江)如图 ( http: / / www.21cnjy.com ),在四边形ABCD中,对角线AC、BD交于点O,AD∥BC,请添加一个条件: _________ ,使四边形ABCD为平行四边形(不添加任何辅助线).
9.(2013 南充)如图,在平行四边形ABCD中,对角线AC,BD交于点O,经过点O的直线交AB于E,交CD于F.
求证:OE=OF.
( http: / / www.21cnjy.com )
10.(2013 莱芜)如图,在Rt△ABC中,∠C=90°,以AC为一边向外作等边三角形ACD,点E为AB的中点,连结DE.
(1)证明DE∥CB;
(2)探索AC与AB满足怎样的数量关系时,四边形DCBE是平行四边形.
( http: / / www.21cnjy.com )
11.(2014 深圳)已知BD垂直平分AC,∠BCD=∠ADF,AF⊥AC,
(1)证明ABDF是平行四边形;
(2)若AF=DF=5,AD=6,求AC的长.
( http: / / www.21cnjy.com )
四、拔高训练
12.(2013 泰安)如图,在平行四 ( http: / / www.21cnjy.com )边形ABCD中,AB=4,∠BAD的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点,DG⊥AE,垂足为G,若DG=1,则AE的边长为( )
A.2 B. 4 C. 4 D. 8
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(13) (15)
13.(2013 荆门)四边形ABCD中,对角线AC、BD相交于点O,给出下列四个条件:
①AD∥BC;②AD=BC;③OA=OC;④OB=OD
从中任选两个条件,能使四边形ABCD为平行四边形的选法有( )
A. 3种 B. 4种 C. 5种 D. 6种
14.(2014 宁夏)如图,在四 ( http: / / www.21cnjy.com )边形ABCD中,AD∥BC,AB=CD=2,BC=5,∠BAD的平分线交BC于点E,且AE∥CD,则四边形ABCD的面积为 _________ .
15.(2014 凉山州)如图,分 ( http: / / www.21cnjy.com )别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD,等边△ABE.已知∠BAC=30°,EF⊥AB,垂足为F,连接DF.
(1)试说明AC=EF;
(2)求证:四边形ADFE是平行四边形.
( http: / / www.21cnjy.com )
五、达标检测
16.(2013 湘西州)如图,在 ABCD ( http: / / www.21cnjy.com )中,E是AD边上的中点,连接BE,并延长BE交CD延长线于点F,则△EDF与△BCF的周长之比是( )
A.1:2 B. 1:3 C. 1:4 D. 1:5
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(17) (19)
17.(2014 新疆)四边形ABCD中,对角线AC与BD交于点O,下列条件不能判定这个四边形是平行四边形的是( )
A.OA=OC,OB=OD B.AD∥BC,AB∥DC
C.AB=DC,AD=BC D.AB∥DC,AD=BC
18.(2012 乌鲁木齐 ( http: / / www.21cnjy.com ))如图,在周长为20的平行四边形ABCD中,AB<AD,AC与BD交于点O,OE⊥BD,交AD于点E,则△ABE的周长为 _________ .
19.(2007 南平) ( http: / / www.21cnjy.com )请从①AB∥CD;②BC=AD;③BC∥AD;④AB=CD这四个条件中选取两个,使四边形ABCD成为平行四边形: _________ .(只需填写所选取的两个条件的序号即可)
20.(2012 乌鲁木齐)如图,E、F是平行四边形ABCD对角线AC上的两点,且BE∥DF,
求证:BF=DE.
( http: / / www.21cnjy.com )
21.(2013 梧州)如图,已知:AB∥CD,BE⊥AD,垂足为点E,CF⊥AD,垂足为点F,并且AE=DF.
求证:四边形BECF是平行四边形.
( http: / / www.21cnjy.com )
2014年初三升初四衔接复习部分——平行四边形参考答案
1、解:(1)∵在平行四边形ABCD中 ( http: / / www.21cnjy.com ),AD∥BC,BC=AD,
∴∠EAD=∠AEB,
又∵AB=AE,∴∠B=∠AEB,∴∠B=∠EAD,
在△ABC和△EAD中,
AB=AE,∠ABC=∠EAD,BC=AD
∴△ABC≌△EAD.
(2)∵AE平分∠DAB,∴∠BAE=∠DAE,∴∠BAE=∠AEB=∠B,
∴△ABE为等边三角形,∴∠BAE=6 ( http: / / www.21cnjy.com )0°,
∴∠BAC=∠BAE+∠EAC=80°,
∵△ABC≌△EAD,
∴∠AED=∠BAC=80°.
2、(1)证明:如图:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,∠3=∠4,
∵∠1=∠3+∠5,∠2=∠4+∠6,∠1=∠2 ∴∠5=∠6
∵在△ADE与△CBF中,∴△ADE≌△CBF(ASA),∴AE=CF;
(2)证明:∵∠1=∠2,∴DE∥BF.
又∵由(1)知△ADE≌△CBF,
∴DE=BF,
∴四边形EBFD是平行四边形.
3.D.4.A.5.C.6.D.7. 20 8.AD=BC(答案不唯一)
9.证明:∵四边形ABCD是平行四边形,
∴OA=OC,AB∥CD,∴∠OAE=∠OCF,
∵在△OAE和△OCF中,,∴△OAE≌△OCF(ASA),∴OE=OF.
10.(1)证明:连结CE.
∵点E为Rt△ACB的斜边AB的中点,∴CE=AB=AE.
∵△ACD是等边三角形,∴AD=CD.
在△ADE与△CDE中,,
∴△ADE≌△CDE(SSS),
∴∠ADE=∠CDE=30°.
∵∠DCB=150°,∴∠EDC+∠DCB=180°.
∴DE∥CB.
(2)解:∵∠DCB=150°,
若四边形DCBE是平行四边形,则DC∥BE,∠DCB+∠B=180°.
∴∠B=30°.
在Rt△ACB中,sinB=,sin30°==,AC=或AB=2AC.
∴当AC=或AB=2AC时,四边形DCBE是平行四边形.
11.(1)证明:∵BD垂直平分AC,∴AB=BC,AD=DC,
在△ADB与△CDB中,,∴△ADB≌△CDB(SSS)∴∠BCD=∠BAD,
∵∠BCD=∠ADF,∴∠BAD=∠ADF,∴AB∥FD,
∵BD⊥AC,AF⊥AC, ∴AF∥BD,
∴四边形ABDF是平行四边形,
(2)解:∵四边形ABDF是平行四边形,AF=DF=5,∴ ABDF是菱形,∴AB=BD=5,
∵AD=6,
设BE=x,则DE=5﹣x,
∴AB2﹣BE2=AD2﹣DE2,即52﹣x2=62﹣(5﹣x)2
解得:x=,∴=, ∴AC=2AE=.
12.B.13.B.14.
15.证明:(1)∵Rt△ABC中,∠BAC=30°,∴AB=2BC,
又∵△ABE是等边三角形,EF⊥AB,∴AB=2AF∴AF=BC,
在Rt△AFE和Rt△BCA中,,∴△AFE≌△BCA(HL),∴AC=EF;
(2)∵△ACD是等边三角形,∴∠DAC=60°,AC=AD,∴∠DAB=∠DAC+∠BAC=90°
∴EF∥AD,
∵AC=EF,AC=AD,∴EF=AD,∴四边形ADFE是平行四边形.
16.A.17.D.18.10 19. 1与3,或2与4,或1与4,或2与3
20.证明:∵四边形ABCD是平行四边形,∴AD=CB,AD∥CB,∴∠BCE=∠DAF
又∵BE∥DF,∴∠BEC=∠DFA
在△CEB和△AFD中,
∠BCE=∠DAF,∠BEC=∠DFA,BC=DA
∴△CEB≌△AFD(AAS)
∴BE=DF
故BFED为平行四边形.
∴BF=DE.
21.证明:∵BE⊥AD,CF⊥AD,∴∠AEB=∠DFC=90°,
∵AB∥CD,∴∠A=∠D,
在△AEB与△DFC中,,∴△AEB≌△DFC(ASA),∴BE=CF.
∵BE⊥AD,CF⊥AD,
∴BE∥CF.
∴四边形BECF是平行四边形.
一、知识梳理
1、平行四边形的性质:对边 ;对角 ;对角线 。
2、平行四边的评定方法:
从边的角度:两组对边 的四边形是平行四边形。
两组对边 的四边形是平行四边形。
一组对边 的四边形是平行四边形。
从对角线的角度: 的四边形是平行四边形。
从角的角度: 的四边形是平行四边形。
二、典例解析
1、(2014 上城区一模)如图,在 A ( http: / / www.21cnjy.com )BCD中,E为BC边上一点,且AB=AE.
(1)求证:△ABC≌EAD;
(2)若AE平分∠DAB,∠EAC=20°,求∠AED的度数.
HYPERLINK "http://www.21cnjy.com"
2、(2013 龙岩)如图,四边形ABCD是平行四边形,E、F是对角线AC上的两点,∠1=∠2.
(1)求证:AE=CF;
(2)求证:四边形EBFD是平行四边形.
( http: / / www.21cnjy.com )
三、巩固提升
3.(2013 益阳)如图,在平行四边形ABCD中,下列结论中错误的是( )
A. ∠1=∠2 B. ∠BAD=∠BCD C. AB=CD D. AC⊥BD
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(3) (4) (5)
4.(2013 云南)如图,平行四边形ABCD的对角线AC、BD相交于点O,下列结论正确的是( )
A.S ABCD=4S△AOB B.AC=BD C.AC⊥BD D. ABCD是轴对称图形
5.(2012 包头)如图,过 ABCD的 ( http: / / www.21cnjy.com )对角线BD上一点M分别作平行四边形两边的平行线EF与GH,那么图中的 AEMG的面积S1与 HCFM的面积S2的大小关系是( )
A. S1>S2 B. S1<S2 C. S1=S2 D. 2S1=S2
6.(2013 泸州)四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是( )
A. AB∥DC,AD∥BC B.AB=DC,AD=BC
C.AO=CO,BO=DO D.AB∥DC,AD=BC
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(6) (7) (8)
7.(2012 永州)如图,平行四边形AB ( http: / / www.21cnjy.com )CD的对角线相交于点O,且AB≠AD,过O作OE⊥BD交BC于点E.若△CDE的周长为10,则平行四边形ABCD的周长为 ________ .
8.(2014 内江)如图 ( http: / / www.21cnjy.com ),在四边形ABCD中,对角线AC、BD交于点O,AD∥BC,请添加一个条件: _________ ,使四边形ABCD为平行四边形(不添加任何辅助线).
9.(2013 南充)如图,在平行四边形ABCD中,对角线AC,BD交于点O,经过点O的直线交AB于E,交CD于F.
求证:OE=OF.
( http: / / www.21cnjy.com )
10.(2013 莱芜)如图,在Rt△ABC中,∠C=90°,以AC为一边向外作等边三角形ACD,点E为AB的中点,连结DE.
(1)证明DE∥CB;
(2)探索AC与AB满足怎样的数量关系时,四边形DCBE是平行四边形.
( http: / / www.21cnjy.com )
11.(2014 深圳)已知BD垂直平分AC,∠BCD=∠ADF,AF⊥AC,
(1)证明ABDF是平行四边形;
(2)若AF=DF=5,AD=6,求AC的长.
( http: / / www.21cnjy.com )
四、拔高训练
12.(2013 泰安)如图,在平行四 ( http: / / www.21cnjy.com )边形ABCD中,AB=4,∠BAD的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点,DG⊥AE,垂足为G,若DG=1,则AE的边长为( )
A.2 B. 4 C. 4 D. 8
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(13) (15)
13.(2013 荆门)四边形ABCD中,对角线AC、BD相交于点O,给出下列四个条件:
①AD∥BC;②AD=BC;③OA=OC;④OB=OD
从中任选两个条件,能使四边形ABCD为平行四边形的选法有( )
A. 3种 B. 4种 C. 5种 D. 6种
14.(2014 宁夏)如图,在四 ( http: / / www.21cnjy.com )边形ABCD中,AD∥BC,AB=CD=2,BC=5,∠BAD的平分线交BC于点E,且AE∥CD,则四边形ABCD的面积为 _________ .
15.(2014 凉山州)如图,分 ( http: / / www.21cnjy.com )别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD,等边△ABE.已知∠BAC=30°,EF⊥AB,垂足为F,连接DF.
(1)试说明AC=EF;
(2)求证:四边形ADFE是平行四边形.
( http: / / www.21cnjy.com )
五、达标检测
16.(2013 湘西州)如图,在 ABCD ( http: / / www.21cnjy.com )中,E是AD边上的中点,连接BE,并延长BE交CD延长线于点F,则△EDF与△BCF的周长之比是( )
A.1:2 B. 1:3 C. 1:4 D. 1:5
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(17) (19)
17.(2014 新疆)四边形ABCD中,对角线AC与BD交于点O,下列条件不能判定这个四边形是平行四边形的是( )
A.OA=OC,OB=OD B.AD∥BC,AB∥DC
C.AB=DC,AD=BC D.AB∥DC,AD=BC
18.(2012 乌鲁木齐 ( http: / / www.21cnjy.com ))如图,在周长为20的平行四边形ABCD中,AB<AD,AC与BD交于点O,OE⊥BD,交AD于点E,则△ABE的周长为 _________ .
19.(2007 南平) ( http: / / www.21cnjy.com )请从①AB∥CD;②BC=AD;③BC∥AD;④AB=CD这四个条件中选取两个,使四边形ABCD成为平行四边形: _________ .(只需填写所选取的两个条件的序号即可)
20.(2012 乌鲁木齐)如图,E、F是平行四边形ABCD对角线AC上的两点,且BE∥DF,
求证:BF=DE.
( http: / / www.21cnjy.com )
21.(2013 梧州)如图,已知:AB∥CD,BE⊥AD,垂足为点E,CF⊥AD,垂足为点F,并且AE=DF.
求证:四边形BECF是平行四边形.
( http: / / www.21cnjy.com )
2014年初三升初四衔接复习部分——平行四边形参考答案
1、解:(1)∵在平行四边形ABCD中 ( http: / / www.21cnjy.com ),AD∥BC,BC=AD,
∴∠EAD=∠AEB,
又∵AB=AE,∴∠B=∠AEB,∴∠B=∠EAD,
在△ABC和△EAD中,
AB=AE,∠ABC=∠EAD,BC=AD
∴△ABC≌△EAD.
(2)∵AE平分∠DAB,∴∠BAE=∠DAE,∴∠BAE=∠AEB=∠B,
∴△ABE为等边三角形,∴∠BAE=6 ( http: / / www.21cnjy.com )0°,
∴∠BAC=∠BAE+∠EAC=80°,
∵△ABC≌△EAD,
∴∠AED=∠BAC=80°.
2、(1)证明:如图:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,∠3=∠4,
∵∠1=∠3+∠5,∠2=∠4+∠6,∠1=∠2 ∴∠5=∠6
∵在△ADE与△CBF中,∴△ADE≌△CBF(ASA),∴AE=CF;
(2)证明:∵∠1=∠2,∴DE∥BF.
又∵由(1)知△ADE≌△CBF,
∴DE=BF,
∴四边形EBFD是平行四边形.
3.D.4.A.5.C.6.D.7. 20 8.AD=BC(答案不唯一)
9.证明:∵四边形ABCD是平行四边形,
∴OA=OC,AB∥CD,∴∠OAE=∠OCF,
∵在△OAE和△OCF中,,∴△OAE≌△OCF(ASA),∴OE=OF.
10.(1)证明:连结CE.
∵点E为Rt△ACB的斜边AB的中点,∴CE=AB=AE.
∵△ACD是等边三角形,∴AD=CD.
在△ADE与△CDE中,,
∴△ADE≌△CDE(SSS),
∴∠ADE=∠CDE=30°.
∵∠DCB=150°,∴∠EDC+∠DCB=180°.
∴DE∥CB.
(2)解:∵∠DCB=150°,
若四边形DCBE是平行四边形,则DC∥BE,∠DCB+∠B=180°.
∴∠B=30°.
在Rt△ACB中,sinB=,sin30°==,AC=或AB=2AC.
∴当AC=或AB=2AC时,四边形DCBE是平行四边形.
11.(1)证明:∵BD垂直平分AC,∴AB=BC,AD=DC,
在△ADB与△CDB中,,∴△ADB≌△CDB(SSS)∴∠BCD=∠BAD,
∵∠BCD=∠ADF,∴∠BAD=∠ADF,∴AB∥FD,
∵BD⊥AC,AF⊥AC, ∴AF∥BD,
∴四边形ABDF是平行四边形,
(2)解:∵四边形ABDF是平行四边形,AF=DF=5,∴ ABDF是菱形,∴AB=BD=5,
∵AD=6,
设BE=x,则DE=5﹣x,
∴AB2﹣BE2=AD2﹣DE2,即52﹣x2=62﹣(5﹣x)2
解得:x=,∴=, ∴AC=2AE=.
12.B.13.B.14.
15.证明:(1)∵Rt△ABC中,∠BAC=30°,∴AB=2BC,
又∵△ABE是等边三角形,EF⊥AB,∴AB=2AF∴AF=BC,
在Rt△AFE和Rt△BCA中,,∴△AFE≌△BCA(HL),∴AC=EF;
(2)∵△ACD是等边三角形,∴∠DAC=60°,AC=AD,∴∠DAB=∠DAC+∠BAC=90°
∴EF∥AD,
∵AC=EF,AC=AD,∴EF=AD,∴四边形ADFE是平行四边形.
16.A.17.D.18.10 19. 1与3,或2与4,或1与4,或2与3
20.证明:∵四边形ABCD是平行四边形,∴AD=CB,AD∥CB,∴∠BCE=∠DAF
又∵BE∥DF,∴∠BEC=∠DFA
在△CEB和△AFD中,
∠BCE=∠DAF,∠BEC=∠DFA,BC=DA
∴△CEB≌△AFD(AAS)
∴BE=DF
故BFED为平行四边形.
∴BF=DE.
21.证明:∵BE⊥AD,CF⊥AD,∴∠AEB=∠DFC=90°,
∵AB∥CD,∴∠A=∠D,
在△AEB与△DFC中,,∴△AEB≌△DFC(ASA),∴BE=CF.
∵BE⊥AD,CF⊥AD,
∴BE∥CF.
∴四边形BECF是平行四边形.
