归纳推理[下学期]
图片预览



文档简介
课件11张PPT。
合情推理
--归纳推理【引例1】
观察下列算式:
1 + 3 = 4 = 22
1 + 3 + 5 = 9 = 32
1 + 3 + 5 + 7 = 16 = 42
1 + 3 + 5 + 7 + 9 = 25 = 52
??
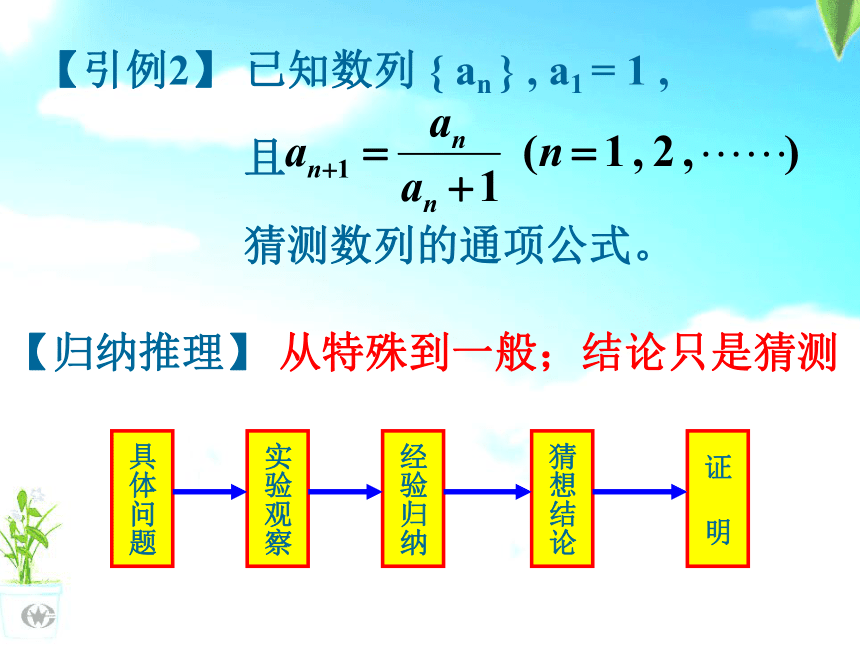
你能得出怎样的结论?【引例2】 已知数列 { an } , a1 = 1 ,
且
猜测数列的通项公式。 【归纳推理】 从特殊到一般;结论只是猜测【思考下列问题】1、设 an 表示 n 条直线交点的最多个数,
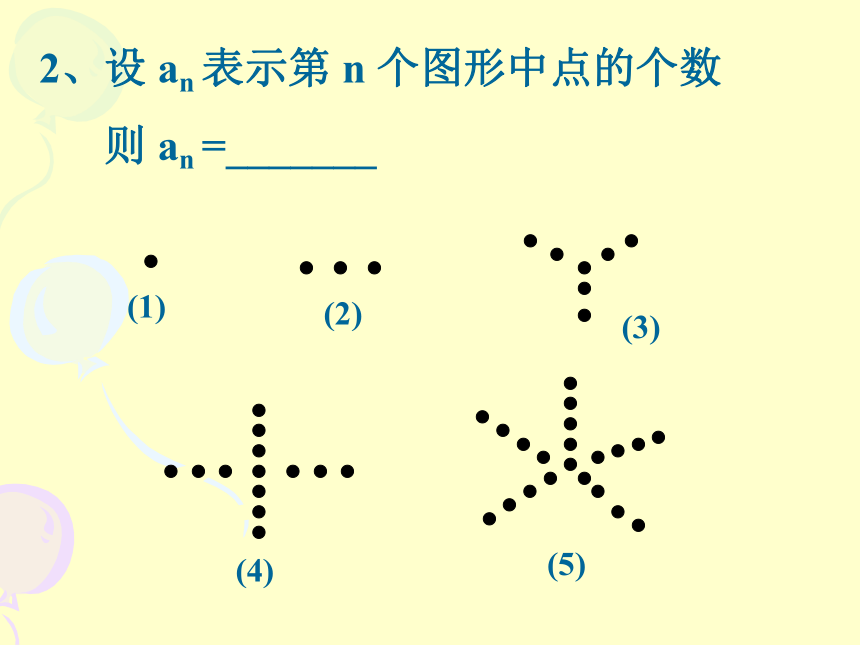
则 an =________ 2 条直线相交最多有1个交点 3 条直线相交最多有3个交点 4 条直线相交最多有6个交点2、设 an 表示第 n 个图形中点的个数
则 an =_______(1)(2)(3)(4)(5)3、下面是一系列有机物的结构简图,图中的小黑点表示原子,两黑点间的短线表示化学键,则第n个图有_____原子,有______个化学键(1)(2)(3) 4、 用半径相同的小球,堆在一起,成
一个 “正三棱锥” 型,第一层 1 个 ,
第二层 3 个,则第三层有______个,
第 n 层有_______个。(设 n > 1 ,小
球不滚动)
【例1】 比较 2005 2006 与 2006 2005 的大小。【分析】 n = 1 , 12 < 21
n = 2 , 23 < 32
n = 3 , 34 > 43
n = 4 , 45 > 54
n = 5 , 56 > 65
【猜测】 n n+1 > (n+1) n
( n ≥ 3 )【例2】 根据关系式,猜测 Sn = ?【分析】【结论】你能证明吗?【练习】
1、观察由上述事实你能得出怎样的结论?2、设 【作业】 P44 A组 1、2、3、4、53、有n枚正面向上的硬币,每次任意翻转
n – 1 枚,问能否把 n枚硬币全部翻转为
反面向上?
合情推理
--归纳推理【引例1】
观察下列算式:
1 + 3 = 4 = 22
1 + 3 + 5 = 9 = 32
1 + 3 + 5 + 7 = 16 = 42
1 + 3 + 5 + 7 + 9 = 25 = 52
??
你能得出怎样的结论?【引例2】 已知数列 { an } , a1 = 1 ,
且
猜测数列的通项公式。 【归纳推理】 从特殊到一般;结论只是猜测【思考下列问题】1、设 an 表示 n 条直线交点的最多个数,
则 an =________ 2 条直线相交最多有1个交点 3 条直线相交最多有3个交点 4 条直线相交最多有6个交点2、设 an 表示第 n 个图形中点的个数
则 an =_______(1)(2)(3)(4)(5)3、下面是一系列有机物的结构简图,图中的小黑点表示原子,两黑点间的短线表示化学键,则第n个图有_____原子,有______个化学键(1)(2)(3) 4、 用半径相同的小球,堆在一起,成
一个 “正三棱锥” 型,第一层 1 个 ,
第二层 3 个,则第三层有______个,
第 n 层有_______个。(设 n > 1 ,小
球不滚动)
【例1】 比较 2005 2006 与 2006 2005 的大小。【分析】 n = 1 , 12 < 21
n = 2 , 23 < 32
n = 3 , 34 > 43
n = 4 , 45 > 54
n = 5 , 56 > 65
【猜测】 n n+1 > (n+1) n
( n ≥ 3 )【例2】 根据关系式,猜测 Sn = ?【分析】【结论】你能证明吗?【练习】
1、观察由上述事实你能得出怎样的结论?2、设 【作业】 P44 A组 1、2、3、4、53、有n枚正面向上的硬币,每次任意翻转
n – 1 枚,问能否把 n枚硬币全部翻转为
反面向上?
