7.3.2 离散型随机变量的方差 教学设计(表格式)
文档属性
| 名称 | 7.3.2 离散型随机变量的方差 教学设计(表格式) |

|
|
| 格式 | docx | ||
| 文件大小 | 84.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-10 07:26:44 | ||
图片预览

文档简介
教学设计
课程基本信息
学 科 高中数学 年 级 高二 学 期 春季
课 题 7.3.2离散型随机变量的方差(第一课时)
教科书 书 名:普通高中数学教材 出版社:人民教育出版社 出版日期:2023年3月
教学内容分析
本节课选自《2019人教A版高中数学选择性必修第三册》第67-70页的第七章7.3.2离散型随机变量的方差。 本单元内容主要包括随机变量的均值和方差。本节课是前面学习完随机变量分布列的基础上进行研究的,知识上具有承前启后的作用。随机变量的均值和方差是概率论和数理统计的重要概念,节课是从实际出发,通过抽象思维,建立数学模型,进而认知数学理论,应用于实际的过程。
教学目标分析
通过实例,让学生了解随机变量的均值只能反映取值的集中程度,不能反映随机变量取值的离散程度,体会引入离散型随机变量的方差的必要性。理解离散型随机变量方差的概念,了解其实际含义。并会计算简单的离散型随机变量的均值和方差,并利用均值与方差在实际问题中得出科学的决策。通过两个例子计算离散型随机变量的方差,体会引入离散型随机变量的均值和方差的必要性。体会它在实际生产生活中的应用价值。
学生学情分析(含教学重难点分析)
重点:理解离散型随机变量的方差、标准差的概念及其求解。 难点:比较两个随机变量的均值与方差的大小,利用离散型随机变量的方差、标准差解决一些实际问题。
教学方法和策略分析
教学方法:讲授法、讨论法、自学展示 教学策略:启发式教学策略
教学手段
现代多媒体教学
教学过程
环节一:探索方差如何定量离散型随机变量取值的离散程度 随机变量的均值是一个重要的数字特征,它反映了随机变量取值的平均水平或分布的“集中趋势”.因为随机变量的取值围绕其均值波动,而随机变量的均值无法反映波动幅度的大小.所以我们还需要寻找反映随机变量取值波动大小的数字特征. 问题 1:从两名同学中挑出一名代表班级参加射击比赛。根据以往的成绩记录,甲、乙两名同学击中目标靶的环数X和Y的分布列如下表1和表2所示:如何评价这两名同学的射击水平? 表1 X678910 P0.090.240.320.280.07
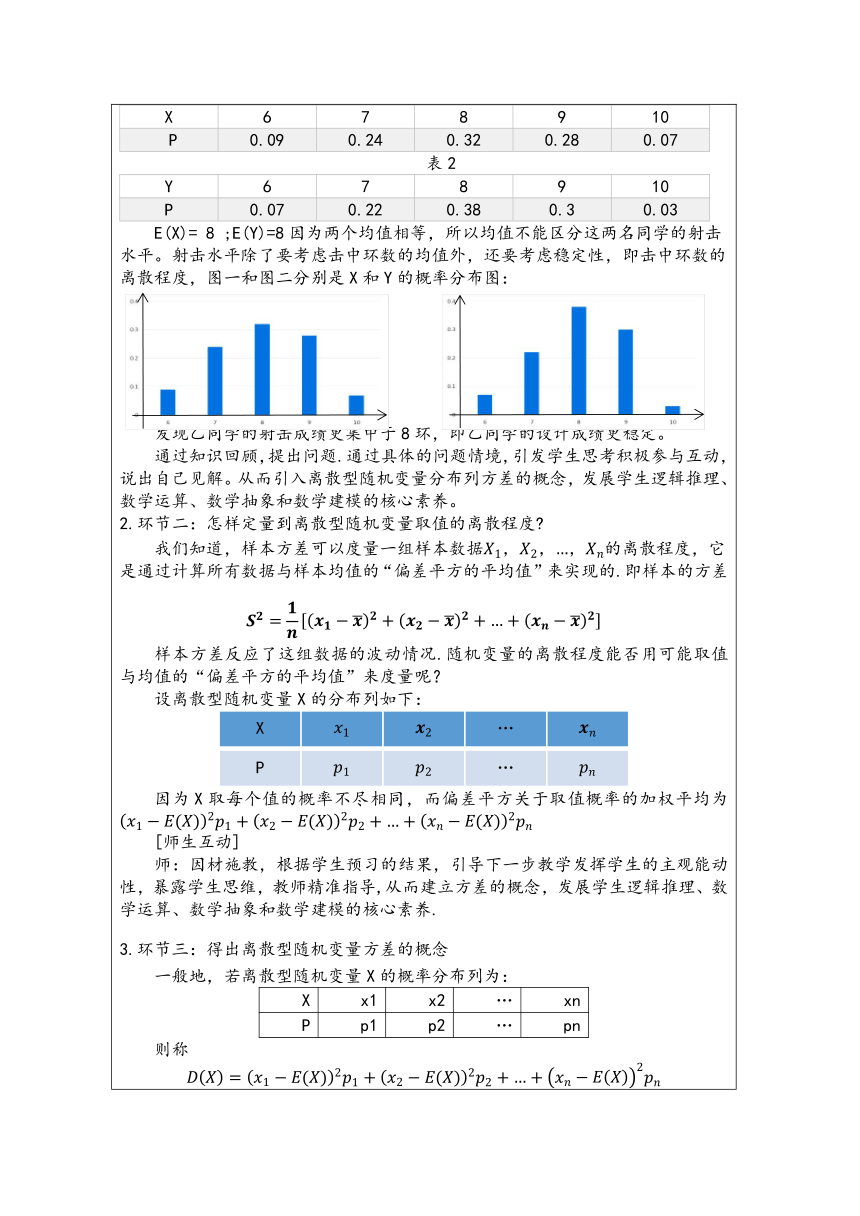
表2 Y678910P0.070.220.380.30.03
E(X)= 8 ;E(Y)=8因为两个均值相等,所以均值不能区分这两名同学的射击水平。射击水平除了要考虑击中环数的均值外,还要考虑稳定性,即击中环数的离散程度,图一和图二分别是X和Y的概率分布图: 图一 图二 发现乙同学的射击成绩更集中于8环,即乙同学的设计成绩更稳定。 通过知识回顾,提出问题.通过具体的问题情境,引发学生思考积极参与互动,说出自己见解。从而引入离散型随机变量分布列方差的概念,发展学生逻辑推理、数学运算、数学抽象和数学建模的核心素养。 2.环节二:怎样定量到离散型随机变量取值的离散程度 我们知道,样本方差可以度量一组样本数据的离散程度,它是通过计算所有数据与样本均值的“偏差平方的平均值”来实现的.即样本的方差 样本方差反应了这组数据的波动情况.随机变量的离散程度能否用可能取值与均值的“偏差平方的平均值”来度量呢? 设离散型随机变量X的分布列如下: X…P…
因为X取每个值的概率不尽相同,而偏差平方关于取值概率的加权平均为 [师生互动] 师:因材施教,根据学生预习的结果,引导下一步教学发挥学生的主观能动性,暴露学生思维,教师精准指导,从而建立方差的概念,发展学生逻辑推理、数学运算、数学抽象和数学建模的核心素养. 3.环节三:得出离散型随机变量方差的概念 一般地,若离散型随机变量X的概率分布列为: Xx1x2…xnPp1p2…pn
则称 为随机变量X的方差,称为随机变量X的标准差。 师:随机变量的方差与标准差都反映了随机变量取值的稳定与波动,集中与分散的程度.那是方差越大越稳定吗? 生:加深学方差或标准差越小,随机变量的取值越集中;方差或标准差越大,随机变量的取值越分散. 4.环节四:课堂练习 例1: 已知随机变量X的分布列如下 X0124P0.10.20.40.1
求D(X) 解: 例2 投资A、B两种股票,每股收益的分布列分别如表1和表2所示: 表1 股票A收益的分布列 表2 股票B收益的分布列 (1)投资哪种股票的期望收益大? 解:股票A和股票B投资收益的期望分别为 因为,所以投资股票A的期望收益较大 (2)投资哪种股票的风险高? 解:股票A和股票B投资收益的方差分别为 D D 因为相差不大,且D,所以投资股票A的风险更大. 【设计意图】通过典例剖析,让学生体会方差的一般方法,加深学生对方差的理解和运用,感受数学模型在数学应用中的价值。发展学生逻辑推理,直观想象、数学抽象和数学运算的核心素养。 5.环节五:课堂小结 1、离散型随机变量的方差 2、利用均值和方差的意义解决实际问题的步骤 (1)比较均值. (2)在均值相等或接近的情况下计算方差 (3)得出结论.方差越小结果越稳定 6.环节六:作业布置 7.环节七:教学反思
课程基本信息
学 科 高中数学 年 级 高二 学 期 春季
课 题 7.3.2离散型随机变量的方差(第一课时)
教科书 书 名:普通高中数学教材 出版社:人民教育出版社 出版日期:2023年3月
教学内容分析
本节课选自《2019人教A版高中数学选择性必修第三册》第67-70页的第七章7.3.2离散型随机变量的方差。 本单元内容主要包括随机变量的均值和方差。本节课是前面学习完随机变量分布列的基础上进行研究的,知识上具有承前启后的作用。随机变量的均值和方差是概率论和数理统计的重要概念,节课是从实际出发,通过抽象思维,建立数学模型,进而认知数学理论,应用于实际的过程。
教学目标分析
通过实例,让学生了解随机变量的均值只能反映取值的集中程度,不能反映随机变量取值的离散程度,体会引入离散型随机变量的方差的必要性。理解离散型随机变量方差的概念,了解其实际含义。并会计算简单的离散型随机变量的均值和方差,并利用均值与方差在实际问题中得出科学的决策。通过两个例子计算离散型随机变量的方差,体会引入离散型随机变量的均值和方差的必要性。体会它在实际生产生活中的应用价值。
学生学情分析(含教学重难点分析)
重点:理解离散型随机变量的方差、标准差的概念及其求解。 难点:比较两个随机变量的均值与方差的大小,利用离散型随机变量的方差、标准差解决一些实际问题。
教学方法和策略分析
教学方法:讲授法、讨论法、自学展示 教学策略:启发式教学策略
教学手段
现代多媒体教学
教学过程
环节一:探索方差如何定量离散型随机变量取值的离散程度 随机变量的均值是一个重要的数字特征,它反映了随机变量取值的平均水平或分布的“集中趋势”.因为随机变量的取值围绕其均值波动,而随机变量的均值无法反映波动幅度的大小.所以我们还需要寻找反映随机变量取值波动大小的数字特征. 问题 1:从两名同学中挑出一名代表班级参加射击比赛。根据以往的成绩记录,甲、乙两名同学击中目标靶的环数X和Y的分布列如下表1和表2所示:如何评价这两名同学的射击水平? 表1 X678910 P0.090.240.320.280.07
表2 Y678910P0.070.220.380.30.03
E(X)= 8 ;E(Y)=8因为两个均值相等,所以均值不能区分这两名同学的射击水平。射击水平除了要考虑击中环数的均值外,还要考虑稳定性,即击中环数的离散程度,图一和图二分别是X和Y的概率分布图: 图一 图二 发现乙同学的射击成绩更集中于8环,即乙同学的设计成绩更稳定。 通过知识回顾,提出问题.通过具体的问题情境,引发学生思考积极参与互动,说出自己见解。从而引入离散型随机变量分布列方差的概念,发展学生逻辑推理、数学运算、数学抽象和数学建模的核心素养。 2.环节二:怎样定量到离散型随机变量取值的离散程度 我们知道,样本方差可以度量一组样本数据的离散程度,它是通过计算所有数据与样本均值的“偏差平方的平均值”来实现的.即样本的方差 样本方差反应了这组数据的波动情况.随机变量的离散程度能否用可能取值与均值的“偏差平方的平均值”来度量呢? 设离散型随机变量X的分布列如下: X…P…
因为X取每个值的概率不尽相同,而偏差平方关于取值概率的加权平均为 [师生互动] 师:因材施教,根据学生预习的结果,引导下一步教学发挥学生的主观能动性,暴露学生思维,教师精准指导,从而建立方差的概念,发展学生逻辑推理、数学运算、数学抽象和数学建模的核心素养. 3.环节三:得出离散型随机变量方差的概念 一般地,若离散型随机变量X的概率分布列为: Xx1x2…xnPp1p2…pn
则称 为随机变量X的方差,称为随机变量X的标准差。 师:随机变量的方差与标准差都反映了随机变量取值的稳定与波动,集中与分散的程度.那是方差越大越稳定吗? 生:加深学方差或标准差越小,随机变量的取值越集中;方差或标准差越大,随机变量的取值越分散. 4.环节四:课堂练习 例1: 已知随机变量X的分布列如下 X0124P0.10.20.40.1
求D(X) 解: 例2 投资A、B两种股票,每股收益的分布列分别如表1和表2所示: 表1 股票A收益的分布列 表2 股票B收益的分布列 (1)投资哪种股票的期望收益大? 解:股票A和股票B投资收益的期望分别为 因为,所以投资股票A的期望收益较大 (2)投资哪种股票的风险高? 解:股票A和股票B投资收益的方差分别为 D D 因为相差不大,且D,所以投资股票A的风险更大. 【设计意图】通过典例剖析,让学生体会方差的一般方法,加深学生对方差的理解和运用,感受数学模型在数学应用中的价值。发展学生逻辑推理,直观想象、数学抽象和数学运算的核心素养。 5.环节五:课堂小结 1、离散型随机变量的方差 2、利用均值和方差的意义解决实际问题的步骤 (1)比较均值. (2)在均值相等或接近的情况下计算方差 (3)得出结论.方差越小结果越稳定 6.环节六:作业布置 7.环节七:教学反思
