常考专题:解决问题(1-4单元)-小学数学五年级下册浙教版(含解析)
文档属性
| 名称 | 常考专题:解决问题(1-4单元)-小学数学五年级下册浙教版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-10 21:38:44 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
常考专题:解决问题(1-4单元)-小学数学五年级下册浙教版
1.孙悟空、猪八戒、沙僧吃一块蛋糕,已知孙悟空吃了这块蛋糕的,猪八戒吃了这块蛋糕的,沙僧吃了这块蛋糕的。谁吃的最多?
2.五(1)班第一学习小组的同学在玩摸球游戏。
(1)从图中可以知道,第一学习小组的女生和男生分别有多少人?
(2)女生人数是男生的几分之几?
(3)男生人数占第一学习小组人数的几分之几?
(4)你还能用分数表示什么?请写出一个分数,再说明这个分数表示什么。
3.一筐胡萝卜有24个,小白兔吃了这筐胡萝卜的,小白兔吃了多少个胡萝卜?
4.食品店运来一些面包,如果每2个装一袋,每3个装一袋,每5个装一袋,都能正好装完,这些面包可能有多少个?(面包个数在50-80之间)
5.2021年端午节到来之际,为了弘扬传统文化,实验小学开展了“我们的节日——端午”主题活动。其中五年级参加划旱地龙舟的学生在20人~30人之间,赛前预演时,无论4人一组或6人一组都剩余2人,请问五年级参加划旱地龙舟的学生有多少人?
6.五(1)班在男生24人,女生20人。体育课上,老师要把男女生分别分小组活动,但每组的人数都要相等,每组最多应是几人?一共可分成多少个小组?
7.五年级(1)、(2)、(3)班要完成大扫除任务。五(1)班来了54人,五(2)班来了48人,五(3)班来了42人。如果把三个班的学生分别分成若干小组,要使三个班每个小组的人数相同,每班可以分成几组?
8.工程队铺一条路,如果每天铺60米,12天铺完。如果9天铺完,每天要铺多少米?
9.甲、乙两人合作为400米的环形花坛铺设草坪,两人同时从同一地点背向而行各自铺设,最初甲铺设草坪的速度比乙快,后来乙用了10分钟去调换工具,回来继续铺设,但工作效率比原来提高了一倍。结果从甲、乙开始铺设时间算起,经过1小时,就完成了铺设草坪工作,并且两人铺设的草坪距离一样长,问乙换了工具后又工作了多少分钟?
10.学校有槐树15棵,杨树的棵数是槐树的,并且又是柳树的,柳树有多少棵?
11.蜂鸟是目前已知最小的鸟,也是唯一能倒飞的鸟。一只蜂鸟平均每分钟飞行千米,分能飞行多少千米?
12.李叔叔原来的体重是80千克,坚持体育锻炼后,体重减轻了,李叔叔的体重减轻了多少千克?
13.五年级植树336棵,六年级植树的棵数比五年级多,五年级比六年级少植树多少棵?
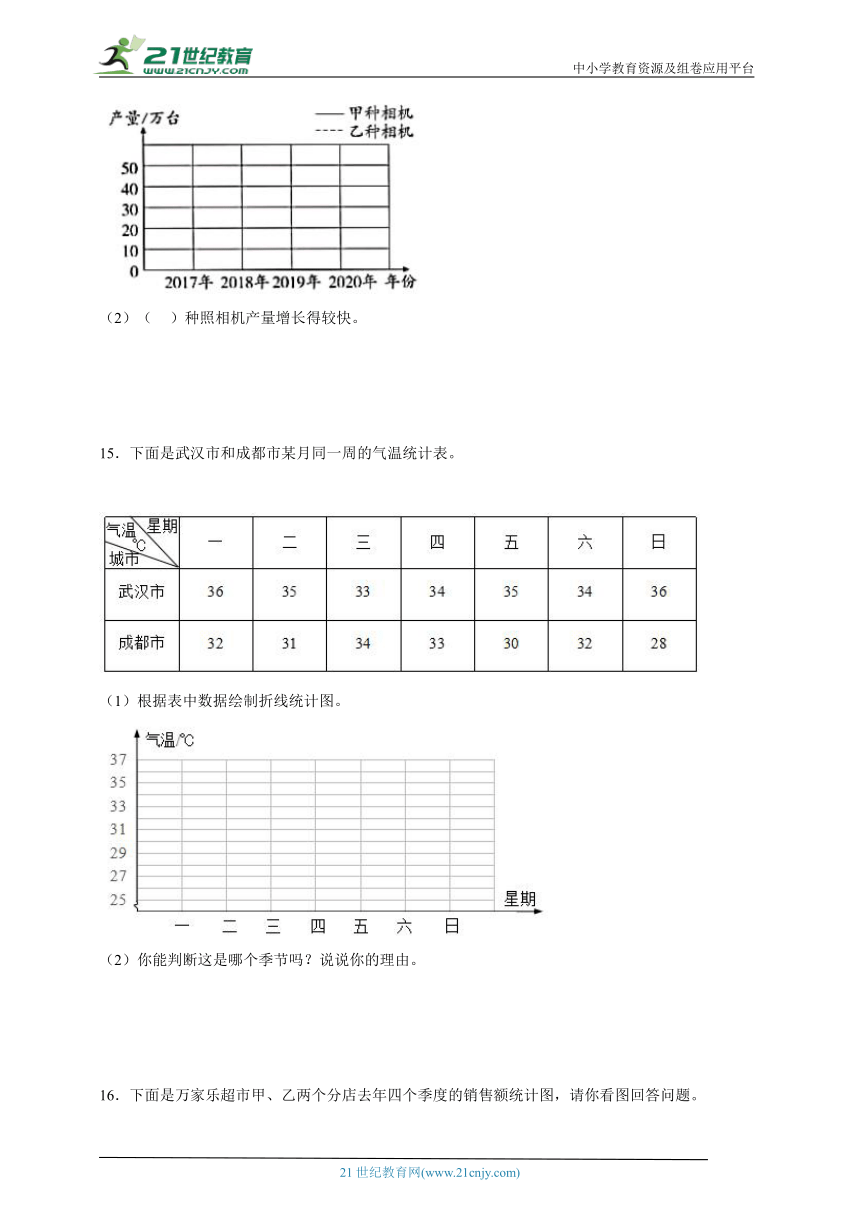
14.下面是某数码照相机厂2017~2020年两种型号照相机的产量统计表。(单位:万台)
年份 2017 2018 2019 2020
甲种照相机 15 23 30 40
乙种照相机 10 18 25 45
(1)根据表中的数据,完成下面的折线统计图。
某数码照相机厂2017-2020年两种型号照相机的产量统计图
(2)( )种照相机产量增长得较快。
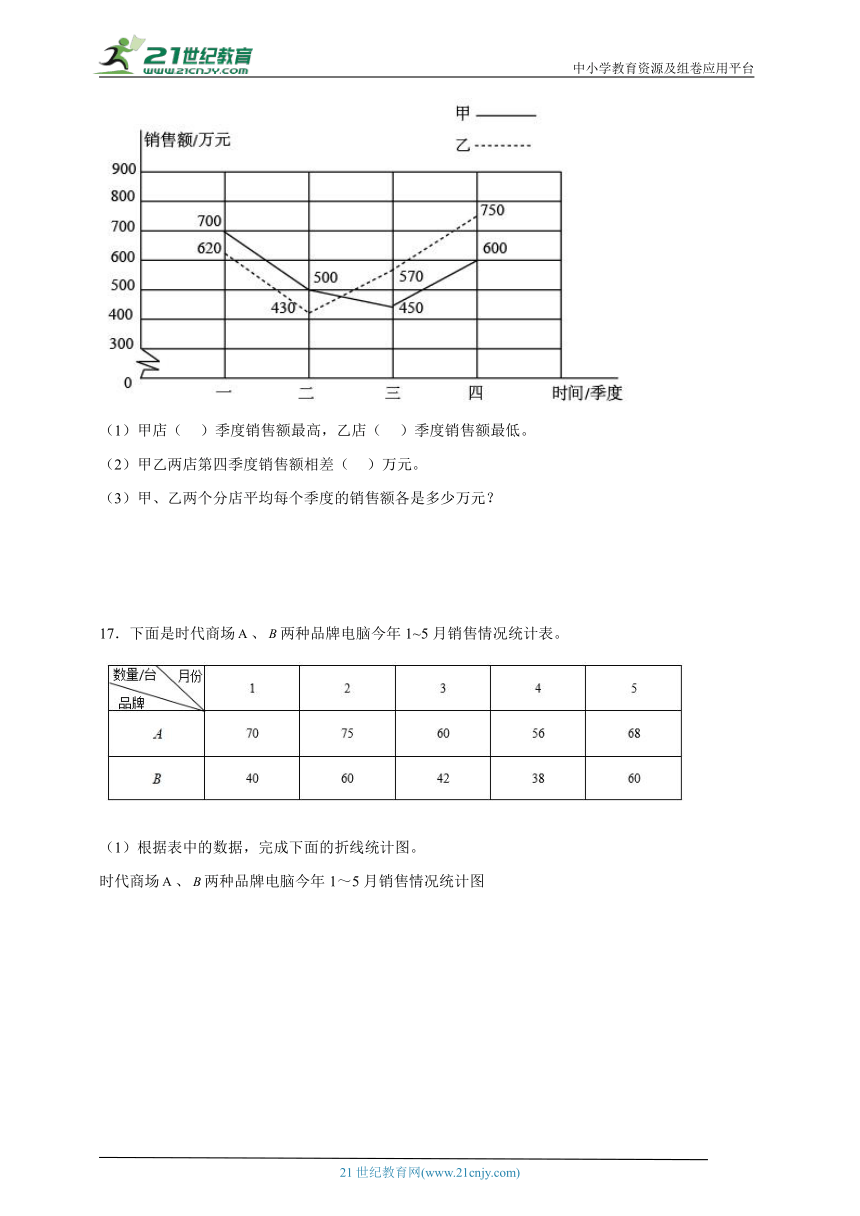
15.下面是武汉市和成都市某月同一周的气温统计表。
(1)根据表中数据绘制折线统计图。
(2)你能判断这是哪个季节吗?说说你的理由。
16.下面是万家乐超市甲、乙两个分店去年四个季度的销售额统计图,请你看图回答问题。
(1)甲店( )季度销售额最高,乙店( )季度销售额最低。
(2)甲乙两店第四季度销售额相差( )万元。
(3)甲、乙两个分店平均每个季度的销售额各是多少万元?
17.下面是时代商场、两种品牌电脑今年1~5月销售情况统计表。
(1)根据表中的数据,完成下面的折线统计图。
时代商场、两种品牌电脑今年1~5月销售情况统计图
(2)观察统计图并回答以下问题:
①、两种品牌电脑( )月的销售量差距最大,相差( )台。
②( )品牌电脑今年前5个月的销售量较多。
③如果你是时代商场的经理,对于下半年的进货有什么想法?
18.一个密封的长方体容器如图,长4分米、宽1分米、高2分米,里面水深16厘米。如果以这个容器的左侧面为底放在桌上。
(1)这时水深多少分米?
(2)此时,水与容器接触的面积是多少平方分米?
19.教学楼门前有一根长方体柱子,高3.6m,底面是边长0.4m的正方形。如果要给这根柱子的四周刷油漆,每平方米需要油漆0.3kg,一共需要油漆多少千克?
20.用硬纸板制作一个长方体无盖收纳盒,长20cm、宽10cm、高15m。制成这个收纳盒至少需要多少平方分米?
21.一个长方体和一个正方体的棱长总和相等。已知长方体的长是4cm、宽是3cm、高是5cm。
(1)正方体的棱长是多少厘米?
(2)正方体的表面积是多少平方厘米?
(3)正方体的体积是多少立方厘米?
22.一块长方形铁皮,长40cm,宽35cm。从四个角各切掉边长为5cm的正方形,然后折成一个盒子,这个盒子的容积是多少毫升?(铁皮厚度忽略不计)
参考答案:
1.沙僧
【分析】根据异分母分数比较大小,要先通分,再比较大小即可解答。
【详解】
因为
所以
答:沙僧吃的最多。
【点睛】本题主要考查异分母分数比较大小,要先通分,再比较大小。
2.(1)女生:3人;男生:4人
(2)
(3)
(4)见详解
【分析】(1)根据图数出第一学习小组的女生和男生的人数即可;
(2)用女生人数除以男生人数,结果用分数表示即可;
(3)用男生人数除以第一学习小组总人数,结果用分数表示即可;
(4)根据分数的意义,随意举一个分数,写出它的意义即可。
【详解】(1)第一学习小组的女生有3人,男生有4人。
(2)3÷4=
答:女生人数是男生的。
(3)4÷(3+4)
=4÷7
=
答:男生人数占第一学习小组人数的。
(4)例如
把一个整体平均分成8份,其中的7份表示。(答案不唯一)
【点睛】本题主要考查分数的意义以及一个数是另一个数的几分之几,用一个数÷另一个数。
3.3个
【分析】因为小白兔吃了这筐胡萝卜的,要求小白兔吃得个数就是把这筐胡萝卜平均分成8份,求出1份是多少,据此解答。
【详解】24÷8=3(个)
答:小白兔吃了3个胡萝卜。
【点睛】此题关键掌握分数的简单应用。
4.60个
【分析】根据题意,如果每2个装一袋,每3个装一袋,每5个装一袋,都能正好装完,就是求2、3、5的公倍数,而且在50-80之间。
【详解】2×3×5=30(个)
30×2=60(个)
答:这些面包可能有60个。
【点睛】本题主要考查公倍数的求法及运用。
5.26人
【分析】根据题意,五年级参加旱地龙舟的学生人数在20人~30人之间,无论4人或6人一组都省2人,求出4和6的公倍数,在20~30之间,求出倍数再加上2,就是参加旱地龙舟的学生人数。
【详解】4的倍数:4、8、12、16、20、24、28、32……
6的倍数:6、12、18、24、30……
4和6在20~30之间的倍数是24
24+2=26(人)
答:五年级参加旱地龙舟的学生有26人。
【点睛】本题考查两个数的公倍数的求法。
6.4人;11组
【分析】由男女生各自分组,要使每组的人数相同,可知每组的人数是男生和女生人数的公因数,要求每组多有多少人,就是每组的人数是男生和女生人数的最大公因数;求可以分成多少个小组,只要用男、女生人数分别除以每组的人数再相加即可。
【详解】24=2×2×2×3
20=2×2×5
所以24和20的最大公因数是:4
即每组最多有4人
男生分的组数:24÷4=6(组)
女生分得组数:20÷4=5(组)
6+5=11(组)
答:每组最多有4人,可以分成11个小组.
【点睛】解答本题关键是理解:每组的人数是男生和女生人数的公因数,要求每组最多有多少人,就是每组的人数是男生和女生人数的最大公因数。
7.2组、3组或6组
【分析】求出三个班人数除1之外的公因数就是可以分成的组数。
【详解】54的因数有:1、2、3、6、9、18、27、54;
48的因数有:1、2、3、4、6、8、12、16、24、48;
42的因数有:1、2、3、6、7、14、21、42。
54、48、42的公因数有2、3、6。
答:每班可以分成2组、3组或6组。
【点睛】解决此题关键是把问题转化成求三个数的公因数,再根据求三个数的公因数的方法解答即可。
8.80米
【分析】用计划每天铺的米数乘时间,求出总长度,再用总长度除以实际时间,即可求出实际每天铺的米数。
【详解】60×12÷9
=720÷9
=80(米)
答:每天要铺80米。
【点睛】明确总长度不变,求出总长度是解答本题的关键。
9.30分钟
【分析】设乙原来铺设速度为v,最初甲铺设草坪的速度比乙快,则甲的铺设速度是乙的1+,又因为甲1小时即60分钟清理了400÷2=200米,由此可得方程:60×(1+)v=200,求出v=2.5米/每分钟,乙后来回来继续铺设,但工作效率比原来提高了一倍,即为每分钟2.5×(1+1)米,再设乙换工具后又工作了x分钟,则乙按原速度铺设了60﹣10﹣x分钟,铺设了(60﹣10﹣x)×2.5米,后来铺设了2.5×(1+1)x米,由此可得方程:(60﹣10﹣x)×2.5+2.5×(1+1)x=400÷2,解答即可。
【详解】1小时=60分钟
解:设乙原来铺设速度为v。
60×(1+ )v=400÷2
60×v=400÷2
80v÷80=200÷80
v=2.5
解:设乙换工具后又铺设了x分钟。
(60﹣10﹣x)×2.5+2.5×(1+1)x=400÷2
(50﹣x)×2.5+2.5×2x=200
125-2.5x+5x=200
125+2.5x-125=200-125
2.5x÷2.5=75÷2.5
x=30
答:乙换了工具后又工作了30分钟。
【点睛】用方程解决问题的关键是找到等量关系。
10.35棵
【分析】根据题意,杨树的棵数是槐树的,用槐树的棵数×,求出杨树的棵数;杨树的棵数又是柳树的,用杨树的棵数÷,求出柳树的棵数,据此解答。
【详解】15×÷
=10÷
=10×
=35(棵)
答:柳树有35棵。
【点睛】利用求一个数的几分之几是多少,已知一个数的几分之几是多少,求这个数的知识进行解答。
11.千米
【分析】由题意知:用速度乘时间得到飞行总路程。据此解答。
【详解】×=(千米)
答:分能飞行千米。
【点睛】本题主要考查了简单的行程问题,解答此题的关键是明确:求一个数的几分之几是多少,用乘法计算。
12.10千克
【分析】把原来的体重看作单位“1” , 坚持体育锻炼后,体重减轻了,求体重减轻了多少千克,也就是求80千克的是多少千克。根据一个数乘分数的意义解答。
【详解】(千克)
答:李叔叔的体重减轻了10千克。
【点睛】此题考查的目的是理解掌握一个数乘分数的意义及应用。
13.42棵
【分析】把五年级植数的棵数看作“单位1”,“六年级植树的棵数比五年级多”意思就是:六年级植树的棵数比五年级多植的棵数占五年级的,也可以说是,五年级比六年级少植的棵数占五年级的;要求最后的问题,可以用乘法解答;也可以先求出六年级植树的棵数,再减去五年级的棵数。
【详解】336×=42(棵)
或:336×(1+)﹣336
=378﹣336
=42(棵)
答:五年级比六年级少植树42棵。
【点睛】此题是属于“求一个数的几分之几是多少”的分数应用题,看清“单位1”,理清谁比谁多,谁比谁少再进行解答。
14.(1)见详解
(2)乙
【分析】(1)根据统计表完成统计图即可;
(2)根据统计图可知,从2017~2019年,两种照相机的增长速度一样,从2019~2020年,乙种照相机明显比甲种照相机增长快,据此可知,乙种照相机产量增长得较快。
【详解】(1)折线统计图如下:
某数码照相机厂2017~2020年两种型号照相机的产量统计图
(2)乙种照相机产量增长得较快。
【点睛】熟练掌握折线统计图的画法,读懂统计图中的数学信息是解答本题的关键。
15.(1)见详解;
(2)从统计图中,可以判断这是夏季,因为气温比较高。
【分析】(1)根据统计表中的信息先描点,再依次连接各个点即可;
(2)观察统计表中的数据,联系生活实际,这些数据都比较高,应属于夏季。
【详解】(1)据分析可作图如下:
(2)从统计图中,可以判断这是夏季,因为气温比较高。
【点睛】具有一定的生活经验,掌握画折线统计图的方法,先描点再连线,这是解决此题的关键。
16.(1)一;二
(2)150
(3)562.5万元;592.5万元
【分析】(1)观察统计图,数据点位置越高表示销售额越高,数据点位置越低表示销售额越低;
(2)找到第四季度甲乙两店销售额,求差即可;
(3)根据平均数=总数÷份数,列式解答即可。
【详解】(1)甲店一季度销售额最高,乙店二季度销售额最低。
(2)750-600=150(万元)
(3)(700+500+450+600)÷4
=2250÷4
=562.5(万元)
(620+430+570+750)÷4
=2370÷4
=592.5(万元)
答:甲、乙两个分店平均每个季度的销售额各是562.5万元,592.5万元。
【点睛】折线统计图的特点不仅能看清数量的多少,还能通过折线的上升和下降表示数量的增减变化情况。复式折线统计图表示2个及以上的量的增减变化情况。
17.(1)见详解
(2)①1;30;
②A;
③对于下半年进货我会多进一些A品牌的电脑,因为前5个月A品牌电脑销量最多,说明A品牌更受消费者欢迎,故所获利润也会更大。
【分析】(1)由统计表作折线统计图时,先找到横坐标的月份数,再根据月份数往上找出对应的销售量的点,依次连接每个月的销量的点,即可得出折线统计图。
(2)根据统计表中,可得出答案;通过折线统计图看出A品牌的电脑销量更好,据得出答案。
【详解】(1)依次再统计图中找出每个月的销量,再连接各点即可做出折线统计图;
(2)①由折线统计图中可看出,1月份、两种品牌电脑的销售量差距最大,相差(台);
② 由统计表中得到,A品牌电脑今年前5个月的销售量较多;
③对于下半年进货我会多进一些A品牌的电脑,因为前5个月A品牌电脑销量最多,说明A品牌更受消费者欢迎,故所获利润也会更大。
【点睛】本题主要考查的是统计图的作法及复式折线统计图,解题的关键是根据统计表作出复式折线统计图。
18.(1)3.2分米
(2)21.2平方分米
【分析】(1)根据长方体的体积公式V=abh,求出长方体容器内水的体积,由于容器内水的体积不变,把容器的左面作为底面,所以用水的体积除以左面那个面的底面积就是水面的高度;
(2)水与容器的接触面的面积就是长2分米,宽1分米,高为此时水深的长方体5个面的面积,缺少上面,根据长方体的表面积解答即可。
【详解】16厘米=1.6分米
(1)4×1×1.6=6.4(立方分米)
6.4÷(2×1)
=6.4÷2
=3.2(分米)
答:这时水深3.2分米。
(2)2×1+2×3.2×2+1×3.2×2
=2+12.8+6.4
=21.2(平方分米)
答:水与容器的接触面的面积是21.2平方分米。
【点睛】解答此题应抓住水的体积不变,用水的体积除以长方体容器的底面积(左面那个面的面积),就是水面的高度。
19.1.728千克
【分析】当长方体的底面是正方形时,则其前后面和左右面完全相同,用3.6×0.4求出一个面的面积,再乘4即可求出前后左右四个面的面积,再乘每平方米需要油漆的质量即可。
【详解】3.6×0.4×4×0.3
=5.76×0.3
=1.728(千克);
答:一共需要油漆1.728千克。
【点睛】本题较易,关键是先求出前后左右四个面的面积和。
20.11平方分米
【分析】根据题意可知,就是求长方体前后面、左右面和底面的面积和,据此解答即可。
【详解】20×10+20×15×2+10×15×2
=200+600+300
=1100(平方厘米)
1100平方厘米=11平方分米
答:制成这个收纳盒至少需要11平方分米。
【点睛】熟练掌握长方体表面积的计算公式是解答本题的关键,要注意单位。
21.(1)4厘米;
(2)96平方厘米;
(3)64立方厘米
【分析】(1)长方体的棱长=(长+宽+高)×4代入数据求出长方体的棱长也就是正方体的棱长总和,再根据正方体棱长=棱长总和÷12,求出正方体棱长;
(2)将数据代入正方体表面积公式:S=6a2,计算即可;
(3)将数据代入正方体体积公式:V=a3,计算即可。
【详解】(1)(4+3+5)×4÷12
=12×4÷12
=4(厘米)
答:正方体的棱长是4厘米。
(2)4×4×6
=16×6
=96(平方厘米)
答:正方体的表面积是96平方厘米。
(3)4×4×4
=16×4
=64(立方厘米)
答:正方体的体积是64立方厘米。
【点睛】本题主要考查正方体棱长总和、表面积、体积公式的灵活应用,求出正方体的棱长是解题的关键。
22.3750毫升
【分析】折成的这个长方体的高是5厘米,长是30厘米,宽是25厘米。据此利用长方体的体积公式,直接列式计算出这个盒子的容积即可。
【详解】(40-5×2)×(35-5×2)×5
=30×25×5
=3750(立方厘米)
3750立方厘米=3750毫升
答:这个盒子的容积是3750毫升。
【点睛】本题考查了长方体的体积,长方体的体积等于长乘宽乘高。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
常考专题:解决问题(1-4单元)-小学数学五年级下册浙教版
1.孙悟空、猪八戒、沙僧吃一块蛋糕,已知孙悟空吃了这块蛋糕的,猪八戒吃了这块蛋糕的,沙僧吃了这块蛋糕的。谁吃的最多?
2.五(1)班第一学习小组的同学在玩摸球游戏。
(1)从图中可以知道,第一学习小组的女生和男生分别有多少人?
(2)女生人数是男生的几分之几?
(3)男生人数占第一学习小组人数的几分之几?
(4)你还能用分数表示什么?请写出一个分数,再说明这个分数表示什么。
3.一筐胡萝卜有24个,小白兔吃了这筐胡萝卜的,小白兔吃了多少个胡萝卜?
4.食品店运来一些面包,如果每2个装一袋,每3个装一袋,每5个装一袋,都能正好装完,这些面包可能有多少个?(面包个数在50-80之间)
5.2021年端午节到来之际,为了弘扬传统文化,实验小学开展了“我们的节日——端午”主题活动。其中五年级参加划旱地龙舟的学生在20人~30人之间,赛前预演时,无论4人一组或6人一组都剩余2人,请问五年级参加划旱地龙舟的学生有多少人?
6.五(1)班在男生24人,女生20人。体育课上,老师要把男女生分别分小组活动,但每组的人数都要相等,每组最多应是几人?一共可分成多少个小组?
7.五年级(1)、(2)、(3)班要完成大扫除任务。五(1)班来了54人,五(2)班来了48人,五(3)班来了42人。如果把三个班的学生分别分成若干小组,要使三个班每个小组的人数相同,每班可以分成几组?
8.工程队铺一条路,如果每天铺60米,12天铺完。如果9天铺完,每天要铺多少米?
9.甲、乙两人合作为400米的环形花坛铺设草坪,两人同时从同一地点背向而行各自铺设,最初甲铺设草坪的速度比乙快,后来乙用了10分钟去调换工具,回来继续铺设,但工作效率比原来提高了一倍。结果从甲、乙开始铺设时间算起,经过1小时,就完成了铺设草坪工作,并且两人铺设的草坪距离一样长,问乙换了工具后又工作了多少分钟?
10.学校有槐树15棵,杨树的棵数是槐树的,并且又是柳树的,柳树有多少棵?
11.蜂鸟是目前已知最小的鸟,也是唯一能倒飞的鸟。一只蜂鸟平均每分钟飞行千米,分能飞行多少千米?
12.李叔叔原来的体重是80千克,坚持体育锻炼后,体重减轻了,李叔叔的体重减轻了多少千克?
13.五年级植树336棵,六年级植树的棵数比五年级多,五年级比六年级少植树多少棵?
14.下面是某数码照相机厂2017~2020年两种型号照相机的产量统计表。(单位:万台)
年份 2017 2018 2019 2020
甲种照相机 15 23 30 40
乙种照相机 10 18 25 45
(1)根据表中的数据,完成下面的折线统计图。
某数码照相机厂2017-2020年两种型号照相机的产量统计图
(2)( )种照相机产量增长得较快。
15.下面是武汉市和成都市某月同一周的气温统计表。
(1)根据表中数据绘制折线统计图。
(2)你能判断这是哪个季节吗?说说你的理由。
16.下面是万家乐超市甲、乙两个分店去年四个季度的销售额统计图,请你看图回答问题。
(1)甲店( )季度销售额最高,乙店( )季度销售额最低。
(2)甲乙两店第四季度销售额相差( )万元。
(3)甲、乙两个分店平均每个季度的销售额各是多少万元?
17.下面是时代商场、两种品牌电脑今年1~5月销售情况统计表。
(1)根据表中的数据,完成下面的折线统计图。
时代商场、两种品牌电脑今年1~5月销售情况统计图
(2)观察统计图并回答以下问题:
①、两种品牌电脑( )月的销售量差距最大,相差( )台。
②( )品牌电脑今年前5个月的销售量较多。
③如果你是时代商场的经理,对于下半年的进货有什么想法?
18.一个密封的长方体容器如图,长4分米、宽1分米、高2分米,里面水深16厘米。如果以这个容器的左侧面为底放在桌上。
(1)这时水深多少分米?
(2)此时,水与容器接触的面积是多少平方分米?
19.教学楼门前有一根长方体柱子,高3.6m,底面是边长0.4m的正方形。如果要给这根柱子的四周刷油漆,每平方米需要油漆0.3kg,一共需要油漆多少千克?
20.用硬纸板制作一个长方体无盖收纳盒,长20cm、宽10cm、高15m。制成这个收纳盒至少需要多少平方分米?
21.一个长方体和一个正方体的棱长总和相等。已知长方体的长是4cm、宽是3cm、高是5cm。
(1)正方体的棱长是多少厘米?
(2)正方体的表面积是多少平方厘米?
(3)正方体的体积是多少立方厘米?
22.一块长方形铁皮,长40cm,宽35cm。从四个角各切掉边长为5cm的正方形,然后折成一个盒子,这个盒子的容积是多少毫升?(铁皮厚度忽略不计)
参考答案:
1.沙僧
【分析】根据异分母分数比较大小,要先通分,再比较大小即可解答。
【详解】
因为
所以
答:沙僧吃的最多。
【点睛】本题主要考查异分母分数比较大小,要先通分,再比较大小。
2.(1)女生:3人;男生:4人
(2)
(3)
(4)见详解
【分析】(1)根据图数出第一学习小组的女生和男生的人数即可;
(2)用女生人数除以男生人数,结果用分数表示即可;
(3)用男生人数除以第一学习小组总人数,结果用分数表示即可;
(4)根据分数的意义,随意举一个分数,写出它的意义即可。
【详解】(1)第一学习小组的女生有3人,男生有4人。
(2)3÷4=
答:女生人数是男生的。
(3)4÷(3+4)
=4÷7
=
答:男生人数占第一学习小组人数的。
(4)例如
把一个整体平均分成8份,其中的7份表示。(答案不唯一)
【点睛】本题主要考查分数的意义以及一个数是另一个数的几分之几,用一个数÷另一个数。
3.3个
【分析】因为小白兔吃了这筐胡萝卜的,要求小白兔吃得个数就是把这筐胡萝卜平均分成8份,求出1份是多少,据此解答。
【详解】24÷8=3(个)
答:小白兔吃了3个胡萝卜。
【点睛】此题关键掌握分数的简单应用。
4.60个
【分析】根据题意,如果每2个装一袋,每3个装一袋,每5个装一袋,都能正好装完,就是求2、3、5的公倍数,而且在50-80之间。
【详解】2×3×5=30(个)
30×2=60(个)
答:这些面包可能有60个。
【点睛】本题主要考查公倍数的求法及运用。
5.26人
【分析】根据题意,五年级参加旱地龙舟的学生人数在20人~30人之间,无论4人或6人一组都省2人,求出4和6的公倍数,在20~30之间,求出倍数再加上2,就是参加旱地龙舟的学生人数。
【详解】4的倍数:4、8、12、16、20、24、28、32……
6的倍数:6、12、18、24、30……
4和6在20~30之间的倍数是24
24+2=26(人)
答:五年级参加旱地龙舟的学生有26人。
【点睛】本题考查两个数的公倍数的求法。
6.4人;11组
【分析】由男女生各自分组,要使每组的人数相同,可知每组的人数是男生和女生人数的公因数,要求每组多有多少人,就是每组的人数是男生和女生人数的最大公因数;求可以分成多少个小组,只要用男、女生人数分别除以每组的人数再相加即可。
【详解】24=2×2×2×3
20=2×2×5
所以24和20的最大公因数是:4
即每组最多有4人
男生分的组数:24÷4=6(组)
女生分得组数:20÷4=5(组)
6+5=11(组)
答:每组最多有4人,可以分成11个小组.
【点睛】解答本题关键是理解:每组的人数是男生和女生人数的公因数,要求每组最多有多少人,就是每组的人数是男生和女生人数的最大公因数。
7.2组、3组或6组
【分析】求出三个班人数除1之外的公因数就是可以分成的组数。
【详解】54的因数有:1、2、3、6、9、18、27、54;
48的因数有:1、2、3、4、6、8、12、16、24、48;
42的因数有:1、2、3、6、7、14、21、42。
54、48、42的公因数有2、3、6。
答:每班可以分成2组、3组或6组。
【点睛】解决此题关键是把问题转化成求三个数的公因数,再根据求三个数的公因数的方法解答即可。
8.80米
【分析】用计划每天铺的米数乘时间,求出总长度,再用总长度除以实际时间,即可求出实际每天铺的米数。
【详解】60×12÷9
=720÷9
=80(米)
答:每天要铺80米。
【点睛】明确总长度不变,求出总长度是解答本题的关键。
9.30分钟
【分析】设乙原来铺设速度为v,最初甲铺设草坪的速度比乙快,则甲的铺设速度是乙的1+,又因为甲1小时即60分钟清理了400÷2=200米,由此可得方程:60×(1+)v=200,求出v=2.5米/每分钟,乙后来回来继续铺设,但工作效率比原来提高了一倍,即为每分钟2.5×(1+1)米,再设乙换工具后又工作了x分钟,则乙按原速度铺设了60﹣10﹣x分钟,铺设了(60﹣10﹣x)×2.5米,后来铺设了2.5×(1+1)x米,由此可得方程:(60﹣10﹣x)×2.5+2.5×(1+1)x=400÷2,解答即可。
【详解】1小时=60分钟
解:设乙原来铺设速度为v。
60×(1+ )v=400÷2
60×v=400÷2
80v÷80=200÷80
v=2.5
解:设乙换工具后又铺设了x分钟。
(60﹣10﹣x)×2.5+2.5×(1+1)x=400÷2
(50﹣x)×2.5+2.5×2x=200
125-2.5x+5x=200
125+2.5x-125=200-125
2.5x÷2.5=75÷2.5
x=30
答:乙换了工具后又工作了30分钟。
【点睛】用方程解决问题的关键是找到等量关系。
10.35棵
【分析】根据题意,杨树的棵数是槐树的,用槐树的棵数×,求出杨树的棵数;杨树的棵数又是柳树的,用杨树的棵数÷,求出柳树的棵数,据此解答。
【详解】15×÷
=10÷
=10×
=35(棵)
答:柳树有35棵。
【点睛】利用求一个数的几分之几是多少,已知一个数的几分之几是多少,求这个数的知识进行解答。
11.千米
【分析】由题意知:用速度乘时间得到飞行总路程。据此解答。
【详解】×=(千米)
答:分能飞行千米。
【点睛】本题主要考查了简单的行程问题,解答此题的关键是明确:求一个数的几分之几是多少,用乘法计算。
12.10千克
【分析】把原来的体重看作单位“1” , 坚持体育锻炼后,体重减轻了,求体重减轻了多少千克,也就是求80千克的是多少千克。根据一个数乘分数的意义解答。
【详解】(千克)
答:李叔叔的体重减轻了10千克。
【点睛】此题考查的目的是理解掌握一个数乘分数的意义及应用。
13.42棵
【分析】把五年级植数的棵数看作“单位1”,“六年级植树的棵数比五年级多”意思就是:六年级植树的棵数比五年级多植的棵数占五年级的,也可以说是,五年级比六年级少植的棵数占五年级的;要求最后的问题,可以用乘法解答;也可以先求出六年级植树的棵数,再减去五年级的棵数。
【详解】336×=42(棵)
或:336×(1+)﹣336
=378﹣336
=42(棵)
答:五年级比六年级少植树42棵。
【点睛】此题是属于“求一个数的几分之几是多少”的分数应用题,看清“单位1”,理清谁比谁多,谁比谁少再进行解答。
14.(1)见详解
(2)乙
【分析】(1)根据统计表完成统计图即可;
(2)根据统计图可知,从2017~2019年,两种照相机的增长速度一样,从2019~2020年,乙种照相机明显比甲种照相机增长快,据此可知,乙种照相机产量增长得较快。
【详解】(1)折线统计图如下:
某数码照相机厂2017~2020年两种型号照相机的产量统计图
(2)乙种照相机产量增长得较快。
【点睛】熟练掌握折线统计图的画法,读懂统计图中的数学信息是解答本题的关键。
15.(1)见详解;
(2)从统计图中,可以判断这是夏季,因为气温比较高。
【分析】(1)根据统计表中的信息先描点,再依次连接各个点即可;
(2)观察统计表中的数据,联系生活实际,这些数据都比较高,应属于夏季。
【详解】(1)据分析可作图如下:
(2)从统计图中,可以判断这是夏季,因为气温比较高。
【点睛】具有一定的生活经验,掌握画折线统计图的方法,先描点再连线,这是解决此题的关键。
16.(1)一;二
(2)150
(3)562.5万元;592.5万元
【分析】(1)观察统计图,数据点位置越高表示销售额越高,数据点位置越低表示销售额越低;
(2)找到第四季度甲乙两店销售额,求差即可;
(3)根据平均数=总数÷份数,列式解答即可。
【详解】(1)甲店一季度销售额最高,乙店二季度销售额最低。
(2)750-600=150(万元)
(3)(700+500+450+600)÷4
=2250÷4
=562.5(万元)
(620+430+570+750)÷4
=2370÷4
=592.5(万元)
答:甲、乙两个分店平均每个季度的销售额各是562.5万元,592.5万元。
【点睛】折线统计图的特点不仅能看清数量的多少,还能通过折线的上升和下降表示数量的增减变化情况。复式折线统计图表示2个及以上的量的增减变化情况。
17.(1)见详解
(2)①1;30;
②A;
③对于下半年进货我会多进一些A品牌的电脑,因为前5个月A品牌电脑销量最多,说明A品牌更受消费者欢迎,故所获利润也会更大。
【分析】(1)由统计表作折线统计图时,先找到横坐标的月份数,再根据月份数往上找出对应的销售量的点,依次连接每个月的销量的点,即可得出折线统计图。
(2)根据统计表中,可得出答案;通过折线统计图看出A品牌的电脑销量更好,据得出答案。
【详解】(1)依次再统计图中找出每个月的销量,再连接各点即可做出折线统计图;
(2)①由折线统计图中可看出,1月份、两种品牌电脑的销售量差距最大,相差(台);
② 由统计表中得到,A品牌电脑今年前5个月的销售量较多;
③对于下半年进货我会多进一些A品牌的电脑,因为前5个月A品牌电脑销量最多,说明A品牌更受消费者欢迎,故所获利润也会更大。
【点睛】本题主要考查的是统计图的作法及复式折线统计图,解题的关键是根据统计表作出复式折线统计图。
18.(1)3.2分米
(2)21.2平方分米
【分析】(1)根据长方体的体积公式V=abh,求出长方体容器内水的体积,由于容器内水的体积不变,把容器的左面作为底面,所以用水的体积除以左面那个面的底面积就是水面的高度;
(2)水与容器的接触面的面积就是长2分米,宽1分米,高为此时水深的长方体5个面的面积,缺少上面,根据长方体的表面积解答即可。
【详解】16厘米=1.6分米
(1)4×1×1.6=6.4(立方分米)
6.4÷(2×1)
=6.4÷2
=3.2(分米)
答:这时水深3.2分米。
(2)2×1+2×3.2×2+1×3.2×2
=2+12.8+6.4
=21.2(平方分米)
答:水与容器的接触面的面积是21.2平方分米。
【点睛】解答此题应抓住水的体积不变,用水的体积除以长方体容器的底面积(左面那个面的面积),就是水面的高度。
19.1.728千克
【分析】当长方体的底面是正方形时,则其前后面和左右面完全相同,用3.6×0.4求出一个面的面积,再乘4即可求出前后左右四个面的面积,再乘每平方米需要油漆的质量即可。
【详解】3.6×0.4×4×0.3
=5.76×0.3
=1.728(千克);
答:一共需要油漆1.728千克。
【点睛】本题较易,关键是先求出前后左右四个面的面积和。
20.11平方分米
【分析】根据题意可知,就是求长方体前后面、左右面和底面的面积和,据此解答即可。
【详解】20×10+20×15×2+10×15×2
=200+600+300
=1100(平方厘米)
1100平方厘米=11平方分米
答:制成这个收纳盒至少需要11平方分米。
【点睛】熟练掌握长方体表面积的计算公式是解答本题的关键,要注意单位。
21.(1)4厘米;
(2)96平方厘米;
(3)64立方厘米
【分析】(1)长方体的棱长=(长+宽+高)×4代入数据求出长方体的棱长也就是正方体的棱长总和,再根据正方体棱长=棱长总和÷12,求出正方体棱长;
(2)将数据代入正方体表面积公式:S=6a2,计算即可;
(3)将数据代入正方体体积公式:V=a3,计算即可。
【详解】(1)(4+3+5)×4÷12
=12×4÷12
=4(厘米)
答:正方体的棱长是4厘米。
(2)4×4×6
=16×6
=96(平方厘米)
答:正方体的表面积是96平方厘米。
(3)4×4×4
=16×4
=64(立方厘米)
答:正方体的体积是64立方厘米。
【点睛】本题主要考查正方体棱长总和、表面积、体积公式的灵活应用,求出正方体的棱长是解题的关键。
22.3750毫升
【分析】折成的这个长方体的高是5厘米,长是30厘米,宽是25厘米。据此利用长方体的体积公式,直接列式计算出这个盒子的容积即可。
【详解】(40-5×2)×(35-5×2)×5
=30×25×5
=3750(立方厘米)
3750立方厘米=3750毫升
答:这个盒子的容积是3750毫升。
【点睛】本题考查了长方体的体积,长方体的体积等于长乘宽乘高。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
