随机抽样[下学期]
图片预览




文档简介
课件11张PPT。2019/3/15第二章 统 计2019/3/15第二章 统 计2.1 随机抽样
2.2 用样本估计总体
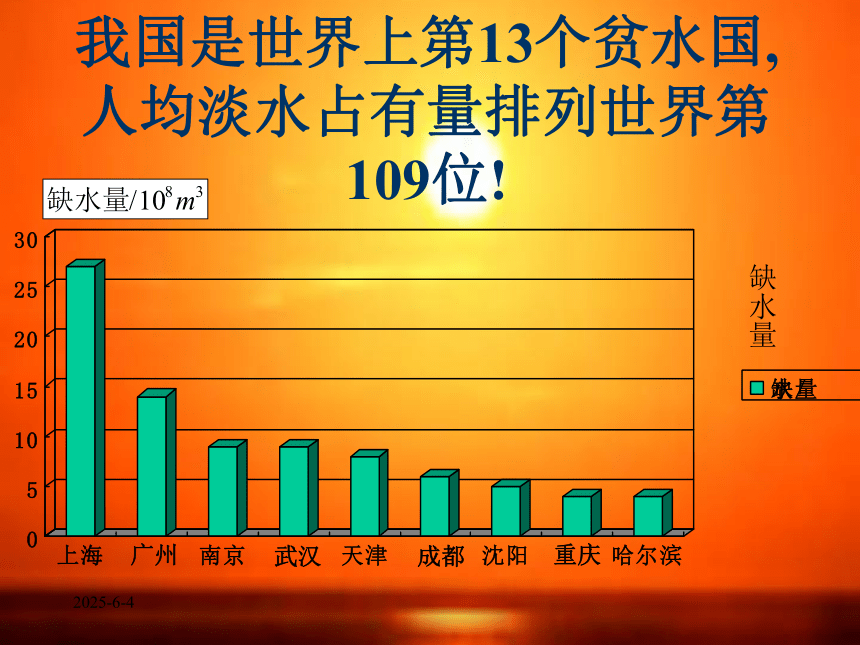
2.3 变量间的相关关系2019/3/15 我国是世界上第13个贫水国, 人均淡水占有量排列世界第109位! 2019/3/15 章引:
我们生活在一个数字化的时代,时刻都在与数据打交道,例如,产品的合格率,农作物的产量,商品的销售量,当地的气温,自然资源,就业状况,电视台的收视率,你知道这些数据是怎么来的吗?实际上它们是通过调查获得的.怎样调查呢?是对考察对象进行全面调查吗?例如,为了了解计算器的使用寿命,我们能将它们一一测试吗?很明显,这不可能,也没必要.实践中,由于所考察的总体中的个体数往往很多,而且许多考察具有破坏性,因此我们通常只考察总体中的一个样本,通过样本来了解总体的情况.进一步从节约费用的角度考虑,在保证样本估计总体达到一定精度的前提下,样本中包含的个体数越少越好.2019/3/15 于是,如何设计抽样方法,使抽取得样本能够真正代表总体,就成为我们要关注的一个关键问题.否则,如果样本的代表性不好,那么对总体的判断就会出现错误.
那么,怎样从总体中抽取样本呢?如何表示样本数据呢?如何从样本数据中提取基本信息(样本分布,样本数字特征等),来推断总体的情况呢?2019/3/15探究: 假设你作为一名食品卫生工作人员,要对食品店内的一批小包装饼干进行卫生达标检验,你准备怎样做?2019/3/15简单随机抽样的概念: 一般地,设一个总体含有N个个体,从中逐个不放回地抽取n个个体作为样本( n?N),如果每次抽取时总体内的各个个体被抽到的机会相等,就把这样的抽样方法叫做简单随机抽样(simple random sampling)。
2019/3/15“简单随机抽样”概念的理解:(1)适用于被抽取样本的总体的个数不多,否则较难“搅拌均匀”,不易操作,产生的样本代表性差的可能性比较大.
(2)从个体数为N的总体中抽取一个容量为n的样本,每个个体被抽到的机会都相等.
(3)具体操作是从总体中逐个抽取,且是不放回的.
(4)简单随机抽样体现了抽样的客观性和公平性,且抽样方法比较简单.2019/3/15抽签法:
例题:高一(17)班有56名学生,现要从中抽取5名学生去参加一个座谈会,每名学生的机会均等,我们可以把56名学生的学号写在小纸片上,揉成小球,放到一个不透明的带子里,充分搅拌后,再从中逐个抽取5个号签,从而抽出5名参加座谈会的学生.2019/3/15抽签法: 一般地,抽签法就是把总体中的N个体编号,把号码写在号签上,将号签放在一个容器里,搅拌均匀后,每次从中抽取一个号签,连续抽取n次,就得到一个容量为n的样本。2019/3/15 编号制签 搅拌均匀逐个不放回抽取n次抽签法步骤:
2.2 用样本估计总体
2.3 变量间的相关关系2019/3/15 我国是世界上第13个贫水国, 人均淡水占有量排列世界第109位! 2019/3/15 章引:
我们生活在一个数字化的时代,时刻都在与数据打交道,例如,产品的合格率,农作物的产量,商品的销售量,当地的气温,自然资源,就业状况,电视台的收视率,你知道这些数据是怎么来的吗?实际上它们是通过调查获得的.怎样调查呢?是对考察对象进行全面调查吗?例如,为了了解计算器的使用寿命,我们能将它们一一测试吗?很明显,这不可能,也没必要.实践中,由于所考察的总体中的个体数往往很多,而且许多考察具有破坏性,因此我们通常只考察总体中的一个样本,通过样本来了解总体的情况.进一步从节约费用的角度考虑,在保证样本估计总体达到一定精度的前提下,样本中包含的个体数越少越好.2019/3/15 于是,如何设计抽样方法,使抽取得样本能够真正代表总体,就成为我们要关注的一个关键问题.否则,如果样本的代表性不好,那么对总体的判断就会出现错误.
那么,怎样从总体中抽取样本呢?如何表示样本数据呢?如何从样本数据中提取基本信息(样本分布,样本数字特征等),来推断总体的情况呢?2019/3/15探究: 假设你作为一名食品卫生工作人员,要对食品店内的一批小包装饼干进行卫生达标检验,你准备怎样做?2019/3/15简单随机抽样的概念: 一般地,设一个总体含有N个个体,从中逐个不放回地抽取n个个体作为样本( n?N),如果每次抽取时总体内的各个个体被抽到的机会相等,就把这样的抽样方法叫做简单随机抽样(simple random sampling)。
2019/3/15“简单随机抽样”概念的理解:(1)适用于被抽取样本的总体的个数不多,否则较难“搅拌均匀”,不易操作,产生的样本代表性差的可能性比较大.
(2)从个体数为N的总体中抽取一个容量为n的样本,每个个体被抽到的机会都相等.
(3)具体操作是从总体中逐个抽取,且是不放回的.
(4)简单随机抽样体现了抽样的客观性和公平性,且抽样方法比较简单.2019/3/15抽签法:
例题:高一(17)班有56名学生,现要从中抽取5名学生去参加一个座谈会,每名学生的机会均等,我们可以把56名学生的学号写在小纸片上,揉成小球,放到一个不透明的带子里,充分搅拌后,再从中逐个抽取5个号签,从而抽出5名参加座谈会的学生.2019/3/15抽签法: 一般地,抽签法就是把总体中的N个体编号,把号码写在号签上,将号签放在一个容器里,搅拌均匀后,每次从中抽取一个号签,连续抽取n次,就得到一个容量为n的样本。2019/3/15 编号制签 搅拌均匀逐个不放回抽取n次抽签法步骤:
