类比推理(1)[下学期]
图片预览





文档简介
课件15张PPT。 定义: 这种有某类事物的部分对象具有
某些特征,推出该类事物的全部对象都
具有这些特征的推理,或者由个别事实
概括出一般结论的推理,称为归纳推理
(简称归纳)。特点:1、由部分到整体,由个别到一般的推理.2、归纳推理的结论不一定正确。复习回顾哥德巴赫猜想 哥德巴赫是德国一位中学教师,1742年,哥
德巴赫在教学中发现一个规律:偶数=奇质数+奇质数。即每
个不小于6的偶数都是两个素质数(只能被和它本身整除的数)
之和。如6=3+3,12=5+7等等。1956年,中国的王元证明
了“3 + 4”。1957年,中国的王元先後证明了“3+3”和“2 + 3”。
1966年,中国的陈景润证明了 “1 + 2”。猜想过程:哥德巴赫观察到10=3+7,20=3+17,30=13+17,
… …得出 偶数=奇质数+奇质数。
验证:4不可以,6=3+3,8=3+5,10=5+5,… …1002=
139+863… … 结论:每个不小于6的偶数都是两个素质数(只能被和它本身
整除的数)之和。【合情推理】
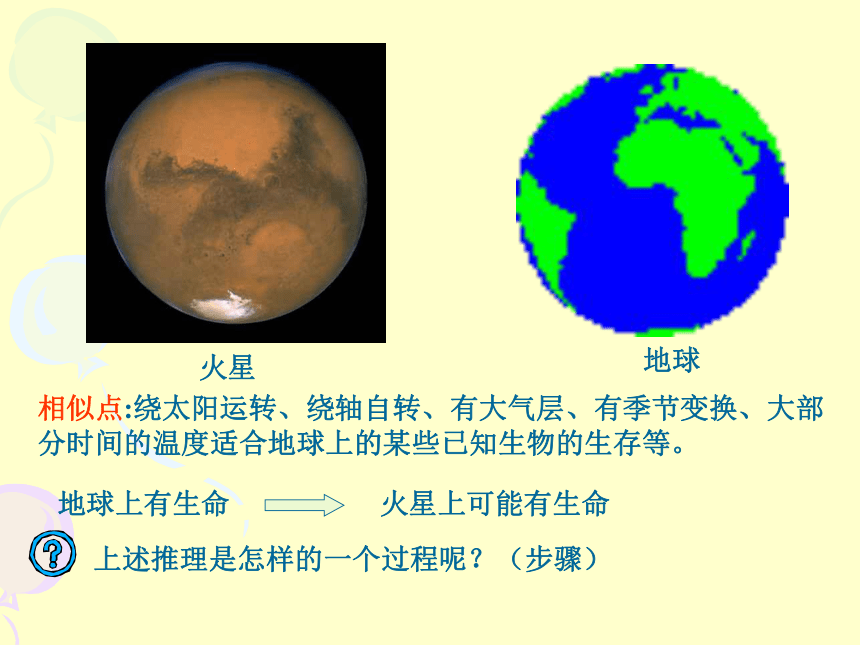
_____类比推理相似点:绕太阳运转、绕轴自转、有大气层、有季节变换、大部
分时间的温度适合地球上的某些已知生物的生存等。地球上有生命火星上可能有生命上述推理是怎样的一个过程呢?(步骤)定义:这种由两类对象具有某些类似的特征和其
中一类对象的某些已知特征,推出另一类对象也
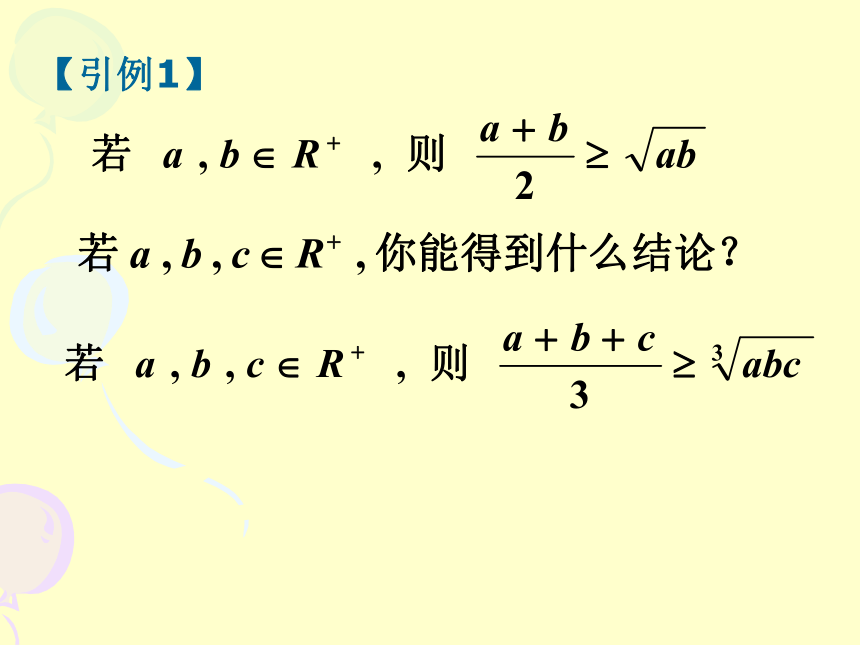
具有这些特征的推理称为类比推理(简称类比)。特点:1、是由特殊到特殊的推理。2、类比推理具有猜测性,不一定可靠。【引例1】【例3】如图,利用类比推测球的有关性质平面向量的坐标运算a =( a1,a2 ), b =( b1,b2 )
a + b =
a – b =
λ a =
a · b =
a∥b
a⊥b
| a | =cosθ=空间向量的坐标运算a =( a1,a2,a3 ), b =( b1,b2,b3 )
a + b =
a – b =
λ a =
a · b =
a∥b
a⊥b
| a | =cos〈a ,b 〉=回顾等差数列的性质1.an = am+ (n-m)d等比数列有哪些性质?2. 等差数列{an}, 若 k + l = p + q 则ak + al = ap + aq1. an = am qn-m2. 等差数列{an}, 若 k + l = p + q 则ak al = ap aq猜一猜: 相应的, 若 a , b 是平面内两个不共线的向量,则
平面内的任意一个向量 p 都可以表示为:
p =x a +y b (平面向量基本定理) 若 a , b ,c是空间三个不共面的向量,则
空间的任意一个向量 p 都可以表示为:
p =x a +y b+z c (空间向量基本定理) 由两类对象具有某些类似特征和其中一
类对象的某些特征,推出另一类对象也具有
这些特征。【类比推理】主要步骤(1)找出两类对象之间的相似
性或一致性;
(2)用一类对象的性质去推测
另一类对象的性质,得出
一个明确的结论。小结:【作业】 《同步导学》
P22-24 1、---、9
某些特征,推出该类事物的全部对象都
具有这些特征的推理,或者由个别事实
概括出一般结论的推理,称为归纳推理
(简称归纳)。特点:1、由部分到整体,由个别到一般的推理.2、归纳推理的结论不一定正确。复习回顾哥德巴赫猜想 哥德巴赫是德国一位中学教师,1742年,哥
德巴赫在教学中发现一个规律:偶数=奇质数+奇质数。即每
个不小于6的偶数都是两个素质数(只能被和它本身整除的数)
之和。如6=3+3,12=5+7等等。1956年,中国的王元证明
了“3 + 4”。1957年,中国的王元先後证明了“3+3”和“2 + 3”。
1966年,中国的陈景润证明了 “1 + 2”。猜想过程:哥德巴赫观察到10=3+7,20=3+17,30=13+17,
… …得出 偶数=奇质数+奇质数。
验证:4不可以,6=3+3,8=3+5,10=5+5,… …1002=
139+863… … 结论:每个不小于6的偶数都是两个素质数(只能被和它本身
整除的数)之和。【合情推理】
_____类比推理相似点:绕太阳运转、绕轴自转、有大气层、有季节变换、大部
分时间的温度适合地球上的某些已知生物的生存等。地球上有生命火星上可能有生命上述推理是怎样的一个过程呢?(步骤)定义:这种由两类对象具有某些类似的特征和其
中一类对象的某些已知特征,推出另一类对象也
具有这些特征的推理称为类比推理(简称类比)。特点:1、是由特殊到特殊的推理。2、类比推理具有猜测性,不一定可靠。【引例1】【例3】如图,利用类比推测球的有关性质平面向量的坐标运算a =( a1,a2 ), b =( b1,b2 )
a + b =
a – b =
λ a =
a · b =
a∥b
a⊥b
| a | =cosθ=空间向量的坐标运算a =( a1,a2,a3 ), b =( b1,b2,b3 )
a + b =
a – b =
λ a =
a · b =
a∥b
a⊥b
| a | =cos〈a ,b 〉=回顾等差数列的性质1.an = am+ (n-m)d等比数列有哪些性质?2. 等差数列{an}, 若 k + l = p + q 则ak + al = ap + aq1. an = am qn-m2. 等差数列{an}, 若 k + l = p + q 则ak al = ap aq猜一猜: 相应的, 若 a , b 是平面内两个不共线的向量,则
平面内的任意一个向量 p 都可以表示为:
p =x a +y b (平面向量基本定理) 若 a , b ,c是空间三个不共面的向量,则
空间的任意一个向量 p 都可以表示为:
p =x a +y b+z c (空间向量基本定理) 由两类对象具有某些类似特征和其中一
类对象的某些特征,推出另一类对象也具有
这些特征。【类比推理】主要步骤(1)找出两类对象之间的相似
性或一致性;
(2)用一类对象的性质去推测
另一类对象的性质,得出
一个明确的结论。小结:【作业】 《同步导学》
P22-24 1、---、9
