【备考2023】广西柳州市中考数学模拟试卷1(含解析)
文档属性
| 名称 | 【备考2023】广西柳州市中考数学模拟试卷1(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-10 10:42:58 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
【备考2023】广西柳州市中考数学模拟试卷1
姓名:__________班级:__________考号:__________总分__________
一、选择题(本大题共12小题,每小题3分,满分36分.在每个小题给出的四个选项中,只有一项是正确的,每小题选对得3分,选错、不选或多选均得0分.)
1.据有关资料显示,全球的森林覆盖面积正以每年15000000公顷的速度沙漠化,每年森林的沙漠化面积用科学记数法表示成( ) 公顷
A. B. C. D.
2.下列标志图中,既是轴对称图形,又是中心对称图形的是 ( )
A. B. C. D.
3.下边的立体图形是由哪个平面图形绕轴旋转一周得到的( )
A. B. C. D.
4.下列调查中,最适合用全面调查(普查)的是( )
A.了解某品牌电脑的使用寿命 B.了解全国中小学生的视力情况
C.调查河南卫视的收视率 D.检测我国研的神舟十三号飞船的零部件的质量
5.数轴上A、B、C、D四个点的位置如图所示,这四个点中,表示2的相反数的点是( )
A.点 A B.点B C.点C D.点D
6.如图,则下列各式中,错误的是( )
A. B. C. D.
7.如图,小红将三角形纸片沿虚线剪去一个角,发现剩下的四边形纸片的周长小于原三角形纸片的周长,下列语句能正确解释这一现象的是( )
A.四边形周长小于三角形周长 B.两点确定一条直线
C.折线比线段长 D.两点之间,线段最短
8.我校是教育部的全国青少年校园足球“满天星”训练基地,旨在“踢出快乐,拼出精彩”,如图,校园足球图片正中的黑色正五边形的内角和是( )
A. B. C. D.
9.将用提公因式法分解因式,应提出的公因式是( )
A. B. C. D.
10.如果圆锥的高为3cm,母线长为5cm,则圆锥的全面积是( )cm2.
A. B. C. D.36π
11.如图所示,已知棋子“车”的坐标为(,),棋子“马”的坐标为(,),则棋子“炮”的坐标为( )
A.(,) B.(,)
C.(,) D.(,)
12.如图,P是函数图象上的点,则的值是( )
A. B. C. D.
二、填空题(本大题典6小题,每小题3分,满分18分.请将答案直接写在答题卡中相应的横线上,在草稿纸、试卷上答题无效)
13.某仓库运进面粉7.5吨记作+7.5吨,那么运出3.8吨应记作_______________.
14.已知一组数据 ,,,4,,,它的平均数是 ,这组数据的众数是________________.
15.(1)_________.(2)__________.
16.如图,在中,,则的度数是___________.
17.正切也经常用来描述山坡的________.坡面与水平面的夹角称为________,坡面的铅直高度与水平宽度的比称为坡度(或坡比),即坡度等于________.
18.如图,正方形ABCD的对角线AC,BD交于点O,以正方形的边长BC为斜边在正方形外作,,若,,则的面积是______.
三、解答题(本大题共8小题,满分66分.解答时应写出必要的文宇说明、演算步骤或推理过程.请将解答写在答题卡中相应的区域内,画图或作辅助线时使用铅笔画出,确定后必须使用黑色字迹的签字笔描黑.在草稿纸、试卷上答题无效.)
19.计算题
(1)3×()+7×() (2)2020()
20.解下列方程(组)
(1) (2)
21.太原武宿国际机场简称“太原机场”,是山西省开通的首条定期国际客运航线.游客从太原某景区乘车到太原机场,有两条路线可供选择,路线一:走迎宾路经太输路全程是25千米,但交通比较拥堵;路线二:走太原环城高速全程是30千米,平均速度是路线一的倍,因此到达太原机场的时间比走路线一少用7分钟,求走路线一到达太原机场需要多长时间.
22.表一:参展的车辆情况.“双碳”背景下,新能源和低碳技术的价值链将成为重中之重,新能源汽车在主流的大众消费群体中越来越受欢迎.某市会展中心正在举行一场新能源汽车的车展活动,此次车展共有三十几种不同品牌的新能源汽车参展,根据不同续航里程可以将这些车分成六类,参展的每一类车辆数如表一:
续航里程x(单位:公里) x≤400 400800
数量(单位:辆) 40 120 132 95 68 45
表二:甲、乙两款车型的三项性能表.
续航里程(单位:公里) 百公里加速(单位:s) 智能化水平
甲车 700 2.70 优秀
乙车 650 1.69 良好
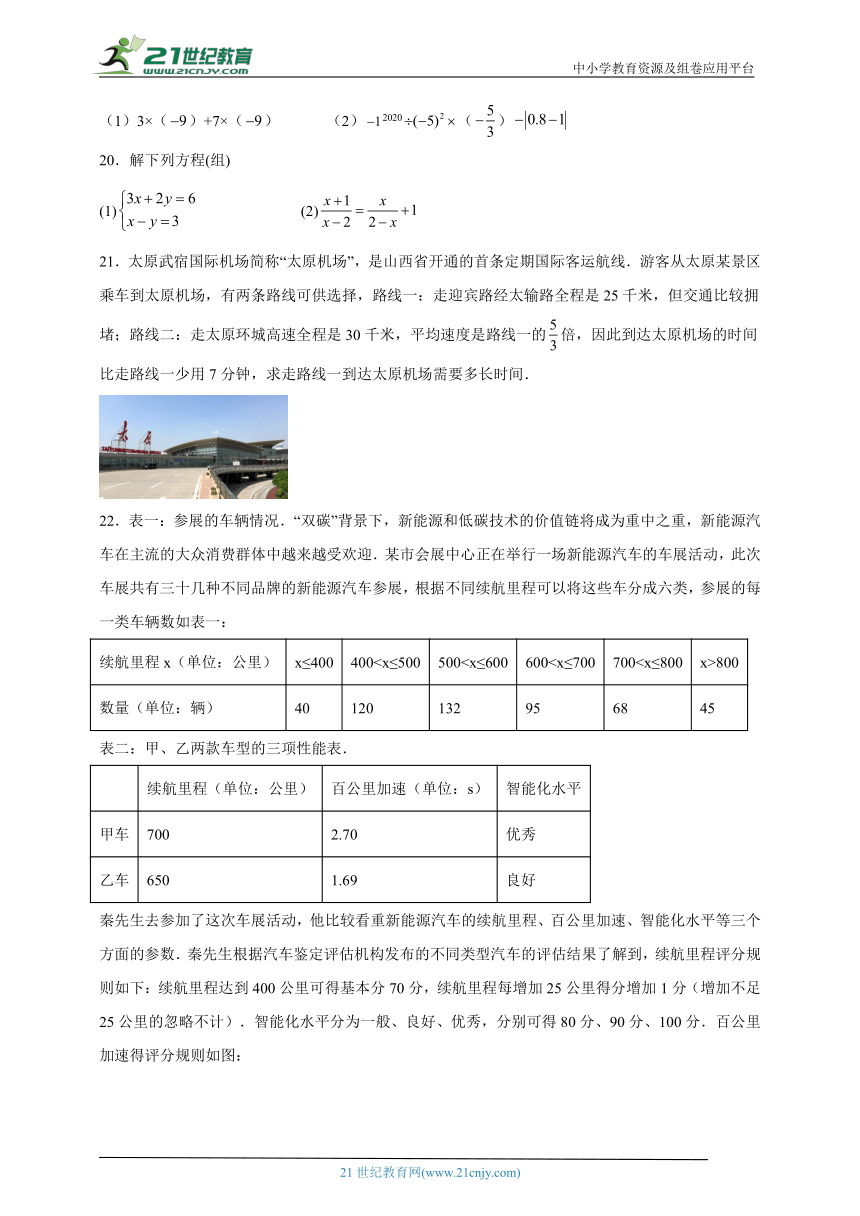
秦先生去参加了这次车展活动,他比较看重新能源汽车的续航里程、百公里加速、智能化水平等三个方面的参数.秦先生根据汽车鉴定评估机构发布的不同类型汽车的评估结果了解到,续航里程评分规则如下:续航里程达到400公里可得基本分70分,续航里程每增加25公里得分增加1分(增加不足25公里的忽略不计).智能化水平分为一般、良好、优秀,分别可得80分、90分、100分.百公里加速得评分规则如图:
(1)秦先生随机选择了一辆车了解车辆信息,记事件A为:选择的是续航里程超过500公里的车辆.求事件A的概率;
(2)新能源汽车的续航里程、百公里加速、智能化水平等三个方面的参数,在秦先生心目中的重要程度分别占,秦先生看中了售价一样的甲、乙两款车,这两款车的三项性能如表二.根据所学的统计与概率的知识,你认为秦先生应选择哪一款汽车比较合适?请说明理由.
23.如图,中,,点在边上,于,点在边上,交于点.
(1)如图1,当,平分时,求的度数;(不用写出每一步的推理原因)
(2)当,时,直接写出的度数.
24.某鲜花销售公司每月付给销售人员的工资有两种方案.
方案一:没有底薪,只付销售提成;
方案二:底薪加销售提成.
如图中的射线,射线分别表示该鲜花销售公司每月按方案一、方案二付给销售人员的工资(单位:元)和(单位:元)与其当月鲜花销售量x(单位:千克)()的函数关系.
(1)直接写出方案二中的底薪是多少元;
(2)求与x的函数解析式;
(3)若该公司某销售人员今年3月份的鲜花销售量没有超过200千克,但其3月份的工资超过5000元.请你判断这个公司采用了哪种方案给这名销售人员付的3月份工资,并说明你的理由.
25.如图,⊙过的顶点、,交于,连接、、,.
(1)证明:为⊙的切线;
(2)平分交于,且分别交、⊙于、.已知,,求的值.
26.如图,在平面直角坐标系中,抛物线与轴交于,两点,与轴交于点,点是该抛物线的顶点.
(1)求抛物线的表达式;
(2)请在轴上找一点,使的周长最小,求出点的坐标;
(3)试探究:在抛物线上是否存在点,使以点为顶点,为直角边的三角形是直角三角形?若存在,请直接写出符合条件的点的坐标;若不存在,请说明理由
参考答案:
1.【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.
解:15 000 000=1.5×107.
故选C.
【点评】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.
2.【分析】根据轴对称图形和中心对称图形的定义进行逐一判断即可.
解:A.不是轴对称图形,是中心对称图形,故A错误;
B.既是轴对称图形,又是中心对称图形,故B正确;
C.是轴对称图形,不是中心对称图形,故C错误;
D.不是轴对称图形,也不是中心对称图形,故D错误.
故选:B.
【点评】本题主要考查了中心对称图形和轴对称图形的定义,如果一个平面图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形;中心对称图形的定义:把一个图形绕着某一个点旋转,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形,这个点就是它的对称中心.
3.【分析】根据面动成体逐项判断即得答案.
解:A、直角梯形绕轴旋转一周得到圆台,故本选项符合题意;
B、半圆绕轴旋转一周得到球,故本选项不符合题意;
C、长方形绕轴旋转一周得到圆柱,故本选项不符合题意;
D、直角三角形绕轴旋转一周得到圆锥,故本选项不符合题意.
故选:A.
【点评】本题考查了点、线、面、体的相关知识,属于基本题型,熟练掌握面动成体是解题关键.
4.【分析】根据抽样调查和全面调查的特点进行逐一判断即可.
解:A、了解某品牌电脑的使用寿命,适合抽样调查;
B、了解全国中小学生的视力情况,适合抽样调查;
C、调查河南卫视的收视率,适合抽样调查;
D、检测我国研的神舟十三号飞船的零部件的质量,适合全面调查.
故选D.
【点评】本题考查了抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大时,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.
5.【分析】根据相反数的定义直接求得结果.
解:数轴上表示2的相反数的点是-2,即A点.
故选:A.
【点评】本题主要考查了数轴及相反数的性质,只有符号不同的两个数互为相反数,0的相反数是0.
6.【分析】根据平行线的性质逐个判断即可.
解:A.∵,
∴,故正确,不符合题意;
B.∵,
∴,故正确,不符合题意;
C.∵,
∴,又,
∴,故错误,符合题意;
D.∵,
∴,故正确,不符合题意;
故选:C.
【点评】本题考查了平行线的性质,能灵活运用平行线的性质进行推理是解此题的关键.
7.【分析】根据两点之间,线段最短进行解答.
解:将三角形纸板沿虚线剪去一部分,我们发现剩下的四边形的周长小于原三角形的周长,正确解释这一现象的数学知识是:两点之间,线段最短.
故选:D.
【点评】本题主要考查了线段的性质,关键是掌握两点之间,线段最短的知识点.
8.【分析】根据多边形内角和公式(n-2)×180°即可求出结果.
解:黑色正五边形的内角和为:(5-2)×180°=540°,
故选C.
【点评】本题考查了多边形的内角和公式,解题关键是牢记多边形的内角和公式.
9.【分析】根据确定公因式的方法进行判断即可.
解:将用提公因式法分解因式,应提出的公因式是,
故选:C.
【点评】本题考查了用提取公因式进行因式分解,解题关键是明确公因式的确定方法.
10.【分析】利用勾股定理易得圆锥的底面半径,那么圆锥的侧面积=底面周长×母线长÷2,再将底面积与侧面积取和即可.
解:圆锥的高为3cm,母线长为5cm,
由勾股定理得,底面半径=4cm,
底面周长=cm,
侧面展开图的面积=×8π×5=20π(cm2).
底面积=(cm2)
所以圆锥的全面积为:(cm2)
故选D.
【点评】本题利用了勾股定理,圆的周长公式和扇形面积公式求解.
11.【分析】先根据棋子“车”的坐标画出直角坐标系,然后写出棋子“炮”的坐标.
解:如图,
棋子“炮”的坐标为(3, 2).
故选:C.
【点评】本题考查了坐标确定位置:平面坐标系中的点与有序实数对一一对应;记住平面内特殊位置的点的坐标特征.
12.【分析】代入,可求出y值,由此可得出点P的坐标可以是,过点P作轴于点Q,在中,利用正切的定义,可求出的值.
解:当时,,
∴点P的坐标可以是.
过点P作轴于点Q,则,如图所示.
在中,,
∴.
故选:D.
【点评】本题考查了一次函数图象上点的坐标特征以及解直角三角形,牢记“直线上任意一点的坐标都满足函数关系式”是解题的关键.
13.【分析】运进面粉记为正,则运出就记为负,直接得出结论即可.
解:运进面粉7.5吨记作+7.5吨,那么运出3.8吨应记作-3.8吨,
故答案为:-3.8吨.
【点评】本题主要考查正负数的意义,正数与负数表示意义相反的两种量,看清规定哪一个为正,则和它意义相反的就为负.
14.【分析】根据求平均数的方法先求出a,再把这组数列出来找出出现次数最多的数即可.
解:a=4×6-(1+3+4+6+7)=3,
这组数据为:1,3,3,4,6,7,
3出现次数最多,则众数为3.
故答案为:3.
【点评】本题考查众数与平均数,解题关键在于根据平均数公式求出a.
15.【分析】根据二次根式的性质和乘法法则化简即可.
解:(1),
(2),
故答案为:,.
【点评】本题考查了二次根式的性质和乘法法则,解题的关键是掌握运算法则.
16.【分析】根据圆周角定理解答即可.
解:∵所对的圆心角是,所对的圆周角是,
∴,
故答案为:.
【点评】本题考查了圆周角定理,熟记同一个圆中,同弧所对圆心角等于所对圆周角的两倍是解题的关键.
17.【分析】根据坡度和坡角的定义解答.
解:正切也经常用来描述山坡的坡比;坡面与水平面的夹角(α)称为坡角,坡面的铅直高度与水平宽度的比称为坡度i(或坡比),即坡度等于tanα.
故答案为坡比、坡角、tanα.
【点评】本题考查了解直角三角形的应用--坡度坡角,本题要熟悉坡度、坡角的定义.
18.【分析】过点E作EG⊥DC交DC的延长线于点G,作EF⊥BC于点F,过点O作OH⊥DC于点H,由勾股定理求出BC=,利用面积相等的性质求出EF=CG=,由勾股定理求出,由正方形的性质可得出,,最后根据即可求解
解:在中,BE=5,CE=3
由勾股定理得,
过点E作EG⊥DC交DC的延长线于点G,作EF⊥BC于点F,过点O作OH⊥DC于点H,如图,
则四边形EFCG是矩形
∴EG=FC,EF=C
又
∴
∴
∴
∵四边形ABCD是正方形,
∴,
∴
=
=
=10
故答案为10
【点评】本题考查了正方形的性质,全等三角形的判定与性质,等腰直角三角形的判定与性质,勾股定理等知识;熟记各性质并准确识图是解决问题的关键.
19.【分析】(1)利用乘法分配律的逆运算即可求解;
(2)根据有理数的混合运算法则计算即可.
解:(1);
(2)原式
.
【点评】本题考查了有理数的混合运算,解题的关键是灵活掌握乘法分配律.
20.【分析】(1)根据加减消元法即可求解;
(2)先将分母进行变形,再去分母即可求解.
解:(1)
令①+2②得5x=12,解得x=
把x=代入②得y=
∴原方程组的解为
(2)
x+1=-x+x-2
解得x=-3,
把x=-3代入原方程,符合题意,
故x=-3是原方程的解.
【点评】此题主要考查方程的求解,解题的关键是熟知加减消元法及分式方程的求解.
21.【分析】设走路线一到达太原机场需要分钟,用含x的式子表示路线一、二的速度,再根据路线二平均速度是路线一的倍列等式计算即可.
解:设走路线一到达太原机场需要分钟.
根据题意,得.
解得:.
经检验,是原方程的解.
答:走路线一到达太原机场需要25分钟.
【点评】本题主要考查分式方程的应用,根据题意找出等量关系是解决本题的关键,注意分式方程需要验根.
22.【分析】(1)根据概率计算公式进行求解即可;
(2)根据题意,计算甲、乙两车的加权平均数,然后比较即可.
解:(1)由表一可知总共有辆车,续航里程超过500公里的车有辆,
∴,
∴事件A的概率为.
(2)由题意知,甲车的续航里程评分为,百公里加速得评分为90,智能化水平得分为100,
∴甲车的平均分为(分),
乙车的续航里程评分为,百公里加速得评分为100,智能化水平得分为90,
∴乙车的平均分为(分),
∵,
∴秦先生应选择甲款汽车比较合适.
【点评】本题考查了简单的概率计算公式,加权平均数等知识.解题的关键在于从题干中获取正确的信息.
23.【分析】(1)先证出,可得,再根据角平分线的定义可得,然后根据,即可求解;
(2)根据题意可分两种情况:若DE在∠ADG的外部时和若DE在∠ADG的外部时,进行求解即可.
解:(1),
,
,
,
∴ ,
,
,
平分,
,
∴ ,
,
,
;
(2)如图,若DE在∠ADG的外部时,
∵,,
∴∠ADG=,
∵,
∴ ,
∴ ,
∵,
∴;
如图,若DE在∠ADG的外部时,
∵,,
∴∠ADG=,
∵,
∴ ,
∴ ,
∵,
∴;
∴的度数为或.
【点评】本题主要考查了平行线的性质和判定,角平分线的定义,熟练掌握平行线的性质和判定,利用分类讨论思想是解题的关键.
24.【分析】(1)根据函数图像即可判断;
(1)根据图像中l2经过的点,利用待定系数法求解即可;
(3)分别根据方案一和方案二列出不等式组,根据解集情况判断即可.
解:(1)
由函数图像可知,方案二中的底薪是800元;
(2)设的解析式为.
由经过点(0,800),(40,1200),
则解得
∴的解析式为.
(3)可求出的解析式为.
由题意可得,
方案一:即解得.
方案二:即即无解.
∴公司没有采用方案二,
∴公司采用了方案一付给这名销售人员3月份的工资.
【点评】本题考查了一次函数的实际应用,一元一次不等式组的应用,解题的关键是结合图像,求出两种方案对应的解析式.
25.【分析】(1)求出即可证明;
(2)作于,连,由,得,,进而,,,由得,即可求得.
(1)证明:设,则
又∵,
∴,
∴,
∴,
∴为的切线;
(2)解:作于,连,
∵,即
又∵平分
∴,即
∴,即
∵,AB=5,
∴设,则
且,则
∴
且
∴,
则,
∴,
∵在中,,
∴,
∵在与中,且,
∴,
∴,
∴,
∴,
∴
∴的值为.
【点评】本题考查圆的综合,熟练掌握圆的切线判定定理,相似三角形的判定与性质,直角三角形的计算是解决问题的关键.
26.【分析】(1)设抛物线解析式为,展开得到,然后求出的值即可得到抛物线的解析式;
(2)利用二次函数的性质确定点的坐标为,作点关于轴的对称点,连接交轴于,如图1,则,利用两点之间线段最短即可判断此时的值最小,此时的周长最小,然后求出直线的解析式即可得到点的坐标;
(3)过点作的垂线交抛物线于另一点,如图2,先用待定系数法求出直线的解析式,利用两直线垂直一次项系数互为负倒数设直线的解析式为,把点的坐标代入求出的值得到直线的解析式,再解方程组得此时点的坐标,过点作的垂线交抛物线于另一点,利用同样的方法可求出此时点的坐标.
解:(1)设抛物线解析式为,
即,
,
解得,
抛物线解析式为:;
(2),
顶点的坐标为,
作点关于轴的对称点,连接交轴于,如图1,则,
,
,此时的值最小,
而的值不变,
此时的周长最小,
设直线的解析式为,将,代入解析式得:
,
解得,
直线的解析式为,
当时,,
点的坐标为;
(3)存在,
过点作的垂线交抛物线于另一点,如图2,
抛物线与轴交于点,
当时,,
点,
设直线的解析式为:,
把,代入得,
,
解得,
直线的解析式为,
,
设直线解析式为:,
把代入得:,
直线解析式为,
解方程组,
解得或,
则此时点坐标为;
过点作的垂线交抛物线于另一点,
则直线的解析式可设为,
把代入得,解得,
直线的解析式为:,
解方程组,
解得或,
则此时点坐标为,
综上所述,符合条件的点的坐标为:或.
【点评】本题考查了二次函数的综合题:熟练掌握二次函数图象上点的坐标特征和二次函数的性质,会利用待定系数法求函数解析式,理解两直线垂直时一次项系数的关系,通过解方程组求两函数的交点坐标,会运用分类讨论的思想解决数学问题.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
【备考2023】广西柳州市中考数学模拟试卷1
姓名:__________班级:__________考号:__________总分__________
一、选择题(本大题共12小题,每小题3分,满分36分.在每个小题给出的四个选项中,只有一项是正确的,每小题选对得3分,选错、不选或多选均得0分.)
1.据有关资料显示,全球的森林覆盖面积正以每年15000000公顷的速度沙漠化,每年森林的沙漠化面积用科学记数法表示成( ) 公顷
A. B. C. D.
2.下列标志图中,既是轴对称图形,又是中心对称图形的是 ( )
A. B. C. D.
3.下边的立体图形是由哪个平面图形绕轴旋转一周得到的( )
A. B. C. D.
4.下列调查中,最适合用全面调查(普查)的是( )
A.了解某品牌电脑的使用寿命 B.了解全国中小学生的视力情况
C.调查河南卫视的收视率 D.检测我国研的神舟十三号飞船的零部件的质量
5.数轴上A、B、C、D四个点的位置如图所示,这四个点中,表示2的相反数的点是( )
A.点 A B.点B C.点C D.点D
6.如图,则下列各式中,错误的是( )
A. B. C. D.
7.如图,小红将三角形纸片沿虚线剪去一个角,发现剩下的四边形纸片的周长小于原三角形纸片的周长,下列语句能正确解释这一现象的是( )
A.四边形周长小于三角形周长 B.两点确定一条直线
C.折线比线段长 D.两点之间,线段最短
8.我校是教育部的全国青少年校园足球“满天星”训练基地,旨在“踢出快乐,拼出精彩”,如图,校园足球图片正中的黑色正五边形的内角和是( )
A. B. C. D.
9.将用提公因式法分解因式,应提出的公因式是( )
A. B. C. D.
10.如果圆锥的高为3cm,母线长为5cm,则圆锥的全面积是( )cm2.
A. B. C. D.36π
11.如图所示,已知棋子“车”的坐标为(,),棋子“马”的坐标为(,),则棋子“炮”的坐标为( )
A.(,) B.(,)
C.(,) D.(,)
12.如图,P是函数图象上的点,则的值是( )
A. B. C. D.
二、填空题(本大题典6小题,每小题3分,满分18分.请将答案直接写在答题卡中相应的横线上,在草稿纸、试卷上答题无效)
13.某仓库运进面粉7.5吨记作+7.5吨,那么运出3.8吨应记作_______________.
14.已知一组数据 ,,,4,,,它的平均数是 ,这组数据的众数是________________.
15.(1)_________.(2)__________.
16.如图,在中,,则的度数是___________.
17.正切也经常用来描述山坡的________.坡面与水平面的夹角称为________,坡面的铅直高度与水平宽度的比称为坡度(或坡比),即坡度等于________.
18.如图,正方形ABCD的对角线AC,BD交于点O,以正方形的边长BC为斜边在正方形外作,,若,,则的面积是______.
三、解答题(本大题共8小题,满分66分.解答时应写出必要的文宇说明、演算步骤或推理过程.请将解答写在答题卡中相应的区域内,画图或作辅助线时使用铅笔画出,确定后必须使用黑色字迹的签字笔描黑.在草稿纸、试卷上答题无效.)
19.计算题
(1)3×()+7×() (2)2020()
20.解下列方程(组)
(1) (2)
21.太原武宿国际机场简称“太原机场”,是山西省开通的首条定期国际客运航线.游客从太原某景区乘车到太原机场,有两条路线可供选择,路线一:走迎宾路经太输路全程是25千米,但交通比较拥堵;路线二:走太原环城高速全程是30千米,平均速度是路线一的倍,因此到达太原机场的时间比走路线一少用7分钟,求走路线一到达太原机场需要多长时间.
22.表一:参展的车辆情况.“双碳”背景下,新能源和低碳技术的价值链将成为重中之重,新能源汽车在主流的大众消费群体中越来越受欢迎.某市会展中心正在举行一场新能源汽车的车展活动,此次车展共有三十几种不同品牌的新能源汽车参展,根据不同续航里程可以将这些车分成六类,参展的每一类车辆数如表一:
续航里程x(单位:公里) x≤400 400
数量(单位:辆) 40 120 132 95 68 45
表二:甲、乙两款车型的三项性能表.
续航里程(单位:公里) 百公里加速(单位:s) 智能化水平
甲车 700 2.70 优秀
乙车 650 1.69 良好
秦先生去参加了这次车展活动,他比较看重新能源汽车的续航里程、百公里加速、智能化水平等三个方面的参数.秦先生根据汽车鉴定评估机构发布的不同类型汽车的评估结果了解到,续航里程评分规则如下:续航里程达到400公里可得基本分70分,续航里程每增加25公里得分增加1分(增加不足25公里的忽略不计).智能化水平分为一般、良好、优秀,分别可得80分、90分、100分.百公里加速得评分规则如图:
(1)秦先生随机选择了一辆车了解车辆信息,记事件A为:选择的是续航里程超过500公里的车辆.求事件A的概率;
(2)新能源汽车的续航里程、百公里加速、智能化水平等三个方面的参数,在秦先生心目中的重要程度分别占,秦先生看中了售价一样的甲、乙两款车,这两款车的三项性能如表二.根据所学的统计与概率的知识,你认为秦先生应选择哪一款汽车比较合适?请说明理由.
23.如图,中,,点在边上,于,点在边上,交于点.
(1)如图1,当,平分时,求的度数;(不用写出每一步的推理原因)
(2)当,时,直接写出的度数.
24.某鲜花销售公司每月付给销售人员的工资有两种方案.
方案一:没有底薪,只付销售提成;
方案二:底薪加销售提成.
如图中的射线,射线分别表示该鲜花销售公司每月按方案一、方案二付给销售人员的工资(单位:元)和(单位:元)与其当月鲜花销售量x(单位:千克)()的函数关系.
(1)直接写出方案二中的底薪是多少元;
(2)求与x的函数解析式;
(3)若该公司某销售人员今年3月份的鲜花销售量没有超过200千克,但其3月份的工资超过5000元.请你判断这个公司采用了哪种方案给这名销售人员付的3月份工资,并说明你的理由.
25.如图,⊙过的顶点、,交于,连接、、,.
(1)证明:为⊙的切线;
(2)平分交于,且分别交、⊙于、.已知,,求的值.
26.如图,在平面直角坐标系中,抛物线与轴交于,两点,与轴交于点,点是该抛物线的顶点.
(1)求抛物线的表达式;
(2)请在轴上找一点,使的周长最小,求出点的坐标;
(3)试探究:在抛物线上是否存在点,使以点为顶点,为直角边的三角形是直角三角形?若存在,请直接写出符合条件的点的坐标;若不存在,请说明理由
参考答案:
1.【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.
解:15 000 000=1.5×107.
故选C.
【点评】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.
2.【分析】根据轴对称图形和中心对称图形的定义进行逐一判断即可.
解:A.不是轴对称图形,是中心对称图形,故A错误;
B.既是轴对称图形,又是中心对称图形,故B正确;
C.是轴对称图形,不是中心对称图形,故C错误;
D.不是轴对称图形,也不是中心对称图形,故D错误.
故选:B.
【点评】本题主要考查了中心对称图形和轴对称图形的定义,如果一个平面图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形;中心对称图形的定义:把一个图形绕着某一个点旋转,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形,这个点就是它的对称中心.
3.【分析】根据面动成体逐项判断即得答案.
解:A、直角梯形绕轴旋转一周得到圆台,故本选项符合题意;
B、半圆绕轴旋转一周得到球,故本选项不符合题意;
C、长方形绕轴旋转一周得到圆柱,故本选项不符合题意;
D、直角三角形绕轴旋转一周得到圆锥,故本选项不符合题意.
故选:A.
【点评】本题考查了点、线、面、体的相关知识,属于基本题型,熟练掌握面动成体是解题关键.
4.【分析】根据抽样调查和全面调查的特点进行逐一判断即可.
解:A、了解某品牌电脑的使用寿命,适合抽样调查;
B、了解全国中小学生的视力情况,适合抽样调查;
C、调查河南卫视的收视率,适合抽样调查;
D、检测我国研的神舟十三号飞船的零部件的质量,适合全面调查.
故选D.
【点评】本题考查了抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大时,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.
5.【分析】根据相反数的定义直接求得结果.
解:数轴上表示2的相反数的点是-2,即A点.
故选:A.
【点评】本题主要考查了数轴及相反数的性质,只有符号不同的两个数互为相反数,0的相反数是0.
6.【分析】根据平行线的性质逐个判断即可.
解:A.∵,
∴,故正确,不符合题意;
B.∵,
∴,故正确,不符合题意;
C.∵,
∴,又,
∴,故错误,符合题意;
D.∵,
∴,故正确,不符合题意;
故选:C.
【点评】本题考查了平行线的性质,能灵活运用平行线的性质进行推理是解此题的关键.
7.【分析】根据两点之间,线段最短进行解答.
解:将三角形纸板沿虚线剪去一部分,我们发现剩下的四边形的周长小于原三角形的周长,正确解释这一现象的数学知识是:两点之间,线段最短.
故选:D.
【点评】本题主要考查了线段的性质,关键是掌握两点之间,线段最短的知识点.
8.【分析】根据多边形内角和公式(n-2)×180°即可求出结果.
解:黑色正五边形的内角和为:(5-2)×180°=540°,
故选C.
【点评】本题考查了多边形的内角和公式,解题关键是牢记多边形的内角和公式.
9.【分析】根据确定公因式的方法进行判断即可.
解:将用提公因式法分解因式,应提出的公因式是,
故选:C.
【点评】本题考查了用提取公因式进行因式分解,解题关键是明确公因式的确定方法.
10.【分析】利用勾股定理易得圆锥的底面半径,那么圆锥的侧面积=底面周长×母线长÷2,再将底面积与侧面积取和即可.
解:圆锥的高为3cm,母线长为5cm,
由勾股定理得,底面半径=4cm,
底面周长=cm,
侧面展开图的面积=×8π×5=20π(cm2).
底面积=(cm2)
所以圆锥的全面积为:(cm2)
故选D.
【点评】本题利用了勾股定理,圆的周长公式和扇形面积公式求解.
11.【分析】先根据棋子“车”的坐标画出直角坐标系,然后写出棋子“炮”的坐标.
解:如图,
棋子“炮”的坐标为(3, 2).
故选:C.
【点评】本题考查了坐标确定位置:平面坐标系中的点与有序实数对一一对应;记住平面内特殊位置的点的坐标特征.
12.【分析】代入,可求出y值,由此可得出点P的坐标可以是,过点P作轴于点Q,在中,利用正切的定义,可求出的值.
解:当时,,
∴点P的坐标可以是.
过点P作轴于点Q,则,如图所示.
在中,,
∴.
故选:D.
【点评】本题考查了一次函数图象上点的坐标特征以及解直角三角形,牢记“直线上任意一点的坐标都满足函数关系式”是解题的关键.
13.【分析】运进面粉记为正,则运出就记为负,直接得出结论即可.
解:运进面粉7.5吨记作+7.5吨,那么运出3.8吨应记作-3.8吨,
故答案为:-3.8吨.
【点评】本题主要考查正负数的意义,正数与负数表示意义相反的两种量,看清规定哪一个为正,则和它意义相反的就为负.
14.【分析】根据求平均数的方法先求出a,再把这组数列出来找出出现次数最多的数即可.
解:a=4×6-(1+3+4+6+7)=3,
这组数据为:1,3,3,4,6,7,
3出现次数最多,则众数为3.
故答案为:3.
【点评】本题考查众数与平均数,解题关键在于根据平均数公式求出a.
15.【分析】根据二次根式的性质和乘法法则化简即可.
解:(1),
(2),
故答案为:,.
【点评】本题考查了二次根式的性质和乘法法则,解题的关键是掌握运算法则.
16.【分析】根据圆周角定理解答即可.
解:∵所对的圆心角是,所对的圆周角是,
∴,
故答案为:.
【点评】本题考查了圆周角定理,熟记同一个圆中,同弧所对圆心角等于所对圆周角的两倍是解题的关键.
17.【分析】根据坡度和坡角的定义解答.
解:正切也经常用来描述山坡的坡比;坡面与水平面的夹角(α)称为坡角,坡面的铅直高度与水平宽度的比称为坡度i(或坡比),即坡度等于tanα.
故答案为坡比、坡角、tanα.
【点评】本题考查了解直角三角形的应用--坡度坡角,本题要熟悉坡度、坡角的定义.
18.【分析】过点E作EG⊥DC交DC的延长线于点G,作EF⊥BC于点F,过点O作OH⊥DC于点H,由勾股定理求出BC=,利用面积相等的性质求出EF=CG=,由勾股定理求出,由正方形的性质可得出,,最后根据即可求解
解:在中,BE=5,CE=3
由勾股定理得,
过点E作EG⊥DC交DC的延长线于点G,作EF⊥BC于点F,过点O作OH⊥DC于点H,如图,
则四边形EFCG是矩形
∴EG=FC,EF=C
又
∴
∴
∴
∵四边形ABCD是正方形,
∴,
∴
=
=
=10
故答案为10
【点评】本题考查了正方形的性质,全等三角形的判定与性质,等腰直角三角形的判定与性质,勾股定理等知识;熟记各性质并准确识图是解决问题的关键.
19.【分析】(1)利用乘法分配律的逆运算即可求解;
(2)根据有理数的混合运算法则计算即可.
解:(1);
(2)原式
.
【点评】本题考查了有理数的混合运算,解题的关键是灵活掌握乘法分配律.
20.【分析】(1)根据加减消元法即可求解;
(2)先将分母进行变形,再去分母即可求解.
解:(1)
令①+2②得5x=12,解得x=
把x=代入②得y=
∴原方程组的解为
(2)
x+1=-x+x-2
解得x=-3,
把x=-3代入原方程,符合题意,
故x=-3是原方程的解.
【点评】此题主要考查方程的求解,解题的关键是熟知加减消元法及分式方程的求解.
21.【分析】设走路线一到达太原机场需要分钟,用含x的式子表示路线一、二的速度,再根据路线二平均速度是路线一的倍列等式计算即可.
解:设走路线一到达太原机场需要分钟.
根据题意,得.
解得:.
经检验,是原方程的解.
答:走路线一到达太原机场需要25分钟.
【点评】本题主要考查分式方程的应用,根据题意找出等量关系是解决本题的关键,注意分式方程需要验根.
22.【分析】(1)根据概率计算公式进行求解即可;
(2)根据题意,计算甲、乙两车的加权平均数,然后比较即可.
解:(1)由表一可知总共有辆车,续航里程超过500公里的车有辆,
∴,
∴事件A的概率为.
(2)由题意知,甲车的续航里程评分为,百公里加速得评分为90,智能化水平得分为100,
∴甲车的平均分为(分),
乙车的续航里程评分为,百公里加速得评分为100,智能化水平得分为90,
∴乙车的平均分为(分),
∵,
∴秦先生应选择甲款汽车比较合适.
【点评】本题考查了简单的概率计算公式,加权平均数等知识.解题的关键在于从题干中获取正确的信息.
23.【分析】(1)先证出,可得,再根据角平分线的定义可得,然后根据,即可求解;
(2)根据题意可分两种情况:若DE在∠ADG的外部时和若DE在∠ADG的外部时,进行求解即可.
解:(1),
,
,
,
∴ ,
,
,
平分,
,
∴ ,
,
,
;
(2)如图,若DE在∠ADG的外部时,
∵,,
∴∠ADG=,
∵,
∴ ,
∴ ,
∵,
∴;
如图,若DE在∠ADG的外部时,
∵,,
∴∠ADG=,
∵,
∴ ,
∴ ,
∵,
∴;
∴的度数为或.
【点评】本题主要考查了平行线的性质和判定,角平分线的定义,熟练掌握平行线的性质和判定,利用分类讨论思想是解题的关键.
24.【分析】(1)根据函数图像即可判断;
(1)根据图像中l2经过的点,利用待定系数法求解即可;
(3)分别根据方案一和方案二列出不等式组,根据解集情况判断即可.
解:(1)
由函数图像可知,方案二中的底薪是800元;
(2)设的解析式为.
由经过点(0,800),(40,1200),
则解得
∴的解析式为.
(3)可求出的解析式为.
由题意可得,
方案一:即解得.
方案二:即即无解.
∴公司没有采用方案二,
∴公司采用了方案一付给这名销售人员3月份的工资.
【点评】本题考查了一次函数的实际应用,一元一次不等式组的应用,解题的关键是结合图像,求出两种方案对应的解析式.
25.【分析】(1)求出即可证明;
(2)作于,连,由,得,,进而,,,由得,即可求得.
(1)证明:设,则
又∵,
∴,
∴,
∴,
∴为的切线;
(2)解:作于,连,
∵,即
又∵平分
∴,即
∴,即
∵,AB=5,
∴设,则
且,则
∴
且
∴,
则,
∴,
∵在中,,
∴,
∵在与中,且,
∴,
∴,
∴,
∴,
∴
∴的值为.
【点评】本题考查圆的综合,熟练掌握圆的切线判定定理,相似三角形的判定与性质,直角三角形的计算是解决问题的关键.
26.【分析】(1)设抛物线解析式为,展开得到,然后求出的值即可得到抛物线的解析式;
(2)利用二次函数的性质确定点的坐标为,作点关于轴的对称点,连接交轴于,如图1,则,利用两点之间线段最短即可判断此时的值最小,此时的周长最小,然后求出直线的解析式即可得到点的坐标;
(3)过点作的垂线交抛物线于另一点,如图2,先用待定系数法求出直线的解析式,利用两直线垂直一次项系数互为负倒数设直线的解析式为,把点的坐标代入求出的值得到直线的解析式,再解方程组得此时点的坐标,过点作的垂线交抛物线于另一点,利用同样的方法可求出此时点的坐标.
解:(1)设抛物线解析式为,
即,
,
解得,
抛物线解析式为:;
(2),
顶点的坐标为,
作点关于轴的对称点,连接交轴于,如图1,则,
,
,此时的值最小,
而的值不变,
此时的周长最小,
设直线的解析式为,将,代入解析式得:
,
解得,
直线的解析式为,
当时,,
点的坐标为;
(3)存在,
过点作的垂线交抛物线于另一点,如图2,
抛物线与轴交于点,
当时,,
点,
设直线的解析式为:,
把,代入得,
,
解得,
直线的解析式为,
,
设直线解析式为:,
把代入得:,
直线解析式为,
解方程组,
解得或,
则此时点坐标为;
过点作的垂线交抛物线于另一点,
则直线的解析式可设为,
把代入得,解得,
直线的解析式为:,
解方程组,
解得或,
则此时点坐标为,
综上所述,符合条件的点的坐标为:或.
【点评】本题考查了二次函数的综合题:熟练掌握二次函数图象上点的坐标特征和二次函数的性质,会利用待定系数法求函数解析式,理解两直线垂直时一次项系数的关系,通过解方程组求两函数的交点坐标,会运用分类讨论的思想解决数学问题.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
