18.2.3 正方形的性质和判定 同步训练(含答案)
文档属性
| 名称 | 18.2.3 正方形的性质和判定 同步训练(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-10 17:42:45 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
18.2.3正方形的性质和判定训练
一、选择题
1.下列说法中,是正方形具有而矩形不具有的性质是( )
A.两组对边分别平行 B.对角线互相垂直 C.四个角都为直角 D.对角线互相平分
2.下列说法中正确的是( )
A.矩形的对角线平分每组对角 B.菱形的对角线相等且互相垂直
C.有一组邻边相等的矩形是正方形 D.对角线互相垂直的四边形是菱形
3.已知四边形ABCD是平行四边形,AC,BD相交于点O,下列结论错误的是( )
A.OA=OC,OB=OD B.当AB=CD时,四边形ABCD是菱形
C.当∠ABC=90°时,四边形ABCD是矩形
D.当AC=BD且AC⊥BD时,四边形ABCD是正方形
4.边长为4的正方形ABCD中,P是边AD上的动点,PE⊥AC于点E,PF⊥BD于点F,则PE+PF的值为
A.2 B.4 C.2 D.6
5.如图,在正方形ABCD中,点E在对角线AC上,EF⊥AB于点F,EG⊥BC于点G,连接DE,若AB=10,AE=3,则ED的长度为( )
A.7 B.2 C. D.
6.如图,在正方形ABCD内作等边三角形DCE,则∠EAC=( )
A.35° B.28° C.30° D.45°
7.如图,在正方形ABCD的外侧,作等边△ABE,则∠BED为( )
A.15° B.35° C.45° D.55°
8.如图,在正方形ABCD中,点E,F分别在BC,CD上,BE=CF,则图中与∠AEB相等的角的个数是( )
A.1 B.2 C.3 D.4
9.如图,在平面直角坐标系中,正方形OABC的顶点O,B的坐标分别是(0,0);(4,0),则顶点C的坐标是( )
A.(2,2) B.(2,﹣2) C.(﹣2,2) D.( 2,﹣2)
10.如图,已知在正方形ABCD中,AB=10厘米,点E在边AB上,且AE=4厘米,如果点P在线段BC上以2厘米/秒的速度由B点向C点运动,同时,点Q在线段CD上由C点向D点运动,设运动时间为t秒.当△BPE与△CQP全等时,t的值为( )
A.2 B.2或1.5 C.2.5 D.2.5或2
二、填空题
11.已知正方形ABCD的周长为24,则AB=___,AC=____,正方形ABCD的面积为_____
12.如图,四边形ABCD是正方形,以CD为边向外作等边△CDE,则∠DAE=_____.
13.如图,在正方形ABCD中,E是对角线BD上一点,AE的延长线交CD于点F,连接CE.若∠BA=56°,则∠CEF= °.
14.如图,在边长为4的正方形ABCD中,点M为对角线BD上一动点,ME⊥BC于E,MF⊥CD于F,则EF的最小值为 .
三、解答题
15.已知:如图,在正方形ABCD中,对角线AC,BD相交于点O,点E,F分别是边BC,CD上的点,且∠EOF=90°.
求证:CE=DF.
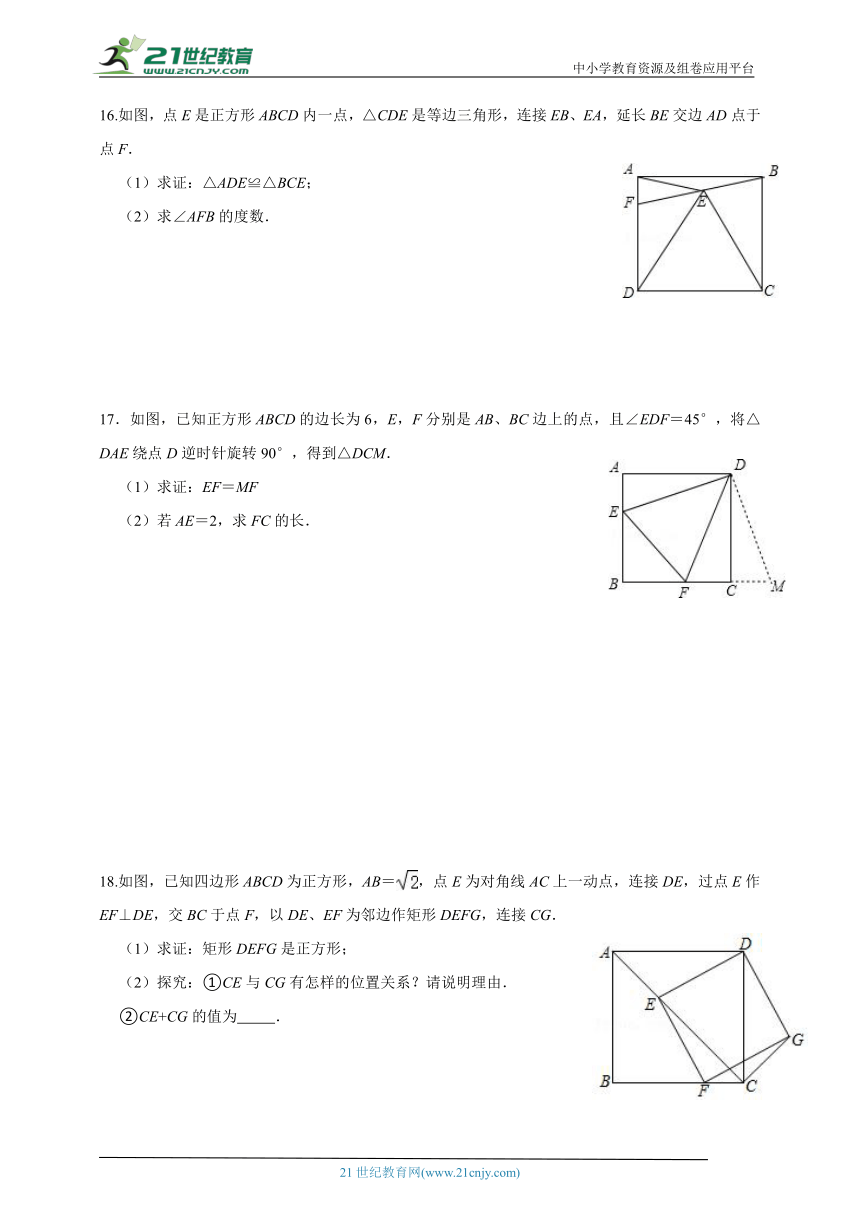
16.如图,点E是正方形ABCD内一点,△CDE是等边三角形,连接EB、EA,延长BE交边AD点于点F.
(1)求证:△ADE≌△BCE;
(2)求∠AFB的度数.
17.如图,已知正方形ABCD的边长为6,E,F分别是AB、BC边上的点,且∠EDF=45°,将△DAE绕点D逆时针旋转90°,得到△DCM.
(1)求证:EF=MF
(2)若AE=2,求FC的长.
18.如图,已知四边形ABCD为正方形,AB=,点E为对角线AC上一动点,连接DE,过点E作EF⊥DE,交BC于点F,以DE、EF为邻边作矩形DEFG,连接CG.
(1)求证:矩形DEFG是正方形;
(2)探究:①CE与CG有怎样的位置关系?请说明理由.
②CE+CG的值为 .
19.如图,点E是正方形ABCD对角线AC上一点,EF⊥AB,EG⊥BC,垂足分别为F,G,若正方形ABCD的周长是40cm.
(1)求证:四边形BFEG是矩形;
(2)求四边形EFBG的周长;
(3)当AF的长为多少时,四边形BFEG是正方形?
20.如图,四边形ABCD是正方形,点E,K分别在BC,AB上,点G在BA的延长线上,且CE=BK=AG.
(1)求证:①DE=DG;②DE⊥DG
(2)尺规作图:以线段DE,DG为边作出正方形DEFG(要求:只保留作图痕迹,不写作法和证明);
(3)连接(2)中KF,猜想并写出四边形CEFK是怎样的特殊四边形,并证明你的猜想;
参考答案
一、选择题
1.B
2.C
3.B
4.A
5.C
6.C
7.C
8.C
9.B
10.D
二、填空题
11.AB=6;AC=6;36
12.15°
13.22°
14.2
解答题
15.
16.
17.
18.
19.
20.
5题 6题 7题 8题
9题 10题 12题 13题
14题
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
18.2.3正方形的性质和判定训练
一、选择题
1.下列说法中,是正方形具有而矩形不具有的性质是( )
A.两组对边分别平行 B.对角线互相垂直 C.四个角都为直角 D.对角线互相平分
2.下列说法中正确的是( )
A.矩形的对角线平分每组对角 B.菱形的对角线相等且互相垂直
C.有一组邻边相等的矩形是正方形 D.对角线互相垂直的四边形是菱形
3.已知四边形ABCD是平行四边形,AC,BD相交于点O,下列结论错误的是( )
A.OA=OC,OB=OD B.当AB=CD时,四边形ABCD是菱形
C.当∠ABC=90°时,四边形ABCD是矩形
D.当AC=BD且AC⊥BD时,四边形ABCD是正方形
4.边长为4的正方形ABCD中,P是边AD上的动点,PE⊥AC于点E,PF⊥BD于点F,则PE+PF的值为
A.2 B.4 C.2 D.6
5.如图,在正方形ABCD中,点E在对角线AC上,EF⊥AB于点F,EG⊥BC于点G,连接DE,若AB=10,AE=3,则ED的长度为( )
A.7 B.2 C. D.
6.如图,在正方形ABCD内作等边三角形DCE,则∠EAC=( )
A.35° B.28° C.30° D.45°
7.如图,在正方形ABCD的外侧,作等边△ABE,则∠BED为( )
A.15° B.35° C.45° D.55°
8.如图,在正方形ABCD中,点E,F分别在BC,CD上,BE=CF,则图中与∠AEB相等的角的个数是( )
A.1 B.2 C.3 D.4
9.如图,在平面直角坐标系中,正方形OABC的顶点O,B的坐标分别是(0,0);(4,0),则顶点C的坐标是( )
A.(2,2) B.(2,﹣2) C.(﹣2,2) D.( 2,﹣2)
10.如图,已知在正方形ABCD中,AB=10厘米,点E在边AB上,且AE=4厘米,如果点P在线段BC上以2厘米/秒的速度由B点向C点运动,同时,点Q在线段CD上由C点向D点运动,设运动时间为t秒.当△BPE与△CQP全等时,t的值为( )
A.2 B.2或1.5 C.2.5 D.2.5或2
二、填空题
11.已知正方形ABCD的周长为24,则AB=___,AC=____,正方形ABCD的面积为_____
12.如图,四边形ABCD是正方形,以CD为边向外作等边△CDE,则∠DAE=_____.
13.如图,在正方形ABCD中,E是对角线BD上一点,AE的延长线交CD于点F,连接CE.若∠BA=56°,则∠CEF= °.
14.如图,在边长为4的正方形ABCD中,点M为对角线BD上一动点,ME⊥BC于E,MF⊥CD于F,则EF的最小值为 .
三、解答题
15.已知:如图,在正方形ABCD中,对角线AC,BD相交于点O,点E,F分别是边BC,CD上的点,且∠EOF=90°.
求证:CE=DF.
16.如图,点E是正方形ABCD内一点,△CDE是等边三角形,连接EB、EA,延长BE交边AD点于点F.
(1)求证:△ADE≌△BCE;
(2)求∠AFB的度数.
17.如图,已知正方形ABCD的边长为6,E,F分别是AB、BC边上的点,且∠EDF=45°,将△DAE绕点D逆时针旋转90°,得到△DCM.
(1)求证:EF=MF
(2)若AE=2,求FC的长.
18.如图,已知四边形ABCD为正方形,AB=,点E为对角线AC上一动点,连接DE,过点E作EF⊥DE,交BC于点F,以DE、EF为邻边作矩形DEFG,连接CG.
(1)求证:矩形DEFG是正方形;
(2)探究:①CE与CG有怎样的位置关系?请说明理由.
②CE+CG的值为 .
19.如图,点E是正方形ABCD对角线AC上一点,EF⊥AB,EG⊥BC,垂足分别为F,G,若正方形ABCD的周长是40cm.
(1)求证:四边形BFEG是矩形;
(2)求四边形EFBG的周长;
(3)当AF的长为多少时,四边形BFEG是正方形?
20.如图,四边形ABCD是正方形,点E,K分别在BC,AB上,点G在BA的延长线上,且CE=BK=AG.
(1)求证:①DE=DG;②DE⊥DG
(2)尺规作图:以线段DE,DG为边作出正方形DEFG(要求:只保留作图痕迹,不写作法和证明);
(3)连接(2)中KF,猜想并写出四边形CEFK是怎样的特殊四边形,并证明你的猜想;
参考答案
一、选择题
1.B
2.C
3.B
4.A
5.C
6.C
7.C
8.C
9.B
10.D
二、填空题
11.AB=6;AC=6;36
12.15°
13.22°
14.2
解答题
15.
16.
17.
18.
19.
20.
5题 6题 7题 8题
9题 10题 12题 13题
14题
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
