人教版五年级数学下册5.图形的运动(三)同步练习(含答案)
文档属性
| 名称 | 人教版五年级数学下册5.图形的运动(三)同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 538.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-10 14:55:15 | ||
图片预览

文档简介
人教版 五年级数学下册
5.图形的运动(三) 同步练习 (含答案)
一、填空题
1.图形经过( )时针,旋转( )°后,能将右图填满,正好成为长方形。
2.将△ABC绕点A顺时针旋转90°,与点B对应的点我们记作B’与点C对应的点我们记作C'。
如果点A的位置用数对(5,4)表示,B点用数对(8,6)表示,那么点B'用数对表示为( ),那么点C'用数对表示为( )。
3.
(注意:图在格内所画的竖线、横线都是与格子竖线、横线重合的!)
(1)小帆船先向( )平移了( )格,再向( )平移了( )格。
(2)三角形先向( )平移了( )格,再向( )平移了( )格。
4.从9:00到6:00,时针沿逆时针旋转了( )°。
5.可以看做是由一个基本图形按顺时针或逆时针方向连续经过了( )次旋转,且每次旋转( )°得到的。
6.如图,扇子打开时,扇柄的一侧不动,另一侧绕点O( )时针方向旋转了( )°。
7.钟面上,分针绕中心点从3时30分开始按顺时针方向旋转90°后是( )时( )分。
二、选择题
8.如图,三角形M绕点O顺时针旋转90°得到的图形是( )。
A. B. C.
9.从12:00到12:20,分针绕中心点顺时针旋转了( )。
A.20° B.30° C.120°
10.钟面上,如果分针旋转半圈,那么时针旋转( )。
A.15° B.30° C.90°
11.把一个图形逆时针旋转45°后,所得的图形与原图形相比较( )。
A.变大了 B.变小了 C.大小不变
12.下面的图形中,通过旋转可以得到图形A的是( )。
A.①② B.①③ C.②④
13.把长方形绕0点顺时针旋转90°后,得到的图形是( )。
A. B. C.
14.如图,将图形①经过( )可以得到图形②。
A.向右平移2格 B.向上平移2格 C.绕点O顺时针旋转90°
15.如下图,小猴子从点A起绕房子逆时针转一圈,所看到房子的图片排序正确的是( )。
A.①②③④ B.①③②④ C.③②④①
16.将下列图形绕着各自的中心点旋转120°后,不能与原来的图形重合的是( )。
A. B. C.
三、判断题
17.钟面上的分针,从12绕中心轴顺时针旋转90°就到了“3”。( )
18.图中钟面上的时针绕中心点顺时针方向旋转了90°。( )
19.从4时到5时,时针顺时针旋转了30°。( )
20.电风扇的扇叶做平移运动。( )
四、解答题
21.如图,白色部分DEFB是一个正方形,AE长4厘米,EC长8厘米。阴影部分的面积是多少平方厘米?
提示:怎样把两个阴影部分拼到一起呢?
我们可以这样思考:
(1)将三角形ADE绕点E逆时针旋转90°,画出旋转后的图形。这样两个阴影部分就拼到一起了。
(2)因为( ),所以组合后的阴影部分是一个( )三角形。
(3)旋转后的AE长4厘米,EC长8厘米,阴影部分的面积是( )平方厘米。
22.如图,每个方格的边长表示1厘米。
(1)图中的平行四边形沿高分成了两部分,将涂色的三角形向右平移( )厘米,平行四边形就转化成了长方形。
(2)把三角形ABC绕点B顺时针旋转90°,画出旋转后的图形。
(3)画出图中下方图形的另一半,使它成为轴对称图形。
23.操作。
(1)在如图方格图中描出点A(6,6),点B(3,2),点C(6,2),并顺次连接三点。
(2)连接后的图形是( )三角形,它的面积是( )cm。
(3)画出这个三角形绕点C顺时针旋转90后的图形,并标上A1、B1、C1。
试卷第1页,共3页
试卷第1页,共3页
参考答案
1. 顺 180
【分析】观察右图空白部分的图形应为,才能组成长方形,根据旋转的特征,图形经过顺时针旋转180°后,就能形成这样的图形,据此解答。
【详解】根据分析得,图形经过顺时针,旋转180°后,能将右图填满,正好成为长方形。
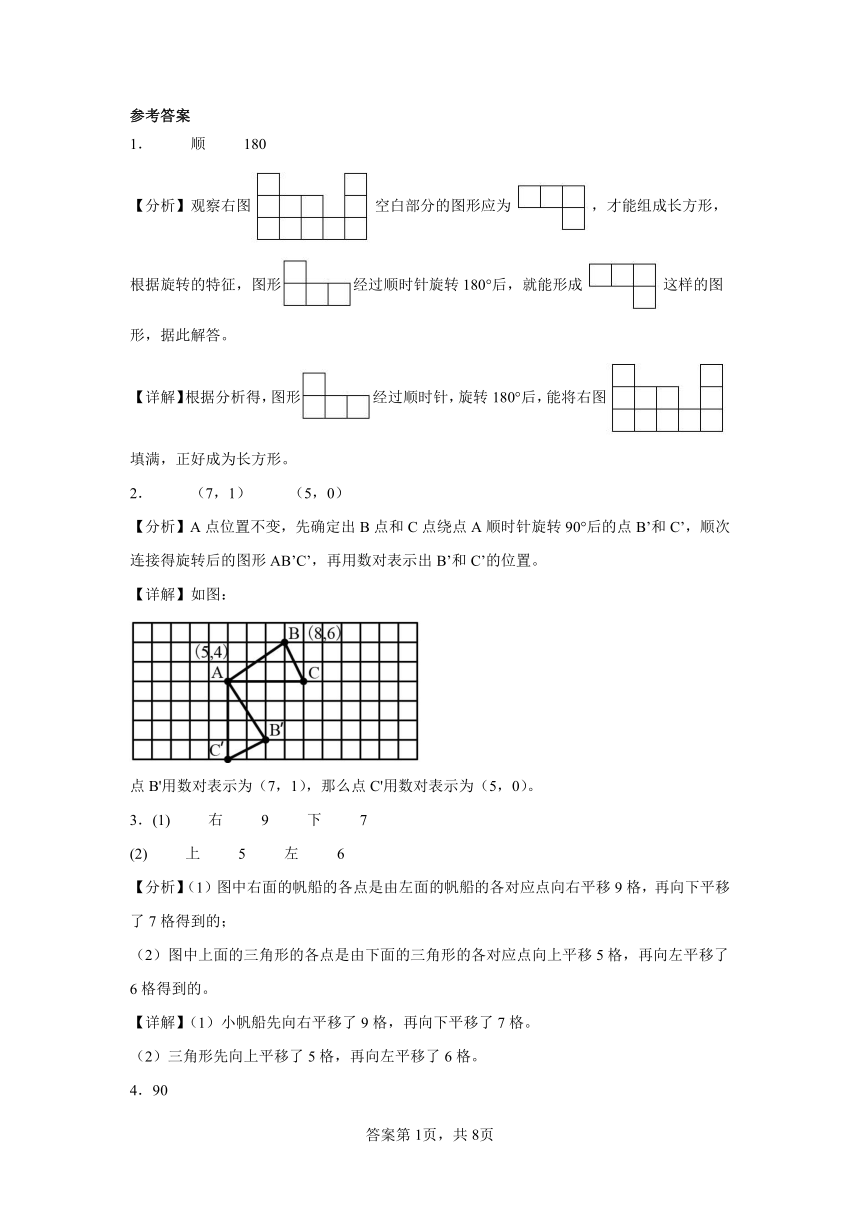
2. (7,1) (5,0)
【分析】A点位置不变,先确定出B点和C点绕点A顺时针旋转90°后的点B’和C’,顺次连接得旋转后的图形AB’C’,再用数对表示出B’和C’的位置。
【详解】如图:
点B'用数对表示为(7,1),那么点C'用数对表示为(5,0)。
3.(1) 右 9 下 7
(2) 上 5 左 6
【分析】(1)图中右面的帆船的各点是由左面的帆船的各对应点向右平移9格,再向下平移了7格得到的;
(2)图中上面的三角形的各点是由下面的三角形的各对应点向上平移5格,再向左平移了6格得到的。
【详解】(1)小帆船先向右平移了9格,再向下平移了7格。
(2)三角形先向上平移了5格,再向左平移了6格。
4.90
【分析】在钟表中共有12个大格,则每个大格有360°÷12=30°,因为9:00到6:00共有3个大格,据此选择即可。
【详解】3×30°=90°
则从9:00到6:00,时针沿逆时针旋转了90°。
5. 3 90
【分析】看图,由一个基本图形,旋转之后变成了四个一模一样的图形,所以是经过了三次旋转。再观察发现,每次的旋转角度是90°。
【详解】可以看做是由一个基本图形按顺时针或逆时针方向连续经过了3次旋转,且每次旋转90°得到的。
6. 顺 90
【分析】根据旋转的特征,扇子打开时,将扇子绕O点顺时针旋转90°,点O位置不变,其余各部分均绕此点按相同方向旋转相同度数,即顺时针旋转90°,据此解答。
【详解】扇子打开时,扇柄的一侧不动,另一侧绕点O顺时针方向旋转了90°。
7. 3 45
【分析】钟面上12个数字,以表芯为旋转点,表针转一圈是360°,被12个数字平均分成12份,每一份也就是两数之间夹角是30°。分针绕中心点从3时30分开始按顺时针方向旋转90°,也就是三大格,经过15分钟,旋转后是3:45。
【详解】钟面上,分针绕中心点从3时30分开始按顺时针方向旋转90°后是3时45分。
8.A
【分析】图形的旋转是图形上的每个点在平面上绕着某个固定点旋转固定角度的位置移动,其中对应点到旋转中心的距离相等,对应线段的长度、对应角的大小相等,且旋转前后图形的大小和形状没有改变,三角形M绕点O顺时针旋转90°,点O的位置不动,三角形M的各部分绕点O按相同的方向旋转相同的度数,据此解答。
【详解】A.三角形M绕点O顺时针旋转90°得到;
B.三角形M绕点O逆时针旋转90°得到;
C.三角形M绕点O顺(逆)时针旋转180°得到;
故答案为:A
9.C
【分析】分针绕一周是60分钟,也就是把钟面的圆平均分成60份,一个圆是360°,平均分成60份,先用除法求出一份是多少度,从12:00到12:20是20分钟,也就是其中的20份。用乘法计算即可求出旋转了多少度。
【详解】360°÷60=6°
6°×20=120°
分针绕中心点顺时针旋转了120°。
故答案为:C
10.A
【分析】时针或分针绕钟面旋转一周是360°,整个钟面被平均分成12大格,一个大格是30°,时针一小时旋转一个大格,分针一小时绕钟面旋转一周,如果分针绕钟面旋转半周,一共是半个小时,则分针旋转半个大格,据此解答。
【详解】360°÷12÷2
=30°÷2
=15°
所以,钟面上,如果分针旋转半圈,那么时针旋转15°。
故答案为:A
11.C
【分析】根据旋转图形的特征,一个图形绕某点或某轴旋转一定的角度,大小、形状不变,只是位置发生了变化。
【详解】把一个图形逆时针旋转45°,所得的图形与原图形比较大小、形状不变,只是位置发生了变化;
故答案为:C
12.B
【分析】决定旋转后图形的位置的要素:一是旋转中心或轴,二是旋转方向(顺时针或逆时针),三是旋转角度。
【详解】逆时针旋转90°是,与图形A一样;怎么旋转也不能得到图形A;顺时针旋转180°是,与图形a一样;怎么旋转也不能得到图形A。
故答案为:B
13.A
【分析】根据旋转的特征,长方形绕点O顺时针旋转90°后,点O的位置不动,其余各部分均绕此点按相同方向旋转相同的度数,即可画出旋转后的图形。
【详解】如图,
把长方形绕0点顺时针旋转90°后,得到的图形是。
故答案为:A
14.C
【分析】在平面内,将一个图形绕一个定点按某个方向转动一个角度,这样的运动叫做图形的旋转,旋转方向和钟表的指针旋转方向相同,叫顺时针旋转,旋转方向和钟表的指针旋转方向相反,叫逆时针旋转,根据旋转的特征,图形①绕点0顺时针旋转90°即可得到图形②。据此选择即可。
【详解】由分析可知:
将图形①绕点O顺时针旋转90°可以得到图形②。
故答案为:C
15.C
【分析】在平面内,把一个图形围绕某一固定点按顺时针或逆时针方向转动一定的角度的过程,称为旋转。小猴子在A点时,看到房子的图片是,从A点绕房子逆时针转90°时,这时看到房子的图片是,从A点绕房子逆时针转180°时,这时看到房子的图片是,从A点绕房子逆时针转270°时,这时看到房子的图片是;据此解答。
【详解】根据分析得,小猴子从点A起绕房子逆时针转一圈,所看到房子的图片依次为:
。
故答案为:C
16.C
【分析】根据旋转对称图形的概念:把一个图形绕着一个定点旋转一个角度后,与初始图形重合,这种图形叫做旋转对称图形,这个定点叫做旋转对称中心,旋转的角度叫做旋转角。
【详解】A.旋转任意角度都与原图形重合,错误;
B.旋转最小的度数是120°与原图形重合,错误;
C.旋转最小的度数是72°与原图形重合,则旋转120°不能与原图形重合,正确;
故答案为:C
17.√
【分析】钟面指针转动的方向是顺时针方向;一个钟面平均分成12个大格,分针走一圈是360°,那么分针走1大格是360÷12=30°;分针顺时针旋转90°,旋转了3大格,据此解答。
【详解】如图:
360°÷12=30°
90°÷30°=3(格)
钟面上的分针,从12绕中心轴顺时针旋转90°就到了“3”。
原题说法正确。
故答案为:√
18.√
【分析】钟面上有12个大格,时针转一周是360°,是12小时,那么时针一小时旋转的角度是360°÷12=30°。图中时针从3时顺时针旋转到6时,走过了(6-3)小时,再乘时针每小时旋转的角度即可。
【详解】6时-3时=3(小时)
30°×3=90°
图中钟面上的时针绕中心点顺时针方向旋转了90°。
原题说法正确。
故答案为:√
19.√
【分析】钟面指针转动的方向是顺时针方向,钟面1个大格是30°,据此分析。
【详解】从4时到5时,时针转动1个大格,时针顺时针旋转了30°,选项说法正确。
故答案为:√
20.×
【分析】电风扇的扇叶围绕中心转动,这是旋转现象。
【详解】电风扇的扇叶做旋转运动。
故答案为:×
21.(1)见详解;
(2)90°;直角;
(3)16
【分析】(1)以点E为旋转中心,三角形ADE绕点E逆时针旋转90°后,DE和FE重合,在FB上截取FG=DA,连接EG,三角形GFE就是三角形ADE绕点E逆时针旋转90°后的图形;
(2)DEFB是一个正方形,∠DEF是一个直角,则∠1与∠2的和为90°,图形旋转前后对应角的大小相等,∠GEF=∠1,那么∠GEC=90°,有一个角为直角的三角形是直角三角形;
(3)由图可知,AE=GE=4厘米,EC=8厘米,三角形GEC是直角三角形,利用“三角形的面积=底×高÷2”求出三角形GEC的面积就是阴影部分的面积,据此解答。
【详解】(1)分析可知:
(2)分析可知,90°。
∠GEF=∠1
∠GEF+∠2=∠GEC=90°
所以,组合后的阴影部分是一个直角三角形。
(3)4×8÷2
=32÷2
=16(平方厘米)
所以,阴影部分的面积是16平方厘米。
22.(1)6
(2)(3)见详解
【分析】(1)根据平移的特征,三角形部分向右平移6格,即6厘米,平行四边形就变成了长方形。
(2)根据旋转的特征,图三角形ABC绕点B顺时针旋转90°,点B的位置不动,这个图形的各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形;
(3)根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴(虚线)的右边画出左半图的关键对称点,依次连接即可画出这个图形的另一半。
【详解】(1)图中平行四边形沿高分成了两部分,把其中的三角形向右平移6厘米。
(2)把三角形ABC绕B顺时针旋转90°,画出旋转后的图形。
(3)画出图中下方图形的另一半使它成为轴对称图形,这是一个等腰梯形。
23.(1)(3)见详解
(2)直角;6
【分析】(1)用数对表示位置时,通常把竖排叫列,横排叫行。一般情况下,确定第几列时从左往右数,确定第几行时从前往后数。表示列的数在前,表示行的数在后,中间用逗号“,”隔开,数对加上小括号。据此描出各点,连接即可。
(2)C与A在同一列,C与B在同一行,三角形是直角三角形,面积=BC×AC÷2。
(3)作平移后的图形步骤:找点-找出构成图形的关键点;定方向、距离-确定平移方向和平移距离;画线-过关键点沿平移方向画出平行线;定点-由平移的距离确定关键点平移后的对应点的位置;连点-连接对应点。
【详解】(1)(3)如图:
(2)连接后的图形是直角三角形,
3×4÷2
=12÷2
=6(平方厘米)
连接后的图形是直角三角形,它的面积是6cm。
答案第1页,共2页
答案第1页,共2页
5.图形的运动(三) 同步练习 (含答案)
一、填空题
1.图形经过( )时针,旋转( )°后,能将右图填满,正好成为长方形。
2.将△ABC绕点A顺时针旋转90°,与点B对应的点我们记作B’与点C对应的点我们记作C'。
如果点A的位置用数对(5,4)表示,B点用数对(8,6)表示,那么点B'用数对表示为( ),那么点C'用数对表示为( )。
3.
(注意:图在格内所画的竖线、横线都是与格子竖线、横线重合的!)
(1)小帆船先向( )平移了( )格,再向( )平移了( )格。
(2)三角形先向( )平移了( )格,再向( )平移了( )格。
4.从9:00到6:00,时针沿逆时针旋转了( )°。
5.可以看做是由一个基本图形按顺时针或逆时针方向连续经过了( )次旋转,且每次旋转( )°得到的。
6.如图,扇子打开时,扇柄的一侧不动,另一侧绕点O( )时针方向旋转了( )°。
7.钟面上,分针绕中心点从3时30分开始按顺时针方向旋转90°后是( )时( )分。
二、选择题
8.如图,三角形M绕点O顺时针旋转90°得到的图形是( )。
A. B. C.
9.从12:00到12:20,分针绕中心点顺时针旋转了( )。
A.20° B.30° C.120°
10.钟面上,如果分针旋转半圈,那么时针旋转( )。
A.15° B.30° C.90°
11.把一个图形逆时针旋转45°后,所得的图形与原图形相比较( )。
A.变大了 B.变小了 C.大小不变
12.下面的图形中,通过旋转可以得到图形A的是( )。
A.①② B.①③ C.②④
13.把长方形绕0点顺时针旋转90°后,得到的图形是( )。
A. B. C.
14.如图,将图形①经过( )可以得到图形②。
A.向右平移2格 B.向上平移2格 C.绕点O顺时针旋转90°
15.如下图,小猴子从点A起绕房子逆时针转一圈,所看到房子的图片排序正确的是( )。
A.①②③④ B.①③②④ C.③②④①
16.将下列图形绕着各自的中心点旋转120°后,不能与原来的图形重合的是( )。
A. B. C.
三、判断题
17.钟面上的分针,从12绕中心轴顺时针旋转90°就到了“3”。( )
18.图中钟面上的时针绕中心点顺时针方向旋转了90°。( )
19.从4时到5时,时针顺时针旋转了30°。( )
20.电风扇的扇叶做平移运动。( )
四、解答题
21.如图,白色部分DEFB是一个正方形,AE长4厘米,EC长8厘米。阴影部分的面积是多少平方厘米?
提示:怎样把两个阴影部分拼到一起呢?
我们可以这样思考:
(1)将三角形ADE绕点E逆时针旋转90°,画出旋转后的图形。这样两个阴影部分就拼到一起了。
(2)因为( ),所以组合后的阴影部分是一个( )三角形。
(3)旋转后的AE长4厘米,EC长8厘米,阴影部分的面积是( )平方厘米。
22.如图,每个方格的边长表示1厘米。
(1)图中的平行四边形沿高分成了两部分,将涂色的三角形向右平移( )厘米,平行四边形就转化成了长方形。
(2)把三角形ABC绕点B顺时针旋转90°,画出旋转后的图形。
(3)画出图中下方图形的另一半,使它成为轴对称图形。
23.操作。
(1)在如图方格图中描出点A(6,6),点B(3,2),点C(6,2),并顺次连接三点。
(2)连接后的图形是( )三角形,它的面积是( )cm。
(3)画出这个三角形绕点C顺时针旋转90后的图形,并标上A1、B1、C1。
试卷第1页,共3页
试卷第1页,共3页
参考答案
1. 顺 180
【分析】观察右图空白部分的图形应为,才能组成长方形,根据旋转的特征,图形经过顺时针旋转180°后,就能形成这样的图形,据此解答。
【详解】根据分析得,图形经过顺时针,旋转180°后,能将右图填满,正好成为长方形。
2. (7,1) (5,0)
【分析】A点位置不变,先确定出B点和C点绕点A顺时针旋转90°后的点B’和C’,顺次连接得旋转后的图形AB’C’,再用数对表示出B’和C’的位置。
【详解】如图:
点B'用数对表示为(7,1),那么点C'用数对表示为(5,0)。
3.(1) 右 9 下 7
(2) 上 5 左 6
【分析】(1)图中右面的帆船的各点是由左面的帆船的各对应点向右平移9格,再向下平移了7格得到的;
(2)图中上面的三角形的各点是由下面的三角形的各对应点向上平移5格,再向左平移了6格得到的。
【详解】(1)小帆船先向右平移了9格,再向下平移了7格。
(2)三角形先向上平移了5格,再向左平移了6格。
4.90
【分析】在钟表中共有12个大格,则每个大格有360°÷12=30°,因为9:00到6:00共有3个大格,据此选择即可。
【详解】3×30°=90°
则从9:00到6:00,时针沿逆时针旋转了90°。
5. 3 90
【分析】看图,由一个基本图形,旋转之后变成了四个一模一样的图形,所以是经过了三次旋转。再观察发现,每次的旋转角度是90°。
【详解】可以看做是由一个基本图形按顺时针或逆时针方向连续经过了3次旋转,且每次旋转90°得到的。
6. 顺 90
【分析】根据旋转的特征,扇子打开时,将扇子绕O点顺时针旋转90°,点O位置不变,其余各部分均绕此点按相同方向旋转相同度数,即顺时针旋转90°,据此解答。
【详解】扇子打开时,扇柄的一侧不动,另一侧绕点O顺时针方向旋转了90°。
7. 3 45
【分析】钟面上12个数字,以表芯为旋转点,表针转一圈是360°,被12个数字平均分成12份,每一份也就是两数之间夹角是30°。分针绕中心点从3时30分开始按顺时针方向旋转90°,也就是三大格,经过15分钟,旋转后是3:45。
【详解】钟面上,分针绕中心点从3时30分开始按顺时针方向旋转90°后是3时45分。
8.A
【分析】图形的旋转是图形上的每个点在平面上绕着某个固定点旋转固定角度的位置移动,其中对应点到旋转中心的距离相等,对应线段的长度、对应角的大小相等,且旋转前后图形的大小和形状没有改变,三角形M绕点O顺时针旋转90°,点O的位置不动,三角形M的各部分绕点O按相同的方向旋转相同的度数,据此解答。
【详解】A.三角形M绕点O顺时针旋转90°得到;
B.三角形M绕点O逆时针旋转90°得到;
C.三角形M绕点O顺(逆)时针旋转180°得到;
故答案为:A
9.C
【分析】分针绕一周是60分钟,也就是把钟面的圆平均分成60份,一个圆是360°,平均分成60份,先用除法求出一份是多少度,从12:00到12:20是20分钟,也就是其中的20份。用乘法计算即可求出旋转了多少度。
【详解】360°÷60=6°
6°×20=120°
分针绕中心点顺时针旋转了120°。
故答案为:C
10.A
【分析】时针或分针绕钟面旋转一周是360°,整个钟面被平均分成12大格,一个大格是30°,时针一小时旋转一个大格,分针一小时绕钟面旋转一周,如果分针绕钟面旋转半周,一共是半个小时,则分针旋转半个大格,据此解答。
【详解】360°÷12÷2
=30°÷2
=15°
所以,钟面上,如果分针旋转半圈,那么时针旋转15°。
故答案为:A
11.C
【分析】根据旋转图形的特征,一个图形绕某点或某轴旋转一定的角度,大小、形状不变,只是位置发生了变化。
【详解】把一个图形逆时针旋转45°,所得的图形与原图形比较大小、形状不变,只是位置发生了变化;
故答案为:C
12.B
【分析】决定旋转后图形的位置的要素:一是旋转中心或轴,二是旋转方向(顺时针或逆时针),三是旋转角度。
【详解】逆时针旋转90°是,与图形A一样;怎么旋转也不能得到图形A;顺时针旋转180°是,与图形a一样;怎么旋转也不能得到图形A。
故答案为:B
13.A
【分析】根据旋转的特征,长方形绕点O顺时针旋转90°后,点O的位置不动,其余各部分均绕此点按相同方向旋转相同的度数,即可画出旋转后的图形。
【详解】如图,
把长方形绕0点顺时针旋转90°后,得到的图形是。
故答案为:A
14.C
【分析】在平面内,将一个图形绕一个定点按某个方向转动一个角度,这样的运动叫做图形的旋转,旋转方向和钟表的指针旋转方向相同,叫顺时针旋转,旋转方向和钟表的指针旋转方向相反,叫逆时针旋转,根据旋转的特征,图形①绕点0顺时针旋转90°即可得到图形②。据此选择即可。
【详解】由分析可知:
将图形①绕点O顺时针旋转90°可以得到图形②。
故答案为:C
15.C
【分析】在平面内,把一个图形围绕某一固定点按顺时针或逆时针方向转动一定的角度的过程,称为旋转。小猴子在A点时,看到房子的图片是,从A点绕房子逆时针转90°时,这时看到房子的图片是,从A点绕房子逆时针转180°时,这时看到房子的图片是,从A点绕房子逆时针转270°时,这时看到房子的图片是;据此解答。
【详解】根据分析得,小猴子从点A起绕房子逆时针转一圈,所看到房子的图片依次为:
。
故答案为:C
16.C
【分析】根据旋转对称图形的概念:把一个图形绕着一个定点旋转一个角度后,与初始图形重合,这种图形叫做旋转对称图形,这个定点叫做旋转对称中心,旋转的角度叫做旋转角。
【详解】A.旋转任意角度都与原图形重合,错误;
B.旋转最小的度数是120°与原图形重合,错误;
C.旋转最小的度数是72°与原图形重合,则旋转120°不能与原图形重合,正确;
故答案为:C
17.√
【分析】钟面指针转动的方向是顺时针方向;一个钟面平均分成12个大格,分针走一圈是360°,那么分针走1大格是360÷12=30°;分针顺时针旋转90°,旋转了3大格,据此解答。
【详解】如图:
360°÷12=30°
90°÷30°=3(格)
钟面上的分针,从12绕中心轴顺时针旋转90°就到了“3”。
原题说法正确。
故答案为:√
18.√
【分析】钟面上有12个大格,时针转一周是360°,是12小时,那么时针一小时旋转的角度是360°÷12=30°。图中时针从3时顺时针旋转到6时,走过了(6-3)小时,再乘时针每小时旋转的角度即可。
【详解】6时-3时=3(小时)
30°×3=90°
图中钟面上的时针绕中心点顺时针方向旋转了90°。
原题说法正确。
故答案为:√
19.√
【分析】钟面指针转动的方向是顺时针方向,钟面1个大格是30°,据此分析。
【详解】从4时到5时,时针转动1个大格,时针顺时针旋转了30°,选项说法正确。
故答案为:√
20.×
【分析】电风扇的扇叶围绕中心转动,这是旋转现象。
【详解】电风扇的扇叶做旋转运动。
故答案为:×
21.(1)见详解;
(2)90°;直角;
(3)16
【分析】(1)以点E为旋转中心,三角形ADE绕点E逆时针旋转90°后,DE和FE重合,在FB上截取FG=DA,连接EG,三角形GFE就是三角形ADE绕点E逆时针旋转90°后的图形;
(2)DEFB是一个正方形,∠DEF是一个直角,则∠1与∠2的和为90°,图形旋转前后对应角的大小相等,∠GEF=∠1,那么∠GEC=90°,有一个角为直角的三角形是直角三角形;
(3)由图可知,AE=GE=4厘米,EC=8厘米,三角形GEC是直角三角形,利用“三角形的面积=底×高÷2”求出三角形GEC的面积就是阴影部分的面积,据此解答。
【详解】(1)分析可知:
(2)分析可知,90°。
∠GEF=∠1
∠GEF+∠2=∠GEC=90°
所以,组合后的阴影部分是一个直角三角形。
(3)4×8÷2
=32÷2
=16(平方厘米)
所以,阴影部分的面积是16平方厘米。
22.(1)6
(2)(3)见详解
【分析】(1)根据平移的特征,三角形部分向右平移6格,即6厘米,平行四边形就变成了长方形。
(2)根据旋转的特征,图三角形ABC绕点B顺时针旋转90°,点B的位置不动,这个图形的各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形;
(3)根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴(虚线)的右边画出左半图的关键对称点,依次连接即可画出这个图形的另一半。
【详解】(1)图中平行四边形沿高分成了两部分,把其中的三角形向右平移6厘米。
(2)把三角形ABC绕B顺时针旋转90°,画出旋转后的图形。
(3)画出图中下方图形的另一半使它成为轴对称图形,这是一个等腰梯形。
23.(1)(3)见详解
(2)直角;6
【分析】(1)用数对表示位置时,通常把竖排叫列,横排叫行。一般情况下,确定第几列时从左往右数,确定第几行时从前往后数。表示列的数在前,表示行的数在后,中间用逗号“,”隔开,数对加上小括号。据此描出各点,连接即可。
(2)C与A在同一列,C与B在同一行,三角形是直角三角形,面积=BC×AC÷2。
(3)作平移后的图形步骤:找点-找出构成图形的关键点;定方向、距离-确定平移方向和平移距离;画线-过关键点沿平移方向画出平行线;定点-由平移的距离确定关键点平移后的对应点的位置;连点-连接对应点。
【详解】(1)(3)如图:
(2)连接后的图形是直角三角形,
3×4÷2
=12÷2
=6(平方厘米)
连接后的图形是直角三角形,它的面积是6cm。
答案第1页,共2页
答案第1页,共2页
