【备考2023】广西贵港市中考数学模拟试卷1
文档属性
| 名称 | 【备考2023】广西贵港市中考数学模拟试卷1 |  | |
| 格式 | doc | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-10 15:32:09 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
【备考2023】广西贵港市中考数学模拟试卷1
姓名:__________班级:__________考号:__________总分__________
一、选择题(本大题共12小题,每小题3分,共36分.)每小题都给出标号为A.B.C.D.的四个选项,其中只有一个是正确的,请考生用2B铅笔在答题卡上将选定的答案标号涂黑.
1.表示的数一定是( )
A.负数 B.负整数 C.正数或负数 D.以上答案都不对
2.下列各式中,一定是二次根式的是( ).
A. B. C. D.
3.人体内的许多细胞大约都只有0.01mm长,那么用科学记数法表示0.01mm为( ).
A.mm B.mm C.mm D.mm
4.下面是九年一班23名女同学每分钟仰卧起坐的测试情况统计表:
个数/个 35 38 42 45 48
人数 3 5 7 4 4
则该班女同学每分钟仰卧起坐个数的中位数是( )
A.35个 B.38个 C.42个 D.45个
5.下列关系式中,正确的是( )
A. B.
C. D.
6.关于方程的根的说法错误的是( )
A.有两个不相等的实数根 B.两实数根的平方和为
C.两实数根的和为 D.两实数根的积为
7.已知且,则a的取值范围是( )
A. B. C. D.
8.下面计算正确的是( )
A. B.–3÷3×3=–3
C.–3–3=0 D.
9.点A、B、C在上,且四边形为平行四边形,P为上异于A、B、C的一点,则的度数为( )
A. B. C.或 D.或
10.如图,在矩形中,,,对角线交于点O,过点O作交于点E,则的长为( )
A. B. C.1 D.
11.如图,圆柱形容器高为,底面周长为.在容器内壁距离容器底部的点处有一蚊子,此时一只壁虎正好在容器外壁,距离容器上沿的点处,则壁虎捕捉蚊子需爬行的最短距离为( )(不计壁厚)
A. B. C.10 D.20
12.如图,在中,,,将绕点顺时针旋转得到,点A、B的对应点分别是,,点是边的中点,连接,,.则下列结论错误的是( )
A. B.,
C. D.
二、填空题(本大题共6小题,每小题3分,共18分.)
13.若室内的温度是,室外的温度是,则室内温度比室外温度高________.
14.分解因式:=______.
15.如图,ABCD,CE平分∠BCD,∠DCE=16°,则∠B等于______.
16.在一个不透明的盒子中有1个白球和2个红球,它们除颜色外其余都相同,从盒子里任意摸出2个球,则摸出的两个球都是红球的概率是________.
17.已知正方形的边长为,以各边为直径在正方形内画半圆,则所围成的阴影部分(如图的面积为______.
18.如图,过函数图像上的点A,分别向两条坐标轴作垂线,垂足分别为B,C.线段与抛物线的交点为D,则的值为______.
三、解答题(本大题共8小题,满分66分.)解答应写出文字说明、证明过程或演算步骤.
19.先化简,再求值:,其中.
20.如图小方格的边长为1个单位.
(1)画出坐标系,使A、B的坐标分别为(1,1)、(-2,0),并写出点C的坐标;
(2)若将△ABC向右平移4个单位,再向上平移3个单位,得到,在图中画出;
(3)写出△ABC的面积.
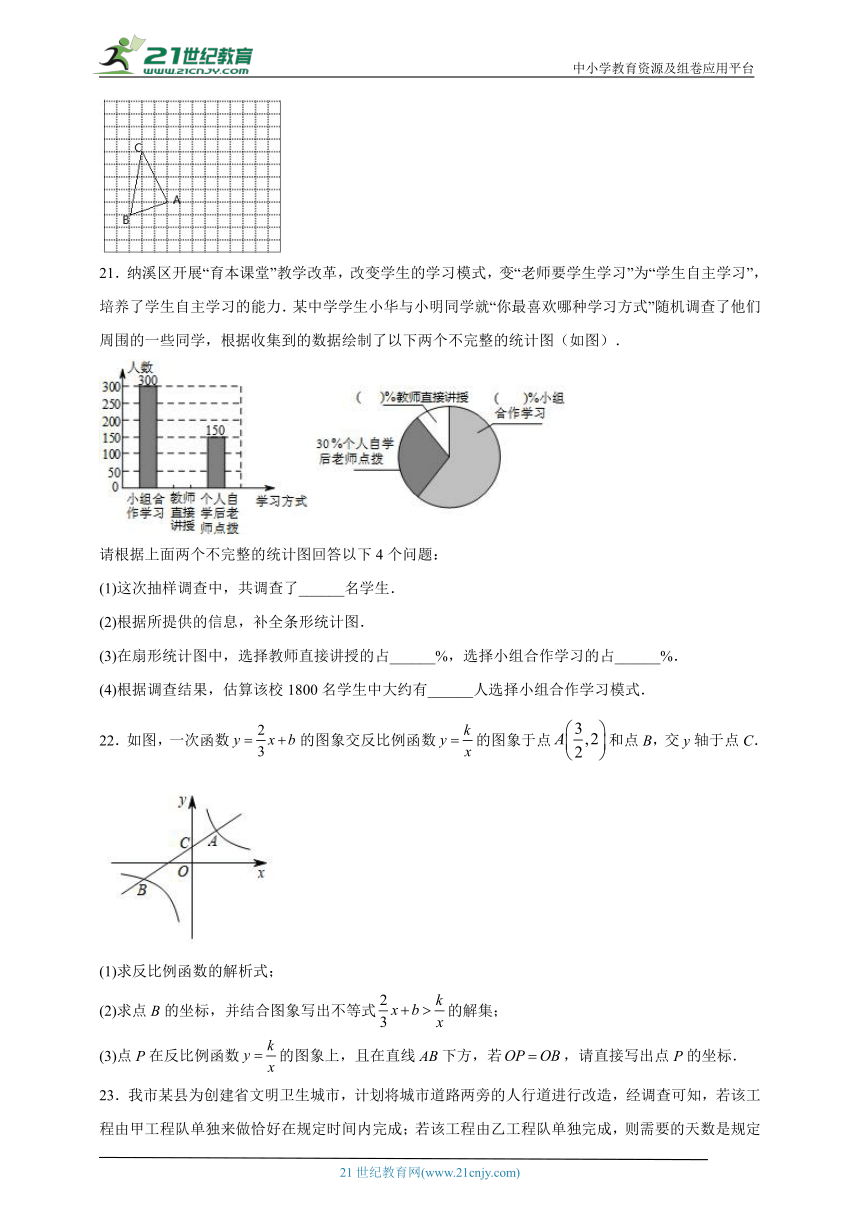
21.纳溪区开展“育本课堂”教学改革,改变学生的学习模式,变“老师要学生学习”为“学生自主学习”,培养了学生自主学习的能力.某中学学生小华与小明同学就“你最喜欢哪种学习方式”随机调查了他们周围的一些同学,根据收集到的数据绘制了以下两个不完整的统计图(如图).
请根据上面两个不完整的统计图回答以下4个问题:
(1)这次抽样调查中,共调查了______名学生.
(2)根据所提供的信息,补全条形统计图.
(3)在扇形统计图中,选择教师直接讲授的占______%,选择小组合作学习的占______%.
(4)根据调查结果,估算该校1800名学生中大约有______人选择小组合作学习模式.
22.如图,一次函数的图象交反比例函数的图象于点和点B,交y轴于点C.
(1)求反比例函数的解析式;
(2)求点B的坐标,并结合图象写出不等式的解集;
(3)点P在反比例函数的图象上,且在直线AB下方,若,请直接写出点P的坐标.
23.我市某县为创建省文明卫生城市,计划将城市道路两旁的人行道进行改造,经调查可知,若该工程由甲工程队单独来做恰好在规定时间内完成;若该工程由乙工程队单独完成,则需要的天数是规定时间的2倍,若甲、乙两工程队合作6天后,余下的工程由甲工程队单独来做还需3天完成.
(1)问该县要求完成这项工程规定的时间是多少天?
(2)已知甲工程队做一天需付给工资5万元,乙工程队做一天需付给工资3万元.现该工程由甲、乙两个工程队合作完成,该县准备了工程工资款65万元.请问该县准备的工程工资款是否够用?
24.已知二次函数y=x2-6x+8.求:
(1)抛物线与x轴和y轴相交的交点坐标;
(2)抛物线的顶点坐标;
(3)画出此抛物线图象,利用图象回答下列问题:
①方程x2-6x+8=0的解是什么?
②x取什么值时,函数值大于0?
③x取什么值时,函数值小于0?
25.如图,在中,,,,点为边上的动点,点从点出发,沿边往运动,当运动到点时停止,若设点运动的时间为秒,点运动的速度为每秒2个单位长度.
(1)当时,______,______;(请直接写出答案)
(2)当为何值时,是直角三角形;(写出解答过程)
(3)求当为何值时,是等腰三角形?并说明理由.
26.如图,在矩形ABCD中, , ,将矩形沿直线EF折叠.使得点A恰好落在BC边上的点G处,且点E、F分别在边AB、AD上(含端点),连接CF.
(1)当 时,求AE的长;
(2)当AF取得最小值时,求折痕EF的长;
(3)连接CF,当 是以CG为底的等腰三角形时,直接写出BG的长.
参考答案:
1.【分析】根据a的取值,即可判断的取值.
解:当a是正数时,是负数;当a是负数时,是正数;当a是正整数时,是负整数;当a是0时,是0,既不是正数也不是负数,故不一定是负数、负整数、正数或负数,故以上答案都不对,
故选:D
【点评】此题考查了有理数,熟练掌握字母表示数的意义是解题的关键.
2.【分析】根据二次根式的定义:形如的式子逐项判断即可.
解:A、缺少条件,不一定是二次根式,本选项不符合题意;
B、为三次根式,不符合二次根式的定义,本选项不符合题意;
C、被开方数,不符合二次根式的定义,本选项不符合题意;
D、,,一定是二次根式,本选项符合题意.
故选:D.
【点评】本题考查了二次根式的定义,属于基础题型,熟知二次根式的概念是关键.
3.【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10-n,与较大数的科学记数法不同的是其所使用的是负整数指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.
解:用科学记数法表示0.01mm为1×10-2mm.
故选:B.
【点评】本题考查用科学记数法表示较小的数,一般形式为a×10-n,其中1≤|a|<10,n为由原数左边起第一个不为零的数字前面的0的个数所决定.
4.【分析】根据中位数的概念解答即可.
解:这组数据按照从小到大的顺序排列,排在12位的数是42.
则中位数为42.
故选:C.
【点评】本题主要考查了中位数的定义,先将数据照从小到大的顺序排列,处于中间位置的数据即为中位数.
5.【分析】根据完全平方公式、平方差公式逐项进行计算即可做出判断.
解:A. ,故A选项错误;
B. ,故B选项错误;
C. ,故C选项错误;
D. ,正确,
故选:D.
【点评】本题考查了完全平方公式、平方差公式,熟记这两个公式是解题的关键.
6.【分析】根据判别式判断方程根的情况,利用根与系数的关系,判断两根之和与两根之积以及两根的平方和.
解:A、,方程有两个不相等的实数根,选项正确,不符合题意;
B、设方程的两个根为:,则:,
∴,选项正确,不符合题意;
C、设方程的两个根为:,则:,选项错误,符合题意;
D、设方程的两个根为:,则:,选项正确,不符合题意;
故选C.
【点评】本题考查一元二次方程判别式与根的个数的关系,以及一元二次方程根与系数的关系.熟练掌握根与系数的关系是解题的关键.
7.【分析】根据不等式的性质把不等式和不等式相加得到即可得到答案.
解:∵,,
∴,
∴,
∴,
故选B.
【点评】本题主要考查了不等式的性质,正确得到是解题的关键.
8.【分析】各项计算得到结果,即可作出判断.
解:A.,故错误;
B.,正确;
C.,故错误;
D.,故错误.
故选:B.
【点评】此题考查了实数的运算,熟练掌握运算法则是解本题的关键.
9.【分析】如图,连接OB,先证明四边形OABC为菱形,再证明△AOB和△BOC都为等边三角形,则△AOB=∠BOC=60°,即∠AOC=∠ABC=120°,讨论:当P点在优弧AC上或当P点在劣弧AC上时,利用圆周角定理可得到∠APC的度数.
解:如图,连接OB,
∵四边形OABC为平行四边形,OA=OC,
∴四边形OABC为菱形,
∴AB=BC=OA=OC=OB,
∴∠AOB=∠BOC=60°,
∴∠AOC=∠ABC=120°,
当P点在优弧AC上时,∠APC=∠AOC=60°;
当P点在劣弧AC上时,∠APC=∠ABC=120°;
即∠APC的度数为60°或120°.
故选C.
【点评】本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.
10.【分析】先利用勾股定理求出对角线的长度,根据矩形对角线互相平分的性质可求出的长度,然后根据相似三角形对应边成比例列方程求解即可.
解:∵在矩形中,,,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
∴,即,
解得.
故选:B
【点评】此题考查勾股定理和相似三角形,解题关键是先通过角等证明相似三角形,然后利用对应边成比例列方程.
11.【分析】将容器侧面展开,建立A关于EF的对称点A′,根据两点之间线段最短可知A′B的长度即为所求.
解:如图:
∵高为12cm,底面周长为,在容器内壁离容器底部3cm的点B处有一蚊子,
此时一只壁虎正好在容器外壁,离容器上沿3cm与蚊子相对的点A处,
∴A′D=8cm,BD=12cm,
∴将容器侧面展开,作A关于EF的对称点A′,
连接A′B,则A′B即为最短距离,
A′B=(cm),
故壁虎捕捉蚊子的最短距离为cm,
故选:A.
【点评】本题考查了平面展开 最短路径问题,将图形展开,利用轴对称的性质和勾股定理进行计算是解题的关键.同时也考查了同学们的创造性思维能力.
12.【分析】根据旋转的性质可判断A;根据直角三角形的性质、三角形外角的性质、平行线的判定方法可判断B;根据平行四边形的判定与性质以及全等三角形的判定与性质可判断C;利用等腰三角形的性质和含30°角的直角三角形的性质可判断D.
解:A.∵将△ABC绕点C顺时针旋转60°得到△DEC,
∴∠BCE=∠ACD=60°,CB=CE,
∴△BCE是等边三角形,
∴BE=BC,故A正确;
B.∵点F是边AC中点,
∴CF=BF=AF=AC,
∵∠BCA=30°,
∴BA=AC,
∴BF=AB=AF=CF,
∴∠FCB=∠FBC=30°,
延长BF交CE于点H,则∠BHE=∠HBC+∠BCH=90°,
∴∠BHE=∠DEC=90°,
∴BF//ED,
∵AB=DE,
∴BF=DE,故B正确.
C.∵BF∥ED,BF=DE,
∴四边形BEDF是平行四边形,
∴BC=BE=DF,
∵AB=CF, BC=DF,AC=CD,
∴△ABC≌△CFD,
∴,故C正确;
D.∵∠ACB=30°, ∠BCE=60°,
∴∠FCG=30°,
∴FG=CG,
∴CG=2FG.
∵∠DCE=∠CDG=30°,
∴DG=CG,
∴DG=2FG.故D错误.
故选D.
【点评】本题考查了旋转的性质,全等三角形的判定与性质,等边三角形的判定与性质,含30°角的直角边等于斜边的一半,以及平行四边形的判定与性质等知识,综合性较强,正确理解旋转性质是解题的关键.
13.【分析】要求室内温度比室外温度高多少,用减法即可.根据有理数的减法法则进行计算:减去一个数即加上这个数的相反数.
解:根据题意,得.
即室内温度比室外温度高.
故答案为:21.
【点评】本题主要考查了有理数的减法法则,解题的关键是熟练掌握有理数的减法法则的内容并会应用.
14.【分析】先提公因式,然后用完全平方公式进行因式分解即可.
解:原式
故答案为:.
【点评】本题考查了综合提公因式与公式法进行因式分解.解题的关键在于正确的运算.
15.【分析】根据角平分线的定义可得∠BCD=2∠DCE,然后根据两直线平行,内错角相等可得∠B=∠BCD.
解:∵CE平分∠BCD,∠DCE=16°,
∴∠BCD=2∠DCE=2×16=32°,
∵ABCD,
∴∠B=∠BCD=32°.
故答案为32°.
【点评】本题考查了平行线的性质,角平分线的定义,熟记性质与概念是解题的关键.
16.【分析】根据已知条件,结合树状图法和概率公式,即可求解.
解:画树状图得:
∵共有6种等可能的结果,摸到的两个球都是红球的有2种情况,
∴摸到的两个球都是红球的概率为:=.
故答案是:.
【点评】此题考查了列表法或树状图法求概率.用到的知识点为:概率=所求情况数与总情况数之比.
17.【分析】仔细分析图形可得阴影部分的面积等于2个以为直径的圆的面积的和再减去1个以为边长的正方形的面积.
解:由图可得阴影部分的面积
故答案为: πa2-a2.
【点评】本题考查圆、正方形的面积公式,解题的关键是读懂题意及图形,找到阴影部分的面积等于2个以为直径的圆的面积的和再减去1个以为边长的正方形的面积的规律.
18.【分析】过点D作,设,则点,,,可得,再求出直线的关系式为,然后联立可得到点D的横坐标为,即,再由,可得,从而得到,即可求解.
解:过点D作,垂足为E,
设,则点,,,
,
设直线的关系式为,把B、C两点坐标代入得,
,,
直线的关系式为,
联立得,
解得:(舍去),,
∴点D的横坐标为,
即,
,
,
,
,
故答案为:.
【点评】本题主要考查了二次函数与一次函数图象的交点问题,平行线分线段成比例,利用数形结合思想解答是解题的关键.
19.【分析】根据分式的乘除法法则,先化简,再代入求值,即可求解.
解:原式=
=
=,
当时,原式=.
【点评】本题主要考查分式的化简求值,掌握分式的乘除法法则,是解题的关键.
20.【分析】(1)利用点A、B的坐标画出直角坐标系,然后写出C点坐标;
(2)利用点平移的坐标变换规律写出A′、B′、C′的坐标,然后描点即可得到△A′B′C′;
(3)用1个矩形的面积分别减去三个直角三角形的面积可计算出△ABC的面积.
解:(1)如图,点C的坐标为(-1,5);
(2)如图,△A′B′C′为所作;
(3)△ABC的面积=3×5-×3×1-×4×2-×5×1=7.
【点评】本题考查了作图-平移变换:确定平移后图形的基本要素有两个:平移方向、平移距离.作图时要先找到图形的关键点,分别把这几个关键点按照平移的方向和距离确定对应点后,再顺次连接对应点即可得到平移后的图形.
21.【分析】(1)从两个统计图中可知,喜欢“个人自学后教师点拨”的有150人,占调查人数的30%,根据频率=频数÷总数即可求出被调查人数;
(2)根据“各组频数之和等于样本容量”可求出喜欢“教师直接讲授”的人数,即可补全条形统计图;
(3)利用各组频率之和等于1可求出喜欢“教师直接讲授”的所占的百分比及喜欢“小组合作选项”所占的百分比;
(4)用样本中喜欢“小组合作学习”所占的百分比估计总体中喜欢“小组合作学习”所占的百分比,进而求出相应的人数即可.
解:(1)由题意可得,本次调查的学生有:150÷30%=500(名),
故答案为:500;
(2)由题意可得,喜欢教师直接传授有:500-300-150=50(名),
补全的条形统计图如图所示;
(3)由题意可得
选择教师传授所占的百分比为:,
选择小组合作学习所占的百分比为:,
故答案为:10,60;
(4)由题意可得,
该校1800名学生中选择合作学习的有:1800×60%=1080(名),
故答案为:1080.
【点评】本题考查了条形统计图、扇形统计图以及用样本估计总体,理解两个统计图中数量之间的关系是解决问题的前提,掌握频率=频数÷总数是正确解答的关键.
22.【分析】(1)、将点A坐标代入反比例函数解析式,即可求解;
(2)、将点A 坐标代入一次函数解析式,求出一次函数解析式,然后联立一次函数和反比例函数解析式,即可求出B点坐标,再根据函数图像即可求出不等式解集;
(3)、求出OB的长度,设P点坐标,用点的距离公式列出方程即可求解.
解:(1)∵反比例函数的图象过点,
则可得: ,
则反比例函数的解析式为: ;
(2)将A点坐标代入一次函数解析式得: ,
解得: ,
,
∵B点为反比例函数和一次函数的交点,
,
解得: ,,
,
由图像可知:当 或 时,一次函数图像在反比例函数上方,
的解集为: 或;
(3)
由题意得: .
设 ,
,
,
,
整理得: ,
解得 或者,
,
在AB下方,
或者 ,
则m取3或-1,
∴P点坐标为或者
【点评】本题考查了待定系数法求一次函数、反比例函数的解析式,一次函数和反比例函数交点,利用函数图像求不等式,由点的坐标求线段长度,熟练掌握函数图像和性质以及由点坐标求线段长度是解题的关键.
23.【分析】(1)本题是工程问题,也就是总工作量、效率与时间问题,根据题意,规定时间就是甲单独需要的时间,所以设规定时间是x天,那么甲单独完成的时间就是x天,乙单独完成的时间为2x,甲乙一天的工作效率分别为,,甲、乙两工程队合作6天的工作量表示为6(+),甲又单独干了3天表示为,没交代具体工作量是多少的情况下,一般是总工作量为1,所以列方程6(+)+=1;(2)由(1)可以知道甲乙分别单独做需要的时间,用工作量除以两队合作一天的工作效率就是二者合作所用的时间,就可以进一步求出所需的工资款,作出判断,是否够用.
解:(1)设规定时间是x天,
根据题意得6(+)+=1,
解得x=12,
经检验:x=12是原方程的解.
答:该县要求完成这项工程规定的时间是12天;
(2)由(1)知,由甲工程队单独做需12天,乙工程队单独做需24天,
则甲乙两工程队合作需要的天数是1÷(+)=8(天),
所需工程工资款为(5+3)×8=64万>63万,
故该县准备的工程工资款不够用.
【点评】本题考查了分式方程的应用,解题的关键是熟练掌握列分式方程解应用题的一般步骤,即①根据题意找出等量关系②列出方程③解出分式方程④检验⑤作答.注意:分式方程的解必须检验.
24.【分析】(1)分别令x=0,y=0即可求得交点坐标.
(2)把函数解析式转化为顶点坐标形势,即可得顶点坐标.
(3)①根据图象与x轴交点可知方程的解;②③根据图象即可得知x的范围.
解:(1)由题意,令y=0,得x2-6x+8=0,
解得x1=2,x2=4.
所以抛物线与x轴交点为(2,0)和(4,0),
令x=0,y=8.
所以抛物线与y轴交点为(0,8),
(2)抛物线解析式可化为:y=x2-6x+8=(x-3)2-1,
所以抛物线的顶点坐标为(3,-1),
(3)如图所示.
①由图象知,x2-6x+8=0的解为x1=2,x2=4.
②当x<2或x>4时,函数值大于0;
③当2<x<4时,函数值小于0;
【点评】本题考查了二次函数图象上点的坐标特征及函数性质,是基础题型.
25.【分析】(1)根据CD=速度×时间列式计算即可得解,利用勾股定理列式求出AC,再根据AD=AC-CD代入数据进行计算即可得解;
(2)分①∠CDB=90°时,利用△ABC的面积列式计算即可求出BD,然后利用勾股定理列式求解得到CD,再根据时间=路程÷速度计算;②∠CBD=90°时,点D和点A重合,然后根据时间=路程÷速度计算即可得解;
(3)分①CD=BD时,过点D作DE⊥BC于E,根据等腰三角形三线合一的性质可得CE=BE,从而得到CD=AD;②CD=BC时,CD=15;③BD=BC时,过点B作BF⊥AC于F,根据等腰三角形三线合一的性质可得CD=2CF,再由(2)的结论解答.
解:(1)t=2时,CD=2×2=4,
∵∠ABC=90°,AB=20,BC=15,
∴AC=,
AD=AC-CD=25-4=21;
故答案为:4,21;
(2)①∠CDB=90°时,AC BDAB BC,
∴BD,
所以CD=,
∴,
解得:(秒);
②∠CBD=90°时,点D和点A重合,
∴,
解得:(秒);
综上所述,当或秒时,△CBD是直角三角形;
(3)①CD=BD时,如图1,过点D作DE⊥BC于E,
则CE=BE,DE∥AB,
∴CD=AD=AC=,
∴,
解得:(秒);
②CD=BC时,CD=15,
∴,
解得:(秒);
③BD=BC时,如图2,过点B作BF⊥AC于F,
同理可得:CF,则CD=2CF=18,
∴,
解得:(秒);
综上所述,当或或秒时,△CBD是等腰三角形.
【点评】本题主要考查了勾股定理,等腰三角形的判定与性质,三角形的面积,(2)(3)难点在于要分情况讨论,作出图形更形象直观.
26.【分析】(1)根据折叠得出AE=EG,据此设AE=EG=x,则有BE=6-x,由勾股定理求解可得;
(2)由FG⊥BC时FG的值最小,即此时AF能取得最小值,显然四边形AEGF是正方形,从而根据勾股定理可得答案;
(3)由△CFG是以FG为一腰的等腰三角形,可知应分两种情况讨论:①FG=FC;②FG=GC;分别求解可得.
解:(1)由折叠易知,,设,则有,
由勾股定理,得,解得,即
(2)由折叠易知,,而当时,FG的值最小,即此时AF能取得最小值,
当时,FG的值最小,即此时AF能取得最小值,
当时,点E与点B重合,
此时四边形AEGF是正方形,
折痕.
(3)由△CFG是以FG为一腰的等腰三角形,可知应分两种情况讨论:
①当FG=FC时,如图2,过F作FH⊥CG于H,
则有:AF=FG=FC,CH=DF=GH
设AF=FG=FC=x,则DF=10-x=CH=GH
在Rt△CFH中
∵CF2=CH2+FH2
∴x2=62+(10-x)2
解得:x=,
∴DF=CH=GH=10-,
即BG=10-×2=,
②当FG=GC时,则有:AF=FG=GC=x,CH=DF=10-x;
∴GH=x-(10-x)=2x-10,
在Rt△FGH中,由勾股定理易得:x2=62+(2x-10)2,
化简得:3x2-40x+136=0,
∵△=(-40)2-4×3×136=-32<0,
∴此方程没有实数根.
综上可知:BG=.
【点评】本题主要考查四边形的综合问题,解题的关键是掌握矩形和翻折变换的性质、正方形的判定与性质、勾股定理、一元二次方程根与系数的关系等知识点,也考查了分类讨论的数学思想.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
【备考2023】广西贵港市中考数学模拟试卷1
姓名:__________班级:__________考号:__________总分__________
一、选择题(本大题共12小题,每小题3分,共36分.)每小题都给出标号为A.B.C.D.的四个选项,其中只有一个是正确的,请考生用2B铅笔在答题卡上将选定的答案标号涂黑.
1.表示的数一定是( )
A.负数 B.负整数 C.正数或负数 D.以上答案都不对
2.下列各式中,一定是二次根式的是( ).
A. B. C. D.
3.人体内的许多细胞大约都只有0.01mm长,那么用科学记数法表示0.01mm为( ).
A.mm B.mm C.mm D.mm
4.下面是九年一班23名女同学每分钟仰卧起坐的测试情况统计表:
个数/个 35 38 42 45 48
人数 3 5 7 4 4
则该班女同学每分钟仰卧起坐个数的中位数是( )
A.35个 B.38个 C.42个 D.45个
5.下列关系式中,正确的是( )
A. B.
C. D.
6.关于方程的根的说法错误的是( )
A.有两个不相等的实数根 B.两实数根的平方和为
C.两实数根的和为 D.两实数根的积为
7.已知且,则a的取值范围是( )
A. B. C. D.
8.下面计算正确的是( )
A. B.–3÷3×3=–3
C.–3–3=0 D.
9.点A、B、C在上,且四边形为平行四边形,P为上异于A、B、C的一点,则的度数为( )
A. B. C.或 D.或
10.如图,在矩形中,,,对角线交于点O,过点O作交于点E,则的长为( )
A. B. C.1 D.
11.如图,圆柱形容器高为,底面周长为.在容器内壁距离容器底部的点处有一蚊子,此时一只壁虎正好在容器外壁,距离容器上沿的点处,则壁虎捕捉蚊子需爬行的最短距离为( )(不计壁厚)
A. B. C.10 D.20
12.如图,在中,,,将绕点顺时针旋转得到,点A、B的对应点分别是,,点是边的中点,连接,,.则下列结论错误的是( )
A. B.,
C. D.
二、填空题(本大题共6小题,每小题3分,共18分.)
13.若室内的温度是,室外的温度是,则室内温度比室外温度高________.
14.分解因式:=______.
15.如图,ABCD,CE平分∠BCD,∠DCE=16°,则∠B等于______.
16.在一个不透明的盒子中有1个白球和2个红球,它们除颜色外其余都相同,从盒子里任意摸出2个球,则摸出的两个球都是红球的概率是________.
17.已知正方形的边长为,以各边为直径在正方形内画半圆,则所围成的阴影部分(如图的面积为______.
18.如图,过函数图像上的点A,分别向两条坐标轴作垂线,垂足分别为B,C.线段与抛物线的交点为D,则的值为______.
三、解答题(本大题共8小题,满分66分.)解答应写出文字说明、证明过程或演算步骤.
19.先化简,再求值:,其中.
20.如图小方格的边长为1个单位.
(1)画出坐标系,使A、B的坐标分别为(1,1)、(-2,0),并写出点C的坐标;
(2)若将△ABC向右平移4个单位,再向上平移3个单位,得到,在图中画出;
(3)写出△ABC的面积.
21.纳溪区开展“育本课堂”教学改革,改变学生的学习模式,变“老师要学生学习”为“学生自主学习”,培养了学生自主学习的能力.某中学学生小华与小明同学就“你最喜欢哪种学习方式”随机调查了他们周围的一些同学,根据收集到的数据绘制了以下两个不完整的统计图(如图).
请根据上面两个不完整的统计图回答以下4个问题:
(1)这次抽样调查中,共调查了______名学生.
(2)根据所提供的信息,补全条形统计图.
(3)在扇形统计图中,选择教师直接讲授的占______%,选择小组合作学习的占______%.
(4)根据调查结果,估算该校1800名学生中大约有______人选择小组合作学习模式.
22.如图,一次函数的图象交反比例函数的图象于点和点B,交y轴于点C.
(1)求反比例函数的解析式;
(2)求点B的坐标,并结合图象写出不等式的解集;
(3)点P在反比例函数的图象上,且在直线AB下方,若,请直接写出点P的坐标.
23.我市某县为创建省文明卫生城市,计划将城市道路两旁的人行道进行改造,经调查可知,若该工程由甲工程队单独来做恰好在规定时间内完成;若该工程由乙工程队单独完成,则需要的天数是规定时间的2倍,若甲、乙两工程队合作6天后,余下的工程由甲工程队单独来做还需3天完成.
(1)问该县要求完成这项工程规定的时间是多少天?
(2)已知甲工程队做一天需付给工资5万元,乙工程队做一天需付给工资3万元.现该工程由甲、乙两个工程队合作完成,该县准备了工程工资款65万元.请问该县准备的工程工资款是否够用?
24.已知二次函数y=x2-6x+8.求:
(1)抛物线与x轴和y轴相交的交点坐标;
(2)抛物线的顶点坐标;
(3)画出此抛物线图象,利用图象回答下列问题:
①方程x2-6x+8=0的解是什么?
②x取什么值时,函数值大于0?
③x取什么值时,函数值小于0?
25.如图,在中,,,,点为边上的动点,点从点出发,沿边往运动,当运动到点时停止,若设点运动的时间为秒,点运动的速度为每秒2个单位长度.
(1)当时,______,______;(请直接写出答案)
(2)当为何值时,是直角三角形;(写出解答过程)
(3)求当为何值时,是等腰三角形?并说明理由.
26.如图,在矩形ABCD中, , ,将矩形沿直线EF折叠.使得点A恰好落在BC边上的点G处,且点E、F分别在边AB、AD上(含端点),连接CF.
(1)当 时,求AE的长;
(2)当AF取得最小值时,求折痕EF的长;
(3)连接CF,当 是以CG为底的等腰三角形时,直接写出BG的长.
参考答案:
1.【分析】根据a的取值,即可判断的取值.
解:当a是正数时,是负数;当a是负数时,是正数;当a是正整数时,是负整数;当a是0时,是0,既不是正数也不是负数,故不一定是负数、负整数、正数或负数,故以上答案都不对,
故选:D
【点评】此题考查了有理数,熟练掌握字母表示数的意义是解题的关键.
2.【分析】根据二次根式的定义:形如的式子逐项判断即可.
解:A、缺少条件,不一定是二次根式,本选项不符合题意;
B、为三次根式,不符合二次根式的定义,本选项不符合题意;
C、被开方数,不符合二次根式的定义,本选项不符合题意;
D、,,一定是二次根式,本选项符合题意.
故选:D.
【点评】本题考查了二次根式的定义,属于基础题型,熟知二次根式的概念是关键.
3.【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10-n,与较大数的科学记数法不同的是其所使用的是负整数指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.
解:用科学记数法表示0.01mm为1×10-2mm.
故选:B.
【点评】本题考查用科学记数法表示较小的数,一般形式为a×10-n,其中1≤|a|<10,n为由原数左边起第一个不为零的数字前面的0的个数所决定.
4.【分析】根据中位数的概念解答即可.
解:这组数据按照从小到大的顺序排列,排在12位的数是42.
则中位数为42.
故选:C.
【点评】本题主要考查了中位数的定义,先将数据照从小到大的顺序排列,处于中间位置的数据即为中位数.
5.【分析】根据完全平方公式、平方差公式逐项进行计算即可做出判断.
解:A. ,故A选项错误;
B. ,故B选项错误;
C. ,故C选项错误;
D. ,正确,
故选:D.
【点评】本题考查了完全平方公式、平方差公式,熟记这两个公式是解题的关键.
6.【分析】根据判别式判断方程根的情况,利用根与系数的关系,判断两根之和与两根之积以及两根的平方和.
解:A、,方程有两个不相等的实数根,选项正确,不符合题意;
B、设方程的两个根为:,则:,
∴,选项正确,不符合题意;
C、设方程的两个根为:,则:,选项错误,符合题意;
D、设方程的两个根为:,则:,选项正确,不符合题意;
故选C.
【点评】本题考查一元二次方程判别式与根的个数的关系,以及一元二次方程根与系数的关系.熟练掌握根与系数的关系是解题的关键.
7.【分析】根据不等式的性质把不等式和不等式相加得到即可得到答案.
解:∵,,
∴,
∴,
∴,
故选B.
【点评】本题主要考查了不等式的性质,正确得到是解题的关键.
8.【分析】各项计算得到结果,即可作出判断.
解:A.,故错误;
B.,正确;
C.,故错误;
D.,故错误.
故选:B.
【点评】此题考查了实数的运算,熟练掌握运算法则是解本题的关键.
9.【分析】如图,连接OB,先证明四边形OABC为菱形,再证明△AOB和△BOC都为等边三角形,则△AOB=∠BOC=60°,即∠AOC=∠ABC=120°,讨论:当P点在优弧AC上或当P点在劣弧AC上时,利用圆周角定理可得到∠APC的度数.
解:如图,连接OB,
∵四边形OABC为平行四边形,OA=OC,
∴四边形OABC为菱形,
∴AB=BC=OA=OC=OB,
∴∠AOB=∠BOC=60°,
∴∠AOC=∠ABC=120°,
当P点在优弧AC上时,∠APC=∠AOC=60°;
当P点在劣弧AC上时,∠APC=∠ABC=120°;
即∠APC的度数为60°或120°.
故选C.
【点评】本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.
10.【分析】先利用勾股定理求出对角线的长度,根据矩形对角线互相平分的性质可求出的长度,然后根据相似三角形对应边成比例列方程求解即可.
解:∵在矩形中,,,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
∴,即,
解得.
故选:B
【点评】此题考查勾股定理和相似三角形,解题关键是先通过角等证明相似三角形,然后利用对应边成比例列方程.
11.【分析】将容器侧面展开,建立A关于EF的对称点A′,根据两点之间线段最短可知A′B的长度即为所求.
解:如图:
∵高为12cm,底面周长为,在容器内壁离容器底部3cm的点B处有一蚊子,
此时一只壁虎正好在容器外壁,离容器上沿3cm与蚊子相对的点A处,
∴A′D=8cm,BD=12cm,
∴将容器侧面展开,作A关于EF的对称点A′,
连接A′B,则A′B即为最短距离,
A′B=(cm),
故壁虎捕捉蚊子的最短距离为cm,
故选:A.
【点评】本题考查了平面展开 最短路径问题,将图形展开,利用轴对称的性质和勾股定理进行计算是解题的关键.同时也考查了同学们的创造性思维能力.
12.【分析】根据旋转的性质可判断A;根据直角三角形的性质、三角形外角的性质、平行线的判定方法可判断B;根据平行四边形的判定与性质以及全等三角形的判定与性质可判断C;利用等腰三角形的性质和含30°角的直角三角形的性质可判断D.
解:A.∵将△ABC绕点C顺时针旋转60°得到△DEC,
∴∠BCE=∠ACD=60°,CB=CE,
∴△BCE是等边三角形,
∴BE=BC,故A正确;
B.∵点F是边AC中点,
∴CF=BF=AF=AC,
∵∠BCA=30°,
∴BA=AC,
∴BF=AB=AF=CF,
∴∠FCB=∠FBC=30°,
延长BF交CE于点H,则∠BHE=∠HBC+∠BCH=90°,
∴∠BHE=∠DEC=90°,
∴BF//ED,
∵AB=DE,
∴BF=DE,故B正确.
C.∵BF∥ED,BF=DE,
∴四边形BEDF是平行四边形,
∴BC=BE=DF,
∵AB=CF, BC=DF,AC=CD,
∴△ABC≌△CFD,
∴,故C正确;
D.∵∠ACB=30°, ∠BCE=60°,
∴∠FCG=30°,
∴FG=CG,
∴CG=2FG.
∵∠DCE=∠CDG=30°,
∴DG=CG,
∴DG=2FG.故D错误.
故选D.
【点评】本题考查了旋转的性质,全等三角形的判定与性质,等边三角形的判定与性质,含30°角的直角边等于斜边的一半,以及平行四边形的判定与性质等知识,综合性较强,正确理解旋转性质是解题的关键.
13.【分析】要求室内温度比室外温度高多少,用减法即可.根据有理数的减法法则进行计算:减去一个数即加上这个数的相反数.
解:根据题意,得.
即室内温度比室外温度高.
故答案为:21.
【点评】本题主要考查了有理数的减法法则,解题的关键是熟练掌握有理数的减法法则的内容并会应用.
14.【分析】先提公因式,然后用完全平方公式进行因式分解即可.
解:原式
故答案为:.
【点评】本题考查了综合提公因式与公式法进行因式分解.解题的关键在于正确的运算.
15.【分析】根据角平分线的定义可得∠BCD=2∠DCE,然后根据两直线平行,内错角相等可得∠B=∠BCD.
解:∵CE平分∠BCD,∠DCE=16°,
∴∠BCD=2∠DCE=2×16=32°,
∵ABCD,
∴∠B=∠BCD=32°.
故答案为32°.
【点评】本题考查了平行线的性质,角平分线的定义,熟记性质与概念是解题的关键.
16.【分析】根据已知条件,结合树状图法和概率公式,即可求解.
解:画树状图得:
∵共有6种等可能的结果,摸到的两个球都是红球的有2种情况,
∴摸到的两个球都是红球的概率为:=.
故答案是:.
【点评】此题考查了列表法或树状图法求概率.用到的知识点为:概率=所求情况数与总情况数之比.
17.【分析】仔细分析图形可得阴影部分的面积等于2个以为直径的圆的面积的和再减去1个以为边长的正方形的面积.
解:由图可得阴影部分的面积
故答案为: πa2-a2.
【点评】本题考查圆、正方形的面积公式,解题的关键是读懂题意及图形,找到阴影部分的面积等于2个以为直径的圆的面积的和再减去1个以为边长的正方形的面积的规律.
18.【分析】过点D作,设,则点,,,可得,再求出直线的关系式为,然后联立可得到点D的横坐标为,即,再由,可得,从而得到,即可求解.
解:过点D作,垂足为E,
设,则点,,,
,
设直线的关系式为,把B、C两点坐标代入得,
,,
直线的关系式为,
联立得,
解得:(舍去),,
∴点D的横坐标为,
即,
,
,
,
,
故答案为:.
【点评】本题主要考查了二次函数与一次函数图象的交点问题,平行线分线段成比例,利用数形结合思想解答是解题的关键.
19.【分析】根据分式的乘除法法则,先化简,再代入求值,即可求解.
解:原式=
=
=,
当时,原式=.
【点评】本题主要考查分式的化简求值,掌握分式的乘除法法则,是解题的关键.
20.【分析】(1)利用点A、B的坐标画出直角坐标系,然后写出C点坐标;
(2)利用点平移的坐标变换规律写出A′、B′、C′的坐标,然后描点即可得到△A′B′C′;
(3)用1个矩形的面积分别减去三个直角三角形的面积可计算出△ABC的面积.
解:(1)如图,点C的坐标为(-1,5);
(2)如图,△A′B′C′为所作;
(3)△ABC的面积=3×5-×3×1-×4×2-×5×1=7.
【点评】本题考查了作图-平移变换:确定平移后图形的基本要素有两个:平移方向、平移距离.作图时要先找到图形的关键点,分别把这几个关键点按照平移的方向和距离确定对应点后,再顺次连接对应点即可得到平移后的图形.
21.【分析】(1)从两个统计图中可知,喜欢“个人自学后教师点拨”的有150人,占调查人数的30%,根据频率=频数÷总数即可求出被调查人数;
(2)根据“各组频数之和等于样本容量”可求出喜欢“教师直接讲授”的人数,即可补全条形统计图;
(3)利用各组频率之和等于1可求出喜欢“教师直接讲授”的所占的百分比及喜欢“小组合作选项”所占的百分比;
(4)用样本中喜欢“小组合作学习”所占的百分比估计总体中喜欢“小组合作学习”所占的百分比,进而求出相应的人数即可.
解:(1)由题意可得,本次调查的学生有:150÷30%=500(名),
故答案为:500;
(2)由题意可得,喜欢教师直接传授有:500-300-150=50(名),
补全的条形统计图如图所示;
(3)由题意可得
选择教师传授所占的百分比为:,
选择小组合作学习所占的百分比为:,
故答案为:10,60;
(4)由题意可得,
该校1800名学生中选择合作学习的有:1800×60%=1080(名),
故答案为:1080.
【点评】本题考查了条形统计图、扇形统计图以及用样本估计总体,理解两个统计图中数量之间的关系是解决问题的前提,掌握频率=频数÷总数是正确解答的关键.
22.【分析】(1)、将点A坐标代入反比例函数解析式,即可求解;
(2)、将点A 坐标代入一次函数解析式,求出一次函数解析式,然后联立一次函数和反比例函数解析式,即可求出B点坐标,再根据函数图像即可求出不等式解集;
(3)、求出OB的长度,设P点坐标,用点的距离公式列出方程即可求解.
解:(1)∵反比例函数的图象过点,
则可得: ,
则反比例函数的解析式为: ;
(2)将A点坐标代入一次函数解析式得: ,
解得: ,
,
∵B点为反比例函数和一次函数的交点,
,
解得: ,,
,
由图像可知:当 或 时,一次函数图像在反比例函数上方,
的解集为: 或;
(3)
由题意得: .
设 ,
,
,
,
整理得: ,
解得 或者,
,
在AB下方,
或者 ,
则m取3或-1,
∴P点坐标为或者
【点评】本题考查了待定系数法求一次函数、反比例函数的解析式,一次函数和反比例函数交点,利用函数图像求不等式,由点的坐标求线段长度,熟练掌握函数图像和性质以及由点坐标求线段长度是解题的关键.
23.【分析】(1)本题是工程问题,也就是总工作量、效率与时间问题,根据题意,规定时间就是甲单独需要的时间,所以设规定时间是x天,那么甲单独完成的时间就是x天,乙单独完成的时间为2x,甲乙一天的工作效率分别为,,甲、乙两工程队合作6天的工作量表示为6(+),甲又单独干了3天表示为,没交代具体工作量是多少的情况下,一般是总工作量为1,所以列方程6(+)+=1;(2)由(1)可以知道甲乙分别单独做需要的时间,用工作量除以两队合作一天的工作效率就是二者合作所用的时间,就可以进一步求出所需的工资款,作出判断,是否够用.
解:(1)设规定时间是x天,
根据题意得6(+)+=1,
解得x=12,
经检验:x=12是原方程的解.
答:该县要求完成这项工程规定的时间是12天;
(2)由(1)知,由甲工程队单独做需12天,乙工程队单独做需24天,
则甲乙两工程队合作需要的天数是1÷(+)=8(天),
所需工程工资款为(5+3)×8=64万>63万,
故该县准备的工程工资款不够用.
【点评】本题考查了分式方程的应用,解题的关键是熟练掌握列分式方程解应用题的一般步骤,即①根据题意找出等量关系②列出方程③解出分式方程④检验⑤作答.注意:分式方程的解必须检验.
24.【分析】(1)分别令x=0,y=0即可求得交点坐标.
(2)把函数解析式转化为顶点坐标形势,即可得顶点坐标.
(3)①根据图象与x轴交点可知方程的解;②③根据图象即可得知x的范围.
解:(1)由题意,令y=0,得x2-6x+8=0,
解得x1=2,x2=4.
所以抛物线与x轴交点为(2,0)和(4,0),
令x=0,y=8.
所以抛物线与y轴交点为(0,8),
(2)抛物线解析式可化为:y=x2-6x+8=(x-3)2-1,
所以抛物线的顶点坐标为(3,-1),
(3)如图所示.
①由图象知,x2-6x+8=0的解为x1=2,x2=4.
②当x<2或x>4时,函数值大于0;
③当2<x<4时,函数值小于0;
【点评】本题考查了二次函数图象上点的坐标特征及函数性质,是基础题型.
25.【分析】(1)根据CD=速度×时间列式计算即可得解,利用勾股定理列式求出AC,再根据AD=AC-CD代入数据进行计算即可得解;
(2)分①∠CDB=90°时,利用△ABC的面积列式计算即可求出BD,然后利用勾股定理列式求解得到CD,再根据时间=路程÷速度计算;②∠CBD=90°时,点D和点A重合,然后根据时间=路程÷速度计算即可得解;
(3)分①CD=BD时,过点D作DE⊥BC于E,根据等腰三角形三线合一的性质可得CE=BE,从而得到CD=AD;②CD=BC时,CD=15;③BD=BC时,过点B作BF⊥AC于F,根据等腰三角形三线合一的性质可得CD=2CF,再由(2)的结论解答.
解:(1)t=2时,CD=2×2=4,
∵∠ABC=90°,AB=20,BC=15,
∴AC=,
AD=AC-CD=25-4=21;
故答案为:4,21;
(2)①∠CDB=90°时,AC BDAB BC,
∴BD,
所以CD=,
∴,
解得:(秒);
②∠CBD=90°时,点D和点A重合,
∴,
解得:(秒);
综上所述,当或秒时,△CBD是直角三角形;
(3)①CD=BD时,如图1,过点D作DE⊥BC于E,
则CE=BE,DE∥AB,
∴CD=AD=AC=,
∴,
解得:(秒);
②CD=BC时,CD=15,
∴,
解得:(秒);
③BD=BC时,如图2,过点B作BF⊥AC于F,
同理可得:CF,则CD=2CF=18,
∴,
解得:(秒);
综上所述,当或或秒时,△CBD是等腰三角形.
【点评】本题主要考查了勾股定理,等腰三角形的判定与性质,三角形的面积,(2)(3)难点在于要分情况讨论,作出图形更形象直观.
26.【分析】(1)根据折叠得出AE=EG,据此设AE=EG=x,则有BE=6-x,由勾股定理求解可得;
(2)由FG⊥BC时FG的值最小,即此时AF能取得最小值,显然四边形AEGF是正方形,从而根据勾股定理可得答案;
(3)由△CFG是以FG为一腰的等腰三角形,可知应分两种情况讨论:①FG=FC;②FG=GC;分别求解可得.
解:(1)由折叠易知,,设,则有,
由勾股定理,得,解得,即
(2)由折叠易知,,而当时,FG的值最小,即此时AF能取得最小值,
当时,FG的值最小,即此时AF能取得最小值,
当时,点E与点B重合,
此时四边形AEGF是正方形,
折痕.
(3)由△CFG是以FG为一腰的等腰三角形,可知应分两种情况讨论:
①当FG=FC时,如图2,过F作FH⊥CG于H,
则有:AF=FG=FC,CH=DF=GH
设AF=FG=FC=x,则DF=10-x=CH=GH
在Rt△CFH中
∵CF2=CH2+FH2
∴x2=62+(10-x)2
解得:x=,
∴DF=CH=GH=10-,
即BG=10-×2=,
②当FG=GC时,则有:AF=FG=GC=x,CH=DF=10-x;
∴GH=x-(10-x)=2x-10,
在Rt△FGH中,由勾股定理易得:x2=62+(2x-10)2,
化简得:3x2-40x+136=0,
∵△=(-40)2-4×3×136=-32<0,
∴此方程没有实数根.
综上可知:BG=.
【点评】本题主要考查四边形的综合问题,解题的关键是掌握矩形和翻折变换的性质、正方形的判定与性质、勾股定理、一元二次方程根与系数的关系等知识点,也考查了分类讨论的数学思想.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
