【备考2023】广西玉林市中考数学模拟试卷2(含解析)
文档属性
| 名称 | 【备考2023】广西玉林市中考数学模拟试卷2(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-10 15:32:26 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
【备考2023】广西玉林市中考数学模拟试卷2
姓名:__________班级:__________考号:__________总分__________
一、选择题(本大题共12小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的,把正确答案的标号填(涂)在答题卡内相应的位置上.)
1.中新网北京2021年4月2日电,截至4月2日15时,北京累计接种新冠疫苗人数累计接种新冠疫苗超16 000 000剂次.数据16 000 000可用科学记数法表示为( )
A.16×106 B.1.6×107 C.0.16×108 D.1.6×106
2.现有一组数据:2,3,3,4,4,5,6,则下列说法正确的是( )
A.众数是3 B.众数是4 C.中位数是3.5 D.中位数是4
3.一个几何体的俯视图如图所示,其中的数字表示该位置上小正方体的个数,那么这个几何体的主视图是( )
A. B. C. D.
4.在计算时,佳佳的板演过程如下:
解:原式.
老师问:“佳佳同学在解答过程中运用了哪些运算律?”
甲同学回答说:“佳佳在解答过程中运用了加法交换律”;
乙同学回答说:“佳佳在解答过程中运用了加法结合律”;
丙同学回答说:“佳佳在解答过程中既运用了加法交换律,也运用了加法结合律”.
下列对甲、乙、丙三名同学说法判断正确的是( )
A.甲同学说的对 B.乙同学说的对
C.丙同学说的对 D.甲、乙、丙说的都不对
5.下列计算正确的是( )
A. B.
C. D.
6.在Rt△ABC 中,∠C=90°,,AB=5cm,则AC的长度是( )
A.3 cm B.4 cm C.5 cm D.6 cm
7.下面事件是随机事件的是( )
A.掷一枚硬币,出现反面
B.在标准大气压下,水加热到8℃时会沸腾
C.实数的绝对值不小于零
D.如果a,b是实数,那么a b=b a
8.如图,的直径与弦交于点E,若B为的中点,则下列说法错误的是( ).
A. B. C. D.
9.已知x1,x2是一元二次方程x2﹣2x-3=0的两根,则x1+x2的值是( )
A.0 B.2 C.-2 D.4
10.如图,已知矩形,下列条件能使矩形成为正方形的是( )
A. B. C. D.
11.观察下列四个图形组成的一组图形,发现它们是按照一定规律排列的,依此规律排列下去,第10个图形共有( )个点组成
A.26 B.27 C.28 D.29
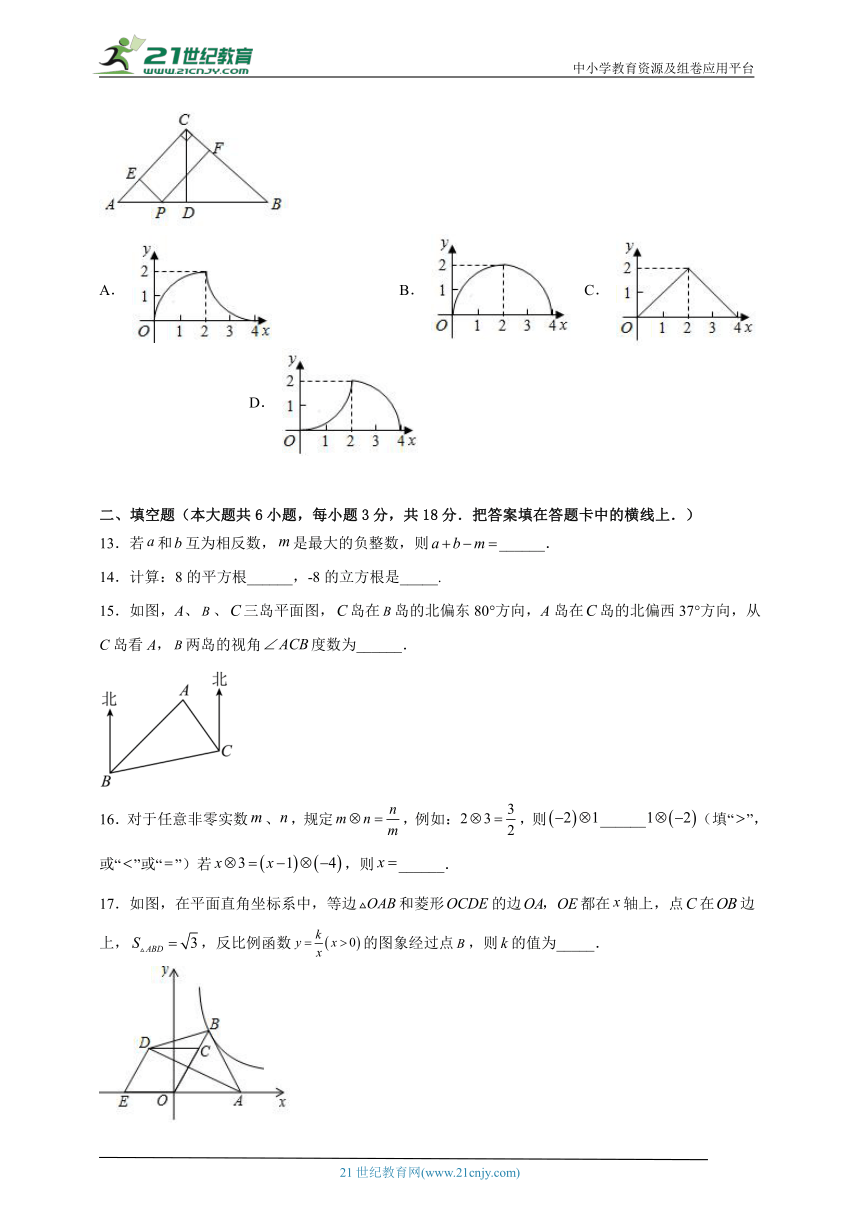
12.如图,在中,,,于点.点从点出发,沿的路径运动,运动到点停止,过点作于点,作于点.设点运动的路程为,四边形的面积为,则能反映与之间函数关系的图象是( )
A. B. C. D.
二、填空题(本大题共6小题,每小题3分,共18分.把答案填在答题卡中的横线上.)
13.若和互为相反数,是最大的负整数,则______.
14.计算:8的平方根______,-8的立方根是_____.
15.如图,A、、三岛平面图,岛在岛的北偏东80°方向,A岛在岛的北偏西37°方向,从C岛看A,两岛的视角度数为______.
16.对于任意非零实数、,规定,例如:,则______(填“”,或“”或“”)若,则______.
17.如图,在平面直角坐标系中,等边和菱形的边都在轴上,点在边上,,反比例函数的图象经过点,则的值为_____.
18.如图,在每个小正方形的边长为1的网格中,上的点,圆心均在格点上,
(1)_____________;
(2)若点是上的一个动点,连接,将绕点逆时针旋转得到,连,当线段最长时,点的对应点为点,点的对应点为点,请用无刻度的直尺,在如图所示的网格中,画出点,,并简要说明点,的位置是如何找到的(不要求证明)____________________.
三、解答题(本大题共8小题,满分共66分.解答应写出证明过程或演算步骤(含相应的文字说明).将解答写在答题卡上)
19.计算:(1)
(2)解方程组.
20.先化简,后求值:;其中.
21.现有两个不透明的袋子,一个装有2个红球,1个白球,一个装有1个黄球,2个红球,这些球除颜色外完全相同,从两个袋子中各随机摸出一个球,利用树状图或列表的方法,求摸出的两个球颜色相同的概率.
22.如图,在平行四边形ABCD中,AC,BD相交于点O,点E在BC上,AE交BD于F.
(1)若E是靠近点B的三等分点,求;①的值;②△BEF与△DAF的面积比;
(2)当时,求的值.
23.如图,已知正方形ABCD中,AB=4,点E,F在对角线BD上,AE∥CF.
(1)求证:△ABE≌△CDF;
(2)若∠ABE=2∠BAE,求DF的长.
24.2012年5月20日是第23个中国学生营养日,某校社会实践小组开展活动,调查快餐营养情况,他们从食品安全监督部门获取了一份快餐的信息.根据信息,解答下列问题.
信息:
1.快餐的成分:蛋白质、脂肪、矿物质、碳水化合物;
2.快餐总质量为400克;
3.脂肪所占的百分比为5%;
4.所含蛋白质质量是矿物质质量的4倍.
(1)求这份快餐中所含脂肪质量;
(2)若碳水化合物占快餐总质量的40%,求这份快餐所含蛋白质的质量;
(3)若这份快餐中蛋白质和碳水化合物所占百分比的和是85%,求其中所含碳水化合物的质量.
25.阅读下面材料,完成后面题目.
0°-360°间的角的三角函数
在初中,我们学习过锐角的正弦、余弦、正切和余切四种三角函数,即在图1所示的直角三角形ABC,∠A是锐角,那么sinA=,cosA=,tanA=,cotA=
为了研究需要,我们再从另一个角度来规定一个角的三角函数的意义:
设有一个角α,我们以它的顶点作为原点,以它的始边作为x轴的正半轴ox,建立直角坐标系(图2),在角α的终边上任取一点P,它的横坐标是x,纵坐标是y,点P和原点(0,0)的距离为r=(r总是正的),然后把角α的三角函数规定为:sinα=,cosα=,tanα=,cotα=
我们知道,图1的四个比值的大小与角A的大小有关,而与直角三角形的大小无关,同样图2中四个比值的大小也仅与角α的大小有关,而与点P在角α的终边位置无关.
比较图1与图2,可以看出一个角的三角函数的意义的两种规定实际上是一样的,根据第二种定义回答下列问题.
(1)若90°<α<180°,则角α的三角函数值sinα、cosα、tanα、cotα,其中取正值的是哪几个?
(2)若角α的终边与直线y=2x重合,求sinα+cosα的值.
(3)若角α是钝角,其终边上一点P(x,),且cosα=x,求tanα的值.
(4)若0°≤α≤90°,求sinα+cosα的取值范围.
26.(如图 1,若抛物线 l1的顶点 A 在抛物线 l2上,抛物线 l2的顶点 B 也在抛物线 l1上(点 A 与点 B 不重合).我们称抛物线 l1,l2互为“友好”抛物线,一条抛物线的“友 好”抛物线可以有多条.
(1)如图2,抛物线 l3: 与y 轴交于点C,点D与点C关于抛物线的对称轴对称,则点 D 的坐标为 ;
(2)求以点 D 为顶点的 l3的“友好”抛物线 l4的表达式,并指出 l3与 l4中y 同时随x增大而增大的自变量的取值范围;
(3)若抛物线 y=a1(x-m)2+n 的任意一条“友好”抛物线的表达式为 y=a2(x-h)2+k, 写出 a1与a2的关系式,并说明理由.
参考答案:
1.【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.
解:将16 000 000用科学记数法表示为1.6×107.
故选:B.
【点评】本题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.
2.【分析】根据求出这组数据的众数和中位数即可求解.
解:数据2,3,3,4,4,5,6的众数是3和4,中位数是4.
故选:D
【点评】本题考查了求一组数据的众数和中位数,众数是指一组数据中出现次数最多的数,中位数是指将数据排序后处于中间位置是数,熟知众数和中位数的意义是解题关键.
3.【分析】一一对应即可.
解:最左边有一个,中间有两个,最右边有三个,所以选A.
【点评】理解立体几何的概念是解题的关键.
4.【分析】根据加法运算律的定义进行解答即可.
解:由到既运用了加法交换律,也运用了加法结合律,所以丙同学说的对,故C正确.
故选:C.
【点评】本题主要考查了加法的交换律和结合律,熟记加法交换律和结合律,,,是解题的关键.
5.【分析】根据合并同类项的方法逐项计算即可.
解:A.a与b不是同类项,不能合并,故不正确;
B.,故不正确;
C.,故不正确;
D.,正确;
故选D.
【点评】本题考查了同类项的定义及合并同类项,熟练掌握合并同类项的方法是解答本题的关键.所含字母相同,并且相同字母的指数也相同的项,叫做同类项;合并同类项时,把同类项的系数相加,所得和作为合并后的系数,字母和字母的指数不变.
6.【分析】根据三角函数的定义求得BC和AB的比值,设出BC、AB,然后利用勾股定理计算即可;
解:∵,
∴设,,
又∵AB=5cm,
∴,
∴,
∴,
∴;
故选B.
【点评】本题主要考查了锐角三角函数与勾股定理,准确计算是解题的关键.
7.【分析】直接利用随机事件以及不可能事件和必然事件的定义分析得出答案.
解:A、掷一枚硬币,出现反面,是随机事件,符合题意;
B、在标准大气压下,水加热到8℃时会沸腾,是不可能事件,不合题意;
C、实数的绝对值不小于零,是必然事件,不合题意;
D、如果a,b是实数,那么a b=b a,是必然事件,不合题意;
故选:A.
【点评】本题考查随机事件的判断,是基础题,解题时要认真审题,注意随机事件的定义的合理运用.
8.【分析】根据垂径定理对各选项进行逐一分析即可.
解:∵的直径与弦交于点E, B为的中点,
∴,,故A,C,D选项正确,
不能得出,故B选项不正确,
故选:B.
【点评】本题考查的是垂径定理的推理,掌握垂径定理是解题的关键.一条直线如果具有①经过圆心,②垂直于弦,③平分弦(被平分的弦不是直径),④平分弦所对的优弧,⑤平分弦所对的劣弧这五条中的任意两条,则必然具备其余的三条,简称“知二推三”.
9.【分析】直接根据根与系数的关系进行求解,即可得到答案.
解:∵x1,x2是一元二次方程x2﹣2x3=0的两根,
∴,
故选:B.
【点评】本题考查了一元二次方程的根与系数的关系,解题的关键是掌握根与系数的关系进行解题.
10.【分析】已知四边形是矩形,要使它成为正方形只有两种方法:(1)一组邻边相等;(2)对角线互相垂直,据此求解即可.
解:∵四边形是矩形,
∴当或当或或或时,四边形是正方形;
故选:B.
【点评】本题主要考查了正方形的判定,熟练地掌握正方形的判定方法是解题的关键.(1)一组邻边相等的矩形是正方形;(2)对角线互相垂直的矩形是正方形.
11.【分析】观察图形,在1个点的基础上,依次多3个;根据其中的规律,用字母表示即可,再把字母的值为10代入计算即可.
解:∵第1个图形为1个点,
第2个图形为1+3=4个点,
第3个图形为1+3+3=7个点,
第3个图形为1+3+3=7个点,
第4个图形为1+3+3+3=10个点,
……,
∴第n个图形为1+3=个点,
当时,
故选C
【点评】本题主要考查学生对图形的变化类的知识点的理解和掌握,此题的关键是注意发现前后图形中的数量之间的关系.
12.【分析】分两段来分析:①点P从点A出发运动到点D时,写出此段的函数解析式,则可排除C和D;②P点过了D点向C点运动,作出图形,写出此阶段的函数解析式,根据图象的开口方向可得答案.
解:∵,,
∴,,
又∵,
∴,,
∵,,
∴四边形是矩形,
I.当P在线段AD上时,即时,如解图1
∴,
∴,
∴四边形的面积为,此阶段函数图象是抛物线,开口方向向下,故选项CD错误;
II.当P在线段CD上时,即时,如解图2:
依题意得:,
∵,,
∴,
∴,
∴四边形的面积为,此阶段函数图象是抛物线,开口方向向上,故选项B错误;
故选:A.
【点评】本题考查了动点问题的函数图象,分段写出函数的解析式并数形结合进行分析是解题的关键.
13.【分析】利用相反数的定义求出,确定出m的值,代入原式计算即可得到结果.
解:根据题意得:,,
∴.
故答案为:1.
【点评】此题考查了相反数的定义,代数式求值,熟练掌握运算法则是解本题的关键.
14.【分析】根据平方根以及立方根的定义即可直接求解.
解:∵(±2)2=8,
∴8的平方根是:±2;
∵(-2)3=-8,
∴-8的立方根是:-2.
故答案是:±2,-2.
【点评】本题主要考查了立方根的概念的运用.如果一个数x的立方等于a,即x的三次方等于a(x3=a),那么这个数x就叫做a的立方根,也叫做三次方根.读作“三次根号a”其中,a叫做被开方数,3叫做根指数.
15.【分析】根据方位角的定义可得:,,进而即可求解.
解:如图所示:
由题意得:,,
∴,
∴=,
故答案为:63°.
【点评】本题主要考查方位角以及平行线的性质,熟练掌握两直线平行同旁内角互补是关键.
16.【分析】直接利用新定义分别计算与,再比较大小即可,分别按新定义计算,建立分式方程求解即可.
解:,
.
故答案为:.
,
经检验:是原方程的根,
故答案为:
【点评】本题考查了有理数的除法运算及有理数的大小比较,同时考查了分式方程的解法,掌握以上知识是解题的关键.
17.【分析】连接,根据等边△OAB,求出∠AOB,根据四边形是菱形,求出,得出△DEO为等边三角形,求出求出,过作于,求出,即可求出k.
解:连接,
是等边三角形,
四边形是菱形,
是等边三角形,
过作于,
反比例函数的图象经过点,
的值为,
故答案为 .
【点评】本题考查的是反比例函数,熟练掌握菱形,三角形的性质是解题的关键.
18.【分析】(1)先根据垂径定理确定圆心,连接,由勾股定理可求出的长;
(2)作直径的垂直平分线交半圆于,连接,则在以为圆心,为半径的圆上运动,当E,O,三点共线时, 最长
解:(1)如图,
,
故答案为:;
(2)如图,点,,即为所画,
作直径的垂直平分线交半圆于,连接则在以为圆心,为半径的圆上运动,直径的垂直平分线交于,过作的垂线交于,当E,O,三点共线时,最长,则点即为所求.
理由如下:
由作图可得:,
∴,
∴,
∴,
∴在以为圆心,为半径的圆上运动,是的垂直平分线,
∴,,
∴,
∴当E,O,三点共线时,最长,则点即为所求.
故答案为:作直径的垂直平分线交半圆于,连接则在以为圆心,为半径的圆上运动,直径的垂直平分线交于,过作的垂线交于,当E,O,三点共线时,最长,则点即为所求.
【点评】本题主要考查了圆心的确定,垂径定理的应用,勾股定理以及在网格中确定三角形外接圆圆心,正确作出图形是解答本题的关键.
19.【分析】(1)分别利用实数的运算法则和有理数的乘方运算法则计算求出答案;
(2)利用加减法消元求解即可.
解:(1)原式==5;
(2)
由②-①得:
把代入方程①,得
所以方程组的解为.
【点评】本题考查了解二元一次方程组,及实数的运算,熟练掌握运算法则是解题的关键.
20.【分析】先根据分式的混合运算化简,再将字母的值代入求解
解:原式,
当时,原式.
【点评】本题考查了分式的化简求值,实数的混合运算,正确的化简分式是解题的关键.
21.【分析】列表得出所有等可能结果,从中找到两个球颜色相同的结果数,利用概率公式就可算出.
解:列表如下
如图知,共有9种情况,
其中摸出的两个球颜色相同的由4种情况
所以摸出两个球颜色相同的概率为.
【点评】本题考查了列表法和树状图的知识,熟练运用列表和树状图列举出所有等可能是解题关键.
22.【分析】(1)①利用平行线分线段成比例定理即可解决问题;
②利用相似三角形的中面积比等于相似比的平方即可解决问题;
(2)利用平行四边形的性质可知OB=OD,BC∥AD,BC=AD,由题意可知BF:DF=n:(2m+n),即BE:AD=BF:DF=n:(2m+n),故求得=.
解:(1)①∵四边形ABCD是平行四边形,
∴BC=AD,BC∥AD,
∵BE:BC=1:3,
∴==.
②∵BE∥AD,
∴△BEF∽△DAF,
∴()2=.
(2)∵四边形ABCD是平行四边形,
∴OB=OD,BC∥AD,BC=AD,
∵BF:OF=n:m,
∴BF:DF=n:(2m+n),
∴BE:AD=BF:DF=n:(2m+n),
∴=.
【点评】本题考查相似三角形的判定和性质、平行四边形的性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.
23.【分析】(1)利用平行线性质和正方形的性质可得∠AEB=∠CFD,∠ABE=∠CDF,AB=CD,则借助AAS可证明△ABE≌△CDF;
(2)过点E作HE⊥BE,交AB于H点,证明∠HAE=∠HEA,得到AH=HE.设BE=DF=HE=AH=x,则HB=x.根据AB=4,构造关于x的方程,解方程即可.
解:(1)∵AE∥CF,
∴∠AEF=∠CFB.
∴∠AEB=∠CFD.
∵四边形ABCD是正方形,
∴∠ABE=∠CDF,AB=CD,
∴△ABE≌△CDF(AAS).
(2)过点E作HE⊥BE,交AB于H点,
∴∠BHE=∠HBE=45°.
∵∠ABE=2∠BAE,
∴∠BHE=2∠BAE.
又∵∠BHE=∠HAE+∠AEH,
∴∠HAE=∠HEA.
∴AH=HE.
设BE=DF=HE=AH=x,
则HB=
∴=4,解得x=4﹣4.
∴DF=4﹣4.
【点评】本题主要考查了正方形的性质、全等三角形的判定和性质,此题第一问简单,第二问是“倍半角”问题,通过辅助线构造等腰三角形转化角的解决这类问题的通用方法.
24.【分析】(1)根据脂肪所占的百分比结合这份快餐的总质量,即可求出结论;
(2)这份快餐所含蛋白质的质量为x克,则含矿物质的质量为x克,然后列方程求解即可;
(3)设这份快餐所含蛋白质的质量为y克,则含矿物质的质量为y克,含碳水化合物的质量为(400×85%﹣y)克,然后列方程求解即可.
解:(1)400×5%=20(克).
答:这份快餐中所含脂肪质量为20克.
(2)设这份快餐所含蛋白质的质量为x克,则含矿物质的质量为x克,
依题意得:x+20+x+400×40%=400,
解得:x=176.
答:这份快餐所含蛋白质的质量为176克.
(3)设这份快餐所含蛋白质的质量为y克,则含矿物质的质量为y克,含碳水化合物的质量为(400×85%﹣y)克,
依题意得:400×85%+20+y=400,
解得:y=160,
∴400×85%﹣y=340﹣160=180(克).
答:其中所含碳水化合物的质量为180克.
【点评】本题主要考查了一元一次方程的实际应用,解题的关键在于能够准确找到等量关系列出方程.
25.【分析】(1)由点P(x,y)在第二象限,推出x<0,y>0,根据sinα=,cosα=,tanα=,cotα=,即可判断;
(2)分两种情形讨论即可解决问题;
(3)如图2中,作PE⊥x轴于E.想办法求出OE的长,根据三角函数的定义即可解决问题;
(4)当α=0°或90°时,得到sinα+cosα的最小值sinα+cosα=1,当α=45°时,得到sinα+cosα的最大值,sinα+cosα=,由此即可解决问题.
解:(1)∵点P(x,y)在第二象限,
∴x<0,y>0,
∵sinα=,cosα=,tanα=,cotα=,
∴sinα>0,cosα<0,tanα<0,cotα<0,
∴取取正值的是sinα.
(2)如图1中,
①当点P在第一象限时,作PE⊥x轴于E.设OE=a,则PE=2a,OP=a,
∴sinα+cosα=.
②当点P在第三象限时,作PE⊥x轴于E.设OE=a,则PE=2a,OP=a,
∴sinα+cosα=.
综上所述,sinα+cosα=或.
(3)如图2中,作PE⊥x轴于E.
由题意PE=,cosα=,
∴OP=2,
∴OE=,
∴tanα=.
(4)当α=0°或90°时,得到sinα+cosα的最小值sinα+cosα=1,
当α=45°时,得到sinα+cosα的最大值,sinα+cosα=,
∴1≤sinα+cosα≤.
【点评】本题考查一次函数综合题、三角函数的定义、解直角三角形等知识,解题的关键是理解题意,学会用分类讨论的思想思考问题,学会利用参数解决问题,属于中考创新题目.
26.【分析】(1)设x=0,求出y的值,即可得到C的坐标,根据抛物线L3:得到抛物线的对称轴,由此可求出点C关于该抛物线对称轴对称的对称点D的坐标;
(2)由(1)可知点D的坐标为(4,1),再由条件以点D为顶点的L3的“友好”抛物线L4的解析式,可求出L4的解析式,进而可求出L3与L4中y同时随x增大而增大的自变量的取值范围;
(3)根据:抛物线L1的顶点A在抛物线L2上,抛物线L2的顶点B也在抛物线L1上,可以列出两个方程,相加可得(a1+a2)(h-m)2=0.可得.
解:(1)∵抛物线l3:,
∴顶点为(2,-1),对称轴为x=2,
设x=0,则y=1,
∴C(0,1),
∴点C关于该抛物线对称轴对称的对称点D的坐标为:(4,1);
(2)解:设的函数表达式为
由“友好”抛物线的定义,过点
的函数表达式为
与中同时随增大而增大的自变量的取值范围是
(3)
理由如下:
∵ 抛物线与抛物线互为“友好”抛物线,
①+②得:
【点评】本题属于二次函数的综合题,涉及了抛物线的对称变换、抛物线与坐标轴的交点坐标以及新定义的问题,解答本题的关键是数形结合,特别是(3)问根据已知条件得出方程组求解,有一定难度.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
【备考2023】广西玉林市中考数学模拟试卷2
姓名:__________班级:__________考号:__________总分__________
一、选择题(本大题共12小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的,把正确答案的标号填(涂)在答题卡内相应的位置上.)
1.中新网北京2021年4月2日电,截至4月2日15时,北京累计接种新冠疫苗人数累计接种新冠疫苗超16 000 000剂次.数据16 000 000可用科学记数法表示为( )
A.16×106 B.1.6×107 C.0.16×108 D.1.6×106
2.现有一组数据:2,3,3,4,4,5,6,则下列说法正确的是( )
A.众数是3 B.众数是4 C.中位数是3.5 D.中位数是4
3.一个几何体的俯视图如图所示,其中的数字表示该位置上小正方体的个数,那么这个几何体的主视图是( )
A. B. C. D.
4.在计算时,佳佳的板演过程如下:
解:原式.
老师问:“佳佳同学在解答过程中运用了哪些运算律?”
甲同学回答说:“佳佳在解答过程中运用了加法交换律”;
乙同学回答说:“佳佳在解答过程中运用了加法结合律”;
丙同学回答说:“佳佳在解答过程中既运用了加法交换律,也运用了加法结合律”.
下列对甲、乙、丙三名同学说法判断正确的是( )
A.甲同学说的对 B.乙同学说的对
C.丙同学说的对 D.甲、乙、丙说的都不对
5.下列计算正确的是( )
A. B.
C. D.
6.在Rt△ABC 中,∠C=90°,,AB=5cm,则AC的长度是( )
A.3 cm B.4 cm C.5 cm D.6 cm
7.下面事件是随机事件的是( )
A.掷一枚硬币,出现反面
B.在标准大气压下,水加热到8℃时会沸腾
C.实数的绝对值不小于零
D.如果a,b是实数,那么a b=b a
8.如图,的直径与弦交于点E,若B为的中点,则下列说法错误的是( ).
A. B. C. D.
9.已知x1,x2是一元二次方程x2﹣2x-3=0的两根,则x1+x2的值是( )
A.0 B.2 C.-2 D.4
10.如图,已知矩形,下列条件能使矩形成为正方形的是( )
A. B. C. D.
11.观察下列四个图形组成的一组图形,发现它们是按照一定规律排列的,依此规律排列下去,第10个图形共有( )个点组成
A.26 B.27 C.28 D.29
12.如图,在中,,,于点.点从点出发,沿的路径运动,运动到点停止,过点作于点,作于点.设点运动的路程为,四边形的面积为,则能反映与之间函数关系的图象是( )
A. B. C. D.
二、填空题(本大题共6小题,每小题3分,共18分.把答案填在答题卡中的横线上.)
13.若和互为相反数,是最大的负整数,则______.
14.计算:8的平方根______,-8的立方根是_____.
15.如图,A、、三岛平面图,岛在岛的北偏东80°方向,A岛在岛的北偏西37°方向,从C岛看A,两岛的视角度数为______.
16.对于任意非零实数、,规定,例如:,则______(填“”,或“”或“”)若,则______.
17.如图,在平面直角坐标系中,等边和菱形的边都在轴上,点在边上,,反比例函数的图象经过点,则的值为_____.
18.如图,在每个小正方形的边长为1的网格中,上的点,圆心均在格点上,
(1)_____________;
(2)若点是上的一个动点,连接,将绕点逆时针旋转得到,连,当线段最长时,点的对应点为点,点的对应点为点,请用无刻度的直尺,在如图所示的网格中,画出点,,并简要说明点,的位置是如何找到的(不要求证明)____________________.
三、解答题(本大题共8小题,满分共66分.解答应写出证明过程或演算步骤(含相应的文字说明).将解答写在答题卡上)
19.计算:(1)
(2)解方程组.
20.先化简,后求值:;其中.
21.现有两个不透明的袋子,一个装有2个红球,1个白球,一个装有1个黄球,2个红球,这些球除颜色外完全相同,从两个袋子中各随机摸出一个球,利用树状图或列表的方法,求摸出的两个球颜色相同的概率.
22.如图,在平行四边形ABCD中,AC,BD相交于点O,点E在BC上,AE交BD于F.
(1)若E是靠近点B的三等分点,求;①的值;②△BEF与△DAF的面积比;
(2)当时,求的值.
23.如图,已知正方形ABCD中,AB=4,点E,F在对角线BD上,AE∥CF.
(1)求证:△ABE≌△CDF;
(2)若∠ABE=2∠BAE,求DF的长.
24.2012年5月20日是第23个中国学生营养日,某校社会实践小组开展活动,调查快餐营养情况,他们从食品安全监督部门获取了一份快餐的信息.根据信息,解答下列问题.
信息:
1.快餐的成分:蛋白质、脂肪、矿物质、碳水化合物;
2.快餐总质量为400克;
3.脂肪所占的百分比为5%;
4.所含蛋白质质量是矿物质质量的4倍.
(1)求这份快餐中所含脂肪质量;
(2)若碳水化合物占快餐总质量的40%,求这份快餐所含蛋白质的质量;
(3)若这份快餐中蛋白质和碳水化合物所占百分比的和是85%,求其中所含碳水化合物的质量.
25.阅读下面材料,完成后面题目.
0°-360°间的角的三角函数
在初中,我们学习过锐角的正弦、余弦、正切和余切四种三角函数,即在图1所示的直角三角形ABC,∠A是锐角,那么sinA=,cosA=,tanA=,cotA=
为了研究需要,我们再从另一个角度来规定一个角的三角函数的意义:
设有一个角α,我们以它的顶点作为原点,以它的始边作为x轴的正半轴ox,建立直角坐标系(图2),在角α的终边上任取一点P,它的横坐标是x,纵坐标是y,点P和原点(0,0)的距离为r=(r总是正的),然后把角α的三角函数规定为:sinα=,cosα=,tanα=,cotα=
我们知道,图1的四个比值的大小与角A的大小有关,而与直角三角形的大小无关,同样图2中四个比值的大小也仅与角α的大小有关,而与点P在角α的终边位置无关.
比较图1与图2,可以看出一个角的三角函数的意义的两种规定实际上是一样的,根据第二种定义回答下列问题.
(1)若90°<α<180°,则角α的三角函数值sinα、cosα、tanα、cotα,其中取正值的是哪几个?
(2)若角α的终边与直线y=2x重合,求sinα+cosα的值.
(3)若角α是钝角,其终边上一点P(x,),且cosα=x,求tanα的值.
(4)若0°≤α≤90°,求sinα+cosα的取值范围.
26.(如图 1,若抛物线 l1的顶点 A 在抛物线 l2上,抛物线 l2的顶点 B 也在抛物线 l1上(点 A 与点 B 不重合).我们称抛物线 l1,l2互为“友好”抛物线,一条抛物线的“友 好”抛物线可以有多条.
(1)如图2,抛物线 l3: 与y 轴交于点C,点D与点C关于抛物线的对称轴对称,则点 D 的坐标为 ;
(2)求以点 D 为顶点的 l3的“友好”抛物线 l4的表达式,并指出 l3与 l4中y 同时随x增大而增大的自变量的取值范围;
(3)若抛物线 y=a1(x-m)2+n 的任意一条“友好”抛物线的表达式为 y=a2(x-h)2+k, 写出 a1与a2的关系式,并说明理由.
参考答案:
1.【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.
解:将16 000 000用科学记数法表示为1.6×107.
故选:B.
【点评】本题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.
2.【分析】根据求出这组数据的众数和中位数即可求解.
解:数据2,3,3,4,4,5,6的众数是3和4,中位数是4.
故选:D
【点评】本题考查了求一组数据的众数和中位数,众数是指一组数据中出现次数最多的数,中位数是指将数据排序后处于中间位置是数,熟知众数和中位数的意义是解题关键.
3.【分析】一一对应即可.
解:最左边有一个,中间有两个,最右边有三个,所以选A.
【点评】理解立体几何的概念是解题的关键.
4.【分析】根据加法运算律的定义进行解答即可.
解:由到既运用了加法交换律,也运用了加法结合律,所以丙同学说的对,故C正确.
故选:C.
【点评】本题主要考查了加法的交换律和结合律,熟记加法交换律和结合律,,,是解题的关键.
5.【分析】根据合并同类项的方法逐项计算即可.
解:A.a与b不是同类项,不能合并,故不正确;
B.,故不正确;
C.,故不正确;
D.,正确;
故选D.
【点评】本题考查了同类项的定义及合并同类项,熟练掌握合并同类项的方法是解答本题的关键.所含字母相同,并且相同字母的指数也相同的项,叫做同类项;合并同类项时,把同类项的系数相加,所得和作为合并后的系数,字母和字母的指数不变.
6.【分析】根据三角函数的定义求得BC和AB的比值,设出BC、AB,然后利用勾股定理计算即可;
解:∵,
∴设,,
又∵AB=5cm,
∴,
∴,
∴,
∴;
故选B.
【点评】本题主要考查了锐角三角函数与勾股定理,准确计算是解题的关键.
7.【分析】直接利用随机事件以及不可能事件和必然事件的定义分析得出答案.
解:A、掷一枚硬币,出现反面,是随机事件,符合题意;
B、在标准大气压下,水加热到8℃时会沸腾,是不可能事件,不合题意;
C、实数的绝对值不小于零,是必然事件,不合题意;
D、如果a,b是实数,那么a b=b a,是必然事件,不合题意;
故选:A.
【点评】本题考查随机事件的判断,是基础题,解题时要认真审题,注意随机事件的定义的合理运用.
8.【分析】根据垂径定理对各选项进行逐一分析即可.
解:∵的直径与弦交于点E, B为的中点,
∴,,故A,C,D选项正确,
不能得出,故B选项不正确,
故选:B.
【点评】本题考查的是垂径定理的推理,掌握垂径定理是解题的关键.一条直线如果具有①经过圆心,②垂直于弦,③平分弦(被平分的弦不是直径),④平分弦所对的优弧,⑤平分弦所对的劣弧这五条中的任意两条,则必然具备其余的三条,简称“知二推三”.
9.【分析】直接根据根与系数的关系进行求解,即可得到答案.
解:∵x1,x2是一元二次方程x2﹣2x3=0的两根,
∴,
故选:B.
【点评】本题考查了一元二次方程的根与系数的关系,解题的关键是掌握根与系数的关系进行解题.
10.【分析】已知四边形是矩形,要使它成为正方形只有两种方法:(1)一组邻边相等;(2)对角线互相垂直,据此求解即可.
解:∵四边形是矩形,
∴当或当或或或时,四边形是正方形;
故选:B.
【点评】本题主要考查了正方形的判定,熟练地掌握正方形的判定方法是解题的关键.(1)一组邻边相等的矩形是正方形;(2)对角线互相垂直的矩形是正方形.
11.【分析】观察图形,在1个点的基础上,依次多3个;根据其中的规律,用字母表示即可,再把字母的值为10代入计算即可.
解:∵第1个图形为1个点,
第2个图形为1+3=4个点,
第3个图形为1+3+3=7个点,
第3个图形为1+3+3=7个点,
第4个图形为1+3+3+3=10个点,
……,
∴第n个图形为1+3=个点,
当时,
故选C
【点评】本题主要考查学生对图形的变化类的知识点的理解和掌握,此题的关键是注意发现前后图形中的数量之间的关系.
12.【分析】分两段来分析:①点P从点A出发运动到点D时,写出此段的函数解析式,则可排除C和D;②P点过了D点向C点运动,作出图形,写出此阶段的函数解析式,根据图象的开口方向可得答案.
解:∵,,
∴,,
又∵,
∴,,
∵,,
∴四边形是矩形,
I.当P在线段AD上时,即时,如解图1
∴,
∴,
∴四边形的面积为,此阶段函数图象是抛物线,开口方向向下,故选项CD错误;
II.当P在线段CD上时,即时,如解图2:
依题意得:,
∵,,
∴,
∴,
∴四边形的面积为,此阶段函数图象是抛物线,开口方向向上,故选项B错误;
故选:A.
【点评】本题考查了动点问题的函数图象,分段写出函数的解析式并数形结合进行分析是解题的关键.
13.【分析】利用相反数的定义求出,确定出m的值,代入原式计算即可得到结果.
解:根据题意得:,,
∴.
故答案为:1.
【点评】此题考查了相反数的定义,代数式求值,熟练掌握运算法则是解本题的关键.
14.【分析】根据平方根以及立方根的定义即可直接求解.
解:∵(±2)2=8,
∴8的平方根是:±2;
∵(-2)3=-8,
∴-8的立方根是:-2.
故答案是:±2,-2.
【点评】本题主要考查了立方根的概念的运用.如果一个数x的立方等于a,即x的三次方等于a(x3=a),那么这个数x就叫做a的立方根,也叫做三次方根.读作“三次根号a”其中,a叫做被开方数,3叫做根指数.
15.【分析】根据方位角的定义可得:,,进而即可求解.
解:如图所示:
由题意得:,,
∴,
∴=,
故答案为:63°.
【点评】本题主要考查方位角以及平行线的性质,熟练掌握两直线平行同旁内角互补是关键.
16.【分析】直接利用新定义分别计算与,再比较大小即可,分别按新定义计算,建立分式方程求解即可.
解:,
.
故答案为:.
,
经检验:是原方程的根,
故答案为:
【点评】本题考查了有理数的除法运算及有理数的大小比较,同时考查了分式方程的解法,掌握以上知识是解题的关键.
17.【分析】连接,根据等边△OAB,求出∠AOB,根据四边形是菱形,求出,得出△DEO为等边三角形,求出求出,过作于,求出,即可求出k.
解:连接,
是等边三角形,
四边形是菱形,
是等边三角形,
过作于,
反比例函数的图象经过点,
的值为,
故答案为 .
【点评】本题考查的是反比例函数,熟练掌握菱形,三角形的性质是解题的关键.
18.【分析】(1)先根据垂径定理确定圆心,连接,由勾股定理可求出的长;
(2)作直径的垂直平分线交半圆于,连接,则在以为圆心,为半径的圆上运动,当E,O,三点共线时, 最长
解:(1)如图,
,
故答案为:;
(2)如图,点,,即为所画,
作直径的垂直平分线交半圆于,连接则在以为圆心,为半径的圆上运动,直径的垂直平分线交于,过作的垂线交于,当E,O,三点共线时,最长,则点即为所求.
理由如下:
由作图可得:,
∴,
∴,
∴,
∴在以为圆心,为半径的圆上运动,是的垂直平分线,
∴,,
∴,
∴当E,O,三点共线时,最长,则点即为所求.
故答案为:作直径的垂直平分线交半圆于,连接则在以为圆心,为半径的圆上运动,直径的垂直平分线交于,过作的垂线交于,当E,O,三点共线时,最长,则点即为所求.
【点评】本题主要考查了圆心的确定,垂径定理的应用,勾股定理以及在网格中确定三角形外接圆圆心,正确作出图形是解答本题的关键.
19.【分析】(1)分别利用实数的运算法则和有理数的乘方运算法则计算求出答案;
(2)利用加减法消元求解即可.
解:(1)原式==5;
(2)
由②-①得:
把代入方程①,得
所以方程组的解为.
【点评】本题考查了解二元一次方程组,及实数的运算,熟练掌握运算法则是解题的关键.
20.【分析】先根据分式的混合运算化简,再将字母的值代入求解
解:原式,
当时,原式.
【点评】本题考查了分式的化简求值,实数的混合运算,正确的化简分式是解题的关键.
21.【分析】列表得出所有等可能结果,从中找到两个球颜色相同的结果数,利用概率公式就可算出.
解:列表如下
如图知,共有9种情况,
其中摸出的两个球颜色相同的由4种情况
所以摸出两个球颜色相同的概率为.
【点评】本题考查了列表法和树状图的知识,熟练运用列表和树状图列举出所有等可能是解题关键.
22.【分析】(1)①利用平行线分线段成比例定理即可解决问题;
②利用相似三角形的中面积比等于相似比的平方即可解决问题;
(2)利用平行四边形的性质可知OB=OD,BC∥AD,BC=AD,由题意可知BF:DF=n:(2m+n),即BE:AD=BF:DF=n:(2m+n),故求得=.
解:(1)①∵四边形ABCD是平行四边形,
∴BC=AD,BC∥AD,
∵BE:BC=1:3,
∴==.
②∵BE∥AD,
∴△BEF∽△DAF,
∴()2=.
(2)∵四边形ABCD是平行四边形,
∴OB=OD,BC∥AD,BC=AD,
∵BF:OF=n:m,
∴BF:DF=n:(2m+n),
∴BE:AD=BF:DF=n:(2m+n),
∴=.
【点评】本题考查相似三角形的判定和性质、平行四边形的性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.
23.【分析】(1)利用平行线性质和正方形的性质可得∠AEB=∠CFD,∠ABE=∠CDF,AB=CD,则借助AAS可证明△ABE≌△CDF;
(2)过点E作HE⊥BE,交AB于H点,证明∠HAE=∠HEA,得到AH=HE.设BE=DF=HE=AH=x,则HB=x.根据AB=4,构造关于x的方程,解方程即可.
解:(1)∵AE∥CF,
∴∠AEF=∠CFB.
∴∠AEB=∠CFD.
∵四边形ABCD是正方形,
∴∠ABE=∠CDF,AB=CD,
∴△ABE≌△CDF(AAS).
(2)过点E作HE⊥BE,交AB于H点,
∴∠BHE=∠HBE=45°.
∵∠ABE=2∠BAE,
∴∠BHE=2∠BAE.
又∵∠BHE=∠HAE+∠AEH,
∴∠HAE=∠HEA.
∴AH=HE.
设BE=DF=HE=AH=x,
则HB=
∴=4,解得x=4﹣4.
∴DF=4﹣4.
【点评】本题主要考查了正方形的性质、全等三角形的判定和性质,此题第一问简单,第二问是“倍半角”问题,通过辅助线构造等腰三角形转化角的解决这类问题的通用方法.
24.【分析】(1)根据脂肪所占的百分比结合这份快餐的总质量,即可求出结论;
(2)这份快餐所含蛋白质的质量为x克,则含矿物质的质量为x克,然后列方程求解即可;
(3)设这份快餐所含蛋白质的质量为y克,则含矿物质的质量为y克,含碳水化合物的质量为(400×85%﹣y)克,然后列方程求解即可.
解:(1)400×5%=20(克).
答:这份快餐中所含脂肪质量为20克.
(2)设这份快餐所含蛋白质的质量为x克,则含矿物质的质量为x克,
依题意得:x+20+x+400×40%=400,
解得:x=176.
答:这份快餐所含蛋白质的质量为176克.
(3)设这份快餐所含蛋白质的质量为y克,则含矿物质的质量为y克,含碳水化合物的质量为(400×85%﹣y)克,
依题意得:400×85%+20+y=400,
解得:y=160,
∴400×85%﹣y=340﹣160=180(克).
答:其中所含碳水化合物的质量为180克.
【点评】本题主要考查了一元一次方程的实际应用,解题的关键在于能够准确找到等量关系列出方程.
25.【分析】(1)由点P(x,y)在第二象限,推出x<0,y>0,根据sinα=,cosα=,tanα=,cotα=,即可判断;
(2)分两种情形讨论即可解决问题;
(3)如图2中,作PE⊥x轴于E.想办法求出OE的长,根据三角函数的定义即可解决问题;
(4)当α=0°或90°时,得到sinα+cosα的最小值sinα+cosα=1,当α=45°时,得到sinα+cosα的最大值,sinα+cosα=,由此即可解决问题.
解:(1)∵点P(x,y)在第二象限,
∴x<0,y>0,
∵sinα=,cosα=,tanα=,cotα=,
∴sinα>0,cosα<0,tanα<0,cotα<0,
∴取取正值的是sinα.
(2)如图1中,
①当点P在第一象限时,作PE⊥x轴于E.设OE=a,则PE=2a,OP=a,
∴sinα+cosα=.
②当点P在第三象限时,作PE⊥x轴于E.设OE=a,则PE=2a,OP=a,
∴sinα+cosα=.
综上所述,sinα+cosα=或.
(3)如图2中,作PE⊥x轴于E.
由题意PE=,cosα=,
∴OP=2,
∴OE=,
∴tanα=.
(4)当α=0°或90°时,得到sinα+cosα的最小值sinα+cosα=1,
当α=45°时,得到sinα+cosα的最大值,sinα+cosα=,
∴1≤sinα+cosα≤.
【点评】本题考查一次函数综合题、三角函数的定义、解直角三角形等知识,解题的关键是理解题意,学会用分类讨论的思想思考问题,学会利用参数解决问题,属于中考创新题目.
26.【分析】(1)设x=0,求出y的值,即可得到C的坐标,根据抛物线L3:得到抛物线的对称轴,由此可求出点C关于该抛物线对称轴对称的对称点D的坐标;
(2)由(1)可知点D的坐标为(4,1),再由条件以点D为顶点的L3的“友好”抛物线L4的解析式,可求出L4的解析式,进而可求出L3与L4中y同时随x增大而增大的自变量的取值范围;
(3)根据:抛物线L1的顶点A在抛物线L2上,抛物线L2的顶点B也在抛物线L1上,可以列出两个方程,相加可得(a1+a2)(h-m)2=0.可得.
解:(1)∵抛物线l3:,
∴顶点为(2,-1),对称轴为x=2,
设x=0,则y=1,
∴C(0,1),
∴点C关于该抛物线对称轴对称的对称点D的坐标为:(4,1);
(2)解:设的函数表达式为
由“友好”抛物线的定义,过点
的函数表达式为
与中同时随增大而增大的自变量的取值范围是
(3)
理由如下:
∵ 抛物线与抛物线互为“友好”抛物线,
①+②得:
【点评】本题属于二次函数的综合题,涉及了抛物线的对称变换、抛物线与坐标轴的交点坐标以及新定义的问题,解答本题的关键是数形结合,特别是(3)问根据已知条件得出方程组求解,有一定难度.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
