第十二章 证明 章末复习课件(29张PPT)
文档属性
| 名称 | 第十二章 证明 章末复习课件(29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-10 00:00:00 | ||
图片预览







文档简介
(共29张PPT)
第十二章 · 证 明
小结与思考
1. 了解定义、命题、定理、逆命题、互逆命题等概念;
2.会区分命题的条件和结论.会判断一个命题的真假.会写出一个命题的逆命题,并知道如果一个命题是真命题,它的逆命题不一定是真命题;
3.通过具体的例子理解反例的作用;
4. 理解证明的必要性,掌握证明的格式.
学习目标
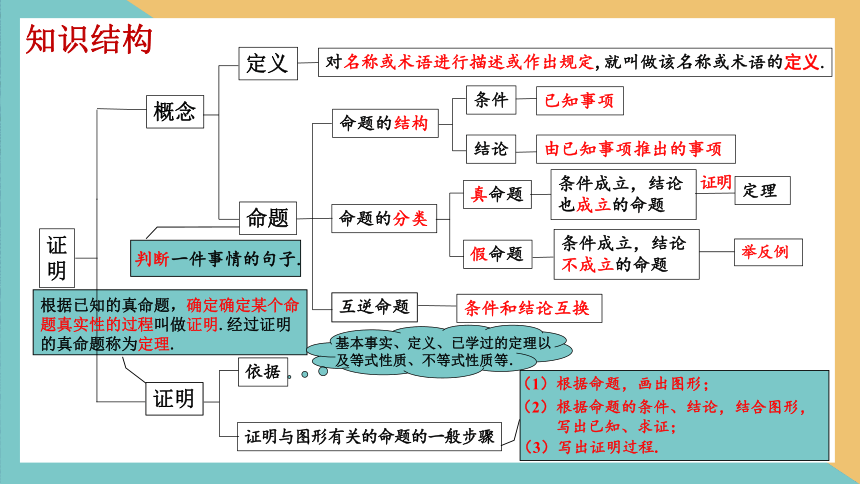
知识结构
证明
概念
证明
互逆命题
定义
命题
对名称或术语进行描述或作出规定,就叫做该名称或术语的定义.
命题的结构
命题的分类
条件
结论
真命题
假命题
已知事项
由已知事项推出的事项
判断一件事情的句子.
条件成立,结论也成立的命题
条件成立,结论不成立的命题
条件和结论互换
证明
定理
举反例
依据
证明与图形有关的命题的一般步骤
(1)根据命题,画出图形;
(2)根据命题的条件、结论,结合图形,
写出已知、求证;
(3)写出证明过程.
基本事实、定义、已学过的定理以及等式性质、不等式性质等.
根据已知的真命题,确定确定某个命题真实性的过程叫做证明.经过证明的真命题称为定理.
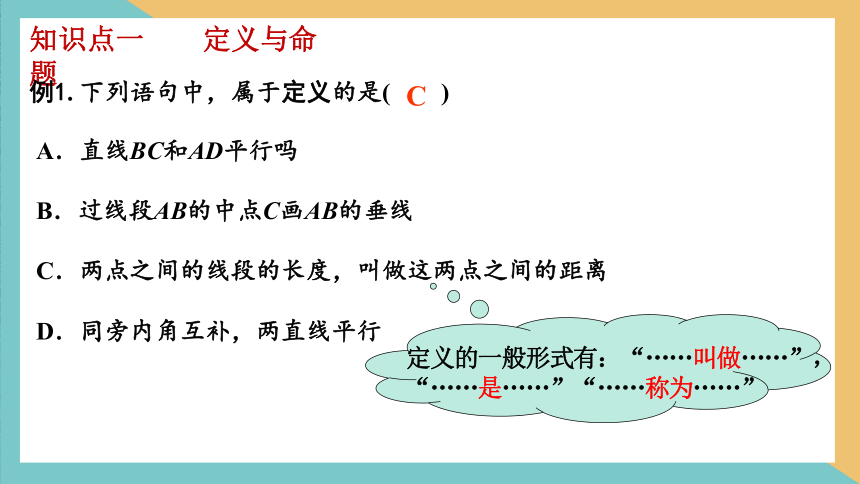
知识点一 定义与命题
例1. 下列语句中,属于定义的是( )
A.直线BC和AD平行吗
B.过线段AB的中点C画AB的垂线
C.两点之间的线段的长度,叫做这两点之间的距离
D.同旁内角互补,两直线平行
C
定义的一般形式有:“……叫做……”,“……是……”“……称为……”
知识点一 定义与命题
例2. 下列语句中,属于命题的是( )
A.同角的余角相等
B.过点A作直线MN
C.∠1=∠2吗
D.取线段AB的中点
A
命题的特征:是句子、有判断(只需作出判断、无关对错.)
注意:疑问句、祈使句、命令句、感叹句等不是命题.
知识点一 定义与命题
例3. 命题“垂直于同一条直线的两条直线互相平行”的条件是( )
A.垂直
B.两条直线
C.同一条直线
D.两条直线垂直于同一条直线
改写:如果两条直线垂直于同一条直线,那么这两条直线互相平行.
有些时候,我们可以通过将命题改写成
“如果······那么······ ”的形式,找出命题的条件和结论.
D
知识点一 定义与命题
例4. 下列命题中,属于假命题的是( )
A.对顶角相等
B.同位角相等
C.两点确定一条直线
D.n边形(n≥3)的内角和是(180n-360)°
判断一个命题是假命题只需举出一个反例.使之具有命题的条件,而不具有命题的结论.
B
1
2
知识点一 定义与命题
例5. 说出下列命题的逆命题,并判定原命题和逆命题的真假:
( )
( )
( )
( )
(1)轴对称图形是等腰三角形;
逆命题:等腰三角形是轴对称图形.
假命题
真命题
(2)同角的补角相等.
逆命题:如果两个角相等,那么这两个角是同一个角的补角.
真命题
假命题
把一个命题的条件和结论互换就得到它的逆命题,每个命题都有逆命题.原命题是真命题,它的逆命题不一定是真命题.
巩固练习
1. 下列命题中,属于真命题的是( )
D
A.内错角相等
B.若a10=b10,则a=b
C.任意多边形的内角和为360°
D.等角的补角相等
2. 能说明命题“对于任何数a,|a|>-a”是假命题的一个反例可以是( )
A
A. a=-π B. a= C. a=1 D.3.1415962…
巩固练习
3. “两负数的商为正数”的条件是___________,结论是_____________ ;
4. 改写命题“等角的补角相等”:如果_________,那么_______________.
5. 命题: 如果,那么a>b.
(1) 这个命题的逆命题是真命题吗?说明你的理由.
(2) 如果(1)中的逆命题不是真命题,请你添加一个条件使之成为真命题,写出这个真命题.
两个数为负数
它们的商为正数
两个角相等
这两个角的补角相等
解:(1)不是真命题. 反例:a=1,b=-2时,a>b,那么| |<| |
解:(2) 如果a>b且a、b是非负数,那么| |>| |.
知识点二 证明
有关定理
(5)平行于同一条直线的两条直线平行.
(3)直角三角形的两个锐角互余.
(4)有两个角互余的三角形是直角三角形.
(2)三角形的外角等于与它不相邻的两个内角的和.
(1)三角形三个内角的和等于180°.
(一)证明的必要性
例6. 探索两个连续奇数的平方差的规律,并加以证明.
设n为整数,两个连续奇数分别为2n-1、2n+1,
∵(2n+1)2-(2n-1)2
=[(2n+1)+(2n-1)] [(2n+1)-(2n-1)]
=8n
解:两个连续奇数的平方差能被8整除.
∴两个连续奇数的平方差能被8整除.
例7. 证明:两直线平行,同旁内角互补.
(二)证明与图形有关的命题的一般步骤
(1)根据命题,画出图形;
F
2
3
1
A
B
C
D
E
(2)根据命题的条件、结论,结合图形,
写出已知、求证;
已知:AB∥CD;
求证:∠1 + ∠2 = 180°;
(3)写出证明过程.
证明:∵ AB∥CD(已知),
∴ ∠2=∠3(两直线平行,同位角相等),
∵ ∠1+∠3=180°(平角的定义),
∴ ∠1+∠2=180°(等量代换).
例8. 已知:AB∥CD,求证:∠A+∠C+∠AEC=360°.
F
)
1
)
2
证明:过E点作EF∥AB,
则∠A+∠1=180°(两直线平行平行,同旁内角互补)
∵AB∥CD(已知)
∴EF∥CD(平行于同一直线的两直线互相平行)
∴∠2+∠C=180°(两直线平行平行,同旁内角互补)
∴∠A+∠1+∠2+∠C=360°(等式的基本性质)
即∠A+∠C+∠AEC=360°
A
B
C
D
E
)
1
2
)
A
B
C
D
E
“铅笔头”模型
A
B
C
D
E
F
(三)与平行线的判定与性质相关的证明
变式1: 如图,AB∥CD,试用不同的方法证明∠AEC=∠A+∠C.
E
D
C
B
A
1
2
(
(
E
D
C
B
A
F
1
2
(
(
“猪蹄”模型
E
D
C
B
A
F
(三)与平行线的判定与性质相关的证明
(三)与平行线的判定与性质相关的证明
E
D
C
B
A
变式2: 如图,AB∥CD, ∠AEC与∠A、∠C 之间有怎样的数量关系?证明你的结论.
F
∠AEC=∠A-∠C
(三)与平行线的判定与性质相关的证明
变式3: 如图甲:已知AB∥DE,那么∠1+∠2+∠3等于多少度 试加以说明.
当已知条件不变,而图形变为如图乙时,结论改变了吗
图丙中的∠1+∠2+∠3+∠4是多少度呢?如果如丁图所示,∠1+∠2+∠3+…+∠n的和又为多少度?你找到了什么规律吗?
甲
乙
丙
丁
∠1+∠2+∠3=2×180°
∠1+∠2+∠3+∠4=3×180°
∠1+∠2+∠3+∠4+……+∠n=(n-1)×180°
E
D
C
B
A
B
A
D
C
E
F
(四)与三角形内角和定理相关的证明
例9: 将例8变式1的图中直线AB绕点A顺时针方向旋转一定角度交直线CD于点Q ,如下图,则∠AEC 、 ∠A、 ∠C、∠AFC 之间有何数量关系?
∠AEC= ∠A+∠C+∠AFC
“箭头”模型
P
变式1:在五角星ABCDE中,∠A、∠B、∠C、∠D、∠E的和等于多少度?请加以证明.
A
C
D
E
B
2
1
╮
╰
解:易证 ∠1+∠2=∠B+∠E
∵在△ACD中,
∠ A+∠ACD+∠ADC =180°
∴∠A+∠ACE+∠1+∠2+∠ADB=180°
即:∠A+ ∠B+ ∠C+ ∠D+ ∠E=180°
你还能想到其他证明方法吗?试一试 .
(四)与三角形内角和定理相关的证明
“8字”模型
变式2:把图1、图2叫蜕化的五角星,问它们的五角之和与五角星图形的五角之和仍相等吗?为什么?
(四)与三角形内角和定理相关的证明
D
A
E
C
(图1)
B
D
A
E
B
C
(图2)
相等
(四)与三角形内角和定理相关的证明
变式3:如图:求∠A+ ∠B+ ∠C+ ∠D+ ∠E+∠F的度数.
A
B
C
D
E
F
∠A+ ∠B+ ∠C+ ∠D+ ∠E+∠F=360°
巩固练习
1.下列关于判断一个数学结论是否正确的叙述中,正确的是( )
D
A. 只需观察得出
B. 只需依靠经验获得
C. 通过实验得出
D. 必须进行有根据的推理
2.下列平行线的判定方法中,是基本事实的是( )
A.同旁内角互补,两直线平行
B.同位角相等,两直线平行
C.内错角相等,两直线平行
D.在同一平面内,不相交的两条直线叫做平行线
B
3.如图,OP∥QR∥ST,则下列各式中正确的是( ).
A.∠1+∠2+∠3=180°
B.∠1+∠2-∠3=90°
C.∠1-∠2+∠3=90°
D.∠2+∠3-∠1=180°
D
Q
T
S
P
R
O
)
2
1
4
3
)
)
)
巩固练习
巩固练习
4. 如图,AB∥CD,EF⊥CD于点F.若∠BEF=150°,则∠ABE的度数为 60° .
60°
A
B
D
C
E
F
∟
巩固练习
5. 将一副三角尺按如图所示的方式摆放,且AB∥CD,则∠1的度数为 105 .
105°
A
B
C
1
∟
∟
D
巩固练习
6. 如图所示为可调躺椅示意图,AE与BD的交点为C,且∠A、∠B、∠E保持不变.为了舒适,需调整∠D的大小,使∠EFD=110°,则图中∠D应 减少 (填“增加”或“减少”) 10° .
减少
10°
C
B
A
D
E
F
50°
60°
20°
30°
巩固练习
7. 如图,AB∥DE,且∠1=∠2,∠3=∠4.求证:BC∥EF.
(1) 证明:∵ AB∥DE(已知),
∴ ∠1=∠3( 两直线平行,同位角相等 ).
∵ ∠1=∠2,∠3=∠4(已知),
∴ ∠2= ∠4 (等量代换).
∴ BC∥EF( 同位角相等,两直线平行 ).
(2) 上述推理过程中,运用的互逆的真命题是 “两直线平行,同位角相等”和“同位角相等,两直线平______ .
两直线平行,同位角相等
∠4
同位角相等,两直线平行
“两直线平行,同位角相等”
和“同位角相等,两直线平行”
A
B
C
D
E
2
F
1
3
4
8. 已知:如图,EF∥AD,∠1=∠2,∠BAC=70°.求∠AGD.
A
B
C
D
E
G
1
F
2
解:∵EF∥AD(已知),
∴∠2=∠3(两直线平行,同位角相等).
∵∠1=∠2(已知),
∴∠1=∠3(等量代换),
∴DG∥AB(内错角相等,两直线平行).
∴ ∠BAC+ ∠AGD=180°
(两直线平行,同旁内角互补)
∵∠BAC=70° (已知) ,
∴ ∠AGD=110° (等式性质) .
巩固练习
3
巩固练习
9.如图,在△ABC中,∠ACB=90°,AE是角平分线,CD是高,AE、CD相交于点F.
求证: ∠CFE= ∠CEF
C
∟
∟
A
B
D
E
F
证明:在△ACE、 △ADF中,
∵∠ACB=∠ADF=90°(已知),
∴∠CAE+ ∠CEF=90° 、∠DAF+ ∠AFD=90°
(直角三角形的两个锐角互余).
∵AE是角平分线(已知) ,
∴ ∠ CAE =∠ DAF (角平分线定义)
∴ ∠CEF = ∠ AFD(等式性质) .
∵ ∠CFE = ∠ AFD(对顶角相等) ,
∴ ∠CFE= ∠CEF (等量代换) .
第十二章 · 证 明
小结与思考
1. 了解定义、命题、定理、逆命题、互逆命题等概念;
2.会区分命题的条件和结论.会判断一个命题的真假.会写出一个命题的逆命题,并知道如果一个命题是真命题,它的逆命题不一定是真命题;
3.通过具体的例子理解反例的作用;
4. 理解证明的必要性,掌握证明的格式.
学习目标
知识结构
证明
概念
证明
互逆命题
定义
命题
对名称或术语进行描述或作出规定,就叫做该名称或术语的定义.
命题的结构
命题的分类
条件
结论
真命题
假命题
已知事项
由已知事项推出的事项
判断一件事情的句子.
条件成立,结论也成立的命题
条件成立,结论不成立的命题
条件和结论互换
证明
定理
举反例
依据
证明与图形有关的命题的一般步骤
(1)根据命题,画出图形;
(2)根据命题的条件、结论,结合图形,
写出已知、求证;
(3)写出证明过程.
基本事实、定义、已学过的定理以及等式性质、不等式性质等.
根据已知的真命题,确定确定某个命题真实性的过程叫做证明.经过证明的真命题称为定理.
知识点一 定义与命题
例1. 下列语句中,属于定义的是( )
A.直线BC和AD平行吗
B.过线段AB的中点C画AB的垂线
C.两点之间的线段的长度,叫做这两点之间的距离
D.同旁内角互补,两直线平行
C
定义的一般形式有:“……叫做……”,“……是……”“……称为……”
知识点一 定义与命题
例2. 下列语句中,属于命题的是( )
A.同角的余角相等
B.过点A作直线MN
C.∠1=∠2吗
D.取线段AB的中点
A
命题的特征:是句子、有判断(只需作出判断、无关对错.)
注意:疑问句、祈使句、命令句、感叹句等不是命题.
知识点一 定义与命题
例3. 命题“垂直于同一条直线的两条直线互相平行”的条件是( )
A.垂直
B.两条直线
C.同一条直线
D.两条直线垂直于同一条直线
改写:如果两条直线垂直于同一条直线,那么这两条直线互相平行.
有些时候,我们可以通过将命题改写成
“如果······那么······ ”的形式,找出命题的条件和结论.
D
知识点一 定义与命题
例4. 下列命题中,属于假命题的是( )
A.对顶角相等
B.同位角相等
C.两点确定一条直线
D.n边形(n≥3)的内角和是(180n-360)°
判断一个命题是假命题只需举出一个反例.使之具有命题的条件,而不具有命题的结论.
B
1
2
知识点一 定义与命题
例5. 说出下列命题的逆命题,并判定原命题和逆命题的真假:
( )
( )
( )
( )
(1)轴对称图形是等腰三角形;
逆命题:等腰三角形是轴对称图形.
假命题
真命题
(2)同角的补角相等.
逆命题:如果两个角相等,那么这两个角是同一个角的补角.
真命题
假命题
把一个命题的条件和结论互换就得到它的逆命题,每个命题都有逆命题.原命题是真命题,它的逆命题不一定是真命题.
巩固练习
1. 下列命题中,属于真命题的是( )
D
A.内错角相等
B.若a10=b10,则a=b
C.任意多边形的内角和为360°
D.等角的补角相等
2. 能说明命题“对于任何数a,|a|>-a”是假命题的一个反例可以是( )
A
A. a=-π B. a= C. a=1 D.3.1415962…
巩固练习
3. “两负数的商为正数”的条件是___________,结论是_____________ ;
4. 改写命题“等角的补角相等”:如果_________,那么_______________.
5. 命题: 如果,那么a>b.
(1) 这个命题的逆命题是真命题吗?说明你的理由.
(2) 如果(1)中的逆命题不是真命题,请你添加一个条件使之成为真命题,写出这个真命题.
两个数为负数
它们的商为正数
两个角相等
这两个角的补角相等
解:(1)不是真命题. 反例:a=1,b=-2时,a>b,那么| |<| |
解:(2) 如果a>b且a、b是非负数,那么| |>| |.
知识点二 证明
有关定理
(5)平行于同一条直线的两条直线平行.
(3)直角三角形的两个锐角互余.
(4)有两个角互余的三角形是直角三角形.
(2)三角形的外角等于与它不相邻的两个内角的和.
(1)三角形三个内角的和等于180°.
(一)证明的必要性
例6. 探索两个连续奇数的平方差的规律,并加以证明.
设n为整数,两个连续奇数分别为2n-1、2n+1,
∵(2n+1)2-(2n-1)2
=[(2n+1)+(2n-1)] [(2n+1)-(2n-1)]
=8n
解:两个连续奇数的平方差能被8整除.
∴两个连续奇数的平方差能被8整除.
例7. 证明:两直线平行,同旁内角互补.
(二)证明与图形有关的命题的一般步骤
(1)根据命题,画出图形;
F
2
3
1
A
B
C
D
E
(2)根据命题的条件、结论,结合图形,
写出已知、求证;
已知:AB∥CD;
求证:∠1 + ∠2 = 180°;
(3)写出证明过程.
证明:∵ AB∥CD(已知),
∴ ∠2=∠3(两直线平行,同位角相等),
∵ ∠1+∠3=180°(平角的定义),
∴ ∠1+∠2=180°(等量代换).
例8. 已知:AB∥CD,求证:∠A+∠C+∠AEC=360°.
F
)
1
)
2
证明:过E点作EF∥AB,
则∠A+∠1=180°(两直线平行平行,同旁内角互补)
∵AB∥CD(已知)
∴EF∥CD(平行于同一直线的两直线互相平行)
∴∠2+∠C=180°(两直线平行平行,同旁内角互补)
∴∠A+∠1+∠2+∠C=360°(等式的基本性质)
即∠A+∠C+∠AEC=360°
A
B
C
D
E
)
1
2
)
A
B
C
D
E
“铅笔头”模型
A
B
C
D
E
F
(三)与平行线的判定与性质相关的证明
变式1: 如图,AB∥CD,试用不同的方法证明∠AEC=∠A+∠C.
E
D
C
B
A
1
2
(
(
E
D
C
B
A
F
1
2
(
(
“猪蹄”模型
E
D
C
B
A
F
(三)与平行线的判定与性质相关的证明
(三)与平行线的判定与性质相关的证明
E
D
C
B
A
变式2: 如图,AB∥CD, ∠AEC与∠A、∠C 之间有怎样的数量关系?证明你的结论.
F
∠AEC=∠A-∠C
(三)与平行线的判定与性质相关的证明
变式3: 如图甲:已知AB∥DE,那么∠1+∠2+∠3等于多少度 试加以说明.
当已知条件不变,而图形变为如图乙时,结论改变了吗
图丙中的∠1+∠2+∠3+∠4是多少度呢?如果如丁图所示,∠1+∠2+∠3+…+∠n的和又为多少度?你找到了什么规律吗?
甲
乙
丙
丁
∠1+∠2+∠3=2×180°
∠1+∠2+∠3+∠4=3×180°
∠1+∠2+∠3+∠4+……+∠n=(n-1)×180°
E
D
C
B
A
B
A
D
C
E
F
(四)与三角形内角和定理相关的证明
例9: 将例8变式1的图中直线AB绕点A顺时针方向旋转一定角度交直线CD于点Q ,如下图,则∠AEC 、 ∠A、 ∠C、∠AFC 之间有何数量关系?
∠AEC= ∠A+∠C+∠AFC
“箭头”模型
P
变式1:在五角星ABCDE中,∠A、∠B、∠C、∠D、∠E的和等于多少度?请加以证明.
A
C
D
E
B
2
1
╮
╰
解:易证 ∠1+∠2=∠B+∠E
∵在△ACD中,
∠ A+∠ACD+∠ADC =180°
∴∠A+∠ACE+∠1+∠2+∠ADB=180°
即:∠A+ ∠B+ ∠C+ ∠D+ ∠E=180°
你还能想到其他证明方法吗?试一试 .
(四)与三角形内角和定理相关的证明
“8字”模型
变式2:把图1、图2叫蜕化的五角星,问它们的五角之和与五角星图形的五角之和仍相等吗?为什么?
(四)与三角形内角和定理相关的证明
D
A
E
C
(图1)
B
D
A
E
B
C
(图2)
相等
(四)与三角形内角和定理相关的证明
变式3:如图:求∠A+ ∠B+ ∠C+ ∠D+ ∠E+∠F的度数.
A
B
C
D
E
F
∠A+ ∠B+ ∠C+ ∠D+ ∠E+∠F=360°
巩固练习
1.下列关于判断一个数学结论是否正确的叙述中,正确的是( )
D
A. 只需观察得出
B. 只需依靠经验获得
C. 通过实验得出
D. 必须进行有根据的推理
2.下列平行线的判定方法中,是基本事实的是( )
A.同旁内角互补,两直线平行
B.同位角相等,两直线平行
C.内错角相等,两直线平行
D.在同一平面内,不相交的两条直线叫做平行线
B
3.如图,OP∥QR∥ST,则下列各式中正确的是( ).
A.∠1+∠2+∠3=180°
B.∠1+∠2-∠3=90°
C.∠1-∠2+∠3=90°
D.∠2+∠3-∠1=180°
D
Q
T
S
P
R
O
)
2
1
4
3
)
)
)
巩固练习
巩固练习
4. 如图,AB∥CD,EF⊥CD于点F.若∠BEF=150°,则∠ABE的度数为 60° .
60°
A
B
D
C
E
F
∟
巩固练习
5. 将一副三角尺按如图所示的方式摆放,且AB∥CD,则∠1的度数为 105 .
105°
A
B
C
1
∟
∟
D
巩固练习
6. 如图所示为可调躺椅示意图,AE与BD的交点为C,且∠A、∠B、∠E保持不变.为了舒适,需调整∠D的大小,使∠EFD=110°,则图中∠D应 减少 (填“增加”或“减少”) 10° .
减少
10°
C
B
A
D
E
F
50°
60°
20°
30°
巩固练习
7. 如图,AB∥DE,且∠1=∠2,∠3=∠4.求证:BC∥EF.
(1) 证明:∵ AB∥DE(已知),
∴ ∠1=∠3( 两直线平行,同位角相等 ).
∵ ∠1=∠2,∠3=∠4(已知),
∴ ∠2= ∠4 (等量代换).
∴ BC∥EF( 同位角相等,两直线平行 ).
(2) 上述推理过程中,运用的互逆的真命题是 “两直线平行,同位角相等”和“同位角相等,两直线平______ .
两直线平行,同位角相等
∠4
同位角相等,两直线平行
“两直线平行,同位角相等”
和“同位角相等,两直线平行”
A
B
C
D
E
2
F
1
3
4
8. 已知:如图,EF∥AD,∠1=∠2,∠BAC=70°.求∠AGD.
A
B
C
D
E
G
1
F
2
解:∵EF∥AD(已知),
∴∠2=∠3(两直线平行,同位角相等).
∵∠1=∠2(已知),
∴∠1=∠3(等量代换),
∴DG∥AB(内错角相等,两直线平行).
∴ ∠BAC+ ∠AGD=180°
(两直线平行,同旁内角互补)
∵∠BAC=70° (已知) ,
∴ ∠AGD=110° (等式性质) .
巩固练习
3
巩固练习
9.如图,在△ABC中,∠ACB=90°,AE是角平分线,CD是高,AE、CD相交于点F.
求证: ∠CFE= ∠CEF
C
∟
∟
A
B
D
E
F
证明:在△ACE、 △ADF中,
∵∠ACB=∠ADF=90°(已知),
∴∠CAE+ ∠CEF=90° 、∠DAF+ ∠AFD=90°
(直角三角形的两个锐角互余).
∵AE是角平分线(已知) ,
∴ ∠ CAE =∠ DAF (角平分线定义)
∴ ∠CEF = ∠ AFD(等式性质) .
∵ ∠CFE = ∠ AFD(对顶角相等) ,
∴ ∠CFE= ∠CEF (等量代换) .
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
