10.2直方图 课件(30张PPT)
图片预览










文档简介
(共30张PPT)
第10.2 直方图
人教版数学七年级下册
学习目标
1.认识直方图,会画直方图.会从直方图中读取数据蕴含的信息.
2.进一步熟悉数据的整理和表示的过程,掌握绘制频率分布直方图的方法.
3.培养在实际生活中的统计意识,感受统计知识的应用价值.
我们已经学习了用哪些方法来描述数据?
条形图 折线图 扇形图
各方法有什么特点?
复习引入
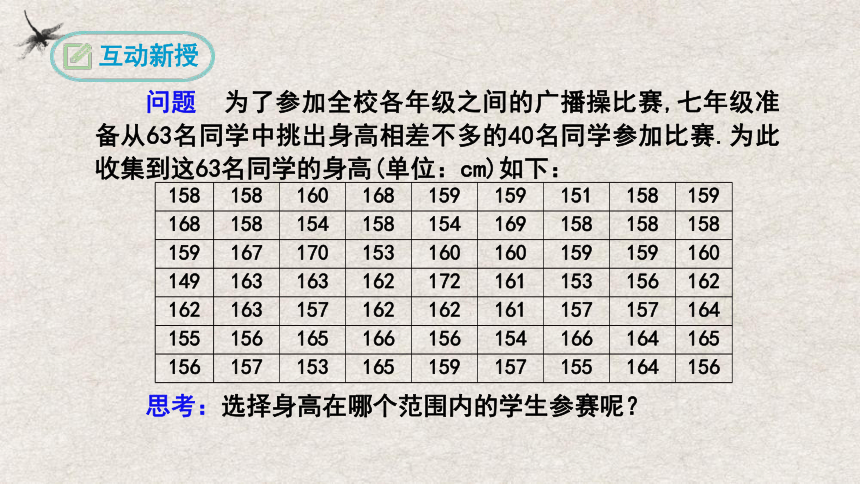
问题 为了参加全校各年级之间的广播操比赛,七年级准备从63名同学中挑出身高相差不多的40名同学参加比赛.为此收集到这63名同学的身高(单位:cm)如下:
158 158 160 168 159 159 151 158 159
168 158 154 158 154 169 158 158 158
159 167 170 153 160 160 159 159 160
149 163 163 162 172 161 153 156 162
162 163 157 162 162 161 157 157 164
155 156 165 166 156 154 166 164 165
156 157 153 165 159 157 155 164 156
思考:选择身高在哪个范围内的学生参赛呢?
互动新授
互动新授
为了使选取的参赛选手身高比较整齐,需要知道数据(身高)的分布情况,即在哪些身高范围的学生比较多,哪些身高范围内的学生比较少.
为此可以通过对这些数据适当分组来进行整理.
那如何进行分组呢?
在上面的数据中,最小值是149,最大值是172,它们的差是23,说明身高的变化范围是23 cm.
一、计算最大值和最小值的差
互动新授
二、决定组距和组数
所以要将数据分成8组:149≤x<152,152≤x<155,…,170≤x<173.这里组数和组距分别是8和3.
把所有数据分成若干组,每个小组的两个端点之间的距离称为组距.
根据问题的需要,各组的组距可以相同或不同.没有固定的标准,根据具体问题来决定.
本问题中我们作等距分组,即令各组的组距相同.如果从最小值起每隔3cm作为一个组,那么由于
互动新授
注意:组距和组数的确定没有固定的标准,要凭经验和研究的具体问题来决定.通常数据越多,分成的组数也越多,当数据在100个以内时,根据数据的多少通常分5~12个组.
对落在各个小组内的数据进行累计,得到各个小组内的数据的个数(叫做频数).整理可以得到频数分布表:
三、列频数分布表
互动新授
身高分组 划记 频数
149≤x<152 丅 2
152≤x<155 正 6
155≤x<158 正正丅 12
158≤x<161 正正正 19
161≤x<164 正正 10
164≤x<167 正 8
167≤x<170 4
170≤x<173 丅 2
从表中可以看出,身高在155≤x<158,158≤x<161,161≤x<164三个组的人数最多,一共有12+19+10=41人.
因此可以从身高在155cm至164 cm(不含164 cm)的同学中挑选参加比赛的同学.
互动新授
探究
上面对数据进行分组时,组距取3,把数据分成8组,如果组距取2或4,那么数据分成几个组?这样能否选出需要的40名同学呢?
互动新授
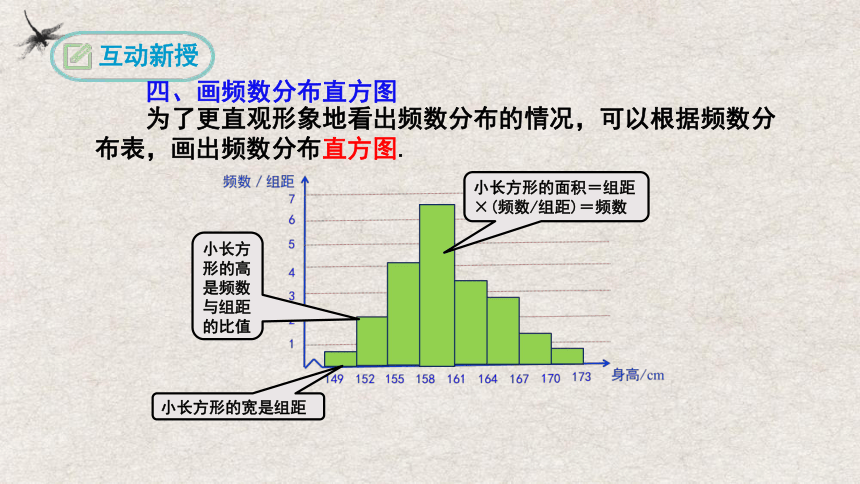
四、画频数分布直方图
为了更直观形象地看出频数分布的情况,可以根据频数分布表,画出频数分布直方图.
小长方形的高是频数与组距的比值
小长方形的宽是组距
小长方形的面积=组距×(频数/组距)=频数
互动新授
等距分组时,各小长方形的面积(频数)与高的比是常数(组距).因此,画等距分组的频数分布直方图时,为画图与看图的方便,通常直接用小长方形的高作为频数.
总结归纳
制作频数直方图大致步骤是什么?
(1)找出所给数据中的最大值和最小值,求最大值与最小值的差确定统计量的范围.
(2)确定组数和组距并进行分组.(数据个数在100以内,一般分5至12组)
(3)统计每组中数据的频数.
(4)根据分组和频数,绘制频数直方图.
例为了考察某种大麦穗长的分布情况,在一块试验田里抽取了100个麦穗,量得它们的长度如下表(单位:cm):
6.5 6.4 6.7 5.8 5.9 5.9 5.2 4.0 5.4 4.6
5.8 5.5 6.0 6.5 5.1 6.5 5.3 5.9 5.5 5.8
6.2 5.4 5.0 5.0 6.8 6.0 5.0 5.7 6.0 5.5
6.8 6.0 6.3 5.5 5.0 6.3 5.2 6.0 7.0 6.4
6.4 5.8 5.9 5.7 6.8 6.6 6.0 6.4 5.7 7.4
6.0 5.4 6.5 6.0 6.8 5.8 6.3 6.0 6.3 5.6
5.3 6.4 5.7 6.7 6.2 5.6 6.0 6.7 6.7 6.0
5.5 6.2 6.1 5.3 6.2 6.8 6.6 4.7 5.7 5.7
5.8 5.3 7.0 6.0 6.0 5.9 5.4 6.0 5.2 6.0
6.3 5.7 6.8 6.1 4.5 5.6 6.3 6.0 5.8 6.3
列出样本的频数分布表,画出频数分布直方图,从图表中可以得到什么信息?
典例精析
典例精析
解:(1)计算最大值和最小值的差.
在样本数据中,最大值是7.4,最小值是4.0,它们的差是
7.4-4.0=3.4.
(2)决定组距和组数.
最大值与最小值的差是3.4 ,如果取组距为0.3 cm,那么由于
可以分成12组,组数合适,于是取组距为0.3 ,组数为12.
典例精析
(3)列频数分布表
分组 划记 频数
4.0≤x<4.3 一 1
4.3≤x<4.6 一 1
4.6≤x<4.9 丅 2
4.9≤x<5.2 正 5
5.2≤x<5.5 正正 11
5.5≤x<5.8 正正正 15
5.8≤x<6.1 正正正正正 28
6.1≤x<6.4 正正 13
6.4≤x<6.7 正正 11
6.7≤x<7.0 正正 10
7.0≤x<7.3 丅 2
7.3≤x<7.6 一 1
合计 100
典例精析
(4)画频数分布直方图
从表和图中可以看出,麦穗长度大部分落在5.2 cm至7.0 cm之间,其他范围较少.长度在5.8≤x<6.1范围内的麦穗根数最多,有28根,而长度在4.0≤x<4.3,4.3≤x<4.6,4.6≤x<4.9,7.0≤x<7.3,7.3≤x<7.6范围内的麦穗根数很少,总共只有7根.
1.陈老师对56名同学的跳绳成绩进行了统计,跳绳个数140个以上的有28名同学,则跳绳个数140个以上的频率为( )
A.0.4 B.0.2 C.0.5 D.2
C
小试牛刀
2.一个样本有100个数据,最大值为7.4,最小值为4.0,如果取组距为0.3,那么这组数据可分成( )
A.11组 B.12组
C.13组 D.以上答案均不对
B
小试牛刀
1.在频数分布表中,各小组的频数之和( )
A.小于数据总数 B.等于数据总数
C.大于数据总数 D.不能确定
2.如图是某班45名同学爱心捐款额的频数直方图(每组含前一个边界值,不含后一个边界值),则捐款人数最多的一组是( )
A.5~10元 B.10~15元
C.15~20元 D.20~25元
B
C
课堂检测
3.某校为加强学生安全意识,组织全校学生参加安全知识竞赛。从中抽取部分学生成绩(得分取正整数值,满分为100分)进行统计,绘制以下两幅不完整的统计图.
请根据图中的信息,解决下列问题:
(1)填空:a=_____,n=_____;
(2)补全频数直方图;
(3)该校共有2000名学生.若成绩在80分以下(含80分)的学生安全意识不强,则该校安全意识不强的学生约有多少人?
课堂检测
解:(1)∵本次调查的总人数为30÷10%=300(人),
∴a=300×25%=75,D组所占百分比为,
所以E组的百分比为1-10%-20%-25%-30%=15%,则n=360°×15%=54°,
(2)B组人数为300×20%=60(人),补全频数分布直方图如下:
(3)2000×(10%+20%+25%)=1100,
答:该校安全意识不强的学生约有1100人.
课堂检测
1.暑期将至,某校组织学生进行“防溺水”安全知识竞赛,老师从中随机抽取了部分学生的成绩(得分取整数,满分为100分),整理后绘制成如图所示的不完整的扇形统计图和频数分布直方图.
拓展训练
其中A组的频数a比B组的频数b小15.请根据以上信息,解答下列问题:
(1)本次共抽取 名学生,a的值为 ;
(2)在扇形统计图中,n= ,E组所占比例为 %;
(3)补全频数分布直方图;
(4)若全校共有1500名学生,请根据抽样调查的结果,估计成绩在80分以上的学生人数.
拓展训练
解:(1)A组的频数a比B组的频数b小15,A组的频率比B组的频率小18%-8%=10%,
因此调查人数为:15÷(18%-8%)=150(人),
a=150×8%=12(人),
故答案为:150,12;
(2) ,即n=144,
“E组”所占的百分比为1-8%-18%-30%-40%=4%,
故答案为:144,4;
拓展训练
(3)b= a+15=27(人),
“C组”频数为:150×30%=45(人),
“E组”频数为:150×4%=6(人),
补全频数分布直方图如图所示:
(4) (人),
答:估计成绩在80分以上的学生人数大约为660人.
拓展训练
条形统计图与频数分布直方图的关系:
不同点:
(1)频数分布直方图是一种以频数为纵向指标的条形统计图;
(2)频数分布直方图中的长方形是连续排列的,条形统计图中的长方形是分开排列的.
相同点:都易于比较各组数据之间的差别,能直观
地显示各组数据之间具体数据的分布情况.
课堂小结
1.在对七年级某班的一次数学测验成绩进行统计分析中,各分数段的人数如图所示(分数取正整数,满分100分),请观察图形,并回答下列问题.
(1)该班有 名学生;
(2)70.5~80.5这一组的频数是 ,频率是 ;
(3)请你估算该班这次测验的平均成绩是 .
44
14
0.32
80
人数
分数
50.5
60.5
70.5
80.5
90.5
100.5
课后作业
2.某中学九年级部分同学参加全国初中数学竞赛,指导老师统计了所有参赛同学的成绩(成绩都是整数,试题满分120分),并且绘制了频数分布直方图,如图所示,请根据直方图回答下列问题:
(1)该中学参加本次数
学竞赛的有多少名同学?
(2)如果成绩在90分以上(含
90分)的同学获奖,那么该中学
参赛同学的获奖率是多少?
(3)图中还提供了其他数据,例如该中学没有获得满分的同学等等.请再写出两条信息.
60
70
80
90
100
110
120
人数
分数)
课后作业
(1)该中学参加本次数学竞赛的有多少名同学?
(2)如果成绩在90分以上(含90分)的同学获奖,那么该中学参赛同学的获奖率是多少?
(3)图中还提供了其他数据,例如该中学没有获得满分的同学等等.请再写出两条信息.
解:(1)4+6+8+7+5+2=32,所以参加本次数学竞赛的有32名同学;
(2)(7+5+2)÷32=43.75%,所以该中学的参赛同学获奖率是43.75%;
(3)该中学参赛同学的成绩均不低于60分;成绩在80~90分数段的人数最多.
课后作业
谢谢聆听
第10.2 直方图
人教版数学七年级下册
学习目标
1.认识直方图,会画直方图.会从直方图中读取数据蕴含的信息.
2.进一步熟悉数据的整理和表示的过程,掌握绘制频率分布直方图的方法.
3.培养在实际生活中的统计意识,感受统计知识的应用价值.
我们已经学习了用哪些方法来描述数据?
条形图 折线图 扇形图
各方法有什么特点?
复习引入
问题 为了参加全校各年级之间的广播操比赛,七年级准备从63名同学中挑出身高相差不多的40名同学参加比赛.为此收集到这63名同学的身高(单位:cm)如下:
158 158 160 168 159 159 151 158 159
168 158 154 158 154 169 158 158 158
159 167 170 153 160 160 159 159 160
149 163 163 162 172 161 153 156 162
162 163 157 162 162 161 157 157 164
155 156 165 166 156 154 166 164 165
156 157 153 165 159 157 155 164 156
思考:选择身高在哪个范围内的学生参赛呢?
互动新授
互动新授
为了使选取的参赛选手身高比较整齐,需要知道数据(身高)的分布情况,即在哪些身高范围的学生比较多,哪些身高范围内的学生比较少.
为此可以通过对这些数据适当分组来进行整理.
那如何进行分组呢?
在上面的数据中,最小值是149,最大值是172,它们的差是23,说明身高的变化范围是23 cm.
一、计算最大值和最小值的差
互动新授
二、决定组距和组数
所以要将数据分成8组:149≤x<152,152≤x<155,…,170≤x<173.这里组数和组距分别是8和3.
把所有数据分成若干组,每个小组的两个端点之间的距离称为组距.
根据问题的需要,各组的组距可以相同或不同.没有固定的标准,根据具体问题来决定.
本问题中我们作等距分组,即令各组的组距相同.如果从最小值起每隔3cm作为一个组,那么由于
互动新授
注意:组距和组数的确定没有固定的标准,要凭经验和研究的具体问题来决定.通常数据越多,分成的组数也越多,当数据在100个以内时,根据数据的多少通常分5~12个组.
对落在各个小组内的数据进行累计,得到各个小组内的数据的个数(叫做频数).整理可以得到频数分布表:
三、列频数分布表
互动新授
身高分组 划记 频数
149≤x<152 丅 2
152≤x<155 正 6
155≤x<158 正正丅 12
158≤x<161 正正正 19
161≤x<164 正正 10
164≤x<167 正 8
167≤x<170 4
170≤x<173 丅 2
从表中可以看出,身高在155≤x<158,158≤x<161,161≤x<164三个组的人数最多,一共有12+19+10=41人.
因此可以从身高在155cm至164 cm(不含164 cm)的同学中挑选参加比赛的同学.
互动新授
探究
上面对数据进行分组时,组距取3,把数据分成8组,如果组距取2或4,那么数据分成几个组?这样能否选出需要的40名同学呢?
互动新授
四、画频数分布直方图
为了更直观形象地看出频数分布的情况,可以根据频数分布表,画出频数分布直方图.
小长方形的高是频数与组距的比值
小长方形的宽是组距
小长方形的面积=组距×(频数/组距)=频数
互动新授
等距分组时,各小长方形的面积(频数)与高的比是常数(组距).因此,画等距分组的频数分布直方图时,为画图与看图的方便,通常直接用小长方形的高作为频数.
总结归纳
制作频数直方图大致步骤是什么?
(1)找出所给数据中的最大值和最小值,求最大值与最小值的差确定统计量的范围.
(2)确定组数和组距并进行分组.(数据个数在100以内,一般分5至12组)
(3)统计每组中数据的频数.
(4)根据分组和频数,绘制频数直方图.
例为了考察某种大麦穗长的分布情况,在一块试验田里抽取了100个麦穗,量得它们的长度如下表(单位:cm):
6.5 6.4 6.7 5.8 5.9 5.9 5.2 4.0 5.4 4.6
5.8 5.5 6.0 6.5 5.1 6.5 5.3 5.9 5.5 5.8
6.2 5.4 5.0 5.0 6.8 6.0 5.0 5.7 6.0 5.5
6.8 6.0 6.3 5.5 5.0 6.3 5.2 6.0 7.0 6.4
6.4 5.8 5.9 5.7 6.8 6.6 6.0 6.4 5.7 7.4
6.0 5.4 6.5 6.0 6.8 5.8 6.3 6.0 6.3 5.6
5.3 6.4 5.7 6.7 6.2 5.6 6.0 6.7 6.7 6.0
5.5 6.2 6.1 5.3 6.2 6.8 6.6 4.7 5.7 5.7
5.8 5.3 7.0 6.0 6.0 5.9 5.4 6.0 5.2 6.0
6.3 5.7 6.8 6.1 4.5 5.6 6.3 6.0 5.8 6.3
列出样本的频数分布表,画出频数分布直方图,从图表中可以得到什么信息?
典例精析
典例精析
解:(1)计算最大值和最小值的差.
在样本数据中,最大值是7.4,最小值是4.0,它们的差是
7.4-4.0=3.4.
(2)决定组距和组数.
最大值与最小值的差是3.4 ,如果取组距为0.3 cm,那么由于
可以分成12组,组数合适,于是取组距为0.3 ,组数为12.
典例精析
(3)列频数分布表
分组 划记 频数
4.0≤x<4.3 一 1
4.3≤x<4.6 一 1
4.6≤x<4.9 丅 2
4.9≤x<5.2 正 5
5.2≤x<5.5 正正 11
5.5≤x<5.8 正正正 15
5.8≤x<6.1 正正正正正 28
6.1≤x<6.4 正正 13
6.4≤x<6.7 正正 11
6.7≤x<7.0 正正 10
7.0≤x<7.3 丅 2
7.3≤x<7.6 一 1
合计 100
典例精析
(4)画频数分布直方图
从表和图中可以看出,麦穗长度大部分落在5.2 cm至7.0 cm之间,其他范围较少.长度在5.8≤x<6.1范围内的麦穗根数最多,有28根,而长度在4.0≤x<4.3,4.3≤x<4.6,4.6≤x<4.9,7.0≤x<7.3,7.3≤x<7.6范围内的麦穗根数很少,总共只有7根.
1.陈老师对56名同学的跳绳成绩进行了统计,跳绳个数140个以上的有28名同学,则跳绳个数140个以上的频率为( )
A.0.4 B.0.2 C.0.5 D.2
C
小试牛刀
2.一个样本有100个数据,最大值为7.4,最小值为4.0,如果取组距为0.3,那么这组数据可分成( )
A.11组 B.12组
C.13组 D.以上答案均不对
B
小试牛刀
1.在频数分布表中,各小组的频数之和( )
A.小于数据总数 B.等于数据总数
C.大于数据总数 D.不能确定
2.如图是某班45名同学爱心捐款额的频数直方图(每组含前一个边界值,不含后一个边界值),则捐款人数最多的一组是( )
A.5~10元 B.10~15元
C.15~20元 D.20~25元
B
C
课堂检测
3.某校为加强学生安全意识,组织全校学生参加安全知识竞赛。从中抽取部分学生成绩(得分取正整数值,满分为100分)进行统计,绘制以下两幅不完整的统计图.
请根据图中的信息,解决下列问题:
(1)填空:a=_____,n=_____;
(2)补全频数直方图;
(3)该校共有2000名学生.若成绩在80分以下(含80分)的学生安全意识不强,则该校安全意识不强的学生约有多少人?
课堂检测
解:(1)∵本次调查的总人数为30÷10%=300(人),
∴a=300×25%=75,D组所占百分比为,
所以E组的百分比为1-10%-20%-25%-30%=15%,则n=360°×15%=54°,
(2)B组人数为300×20%=60(人),补全频数分布直方图如下:
(3)2000×(10%+20%+25%)=1100,
答:该校安全意识不强的学生约有1100人.
课堂检测
1.暑期将至,某校组织学生进行“防溺水”安全知识竞赛,老师从中随机抽取了部分学生的成绩(得分取整数,满分为100分),整理后绘制成如图所示的不完整的扇形统计图和频数分布直方图.
拓展训练
其中A组的频数a比B组的频数b小15.请根据以上信息,解答下列问题:
(1)本次共抽取 名学生,a的值为 ;
(2)在扇形统计图中,n= ,E组所占比例为 %;
(3)补全频数分布直方图;
(4)若全校共有1500名学生,请根据抽样调查的结果,估计成绩在80分以上的学生人数.
拓展训练
解:(1)A组的频数a比B组的频数b小15,A组的频率比B组的频率小18%-8%=10%,
因此调查人数为:15÷(18%-8%)=150(人),
a=150×8%=12(人),
故答案为:150,12;
(2) ,即n=144,
“E组”所占的百分比为1-8%-18%-30%-40%=4%,
故答案为:144,4;
拓展训练
(3)b= a+15=27(人),
“C组”频数为:150×30%=45(人),
“E组”频数为:150×4%=6(人),
补全频数分布直方图如图所示:
(4) (人),
答:估计成绩在80分以上的学生人数大约为660人.
拓展训练
条形统计图与频数分布直方图的关系:
不同点:
(1)频数分布直方图是一种以频数为纵向指标的条形统计图;
(2)频数分布直方图中的长方形是连续排列的,条形统计图中的长方形是分开排列的.
相同点:都易于比较各组数据之间的差别,能直观
地显示各组数据之间具体数据的分布情况.
课堂小结
1.在对七年级某班的一次数学测验成绩进行统计分析中,各分数段的人数如图所示(分数取正整数,满分100分),请观察图形,并回答下列问题.
(1)该班有 名学生;
(2)70.5~80.5这一组的频数是 ,频率是 ;
(3)请你估算该班这次测验的平均成绩是 .
44
14
0.32
80
人数
分数
50.5
60.5
70.5
80.5
90.5
100.5
课后作业
2.某中学九年级部分同学参加全国初中数学竞赛,指导老师统计了所有参赛同学的成绩(成绩都是整数,试题满分120分),并且绘制了频数分布直方图,如图所示,请根据直方图回答下列问题:
(1)该中学参加本次数
学竞赛的有多少名同学?
(2)如果成绩在90分以上(含
90分)的同学获奖,那么该中学
参赛同学的获奖率是多少?
(3)图中还提供了其他数据,例如该中学没有获得满分的同学等等.请再写出两条信息.
60
70
80
90
100
110
120
人数
分数)
课后作业
(1)该中学参加本次数学竞赛的有多少名同学?
(2)如果成绩在90分以上(含90分)的同学获奖,那么该中学参赛同学的获奖率是多少?
(3)图中还提供了其他数据,例如该中学没有获得满分的同学等等.请再写出两条信息.
解:(1)4+6+8+7+5+2=32,所以参加本次数学竞赛的有32名同学;
(2)(7+5+2)÷32=43.75%,所以该中学的参赛同学获奖率是43.75%;
(3)该中学参赛同学的成绩均不低于60分;成绩在80~90分数段的人数最多.
课后作业
谢谢聆听
