15.1平面直角坐标系(第1课时)课件(24张PPT)
文档属性
| 名称 | 15.1平面直角坐标系(第1课时)课件(24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 763.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-10 00:00:00 | ||
图片预览








文档简介
(共24张PPT)
2022-2023学年七年级数学下册同步精品课堂(沪教版)
15.1平面直角坐标系(第1课时)
第 15章平面直角坐标系
我们在第十二章关于实数的学习中知道,每一个实数都可以用数轴上唯一的一个点来表示;反过来,数轴上的每一个点也都可以用唯一的一个实数来表示,在数学上就说数轴上的所有点与实数的全体有一一对应的关系。这样把“数”与“形”相互联系起来,对我们研究数学问题有很大的帮助。
那么,平面上的点能不能用实数来表示 观察下面的图片,整齐的队伍中每一个战士所在的位置可以用行数和列数来表示,电影院里的座位也可以用排数和号数来表示,它会使我们对于用实数来表示平面上一个点的位置产生联想.
怎样建立平面上的点与实数的联系 怎样用数学的语言和方法来表达 这就是我们在本章学习的内容.
我们知道,在直线上规定了原点、正方向和单位长度,这直线就是一条数轴;数轴上的所有点与全体实数之间具有对应的关系。这一对应关系得以建立,它的基础是在直线上选取了一个点为基点(原点),同时规定正方向,使直线上的点位于基点两侧的分布状况可与实数有正、负之分的符号特征相联系;基点为分界点。而规定了单位长度,使直线上的点与基点的距离可与实数的绝对值相联系
方格中有25个字,若用A4表示“书”,
有
B4
1、请破译下列密码:
A5 B5 C4 E5 B1 C2
天 才 来 自 勤 奋
2、请编制密码:
志
者
事
竟
成
D2
E3
C5
D4
C3
5
有
志
自
万
事
4
天
3
标
宝
奋
可
2
敏
大
1
的
B
E
想
D
库
才
成
A
书
里
来
贵
打
者
勤
竟
C
课前导入
能向家长介绍你的座位在教室中的位置吗?
如果将“2组3排”简记作(2,3),
那么“3组4排”如何表示?
(5,3)表示什么含义?
(3,4)
5组3排
那么“3排4组”如何表示?
(4,3)
or
(4,3)
(3,4)
问题
怎样建立平面上的点与实数之间的联系呢
平面是向各方无限伸展的。 平面内有无数多条直线,每条直线上又有无数多个点,因此平面内的所有点不能像直线上的点那样用一个实数来表示
电影院里的座位标明了排数和号数,观众根据电影票可以在电影院里找到被指定的座位。这就是说,电影院里的每个座位与由有序的两个正整数组成的一个“数对”建立了对应关系。由此联想,可以考虑用“数对”来表示平面内的点.把有序的两个正整数所组成的“数对”扩大为由有序的两个非零实数组成的“数对”,那么它们的正、负号组合情况有四种,而两条相交直线把平面分为四个区域,可使平面内的点的分布状况与“数对”的符号组合情况相联系;两条直线为分界线.
在平面内取一点0,过点 0 画两条互相垂直的数轴,目使它们以点0为公共原点。这样,就在平面内建立了一个直角坐标系(orthogonal coordinate system).通常,所画的两条数轴中,有一条是水平放置的,它的正方向向右,这条数轴叫做横轴(abscissa axis)(记作x轴);另一条是铅直放置的,它的正方向向上,这条数轴叫做纵轴(ordinate axis)(记作y轴)如图15-1所示,记作平面直角坐标系xOy;点O叫做坐标原点(简称原点),x轴和y轴统称为坐标轴
建立了直角坐标系的平面叫做直角坐标平面(简称坐标平面).这样,原来平面内的点都可以用有序实数对来表示
1.两条数轴
平面直角坐标系xOy:
2.互相垂直
3.公共原点
4.正方向
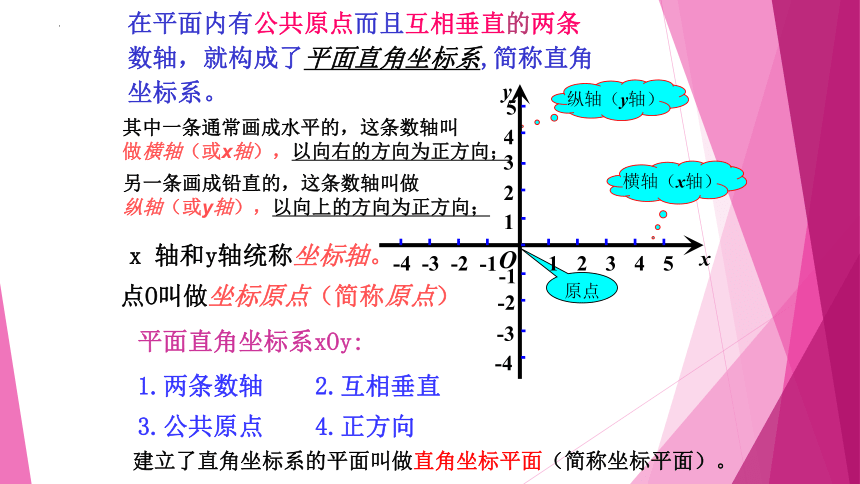
在平面内有公共原点而且互相垂直的两条数轴,就构成了平面直角坐标系,简称直角坐标系。
其中一条通常画成水平的,这条数轴叫
做横轴(或x轴),以向右的方向为正方向;
另一条画成铅直的,这条数轴叫做
纵轴(或y轴),以向上的方向为正方向;
纵轴(y轴)
横轴(x轴)
原点
O
x
1
2
3
4
5
-4
-3
-2
-1
y
3
1
4
2
5
-2
-4
-1
-3
点O叫做坐标原点(简称原点)
x 轴和y轴统称坐标轴。
建立了直角坐标系的平面叫做直角坐标平面(简称坐标平面)。
操作1
已知直角坐标平面内一点A,用下面的方法可确定表示点A的“数对”:
如图15-2过点A作x轴的垂线垂足为A1,得到A1在x轴上所对应的实数是3;再过点A作y轴的垂线,垂足为A2,得到A2在y轴上所对应的实数是2.5. 因为过一点作已知直线的垂线能且只能作一条,所以A1 、A2,是唯一确定的,可知A1、A2,分别所对应的实数3和2.5也是唯一确定的。把3写在前,2.5写在后,组成“有序实数对”,记为(3,2.5),那么(3,2.5)就表示点A.
一般地,对于直角坐标平面内的任意一点P,如图15-3过点P作x轴的垂线,垂足为M,可得点M在x轴上所对应的实数a;再过点P作v轴的垂线,垂足为N,可得点N在轴上所对应的实数6,那么有序实数对(a,b)表示点P,这样的有序实数对是唯一确定的。反过来,任意给定一对有序实数(a,b),可在x轴上描出实数a所对应的点M,在y轴上描出实数6所对应的点N;再过点M作x轴的垂线,过点N作Y轴的垂线,那么这两条垂线的交点P表示有序实数对(a,b),这样的点也是唯一确定的于是,平面内的每一点都有唯一的有序实数对与它对应
在(a,b)中,a、b 的顺序不能颠倒.当a头6 时,(a,b)与(b,a)表示不同的点.
在平面直角坐标系 xOy 中,点 P所对应的有序实数对(a,b)叫做点 P的坐标,记作 P(a,b),其中a 叫做横坐标(abscissa),b 叫做纵坐标(ordinate).
原点 0的坐标是(0,0)
平面上点的表示:
.
P
平面内任意一点P,过P点分别
向x、y轴作垂线,垂足在x轴、
y轴上对应的数a、b分别叫做
点P的横坐标、纵坐标,
则有序实数对(a,b)叫做点P的坐标。
a
b
记作:P(a,b)
O
x
y
注意:横坐标写在前,纵坐标写在后,
中间用逗号隔开.
(a,b)
O
-3 -2
-1
-4
1
2
-1
-2
x
y
2 3
4
1
3
-3
A
( , )
2
3
B
( , )
3
2
A1
A2
B1
B2
注意:
(a,b)是一对有序实数对,横坐标在前,纵坐标在后,中间用逗号隔开,不能颠倒。
归纳:平面内一个点的位置可以用
一对有序实数对来表示。
例题1 写出图15-4中直角坐标平面内各点的坐标
解 过点A 作x轴的线,垂足在x 轴上对应的实数是 3;再过点A 作y轴的垂线,垂足在r轴上对应的实数是4,所以点 A 的坐标是(3,4).
同理,点 B 的坐标是(-3,1);
点 C 的坐标是(-2,-3);
点 D的坐标是(5,-2).
例题2 写出图15-5中坐标轴上的点 E、F的坐标
解 过点E作x轴的垂线,垂足为 E,点E在x轴上对应的实数是-4;过点E作y轴的垂线,垂足为 0,点0在轴上对应的实数是 0.因此点E的横坐标是 -4,纵坐标是 0,所以点 E的坐标是(-4,0).
用同样的方法可以得到点F的坐标是(0,2)
课本练习
1.写出图中A、B、C、D、E、F各点的坐标
2.写出图中点A、B、C、D、E、F、G的坐标
3.在直角坐标平面内,横坐标与纵坐标都是整数的点叫做格点;顶点都是格点的三角形叫做格点三角形.已知格点A (-2,1),B(1,3),C(2,1),请在图中画出以A、B、C为顶点的格点三角形,并求△ABC的面积
随堂检测
1.下列四个图形中,建立直角坐标平面正确的是( )
x
(D)
y
1
2
3
-1
-2
-3
1
2
3
-1
-2
-3
O
x
(C)
y
1
2
3
-1
-2
-3
1
2
3
-1
-2
-3
O
x
(B)
y
2
3
4
O
-1
-2
2
3
4
O
-1
-2
1
y
x
1
2
3
-1
-2
-3
(A)
1
2
3
-1
-2
-3
O
D
·
A
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
横轴
y
纵轴
(3,2)
·
C
C(1,- 4)
方法:先横后纵
B
B(2,3)
是有序实数对
D
E
(-3,-3)
(5,-3)
3叫做点A的横坐标
2叫做点A的纵坐标
A点在平面内的坐标为(3, 2)
记作:A(3,2)
先横后纵加括号,
中间逗号要隔开
2.写出直角坐标平面
内各点的坐标.
5
-5
-2
-3
-4
-1
3
2
4
1
-6
6
y
-5
5
-3
-4
4
-2
3
-1
2
1
-6
6
o
x
x轴上的点,纵坐标都是0;
·
·
·
·
A
B
C
A(-4,0)
B(4,0)
O(0,0)
C(6,0)
·
·
·
D
E
F
D(0,4)
y轴上的点,横坐标都是0。
O(0,0)
E(0,-3)
F(0,-5)
O
3.写出直角坐标平面
内各点的坐标.
0
1
2
3
4
5
-4
-3
-2
-1
·
C
3
1
4
2
5
-2
-4
-1
-3
x
横轴
y
纵轴
·
B
·
A
·
D
4.描出下列各点:
A(4,3),B(-2,3),C(-4,-1),D(2,-2)
方法:先横后纵
本节课我们学面直角坐标系。学习本节我们要掌握以下三方面的内容:
1、能够正确画出直角坐标系。
2、能在直角坐标系中,根据坐标找出点,
由点求出坐标。
3、x轴上的点的纵坐标为0,表示为(x,0)
y轴上的点的横坐标为0,表示为(0,y)
课堂小结
2022-2023学年七年级数学下册同步精品课堂(沪教版)
15.1平面直角坐标系(第1课时)
第 15章平面直角坐标系
我们在第十二章关于实数的学习中知道,每一个实数都可以用数轴上唯一的一个点来表示;反过来,数轴上的每一个点也都可以用唯一的一个实数来表示,在数学上就说数轴上的所有点与实数的全体有一一对应的关系。这样把“数”与“形”相互联系起来,对我们研究数学问题有很大的帮助。
那么,平面上的点能不能用实数来表示 观察下面的图片,整齐的队伍中每一个战士所在的位置可以用行数和列数来表示,电影院里的座位也可以用排数和号数来表示,它会使我们对于用实数来表示平面上一个点的位置产生联想.
怎样建立平面上的点与实数的联系 怎样用数学的语言和方法来表达 这就是我们在本章学习的内容.
我们知道,在直线上规定了原点、正方向和单位长度,这直线就是一条数轴;数轴上的所有点与全体实数之间具有对应的关系。这一对应关系得以建立,它的基础是在直线上选取了一个点为基点(原点),同时规定正方向,使直线上的点位于基点两侧的分布状况可与实数有正、负之分的符号特征相联系;基点为分界点。而规定了单位长度,使直线上的点与基点的距离可与实数的绝对值相联系
方格中有25个字,若用A4表示“书”,
有
B4
1、请破译下列密码:
A5 B5 C4 E5 B1 C2
天 才 来 自 勤 奋
2、请编制密码:
志
者
事
竟
成
D2
E3
C5
D4
C3
5
有
志
自
万
事
4
天
3
标
宝
奋
可
2
敏
大
1
的
B
E
想
D
库
才
成
A
书
里
来
贵
打
者
勤
竟
C
课前导入
能向家长介绍你的座位在教室中的位置吗?
如果将“2组3排”简记作(2,3),
那么“3组4排”如何表示?
(5,3)表示什么含义?
(3,4)
5组3排
那么“3排4组”如何表示?
(4,3)
or
(4,3)
(3,4)
问题
怎样建立平面上的点与实数之间的联系呢
平面是向各方无限伸展的。 平面内有无数多条直线,每条直线上又有无数多个点,因此平面内的所有点不能像直线上的点那样用一个实数来表示
电影院里的座位标明了排数和号数,观众根据电影票可以在电影院里找到被指定的座位。这就是说,电影院里的每个座位与由有序的两个正整数组成的一个“数对”建立了对应关系。由此联想,可以考虑用“数对”来表示平面内的点.把有序的两个正整数所组成的“数对”扩大为由有序的两个非零实数组成的“数对”,那么它们的正、负号组合情况有四种,而两条相交直线把平面分为四个区域,可使平面内的点的分布状况与“数对”的符号组合情况相联系;两条直线为分界线.
在平面内取一点0,过点 0 画两条互相垂直的数轴,目使它们以点0为公共原点。这样,就在平面内建立了一个直角坐标系(orthogonal coordinate system).通常,所画的两条数轴中,有一条是水平放置的,它的正方向向右,这条数轴叫做横轴(abscissa axis)(记作x轴);另一条是铅直放置的,它的正方向向上,这条数轴叫做纵轴(ordinate axis)(记作y轴)如图15-1所示,记作平面直角坐标系xOy;点O叫做坐标原点(简称原点),x轴和y轴统称为坐标轴
建立了直角坐标系的平面叫做直角坐标平面(简称坐标平面).这样,原来平面内的点都可以用有序实数对来表示
1.两条数轴
平面直角坐标系xOy:
2.互相垂直
3.公共原点
4.正方向
在平面内有公共原点而且互相垂直的两条数轴,就构成了平面直角坐标系,简称直角坐标系。
其中一条通常画成水平的,这条数轴叫
做横轴(或x轴),以向右的方向为正方向;
另一条画成铅直的,这条数轴叫做
纵轴(或y轴),以向上的方向为正方向;
纵轴(y轴)
横轴(x轴)
原点
O
x
1
2
3
4
5
-4
-3
-2
-1
y
3
1
4
2
5
-2
-4
-1
-3
点O叫做坐标原点(简称原点)
x 轴和y轴统称坐标轴。
建立了直角坐标系的平面叫做直角坐标平面(简称坐标平面)。
操作1
已知直角坐标平面内一点A,用下面的方法可确定表示点A的“数对”:
如图15-2过点A作x轴的垂线垂足为A1,得到A1在x轴上所对应的实数是3;再过点A作y轴的垂线,垂足为A2,得到A2在y轴上所对应的实数是2.5. 因为过一点作已知直线的垂线能且只能作一条,所以A1 、A2,是唯一确定的,可知A1、A2,分别所对应的实数3和2.5也是唯一确定的。把3写在前,2.5写在后,组成“有序实数对”,记为(3,2.5),那么(3,2.5)就表示点A.
一般地,对于直角坐标平面内的任意一点P,如图15-3过点P作x轴的垂线,垂足为M,可得点M在x轴上所对应的实数a;再过点P作v轴的垂线,垂足为N,可得点N在轴上所对应的实数6,那么有序实数对(a,b)表示点P,这样的有序实数对是唯一确定的。反过来,任意给定一对有序实数(a,b),可在x轴上描出实数a所对应的点M,在y轴上描出实数6所对应的点N;再过点M作x轴的垂线,过点N作Y轴的垂线,那么这两条垂线的交点P表示有序实数对(a,b),这样的点也是唯一确定的于是,平面内的每一点都有唯一的有序实数对与它对应
在(a,b)中,a、b 的顺序不能颠倒.当a头6 时,(a,b)与(b,a)表示不同的点.
在平面直角坐标系 xOy 中,点 P所对应的有序实数对(a,b)叫做点 P的坐标,记作 P(a,b),其中a 叫做横坐标(abscissa),b 叫做纵坐标(ordinate).
原点 0的坐标是(0,0)
平面上点的表示:
.
P
平面内任意一点P,过P点分别
向x、y轴作垂线,垂足在x轴、
y轴上对应的数a、b分别叫做
点P的横坐标、纵坐标,
则有序实数对(a,b)叫做点P的坐标。
a
b
记作:P(a,b)
O
x
y
注意:横坐标写在前,纵坐标写在后,
中间用逗号隔开.
(a,b)
O
-3 -2
-1
-4
1
2
-1
-2
x
y
2 3
4
1
3
-3
A
( , )
2
3
B
( , )
3
2
A1
A2
B1
B2
注意:
(a,b)是一对有序实数对,横坐标在前,纵坐标在后,中间用逗号隔开,不能颠倒。
归纳:平面内一个点的位置可以用
一对有序实数对来表示。
例题1 写出图15-4中直角坐标平面内各点的坐标
解 过点A 作x轴的线,垂足在x 轴上对应的实数是 3;再过点A 作y轴的垂线,垂足在r轴上对应的实数是4,所以点 A 的坐标是(3,4).
同理,点 B 的坐标是(-3,1);
点 C 的坐标是(-2,-3);
点 D的坐标是(5,-2).
例题2 写出图15-5中坐标轴上的点 E、F的坐标
解 过点E作x轴的垂线,垂足为 E,点E在x轴上对应的实数是-4;过点E作y轴的垂线,垂足为 0,点0在轴上对应的实数是 0.因此点E的横坐标是 -4,纵坐标是 0,所以点 E的坐标是(-4,0).
用同样的方法可以得到点F的坐标是(0,2)
课本练习
1.写出图中A、B、C、D、E、F各点的坐标
2.写出图中点A、B、C、D、E、F、G的坐标
3.在直角坐标平面内,横坐标与纵坐标都是整数的点叫做格点;顶点都是格点的三角形叫做格点三角形.已知格点A (-2,1),B(1,3),C(2,1),请在图中画出以A、B、C为顶点的格点三角形,并求△ABC的面积
随堂检测
1.下列四个图形中,建立直角坐标平面正确的是( )
x
(D)
y
1
2
3
-1
-2
-3
1
2
3
-1
-2
-3
O
x
(C)
y
1
2
3
-1
-2
-3
1
2
3
-1
-2
-3
O
x
(B)
y
2
3
4
O
-1
-2
2
3
4
O
-1
-2
1
y
x
1
2
3
-1
-2
-3
(A)
1
2
3
-1
-2
-3
O
D
·
A
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
横轴
y
纵轴
(3,2)
·
C
C(1,- 4)
方法:先横后纵
B
B(2,3)
是有序实数对
D
E
(-3,-3)
(5,-3)
3叫做点A的横坐标
2叫做点A的纵坐标
A点在平面内的坐标为(3, 2)
记作:A(3,2)
先横后纵加括号,
中间逗号要隔开
2.写出直角坐标平面
内各点的坐标.
5
-5
-2
-3
-4
-1
3
2
4
1
-6
6
y
-5
5
-3
-4
4
-2
3
-1
2
1
-6
6
o
x
x轴上的点,纵坐标都是0;
·
·
·
·
A
B
C
A(-4,0)
B(4,0)
O(0,0)
C(6,0)
·
·
·
D
E
F
D(0,4)
y轴上的点,横坐标都是0。
O(0,0)
E(0,-3)
F(0,-5)
O
3.写出直角坐标平面
内各点的坐标.
0
1
2
3
4
5
-4
-3
-2
-1
·
C
3
1
4
2
5
-2
-4
-1
-3
x
横轴
y
纵轴
·
B
·
A
·
D
4.描出下列各点:
A(4,3),B(-2,3),C(-4,-1),D(2,-2)
方法:先横后纵
本节课我们学面直角坐标系。学习本节我们要掌握以下三方面的内容:
1、能够正确画出直角坐标系。
2、能在直角坐标系中,根据坐标找出点,
由点求出坐标。
3、x轴上的点的纵坐标为0,表示为(x,0)
y轴上的点的横坐标为0,表示为(0,y)
课堂小结
