8.5长方体中平面与平面的位置关系的认识(第1课时) 课件(19张PPT)
文档属性
| 名称 | 8.5长方体中平面与平面的位置关系的认识(第1课时) 课件(19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-10 00:00:00 | ||
图片预览



文档简介
(共19张PPT)
2022-2023学年六年级数学下册同步精品课堂(沪教版)
第8章长方体的再认识
8.5长方体中平面与平面的位置关系的认识(第1课时)
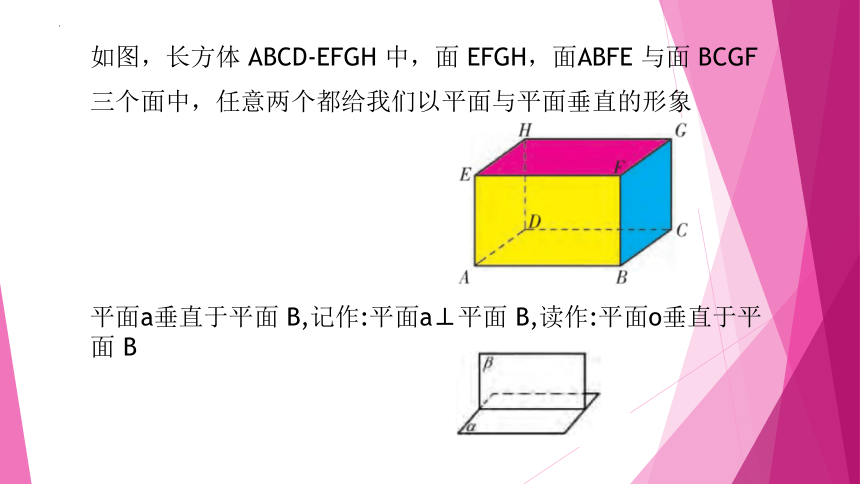
如图,长方体 ABCD-EFGH 中,面 EFGH,面ABFE 与面 BCGF 三个面中,任意两个都给我们以平面与平面垂直的形象
平面a垂直于平面 B,记作:平面a⊥平面 B,读作:平面o垂直于平面 B
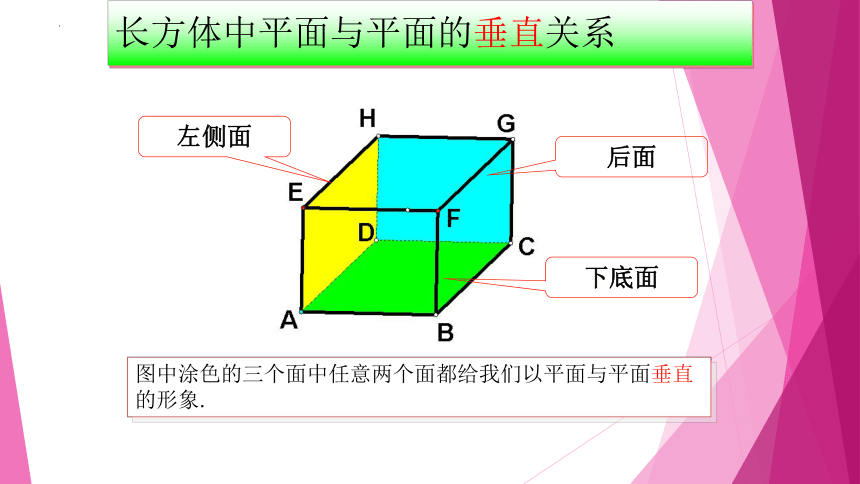
长方体中平面与平面的垂直关系
图中涂色的三个面中任意两个面都给我们以平面与平面垂直的形象.
后面
下底面
左侧面
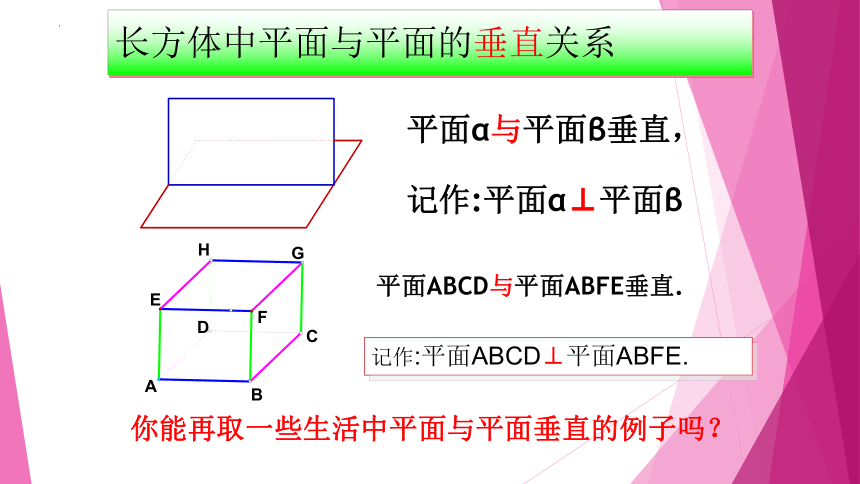
记作:平面ABCD⊥平面ABFE.
记作:平面α⊥平面β
平面α与平面β垂直,
平面ABCD与平面ABFE垂直.
长方体中平面与平面的垂直关系
你能再取一些生活中平面与平面垂直的例子吗?
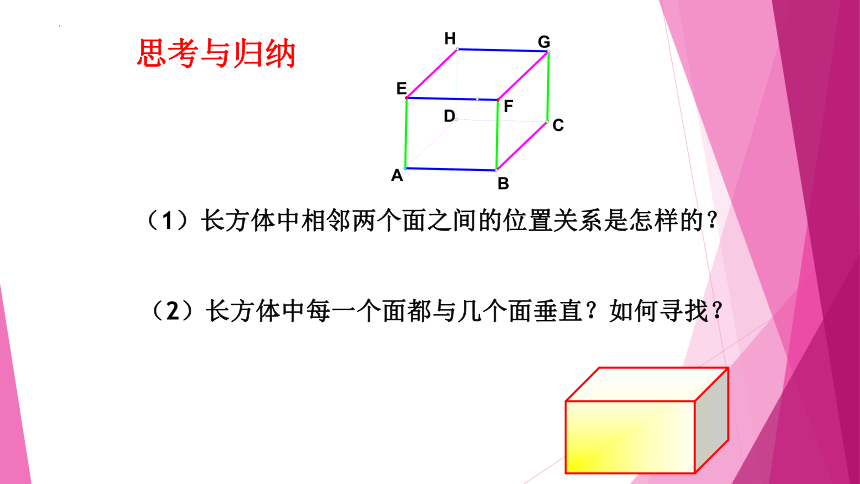
思考与归纳
(1)长方体中相邻两个面之间的位置关系是怎样的?
(2)长方体中每一个面都与几个面垂直?如何寻找?
图中粉笔盒的相邻面都瓦相垂直.
运输车的车厢顶面与四个侧面都垂直。
教室的墙面、顶面和地面中,相邻两个面互相垂直
问题 1
如何检验平面与平面垂直呢
可以用“铅垂线”检验吗
用“铅垂线”可以检验课桌的侧面是否垂直于地面,如果铅垂线能紧贴课桌的侧面,那么这个课桌的侧面就垂直于地面.
建筑工地上的工人常用铅垂线检验墙面是否垂直于水平面
也可以用“合页型折纸”检验平面与平面垂直,
用“合页型折纸”可以检验书架的隔板是否垂直于侧面.将合页型折纸直立于隔板上,如果折痕能紧贴侧面,那么隔板垂直于侧面.
在长方体ABCD-EFGH中,可以把面ADHE与面ABFE组成的图形看作是直立于面ABCD上的合页型折纸,折痕AE能紧贴面ADHE,从而说明面ADHE⊥面ABCD.
思考
可以用“三角尺”检验平面与平面垂直吗
例题 如果把右图的骰子看作是个正方体,点数1的对面是6,点数5的对面是2,点数4的对面是3,请问:
与点数是1的面垂直的面有哪些
(2) 哪些面与点数是4的面垂直
(3) 数一数这6个面中,互相垂直的面共有几对
解 (1) 与点数是1的面垂直的面为点数是2,3,4,5的面
(2) 点数是1,25,6的面与点数是4的面垂直
(3)这6个面中,互相垂直的面共有12对
1 在检验直线与平面垂直时,用了什么方法进行检验?
检验平面与平面垂直的方法
2 也可以用这三种方法检验平面与平面的垂直关系.
(1) 铅垂线;(2)合页型折纸;(3)三角尺.
(1) 铅垂线; (2)合页型折纸; (3)三角尺.
师生一起手操作,了解要点。
课本练习
1.举出几个平面与平面垂直的生活实例
2用合页型折纸检验教室的门无论开到怎样的位置,门与地面都是垂直的
3在长方体ABCD-EFGH中,写出所有垂直于平面DCGH的平面
随堂检测
1.如图:在长方体ABCD-EFGH中,
(1)与面ABCD垂直的平面是
;
(2)与面ABFE垂直的平面是
;
(3)与面BCGF垂直的平面是
;
A
B
C
E
F
G
H
D
(4)在长方体中的每一个面有 个面和它垂直。
平面ABFE、平面BCGF、平面CDHG、平面ADHE
平面ADHE、平面EFGH、平面BCGF、平面ABFE
平面ABFE、平面EFGH、平面CDHG、平面ABCD
四
2.如图:在长方体ABCD-EFGH中,
与面ABCD垂直的平面是
;
A
B
C
E
F
G
H
D
平面ABFE、平面BCGF、平面CDHG、平面ADHE
用符号语言表示为 ;
例如:平面ABCD⊥平面ABFE
1.可以用“铅垂线”检验
实际生活中如何检验平面与平面垂直呢?
用”铅垂线”可以检验课桌的侧面是否垂直于地面。如果铅垂线能紧贴课桌的侧面,那么这个课桌的侧面就垂直于地面。
课堂小结
2.可以用“合页型折纸”检验
用”合页型折纸”可以检验书架的隔板是否垂直于侧面。将合页型折纸直立于隔板上,如果折痕能紧贴侧面,
那么隔板垂直于侧面。
3.可以用“三角尺”检验
用三角尺可以检验墙面是否垂直于墙面。
如果两把三角尺各有一条直角边紧贴墙面且位置相交,另一条直角边都能紧贴另一墙面,那么墙面垂直于墙面。
2022-2023学年六年级数学下册同步精品课堂(沪教版)
第8章长方体的再认识
8.5长方体中平面与平面的位置关系的认识(第1课时)
如图,长方体 ABCD-EFGH 中,面 EFGH,面ABFE 与面 BCGF 三个面中,任意两个都给我们以平面与平面垂直的形象
平面a垂直于平面 B,记作:平面a⊥平面 B,读作:平面o垂直于平面 B
长方体中平面与平面的垂直关系
图中涂色的三个面中任意两个面都给我们以平面与平面垂直的形象.
后面
下底面
左侧面
记作:平面ABCD⊥平面ABFE.
记作:平面α⊥平面β
平面α与平面β垂直,
平面ABCD与平面ABFE垂直.
长方体中平面与平面的垂直关系
你能再取一些生活中平面与平面垂直的例子吗?
思考与归纳
(1)长方体中相邻两个面之间的位置关系是怎样的?
(2)长方体中每一个面都与几个面垂直?如何寻找?
图中粉笔盒的相邻面都瓦相垂直.
运输车的车厢顶面与四个侧面都垂直。
教室的墙面、顶面和地面中,相邻两个面互相垂直
问题 1
如何检验平面与平面垂直呢
可以用“铅垂线”检验吗
用“铅垂线”可以检验课桌的侧面是否垂直于地面,如果铅垂线能紧贴课桌的侧面,那么这个课桌的侧面就垂直于地面.
建筑工地上的工人常用铅垂线检验墙面是否垂直于水平面
也可以用“合页型折纸”检验平面与平面垂直,
用“合页型折纸”可以检验书架的隔板是否垂直于侧面.将合页型折纸直立于隔板上,如果折痕能紧贴侧面,那么隔板垂直于侧面.
在长方体ABCD-EFGH中,可以把面ADHE与面ABFE组成的图形看作是直立于面ABCD上的合页型折纸,折痕AE能紧贴面ADHE,从而说明面ADHE⊥面ABCD.
思考
可以用“三角尺”检验平面与平面垂直吗
例题 如果把右图的骰子看作是个正方体,点数1的对面是6,点数5的对面是2,点数4的对面是3,请问:
与点数是1的面垂直的面有哪些
(2) 哪些面与点数是4的面垂直
(3) 数一数这6个面中,互相垂直的面共有几对
解 (1) 与点数是1的面垂直的面为点数是2,3,4,5的面
(2) 点数是1,25,6的面与点数是4的面垂直
(3)这6个面中,互相垂直的面共有12对
1 在检验直线与平面垂直时,用了什么方法进行检验?
检验平面与平面垂直的方法
2 也可以用这三种方法检验平面与平面的垂直关系.
(1) 铅垂线;(2)合页型折纸;(3)三角尺.
(1) 铅垂线; (2)合页型折纸; (3)三角尺.
师生一起手操作,了解要点。
课本练习
1.举出几个平面与平面垂直的生活实例
2用合页型折纸检验教室的门无论开到怎样的位置,门与地面都是垂直的
3在长方体ABCD-EFGH中,写出所有垂直于平面DCGH的平面
随堂检测
1.如图:在长方体ABCD-EFGH中,
(1)与面ABCD垂直的平面是
;
(2)与面ABFE垂直的平面是
;
(3)与面BCGF垂直的平面是
;
A
B
C
E
F
G
H
D
(4)在长方体中的每一个面有 个面和它垂直。
平面ABFE、平面BCGF、平面CDHG、平面ADHE
平面ADHE、平面EFGH、平面BCGF、平面ABFE
平面ABFE、平面EFGH、平面CDHG、平面ABCD
四
2.如图:在长方体ABCD-EFGH中,
与面ABCD垂直的平面是
;
A
B
C
E
F
G
H
D
平面ABFE、平面BCGF、平面CDHG、平面ADHE
用符号语言表示为 ;
例如:平面ABCD⊥平面ABFE
1.可以用“铅垂线”检验
实际生活中如何检验平面与平面垂直呢?
用”铅垂线”可以检验课桌的侧面是否垂直于地面。如果铅垂线能紧贴课桌的侧面,那么这个课桌的侧面就垂直于地面。
课堂小结
2.可以用“合页型折纸”检验
用”合页型折纸”可以检验书架的隔板是否垂直于侧面。将合页型折纸直立于隔板上,如果折痕能紧贴侧面,
那么隔板垂直于侧面。
3.可以用“三角尺”检验
用三角尺可以检验墙面是否垂直于墙面。
如果两把三角尺各有一条直角边紧贴墙面且位置相交,另一条直角边都能紧贴另一墙面,那么墙面垂直于墙面。
