第九章 不等式与不等式组 章末复习课件(43张PPT)
文档属性
| 名称 | 第九章 不等式与不等式组 章末复习课件(43张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-10 16:41:36 | ||
图片预览







文档简介
人教版七年级下册
第九章 不等式与不等式组
1.感受生活中存在着大量的不等关系,了解不等式和一元一次不等式的意义,通过解决简单的实际问题,使学生自发地寻找不等式的解,会把不等式的解集正确地表示到数轴上;
2.经历由具体实例建立不等模型的过程,经历探究不等式解与解集的不同意义的过程,渗透数形结合思想;
3.通过对不等式、不等式解与解集的探究,引导学生在独立思考的基础上积极参与对数学问题的讨论,培养他们的合作交流意识;让学生充分体会到生活中处处有数学,并能将它们应用到生活的各个领域。
复习
目标
复习重点
重难点:一元一次不等式(组)的解法和用一元一次不等式(组)解决实际问题。
复习目标
2
知识要点
3
知识点一 不等式
㈠不等式
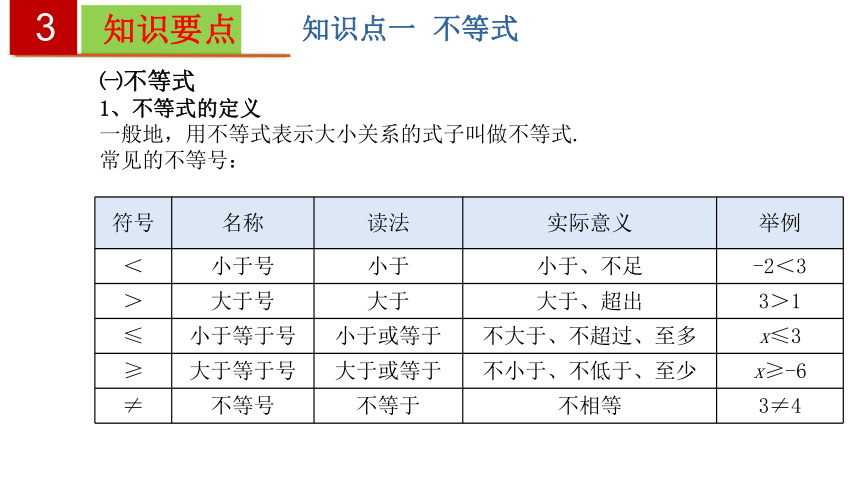
1、不等式的定义
一般地,用不等式表示大小关系的式子叫做不等式.
常见的不等号:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}符号
名称
读法
实际意义
举例
<
小于号
小于
小于、不足
-2<3
>
大于号
大于
大于、超出
3>1
≤
小于等于号
小于或等于
不大于、不超过、至多
x≤3
≥
大于等于号
大于或等于
不小于、不低于、至少
x≥-6
≠
不等号
不等于
不相等
3≠4
知识点一 不等式
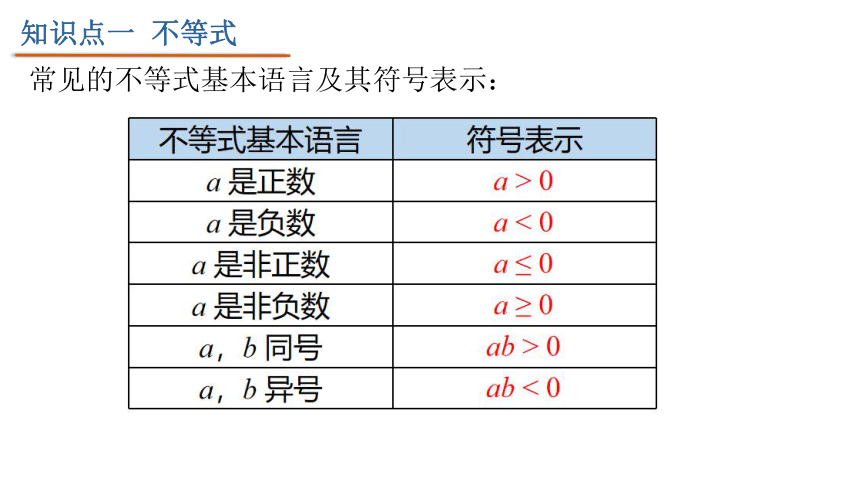
常见的不等式基本语言及其符号表示:
2、不等式的解
使不等式成立的未知数的值叫做不等式的解.
知识点一 不等式
判断一个数是不是不等式的解的方法
判断一个数是否为不等式的解,就是将这个数代替不等式中的未知数,看不等式是否成立.若成立,则该数是不等式的一个解,反之不是.
一般地,一个含有未知数的不等式的所有的解,组成这个不等式的解集.
注意!不等式的解集必须符合两个条件:
(1)解集中的每一个数值都能使不等式成立;
(2)能够使不等式成立的所有数值都在该解集中.
3、不等式的解集
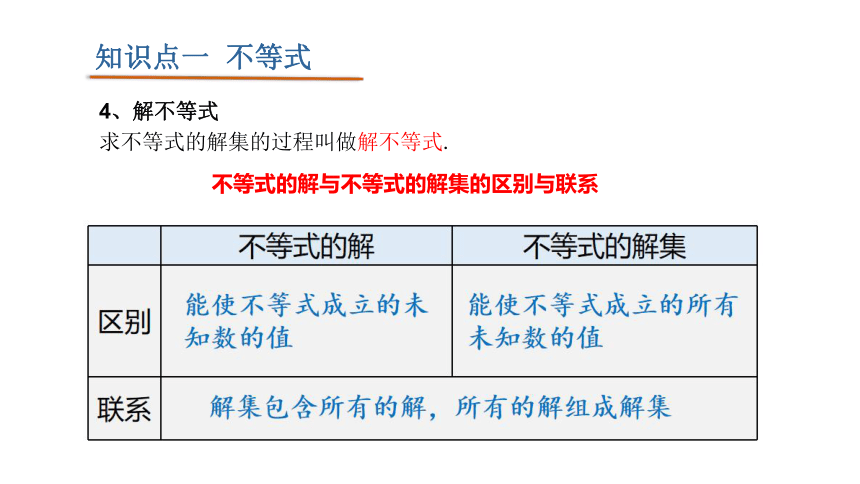
4、解不等式
求不等式的解集的过程叫做解不等式.
知识点一 不等式
不等式的解与不等式的解集的区别与联系
5、用数轴表示不等式的解集的步骤:
1.定边界点:在数轴上要标出原点和边界点,注意是实心圆点还是空心圆圈,有等号边界点画实心圆点(表示包括这一点),无等号边界点画空心圆圈(表示不包括这一点);
2.定方向:大于向右,小于向左.
知识点一 不等式
6、不等式的性质
不等式的性质1:不等式两边加(或减)同一个数(或式子),不等号的方向不变。 即如果a>b,那么a±c>b±c.
不等式的性质2:不等式两边乘(或除以)同一个正数,不等号的方向不变.
即如果a>b,c>0,那么ac>bc (或 ).
不等式的性质3:不等式两边乘(或除以)同一个负数,不等号的方向改变.
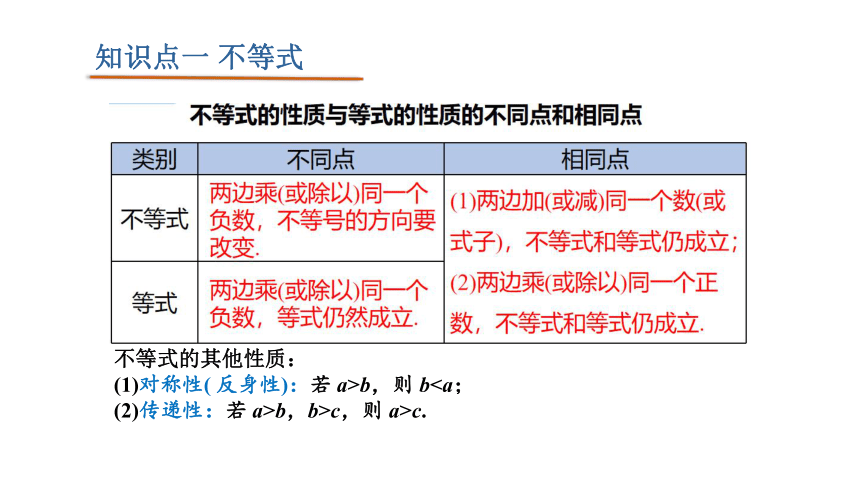
即如果a>b,c<0,那么ac知识点一 不等式
知识点一 不等式
不等式的其他性质:
(1)对称性( 反身性):若 a>b,则 b(2)传递性:若 a>b,b>c,则 a>c.
例1.判断下列式子是不是不等式:
(1) -3>0; (2) 4x+3y<0;
(3) x = 3; (4) x2+xy+y2;
(5) x+2>y+5.
解:(1) (2) (5) 是不等式;
(3) (4) 不是不等式.
【典例讲解】
例2.已知a<b,下列不等式不成立的是( )
A. a+1B. 3a<3b
C. -12a>-12b
D. 若 c<0,则 ?????????< ????????
?
D
不等式两边乘(或除以)同一个负数,不等号的方向改变.
【典例讲解】
1. 已知关于 x 的不等式 (1-a)x>2 的解集为
则 a 的取值范围是 ( )
A. a>0 B. a>1
C. a<0 D. a<1
B
【变式训练】
2.利用不等式的性质解不等式3x<2x+1,得 .?
x<1
知识要点
4
知识点二 一元一次不等式
(二)一元一次不等式
1.含有一个未知数,未知数的次数是1的不等式,叫做一元一次不等式.
一元一次不等式必须同时满足三个条件:
(1)不等式的两边都是整式;
(2)只含有一个未知数;
(3)未知数的次数是 1.
知识点二 一元一次不等式
2.解一元一次不等式步骤:
去分母 去括号 移项 合并同类项 系数化为1.
在系数化为1的这一步中,要特别注意不等式的两边都乘以(或除以)一个负数时,不等号的方向必须改变方向.
知识点二 一元一次不等式
解一元一次方程与解一元一次不等式的相同点和不同点
知识点二 一元一次不等式
3.列一元一次不等式解决实际问题的一般步骤
(1)审:弄清题意和题目中的数量关系,找出题中的不等关系,要抓住题中的关键字;
(2)设:可以直接设,也可以间接设;
(3)列:根据题目中能表示全部含义的不等关系列出不等式;
(4)解:解出所列的不等式的解集;
(5)验:检验所得结果是否正确,考虑所得的解是否符合问题的实际意义;
(6)答:写出答案.
知识点二 一元一次不等式
知识点二 一元一次不等式
(1) 2-5x < 8-6x ; (2)
解:
合并同类项,得:x < 6.
移项,得 -5x+6x < 8-2,
例3 解不等式,并把解集表示在数轴上.
不等式的解集在数轴上表示如图所示:
【典例讲解】
解:去分母,得 2(2x-1)-(9x+2)≤6,
去括号,得 4x-2-9x-2≤6,
移项,得 4x-9x≤6+2+2,
合并同类项,得 -5x≤10,
系数化 1,得 x≥-2.
不等式的解集在数轴上表示如图所示.
(2)
【典例讲解】
例4. 若关于x的方程 的解是非负数,求m的取值范围。
解:由
,得
例5.倡导健康生活,推进全民健身.某社区要购进A,B两种型号的健身器材若干套,A,B两种型号健身器材的购买单价分别为每套280元,430元,且每种型号健身器材必须整套购买.若购买A,B两种型号的健身器材共50套,且支出不超过16 000元,A种型号健身器材至少要购买多少套?
【典例讲解】
3(1)求不等式 3x+1≥4x-5的正整数解.
移项得:
合并同类项得:
化系数为1得:
解:
3x﹣4x≥-5-1
﹣x ≥-6
x≤6
所以不等式 的正整数解为:1、2、3、4、5、6
【变式训练】
8x-4≥15x-60
8x-15x≥-60+4
-7x≥-56
x≤8
去分母得:
去括号得:
移项得:
合并同类项得:
化系数为1得:
解:
同乘最简公分母12,方向不变
同除以-7,方向改变
0
1
2
-1
3
4
5
6
7
8
解:解不等式 x+m<1,得 x<1-m.
根据题意得 3<1-m≤4,
即 -3≤m<-2.
4. 若关于 x 的不等式 x+m<1 只有 3 个正整数解,则 m 的取值范围是___________.
-3≤m<-2
分析:关于 x 的不等式只有 3 个正整数解
x 的上限 1 - m 在 3 与 4 之间
【变式训练】
5.某服装店计划购进一批甲、乙两种款式的运动服进行销售,进价和售价如下表所示:
若购进两种款式的运动服共300套,且投入资金不超过26 800元.
【变式训练】
该服装店应至少购进甲款运动服多少套?
知识要点
5
知识点三 一元一次不等式组
(三)一元一次不等式组
1.一元一次不等式组的定义:类似于方程组,把几个含有相同未知数的一元一次不等式合起来,就组成一个一元一次不等式组.
一元一次不等式组必须同时满足三个条件:
①每个不等式都是一元一次不等式;
②含有同一个未知数;
③不等式的个数不少于2.
知识要点
5
知识点三 一元一次不等式组
注意!
“公共部分”是指同时满足不等式组中每一个不等式的解集的部分.如果组成不等式组的各个不等式的解集没有公共部分,则这个不等式组无解.
2.一元一次不等式组的解集
一般地,几个不等式的解集的公共部分,叫做由它们所组成的不等式组的解集.
确定一元一次不等式组的解集的两种方法
(1)数轴法:即先把不等式组中每个不等式的解集在数轴上表示出来,找出它们的公共部分,就得到不等式组的解集,若无公共部分,则不等式组无解;
(2)口诀法:同大取大,同小取小,大大小小无处找,大小小大中间找.
一元一次不等式组的解集有四种情况:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}不等式组
(a>b>0)
不等式组的解集
不等式组的解集在数轴上的表示
巧记口诀
x>a
x无解
b同大取大
同小取小
大大小小无处找
大小小大中间找
b
0
a
b
0
a
b
0
a
b
0
a
3、一元一次不等式组的步骤:
(1)先分别解不等式组中的每一个不等式,分别求出它们的解集;
(2)将每个不等式的解集在同一条数轴上表示出来,找出它们的公共部分,注意:公共部分可能没有,也可能是一个点;
(3)根据公共部分写出不等式组的解集,若没有公共部分,则说明不等式组无解。
特别注意:用数轴表示不等式的解集时,<、>用空心,≤、≥用实心。 >、≥向右画,<、≤向左画。
知识要点
5
知识点三 一元一次不等式组
4.不等式(组)在实际生活中的应用
当应用题中出现以下的关键词,如大,小,多,少,不小于,不大于,至少,至多等,应属列不等式(组)来解决的问题,而不能列方程(组)来解.
5.列一元一次不等式组解应用题的一般步骤:
1、审:审清题意,弄懂已知什么,求什么,以及各个数量之间的关系。
2、设:只能设一个未知数,一般是与所求问题有直接关系的量。
3、找:找出题中所有的不等关系,特别是隐含的数量关系。
4、列:列出不等式组。
5、解:分别解出每个不等式的解集,再求其公共部分,得出结果。
6、答:根据所得结果作出回答。
例6 解不等式组 把解集在数轴上表示出来,并将解集中的整数解写出来.
?
?
解:解不等式?,得 x≤3.
解不等式?,得
所以这个不等式组的解集是 ,解集在数轴上表示如下:
通过观察数轴可知该不等式组的整数解为 2,3.
2
3
1
0
4
2
3
【典例讲解】
例7.若关于 x 的不等式组 有解,求
实数 a 的值.
解:
解不等式①得 x<a - 1.
解不等式②得 x>-6.
∵ 不等式组有解,
∴ -6<a - 1.
∴ a>-5.
【典例讲解】
例8.某服装厂现有 A 种布料 70 m,B 种布料 52 m,现计划用这两种布料生产 M,N 两种型号的时装共 80 套,已知做一套 M 型号的时装需用 A 种布料 0.6 m,B 种布料0.9 m,可获得利润 45 元;做一套 N 型号的时装需用 A种布料 1.1 m,B 种布料 0.4 m,可获得利润 50 元. 该服装厂在生产这批时装时,当生产 N 型号的时装多少套时,所获得的利润最大?最大利润为多少?
解:设生产 N 型号的时装 x 套,
由题意得 0.680?????+1.1????≤70,0.980?????+0.4????≤52,
解得 40≤x≤44.
?
x
80-x
A:0.6(80-x)
B:0.9(80-x)
A:1.1x
B:0.4x
【典例讲解】
由题意得获得的利润为 y=50x+45×(80-x),
当 x=40时,y=3800;
当 x=41时,y=3805;
当 x=42时,y=3810;
当 x=43时,y=3815;
当 x=44时,y=3820.
故当生产 N 型号的时装 44 套时,所获得的利润最大,最大利润为 3820 元.
6.解不等式组:?????4≤2?????1,①12????+3>????+1.②
?
解:解不等式①,得 x≥-2.
解不等式②,得 x<1.
把不等式①和②的解集在数轴上表示出来,如下图所示.
2
0
-3
-2
-1
1
3
由图可得不等式组的解集为 -2≤x<1.
【变式训练】
7.已知不等式组 ?????????≥0,?2????>?4 有解,则 a 的取值范围为( )
A. a>-2 B. a≥-2 C. a<2 D. a≥2
?
C
x≥a
x<2
8.若关于 x 的不等式组 ?????????<0,7?2????≤1 的整数解共有 3 个,则 m 的取值范围是( )
A.5B.5C.5≤m≤6
D.6?
xx≥3
不等式组的解集 3≤x3,4,5
B
【变式训练】
5.为了抓住梵净山文化艺术节的商机,某商店决定购进A、B两种艺术节纪念品.若购进A种纪念品8件,B种纪念品3件,需要950元;若购进A种纪念品5件,B种纪念品6件,需要800元.
(1)求购进A、B两种纪念品每件各需多少元?
【变式训练】
解:(1)设该商店购进一件A种纪念品需要a元,购进一件B种纪念品需要b元,根据题意得方程组得:
解方程组得:
∴购进一件A种纪念品需要100元,购进一件B种纪念品需要50元;
(2)若该商店决定购进这两种纪念品共100件,考虑市场需求和资金周转,用于购买这100件纪念品的资金不少于7500元,但不超过7650元,那么该商店共有几种进货方案?
【变式训练】
(2)设该商店购进A种纪念品x个,则购进B种纪念品有(100﹣x)个,
解得:50≤x≤53,
∵x 为正整数,
∴共有4种进货方案;
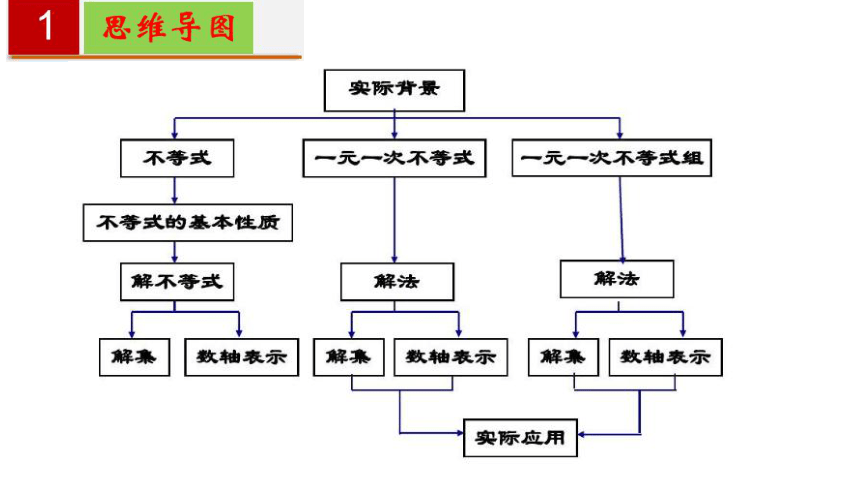
一元一次不等式(组)
不等式
不等式的解集
一元一次不等式
一元一次不等式组
解集
数轴表示
不等式的基本性质
解 集
数轴表示
解法
解法
实际应用
第九章 不等式与不等式组
1.感受生活中存在着大量的不等关系,了解不等式和一元一次不等式的意义,通过解决简单的实际问题,使学生自发地寻找不等式的解,会把不等式的解集正确地表示到数轴上;
2.经历由具体实例建立不等模型的过程,经历探究不等式解与解集的不同意义的过程,渗透数形结合思想;
3.通过对不等式、不等式解与解集的探究,引导学生在独立思考的基础上积极参与对数学问题的讨论,培养他们的合作交流意识;让学生充分体会到生活中处处有数学,并能将它们应用到生活的各个领域。
复习
目标
复习重点
重难点:一元一次不等式(组)的解法和用一元一次不等式(组)解决实际问题。
复习目标
2
知识要点
3
知识点一 不等式
㈠不等式
1、不等式的定义
一般地,用不等式表示大小关系的式子叫做不等式.
常见的不等号:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}符号
名称
读法
实际意义
举例
<
小于号
小于
小于、不足
-2<3
>
大于号
大于
大于、超出
3>1
≤
小于等于号
小于或等于
不大于、不超过、至多
x≤3
≥
大于等于号
大于或等于
不小于、不低于、至少
x≥-6
≠
不等号
不等于
不相等
3≠4
知识点一 不等式
常见的不等式基本语言及其符号表示:
2、不等式的解
使不等式成立的未知数的值叫做不等式的解.
知识点一 不等式
判断一个数是不是不等式的解的方法
判断一个数是否为不等式的解,就是将这个数代替不等式中的未知数,看不等式是否成立.若成立,则该数是不等式的一个解,反之不是.
一般地,一个含有未知数的不等式的所有的解,组成这个不等式的解集.
注意!不等式的解集必须符合两个条件:
(1)解集中的每一个数值都能使不等式成立;
(2)能够使不等式成立的所有数值都在该解集中.
3、不等式的解集
4、解不等式
求不等式的解集的过程叫做解不等式.
知识点一 不等式
不等式的解与不等式的解集的区别与联系
5、用数轴表示不等式的解集的步骤:
1.定边界点:在数轴上要标出原点和边界点,注意是实心圆点还是空心圆圈,有等号边界点画实心圆点(表示包括这一点),无等号边界点画空心圆圈(表示不包括这一点);
2.定方向:大于向右,小于向左.
知识点一 不等式
6、不等式的性质
不等式的性质1:不等式两边加(或减)同一个数(或式子),不等号的方向不变。 即如果a>b,那么a±c>b±c.
不等式的性质2:不等式两边乘(或除以)同一个正数,不等号的方向不变.
即如果a>b,c>0,那么ac>bc (或 ).
不等式的性质3:不等式两边乘(或除以)同一个负数,不等号的方向改变.
即如果a>b,c<0,那么ac
知识点一 不等式
不等式的其他性质:
(1)对称性( 反身性):若 a>b,则 b
例1.判断下列式子是不是不等式:
(1) -3>0; (2) 4x+3y<0;
(3) x = 3; (4) x2+xy+y2;
(5) x+2>y+5.
解:(1) (2) (5) 是不等式;
(3) (4) 不是不等式.
【典例讲解】
例2.已知a<b,下列不等式不成立的是( )
A. a+1
C. -12a>-12b
D. 若 c<0,则 ?????????< ????????
?
D
不等式两边乘(或除以)同一个负数,不等号的方向改变.
【典例讲解】
1. 已知关于 x 的不等式 (1-a)x>2 的解集为
则 a 的取值范围是 ( )
A. a>0 B. a>1
C. a<0 D. a<1
B
【变式训练】
2.利用不等式的性质解不等式3x<2x+1,得 .?
x<1
知识要点
4
知识点二 一元一次不等式
(二)一元一次不等式
1.含有一个未知数,未知数的次数是1的不等式,叫做一元一次不等式.
一元一次不等式必须同时满足三个条件:
(1)不等式的两边都是整式;
(2)只含有一个未知数;
(3)未知数的次数是 1.
知识点二 一元一次不等式
2.解一元一次不等式步骤:
去分母 去括号 移项 合并同类项 系数化为1.
在系数化为1的这一步中,要特别注意不等式的两边都乘以(或除以)一个负数时,不等号的方向必须改变方向.
知识点二 一元一次不等式
解一元一次方程与解一元一次不等式的相同点和不同点
知识点二 一元一次不等式
3.列一元一次不等式解决实际问题的一般步骤
(1)审:弄清题意和题目中的数量关系,找出题中的不等关系,要抓住题中的关键字;
(2)设:可以直接设,也可以间接设;
(3)列:根据题目中能表示全部含义的不等关系列出不等式;
(4)解:解出所列的不等式的解集;
(5)验:检验所得结果是否正确,考虑所得的解是否符合问题的实际意义;
(6)答:写出答案.
知识点二 一元一次不等式
知识点二 一元一次不等式
(1) 2-5x < 8-6x ; (2)
解:
合并同类项,得:x < 6.
移项,得 -5x+6x < 8-2,
例3 解不等式,并把解集表示在数轴上.
不等式的解集在数轴上表示如图所示:
【典例讲解】
解:去分母,得 2(2x-1)-(9x+2)≤6,
去括号,得 4x-2-9x-2≤6,
移项,得 4x-9x≤6+2+2,
合并同类项,得 -5x≤10,
系数化 1,得 x≥-2.
不等式的解集在数轴上表示如图所示.
(2)
【典例讲解】
例4. 若关于x的方程 的解是非负数,求m的取值范围。
解:由
,得
例5.倡导健康生活,推进全民健身.某社区要购进A,B两种型号的健身器材若干套,A,B两种型号健身器材的购买单价分别为每套280元,430元,且每种型号健身器材必须整套购买.若购买A,B两种型号的健身器材共50套,且支出不超过16 000元,A种型号健身器材至少要购买多少套?
【典例讲解】
3(1)求不等式 3x+1≥4x-5的正整数解.
移项得:
合并同类项得:
化系数为1得:
解:
3x﹣4x≥-5-1
﹣x ≥-6
x≤6
所以不等式 的正整数解为:1、2、3、4、5、6
【变式训练】
8x-4≥15x-60
8x-15x≥-60+4
-7x≥-56
x≤8
去分母得:
去括号得:
移项得:
合并同类项得:
化系数为1得:
解:
同乘最简公分母12,方向不变
同除以-7,方向改变
0
1
2
-1
3
4
5
6
7
8
解:解不等式 x+m<1,得 x<1-m.
根据题意得 3<1-m≤4,
即 -3≤m<-2.
4. 若关于 x 的不等式 x+m<1 只有 3 个正整数解,则 m 的取值范围是___________.
-3≤m<-2
分析:关于 x 的不等式只有 3 个正整数解
x 的上限 1 - m 在 3 与 4 之间
【变式训练】
5.某服装店计划购进一批甲、乙两种款式的运动服进行销售,进价和售价如下表所示:
若购进两种款式的运动服共300套,且投入资金不超过26 800元.
【变式训练】
该服装店应至少购进甲款运动服多少套?
知识要点
5
知识点三 一元一次不等式组
(三)一元一次不等式组
1.一元一次不等式组的定义:类似于方程组,把几个含有相同未知数的一元一次不等式合起来,就组成一个一元一次不等式组.
一元一次不等式组必须同时满足三个条件:
①每个不等式都是一元一次不等式;
②含有同一个未知数;
③不等式的个数不少于2.
知识要点
5
知识点三 一元一次不等式组
注意!
“公共部分”是指同时满足不等式组中每一个不等式的解集的部分.如果组成不等式组的各个不等式的解集没有公共部分,则这个不等式组无解.
2.一元一次不等式组的解集
一般地,几个不等式的解集的公共部分,叫做由它们所组成的不等式组的解集.
确定一元一次不等式组的解集的两种方法
(1)数轴法:即先把不等式组中每个不等式的解集在数轴上表示出来,找出它们的公共部分,就得到不等式组的解集,若无公共部分,则不等式组无解;
(2)口诀法:同大取大,同小取小,大大小小无处找,大小小大中间找.
一元一次不等式组的解集有四种情况:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}不等式组
(a>b>0)
不等式组的解集
不等式组的解集在数轴上的表示
巧记口诀
x>a
x无解
b
同小取小
大大小小无处找
大小小大中间找
b
0
a
b
0
a
b
0
a
b
0
a
3、一元一次不等式组的步骤:
(1)先分别解不等式组中的每一个不等式,分别求出它们的解集;
(2)将每个不等式的解集在同一条数轴上表示出来,找出它们的公共部分,注意:公共部分可能没有,也可能是一个点;
(3)根据公共部分写出不等式组的解集,若没有公共部分,则说明不等式组无解。
特别注意:用数轴表示不等式的解集时,<、>用空心,≤、≥用实心。 >、≥向右画,<、≤向左画。
知识要点
5
知识点三 一元一次不等式组
4.不等式(组)在实际生活中的应用
当应用题中出现以下的关键词,如大,小,多,少,不小于,不大于,至少,至多等,应属列不等式(组)来解决的问题,而不能列方程(组)来解.
5.列一元一次不等式组解应用题的一般步骤:
1、审:审清题意,弄懂已知什么,求什么,以及各个数量之间的关系。
2、设:只能设一个未知数,一般是与所求问题有直接关系的量。
3、找:找出题中所有的不等关系,特别是隐含的数量关系。
4、列:列出不等式组。
5、解:分别解出每个不等式的解集,再求其公共部分,得出结果。
6、答:根据所得结果作出回答。
例6 解不等式组 把解集在数轴上表示出来,并将解集中的整数解写出来.
?
?
解:解不等式?,得 x≤3.
解不等式?,得
所以这个不等式组的解集是 ,解集在数轴上表示如下:
通过观察数轴可知该不等式组的整数解为 2,3.
2
3
1
0
4
2
3
【典例讲解】
例7.若关于 x 的不等式组 有解,求
实数 a 的值.
解:
解不等式①得 x<a - 1.
解不等式②得 x>-6.
∵ 不等式组有解,
∴ -6<a - 1.
∴ a>-5.
【典例讲解】
例8.某服装厂现有 A 种布料 70 m,B 种布料 52 m,现计划用这两种布料生产 M,N 两种型号的时装共 80 套,已知做一套 M 型号的时装需用 A 种布料 0.6 m,B 种布料0.9 m,可获得利润 45 元;做一套 N 型号的时装需用 A种布料 1.1 m,B 种布料 0.4 m,可获得利润 50 元. 该服装厂在生产这批时装时,当生产 N 型号的时装多少套时,所获得的利润最大?最大利润为多少?
解:设生产 N 型号的时装 x 套,
由题意得 0.680?????+1.1????≤70,0.980?????+0.4????≤52,
解得 40≤x≤44.
?
x
80-x
A:0.6(80-x)
B:0.9(80-x)
A:1.1x
B:0.4x
【典例讲解】
由题意得获得的利润为 y=50x+45×(80-x),
当 x=40时,y=3800;
当 x=41时,y=3805;
当 x=42时,y=3810;
当 x=43时,y=3815;
当 x=44时,y=3820.
故当生产 N 型号的时装 44 套时,所获得的利润最大,最大利润为 3820 元.
6.解不等式组:?????4≤2?????1,①12????+3>????+1.②
?
解:解不等式①,得 x≥-2.
解不等式②,得 x<1.
把不等式①和②的解集在数轴上表示出来,如下图所示.
2
0
-3
-2
-1
1
3
由图可得不等式组的解集为 -2≤x<1.
【变式训练】
7.已知不等式组 ?????????≥0,?2????>?4 有解,则 a 的取值范围为( )
A. a>-2 B. a≥-2 C. a<2 D. a≥2
?
C
x≥a
x<2
8.若关于 x 的不等式组 ?????????<0,7?2????≤1 的整数解共有 3 个,则 m 的取值范围是( )
A.5
D.6
x
不等式组的解集 3≤x
B
【变式训练】
5.为了抓住梵净山文化艺术节的商机,某商店决定购进A、B两种艺术节纪念品.若购进A种纪念品8件,B种纪念品3件,需要950元;若购进A种纪念品5件,B种纪念品6件,需要800元.
(1)求购进A、B两种纪念品每件各需多少元?
【变式训练】
解:(1)设该商店购进一件A种纪念品需要a元,购进一件B种纪念品需要b元,根据题意得方程组得:
解方程组得:
∴购进一件A种纪念品需要100元,购进一件B种纪念品需要50元;
(2)若该商店决定购进这两种纪念品共100件,考虑市场需求和资金周转,用于购买这100件纪念品的资金不少于7500元,但不超过7650元,那么该商店共有几种进货方案?
【变式训练】
(2)设该商店购进A种纪念品x个,则购进B种纪念品有(100﹣x)个,
解得:50≤x≤53,
∵x 为正整数,
∴共有4种进货方案;
一元一次不等式(组)
不等式
不等式的解集
一元一次不等式
一元一次不等式组
解集
数轴表示
不等式的基本性质
解 集
数轴表示
解法
解法
实际应用
