湖北省巴东县2022-2023学年九年级下册数学期中考试题(含答案)
文档属性
| 名称 | 湖北省巴东县2022-2023学年九年级下册数学期中考试题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 669.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-10 20:44:08 | ||
图片预览

文档简介
2023年春季学期期中教学质量监测
九年级数学试题卷
范围:九年级数学人教版上下册 考时:120分钟 满分:120分
注意事项:
1.本试卷分试题卷和答题卷两个部分。
2.答题前,请你务必将自己的姓名、准考证号填写在试题卷上,并填写答题卷上的考生信息。
3.选择题务必使用2B铅笔在答题卷选择题的答题区域内填涂;非选择题务必使用黑色签字笔在答题卷非选择题各题指定的答题区域内作答。填涂、书写在试题卷上的一律无效。
4.考试结束,试题卷、答题卷一并上交。
一、选择题(每小题3分,共36分)
1.如图所示的几何体是由 6 个完全相同的小立方块搭成,则这个几何体的左视图是(▲)
A. B. C. D.
2.已知x=2是一元二次方程x2+bx-b=0的解,则b=(▲)
A. -2 B.-4 C.0 D.4
3.抛物线y=-x2+3x-的对称轴是(▲)
A.x=6 B.x=-3 C.x=- D.x=3
4.下面图形中既是轴对称图形又是中心对称图形的是(▲)
A. B. C. D.
科克曲线 笛卡尔心形线 阿基米德螺旋线 赵爽弦图
5.扇子最早称“翣”,在我国已有两千多年历史.“打开半个月亮,收起兜里可装,来时荷花初放,去时菊花正黄.”这则谜语说的就是扇子. 如图,一竹扇完全打开后,外侧两竹条AB,AC夹角为135°,AB的长为30cm, 扇面BD
的长为20cm,则扇面面积为(▲)cm2
A.π B.600π C.300π D.30π
6.动物学家通过大量的调查估计,某种动物活到20岁的概率为0.8,活到25岁的概率为0.5,那么,现年20岁的这种动物活到25岁的概率是(▲)
A.0 B.1 C. D.
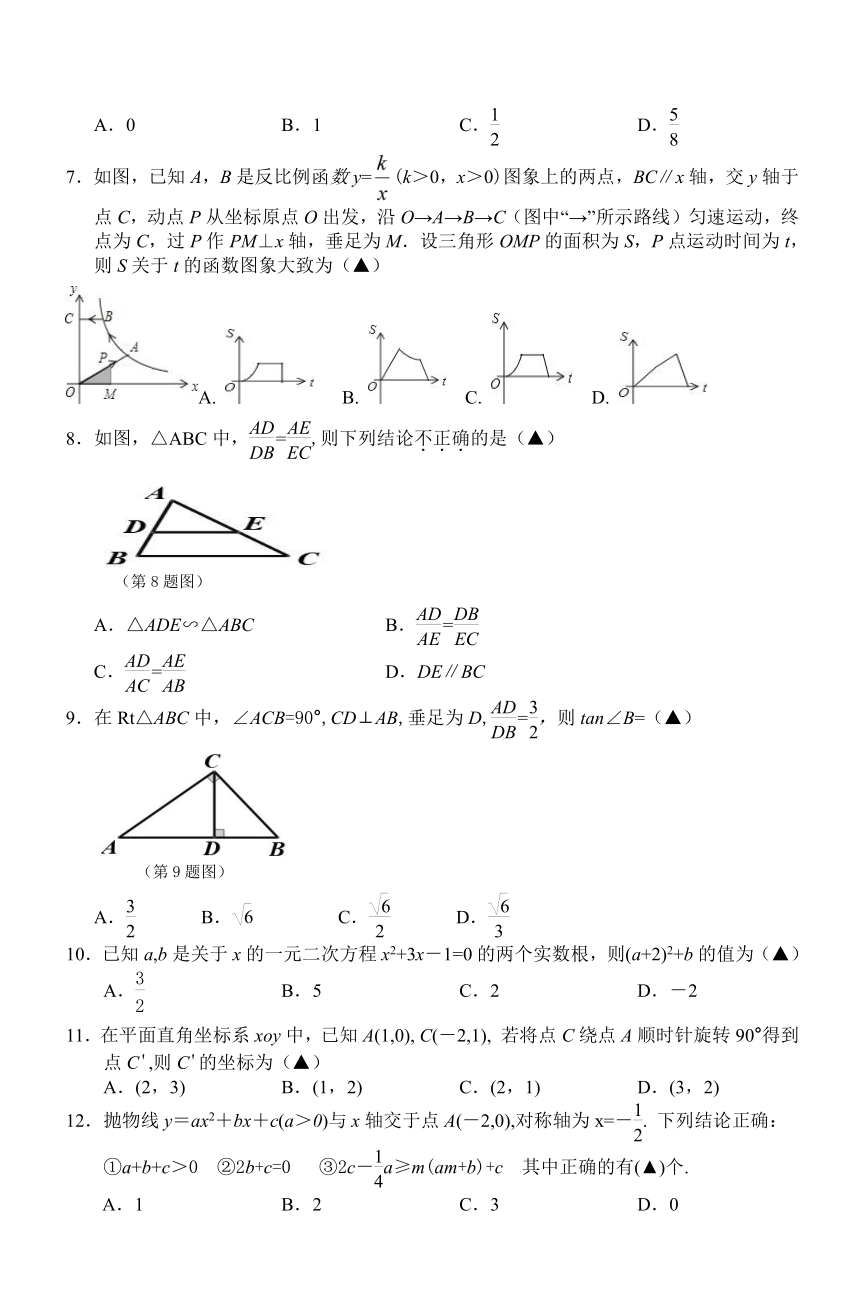
7.如图,已知A,B是反比例函数y=(k>0,x>0)图象上的两点,BC∥x轴,交y轴于点C,动点P从坐标原点O出发,沿O→A→B→C(图中“→”所示路线)匀速运动,终点为C,过P作PM⊥x轴,垂足为M.设三角形OMP的面积为S,P点运动时间为t,则S关于t的函数图象大致为(▲)
A. B. C. D.
8.如图,△ABC中,=,则下列结论不正确的是(▲)
A.△ADE∽△ABC B.=
C.= D.DE∥BC
9.在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,=,则tan∠B=(▲)
A. B. C. D.
10.已知a,b是关于x的一元二次方程x2+3x-1=0的两个实数根,则(a+2)2+b的值为(▲)
A. B.5 C.2 D.-2
11.在平面直角坐标系xoy中,已知A(1,0), C(-2,1), 若将点C绕点A顺时针旋转90°得到点C',则C'的坐标为(▲)
A.(2,3) B.(1,2) C.(2,1) D.(3,2)
12.抛物线y=ax2+bx+c(a>0)与x轴交于点A(-2,0),对称轴为x=-. 下列结论正确:
①a+b+c>0 ②2b+c=0 ③2c-a≥m(am+b)+c 其中正确的有(▲)个.
A.1 B.2 C.3 D.0
二、填空题(每小题3分,共计12分)
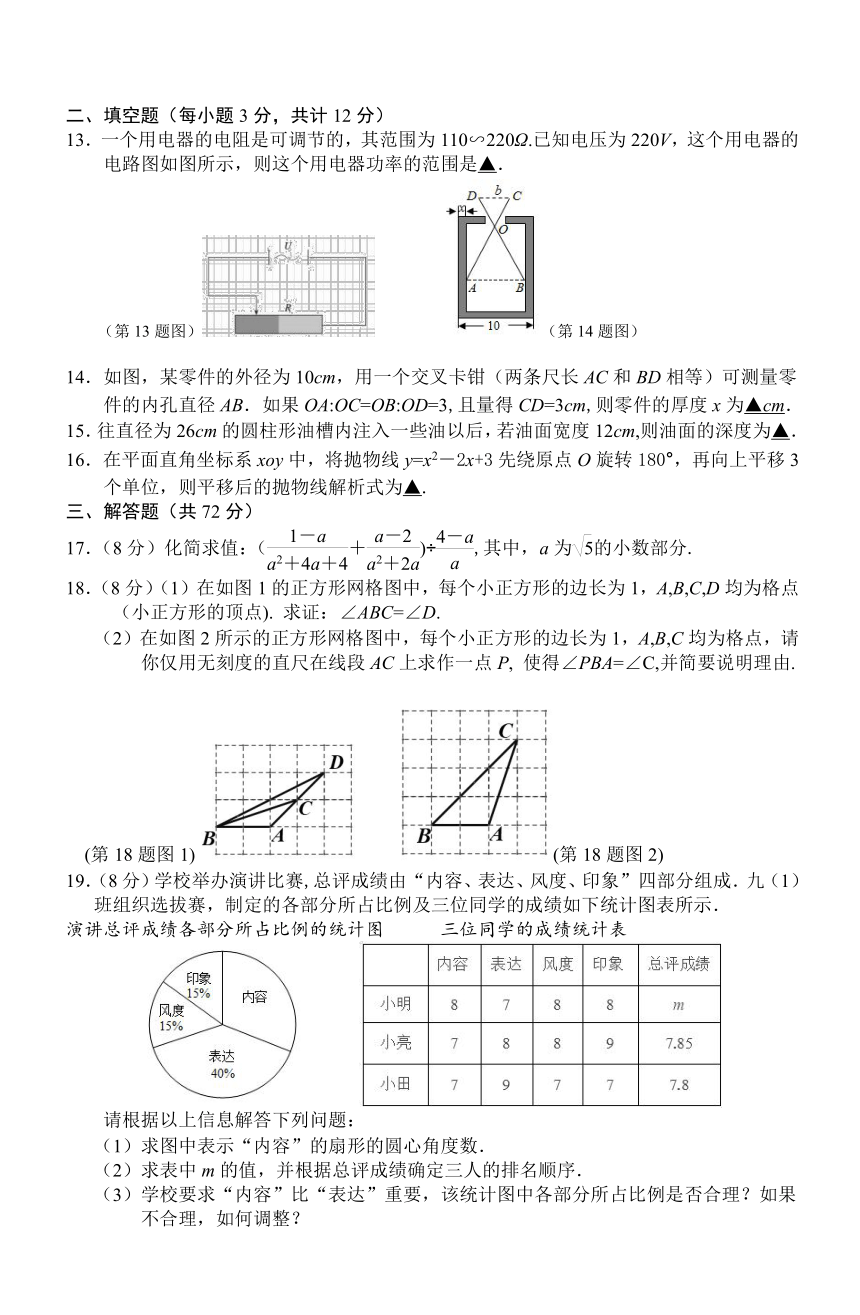
13.一个用电器的电阻是可调节的,其范围为110∽220Ω.已知电压为220V,这个用电器的电路图如图所示,则这个用电器功率的范围是▲.
(第13题图) (第14题图)
14.如图,某零件的外径为10cm,用一个交叉卡钳(两条尺长AC和BD相等)可测量零件的内孔直径AB.如果OA:OC=OB:OD=3,且量得CD=3cm,则零件的厚度x为▲cm.
15.往直径为26cm的圆柱形油槽内注入一些油以后,若油面宽度12cm,则油面的深度为▲.
16.在平面直角坐标系xoy中,将抛物线y=x2-2x+3先绕原点O旋转180°,再向上平移3个单位,则平移后的抛物线解析式为▲.
三、解答题(共72分)
17.(8分)化简求值:(+)÷,其中,a为的小数部分.
18.(8分)(1)在如图1的正方形网格图中,每个小正方形的边长为1,A,B,C,D均为格点(小正方形的顶点). 求证:∠ABC=∠D.
(2)在如图2所示的正方形网格图中,每个小正方形的边长为1,A,B,C均为格点,请你仅用无刻度的直尺在线段AC上求作一点P, 使得∠PBA=∠C,并简要说明理由.
(第18题图1) (第18题图2)
19.(8分)学校举办演讲比赛,总评成绩由“内容、表达、风度、印象”四部分组成.九(1)班组织选拔赛,制定的各部分所占比例及三位同学的成绩如下统计图表所示.
演讲总评成绩各部分所占比例的统计图 三位同学的成绩统计表
请根据以上信息解答下列问题:
(1)求图中表示“内容”的扇形的圆心角度数.
(2)求表中m的值,并根据总评成绩确定三人的排名顺序.
(3)学校要求“内容”比“表达”重要,该统计图中各部分所占比例是否合理?如果不合理,如何调整?
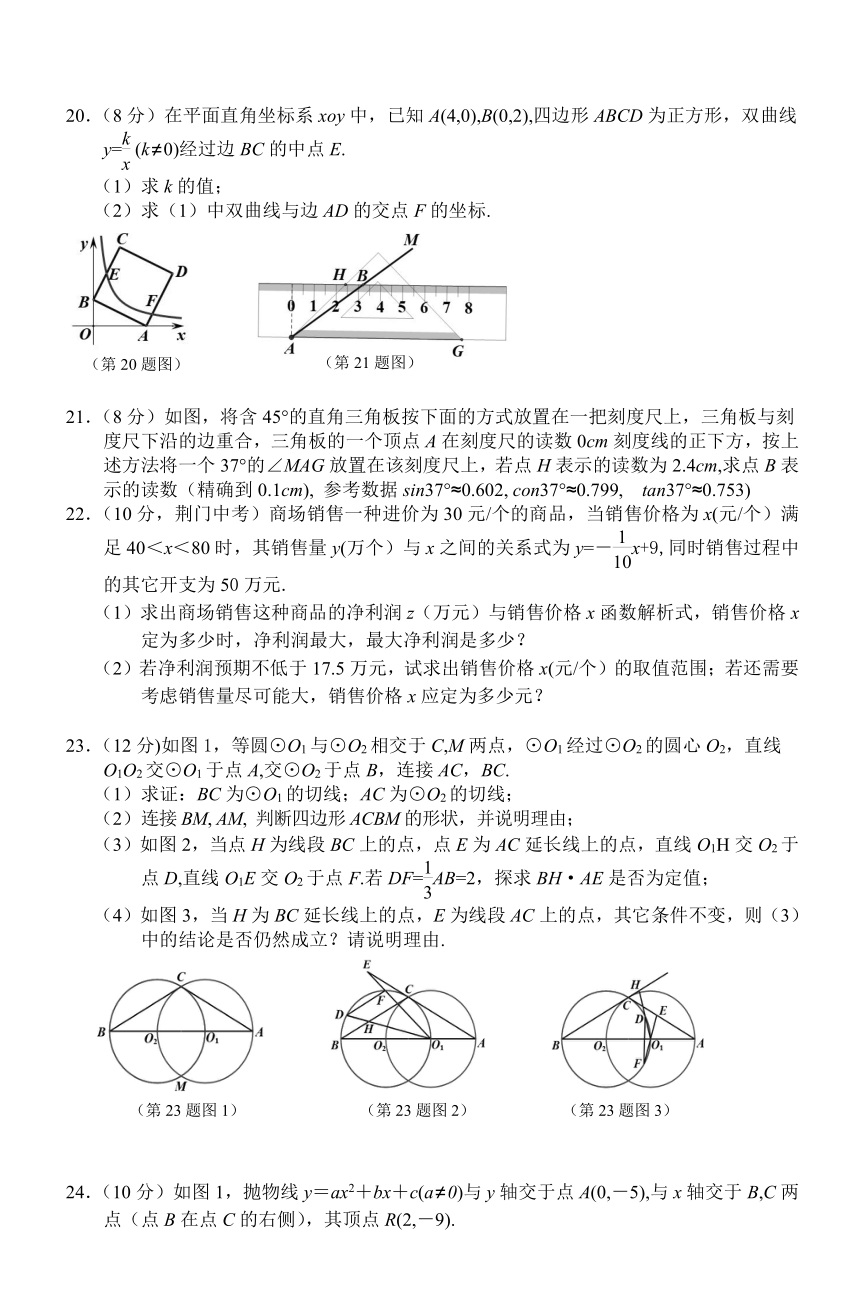
20.(8分)在平面直角坐标系xoy中,已知A(4,0),B(0,2),四边形ABCD为正方形,双曲线y= (k≠0)经过边BC的中点E.
(1)求k的值;
(2)求(1)中双曲线与边AD的交点F的坐标.
21.(8分)如图,将含45°的直角三角板按下面的方式放置在一把刻度尺上,三角板与刻度尺下沿的边重合,三角板的一个顶点A在刻度尺的读数0cm刻度线的正下方,按上述方法将一个37°的∠MAG放置在该刻度尺上,若点H表示的读数为2.4cm,求点B表示的读数(精确到0.1cm), 参考数据sin37°≈0.602, con37°≈0.799, tan37°≈0.753)
22.(10分,荆门中考)商场销售一种进价为30元/个的商品,当销售价格为x(元/个)满足40<x<80时,其销售量y(万个)与x之间的关系式为y=-x+9,同时销售过程中的其它开支为50万元.
(1)求出商场销售这种商品的净利润z(万元)与销售价格x函数解析式,销售价格x定为多少时,净利润最大,最大净利润是多少?
(2)若净利润预期不低于17.5万元,试求出销售价格x(元/个)的取值范围;若还需要考虑销售量尽可能大,销售价格x应定为多少元?
23.(12分)如图1,等圆⊙O1与⊙O2相交于C,M两点,⊙O1经过⊙O2的圆心O2,直线O1O2交⊙O1于点A,交⊙O2于点B,连接AC,BC.
(1)求证:BC为⊙O1的切线;AC为⊙O2的切线;
(2)连接BM, AM, 判断四边形ACBM的形状,并说明理由;
(3)如图2,当点H为线段BC上的点,点E为AC延长线上的点,直线O1H交O2于点D,直线O1E交O2于点F.若DF=AB=2,探求BH·AE是否为定值;
(4)如图3,当H为BC延长线上的点,E为线段AC上的点,其它条件不变,则(3)中的结论是否仍然成立?请说明理由.
24.(10分)如图1,抛物线y=ax2+bx+c(a≠0)与y轴交于点A(0,-5),与x轴交于B,C两点(点B在点C的右侧),其顶点R(2,-9).
(1)求抛物线解析式(直接写出结果);
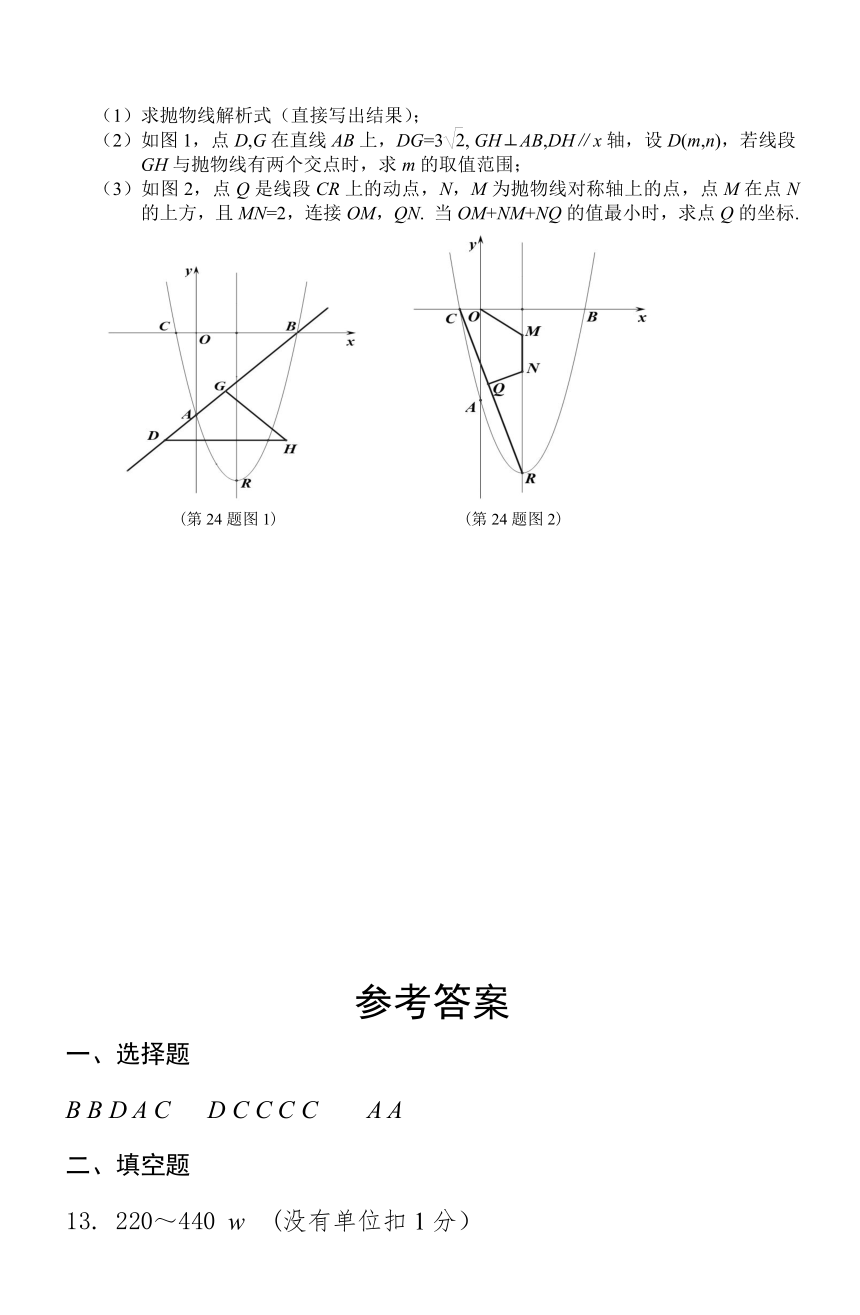
(2)如图1,点D,G在直线AB上,DG=3, GH⊥AB,DH∥x轴,设D(m,n),若线段GH与抛物线有两个交点时,求m的取值范围;
(3)如图2,点Q是线段CR上的动点,N,M为抛物线对称轴上的点,点M在点N的上方,且MN=2,连接OM,QN. 当OM+NM+NQ的值最小时,求点Q的坐标.
(第24题图1) (第24题图2)
参考答案
一、选择题
B B D A C D C C C C A A
二、填空题
13. 220~440 w (没有单位扣1分)
14.
15.13- cm或13+ cm (没有单位扣1分)
16.y=-x2-2x
三、解答题
17.解: 原式=-……………(5分)
a为的小数部分,则a=-2 …………(6分)
原式=- …………(8分)
18.(1)证明:略…………(4分)
(2)解:如图,取格点D,E,
在Rt△AEC中,tan∠ACE=;…………(1分)
在Rt△ABD中,tan∠ABD=;…………(2分)
∴tan∠ACE=tan∠ABD
∴∠ACE=∠ABD…………(3分)
直线BD与AC的交点为所求的点P.…………(4分)
19.(1)解:图中表示“内容”的扇形的圆心角度数为:108°. …(2分)
(2)解:m=7.6…(2分)
根据总评成绩三人的排名由高到低的顺序为:小亮,小田,小明.
…………………………………………(3分)
(3)学校要求“内容”比“表达”重要,则该统计图中各部分所占比例不合理.应作如下调整:内容占40%,表达占30. …(3分)
20.(1)解:k=4; ………………(4分)
(2)解:F的坐标为(2+,2-4).………………(4分)
21.解:点B表示的读数3.2cm.………………(8分)
22.(1)解:利润z(万元)与销售价格x函数解析式为:
z=-x2+12x-320…………(3分)
当x=60时,z最大,最大净利润为z=-×602+12×60-320=40(万元).
…………………………………………(5分)
(2)解:当z=17.5时,解方程17.5=-x2+12x-320得,x1=45,x2=75.……………………………………(2分)
∵净利润预期不低于17.5万元
∴由二次函数的图象性质可知,销售价格x(元/个)的取值范围为,45≤x≤75………………………(3分)
∵销售量y(万个)与x(元/个)之间的关系式为y=-x+9,由一次函数性质可知,y随x的增大而减小. …………(4分)
∴x=45时,销售量最大,故销售价应定为45元/个. …………(5分)
23.(1)证明:略 …………(3分)
(2)解:四边形ACBM是菱形.
如图,连接O1C,O1M,O2C,O2M,CM. …………(1分)
已知等圆⊙O1与⊙O2相交于C,M两点,
∴O1C=O1M=O2C=O2M, 即四边形CO2MO1为菱形,…………(2分)
∴CM与O1O2互相垂直平分,又,O2B=O1A,
∴AB,CM互相平分,且垂直,
∴四边形ACBM是菱形 …………(3分)
(3)解:BH·AE=8
连接O2D,O2F,
已知等圆⊙O1与⊙O2相交于C,M两点,DF=AB=2,
∴O2D=O2F=DF=AB=2,
∴△O2DF为等边三角形,
∴∠DO1E=∠DO2F=30°,
同理,△CO2O1为等边三角形,
∠A=∠B=30°① ……………………(1分)
∴∠EO1A+∠DO1B=∠BHO1+∠DO1B=150°
∴∠EO1A=∠BHO1② …………(2分)
由①②可得,△BHO1∽△AO1E
∴=,又,BO1=4,AO1=2;
∴BH·AE=8 …………………(3分)
(4)解:构造如图所示的辅助线,同(3)证∠DBF=30°.
∵D,B,F,O1四点在⊙O2上,
∴∠DO1E+∠DO1F=∠DBF+∠DO1F=180°.
∠DO1E=∠DBF=30°.…………(1分)
以下证明方法同(3),BH·AE=8 …………(3分)
24.(1)解:抛物线的解析式为:
y=x2-4x-5 ………(3分)
(2)解:如图,
直线AB的解析式为:y=x-5,且△ABO为等腰直角三角形,
直线AB与抛物线对称轴的交点E的坐标为(2,-3),ER=6,
作RF⊥AB,则△EFR为等腰直角三角形,RF=3=DG
当GH与抛物线只有一个交点时,
∵GH⊥AB,
∴可设GH的解析式为:y=-x+m
则关于x的一元二次方程-x+m=x2-4x-5有两相等实数根,
△=0,即,(-3)2-4(-5-m)=0,解得,m=-………(1分)
直线y=-x-与y=x-5的交点G的横坐标为-,
∵DH∥x轴,
∴∠GDH=∠OBA=45°,又GH⊥AB,
∴△DGH为等腰直角三角形,且DG=3
∴m=--3=-………(2分)
由平移的性质可知,
点H在过点R且平行于AB的直线RT上,RF=3=DG
∴点H与点R,T重合时,GH与抛物线有两个交点,
综上,m的取值范围是:
-<m≤-4,或m=-3………(3分)
(3)解:如图所示,连接BR, OO '=MN=2,O 'P⊥BR,垂足为P, P、Q关于抛物线y=x2-4x-5的对称轴对称,在此种情况下,由垂线段最短可知OM+NM+NQ的值最小. …………(2分)
O'P的解析式为:y=-x-2;
BR的解析式为:y=3x-15;
∴点P的坐标为(,-)
由抛物线的轴对称性可得,点Q与点P关于直线x=2对称,
∴点Q的坐标为(,-)…………(4分)
(第5题图)
(第8题图)
(第9题图)
(第20题图)
(第21题图)
(第23题图1)
(第23题图2)
(第23题图3)
PAGE
九年级数学试题卷
范围:九年级数学人教版上下册 考时:120分钟 满分:120分
注意事项:
1.本试卷分试题卷和答题卷两个部分。
2.答题前,请你务必将自己的姓名、准考证号填写在试题卷上,并填写答题卷上的考生信息。
3.选择题务必使用2B铅笔在答题卷选择题的答题区域内填涂;非选择题务必使用黑色签字笔在答题卷非选择题各题指定的答题区域内作答。填涂、书写在试题卷上的一律无效。
4.考试结束,试题卷、答题卷一并上交。
一、选择题(每小题3分,共36分)
1.如图所示的几何体是由 6 个完全相同的小立方块搭成,则这个几何体的左视图是(▲)
A. B. C. D.
2.已知x=2是一元二次方程x2+bx-b=0的解,则b=(▲)
A. -2 B.-4 C.0 D.4
3.抛物线y=-x2+3x-的对称轴是(▲)
A.x=6 B.x=-3 C.x=- D.x=3
4.下面图形中既是轴对称图形又是中心对称图形的是(▲)
A. B. C. D.
科克曲线 笛卡尔心形线 阿基米德螺旋线 赵爽弦图
5.扇子最早称“翣”,在我国已有两千多年历史.“打开半个月亮,收起兜里可装,来时荷花初放,去时菊花正黄.”这则谜语说的就是扇子. 如图,一竹扇完全打开后,外侧两竹条AB,AC夹角为135°,AB的长为30cm, 扇面BD
的长为20cm,则扇面面积为(▲)cm2
A.π B.600π C.300π D.30π
6.动物学家通过大量的调查估计,某种动物活到20岁的概率为0.8,活到25岁的概率为0.5,那么,现年20岁的这种动物活到25岁的概率是(▲)
A.0 B.1 C. D.
7.如图,已知A,B是反比例函数y=(k>0,x>0)图象上的两点,BC∥x轴,交y轴于点C,动点P从坐标原点O出发,沿O→A→B→C(图中“→”所示路线)匀速运动,终点为C,过P作PM⊥x轴,垂足为M.设三角形OMP的面积为S,P点运动时间为t,则S关于t的函数图象大致为(▲)
A. B. C. D.
8.如图,△ABC中,=,则下列结论不正确的是(▲)
A.△ADE∽△ABC B.=
C.= D.DE∥BC
9.在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,=,则tan∠B=(▲)
A. B. C. D.
10.已知a,b是关于x的一元二次方程x2+3x-1=0的两个实数根,则(a+2)2+b的值为(▲)
A. B.5 C.2 D.-2
11.在平面直角坐标系xoy中,已知A(1,0), C(-2,1), 若将点C绕点A顺时针旋转90°得到点C',则C'的坐标为(▲)
A.(2,3) B.(1,2) C.(2,1) D.(3,2)
12.抛物线y=ax2+bx+c(a>0)与x轴交于点A(-2,0),对称轴为x=-. 下列结论正确:
①a+b+c>0 ②2b+c=0 ③2c-a≥m(am+b)+c 其中正确的有(▲)个.
A.1 B.2 C.3 D.0
二、填空题(每小题3分,共计12分)
13.一个用电器的电阻是可调节的,其范围为110∽220Ω.已知电压为220V,这个用电器的电路图如图所示,则这个用电器功率的范围是▲.
(第13题图) (第14题图)
14.如图,某零件的外径为10cm,用一个交叉卡钳(两条尺长AC和BD相等)可测量零件的内孔直径AB.如果OA:OC=OB:OD=3,且量得CD=3cm,则零件的厚度x为▲cm.
15.往直径为26cm的圆柱形油槽内注入一些油以后,若油面宽度12cm,则油面的深度为▲.
16.在平面直角坐标系xoy中,将抛物线y=x2-2x+3先绕原点O旋转180°,再向上平移3个单位,则平移后的抛物线解析式为▲.
三、解答题(共72分)
17.(8分)化简求值:(+)÷,其中,a为的小数部分.
18.(8分)(1)在如图1的正方形网格图中,每个小正方形的边长为1,A,B,C,D均为格点(小正方形的顶点). 求证:∠ABC=∠D.
(2)在如图2所示的正方形网格图中,每个小正方形的边长为1,A,B,C均为格点,请你仅用无刻度的直尺在线段AC上求作一点P, 使得∠PBA=∠C,并简要说明理由.
(第18题图1) (第18题图2)
19.(8分)学校举办演讲比赛,总评成绩由“内容、表达、风度、印象”四部分组成.九(1)班组织选拔赛,制定的各部分所占比例及三位同学的成绩如下统计图表所示.
演讲总评成绩各部分所占比例的统计图 三位同学的成绩统计表
请根据以上信息解答下列问题:
(1)求图中表示“内容”的扇形的圆心角度数.
(2)求表中m的值,并根据总评成绩确定三人的排名顺序.
(3)学校要求“内容”比“表达”重要,该统计图中各部分所占比例是否合理?如果不合理,如何调整?
20.(8分)在平面直角坐标系xoy中,已知A(4,0),B(0,2),四边形ABCD为正方形,双曲线y= (k≠0)经过边BC的中点E.
(1)求k的值;
(2)求(1)中双曲线与边AD的交点F的坐标.
21.(8分)如图,将含45°的直角三角板按下面的方式放置在一把刻度尺上,三角板与刻度尺下沿的边重合,三角板的一个顶点A在刻度尺的读数0cm刻度线的正下方,按上述方法将一个37°的∠MAG放置在该刻度尺上,若点H表示的读数为2.4cm,求点B表示的读数(精确到0.1cm), 参考数据sin37°≈0.602, con37°≈0.799, tan37°≈0.753)
22.(10分,荆门中考)商场销售一种进价为30元/个的商品,当销售价格为x(元/个)满足40<x<80时,其销售量y(万个)与x之间的关系式为y=-x+9,同时销售过程中的其它开支为50万元.
(1)求出商场销售这种商品的净利润z(万元)与销售价格x函数解析式,销售价格x定为多少时,净利润最大,最大净利润是多少?
(2)若净利润预期不低于17.5万元,试求出销售价格x(元/个)的取值范围;若还需要考虑销售量尽可能大,销售价格x应定为多少元?
23.(12分)如图1,等圆⊙O1与⊙O2相交于C,M两点,⊙O1经过⊙O2的圆心O2,直线O1O2交⊙O1于点A,交⊙O2于点B,连接AC,BC.
(1)求证:BC为⊙O1的切线;AC为⊙O2的切线;
(2)连接BM, AM, 判断四边形ACBM的形状,并说明理由;
(3)如图2,当点H为线段BC上的点,点E为AC延长线上的点,直线O1H交O2于点D,直线O1E交O2于点F.若DF=AB=2,探求BH·AE是否为定值;
(4)如图3,当H为BC延长线上的点,E为线段AC上的点,其它条件不变,则(3)中的结论是否仍然成立?请说明理由.
24.(10分)如图1,抛物线y=ax2+bx+c(a≠0)与y轴交于点A(0,-5),与x轴交于B,C两点(点B在点C的右侧),其顶点R(2,-9).
(1)求抛物线解析式(直接写出结果);
(2)如图1,点D,G在直线AB上,DG=3, GH⊥AB,DH∥x轴,设D(m,n),若线段GH与抛物线有两个交点时,求m的取值范围;
(3)如图2,点Q是线段CR上的动点,N,M为抛物线对称轴上的点,点M在点N的上方,且MN=2,连接OM,QN. 当OM+NM+NQ的值最小时,求点Q的坐标.
(第24题图1) (第24题图2)
参考答案
一、选择题
B B D A C D C C C C A A
二、填空题
13. 220~440 w (没有单位扣1分)
14.
15.13- cm或13+ cm (没有单位扣1分)
16.y=-x2-2x
三、解答题
17.解: 原式=-……………(5分)
a为的小数部分,则a=-2 …………(6分)
原式=- …………(8分)
18.(1)证明:略…………(4分)
(2)解:如图,取格点D,E,
在Rt△AEC中,tan∠ACE=;…………(1分)
在Rt△ABD中,tan∠ABD=;…………(2分)
∴tan∠ACE=tan∠ABD
∴∠ACE=∠ABD…………(3分)
直线BD与AC的交点为所求的点P.…………(4分)
19.(1)解:图中表示“内容”的扇形的圆心角度数为:108°. …(2分)
(2)解:m=7.6…(2分)
根据总评成绩三人的排名由高到低的顺序为:小亮,小田,小明.
…………………………………………(3分)
(3)学校要求“内容”比“表达”重要,则该统计图中各部分所占比例不合理.应作如下调整:内容占40%,表达占30. …(3分)
20.(1)解:k=4; ………………(4分)
(2)解:F的坐标为(2+,2-4).………………(4分)
21.解:点B表示的读数3.2cm.………………(8分)
22.(1)解:利润z(万元)与销售价格x函数解析式为:
z=-x2+12x-320…………(3分)
当x=60时,z最大,最大净利润为z=-×602+12×60-320=40(万元).
…………………………………………(5分)
(2)解:当z=17.5时,解方程17.5=-x2+12x-320得,x1=45,x2=75.……………………………………(2分)
∵净利润预期不低于17.5万元
∴由二次函数的图象性质可知,销售价格x(元/个)的取值范围为,45≤x≤75………………………(3分)
∵销售量y(万个)与x(元/个)之间的关系式为y=-x+9,由一次函数性质可知,y随x的增大而减小. …………(4分)
∴x=45时,销售量最大,故销售价应定为45元/个. …………(5分)
23.(1)证明:略 …………(3分)
(2)解:四边形ACBM是菱形.
如图,连接O1C,O1M,O2C,O2M,CM. …………(1分)
已知等圆⊙O1与⊙O2相交于C,M两点,
∴O1C=O1M=O2C=O2M, 即四边形CO2MO1为菱形,…………(2分)
∴CM与O1O2互相垂直平分,又,O2B=O1A,
∴AB,CM互相平分,且垂直,
∴四边形ACBM是菱形 …………(3分)
(3)解:BH·AE=8
连接O2D,O2F,
已知等圆⊙O1与⊙O2相交于C,M两点,DF=AB=2,
∴O2D=O2F=DF=AB=2,
∴△O2DF为等边三角形,
∴∠DO1E=∠DO2F=30°,
同理,△CO2O1为等边三角形,
∠A=∠B=30°① ……………………(1分)
∴∠EO1A+∠DO1B=∠BHO1+∠DO1B=150°
∴∠EO1A=∠BHO1② …………(2分)
由①②可得,△BHO1∽△AO1E
∴=,又,BO1=4,AO1=2;
∴BH·AE=8 …………………(3分)
(4)解:构造如图所示的辅助线,同(3)证∠DBF=30°.
∵D,B,F,O1四点在⊙O2上,
∴∠DO1E+∠DO1F=∠DBF+∠DO1F=180°.
∠DO1E=∠DBF=30°.…………(1分)
以下证明方法同(3),BH·AE=8 …………(3分)
24.(1)解:抛物线的解析式为:
y=x2-4x-5 ………(3分)
(2)解:如图,
直线AB的解析式为:y=x-5,且△ABO为等腰直角三角形,
直线AB与抛物线对称轴的交点E的坐标为(2,-3),ER=6,
作RF⊥AB,则△EFR为等腰直角三角形,RF=3=DG
当GH与抛物线只有一个交点时,
∵GH⊥AB,
∴可设GH的解析式为:y=-x+m
则关于x的一元二次方程-x+m=x2-4x-5有两相等实数根,
△=0,即,(-3)2-4(-5-m)=0,解得,m=-………(1分)
直线y=-x-与y=x-5的交点G的横坐标为-,
∵DH∥x轴,
∴∠GDH=∠OBA=45°,又GH⊥AB,
∴△DGH为等腰直角三角形,且DG=3
∴m=--3=-………(2分)
由平移的性质可知,
点H在过点R且平行于AB的直线RT上,RF=3=DG
∴点H与点R,T重合时,GH与抛物线有两个交点,
综上,m的取值范围是:
-<m≤-4,或m=-3………(3分)
(3)解:如图所示,连接BR, OO '=MN=2,O 'P⊥BR,垂足为P, P、Q关于抛物线y=x2-4x-5的对称轴对称,在此种情况下,由垂线段最短可知OM+NM+NQ的值最小. …………(2分)
O'P的解析式为:y=-x-2;
BR的解析式为:y=3x-15;
∴点P的坐标为(,-)
由抛物线的轴对称性可得,点Q与点P关于直线x=2对称,
∴点Q的坐标为(,-)…………(4分)
(第5题图)
(第8题图)
(第9题图)
(第20题图)
(第21题图)
(第23题图1)
(第23题图2)
(第23题图3)
PAGE
同课章节目录
