2014快乐暑假初三升初四衔接复习部分————矩形(附答案)
文档属性
| 名称 | 2014快乐暑假初三升初四衔接复习部分————矩形(附答案) | 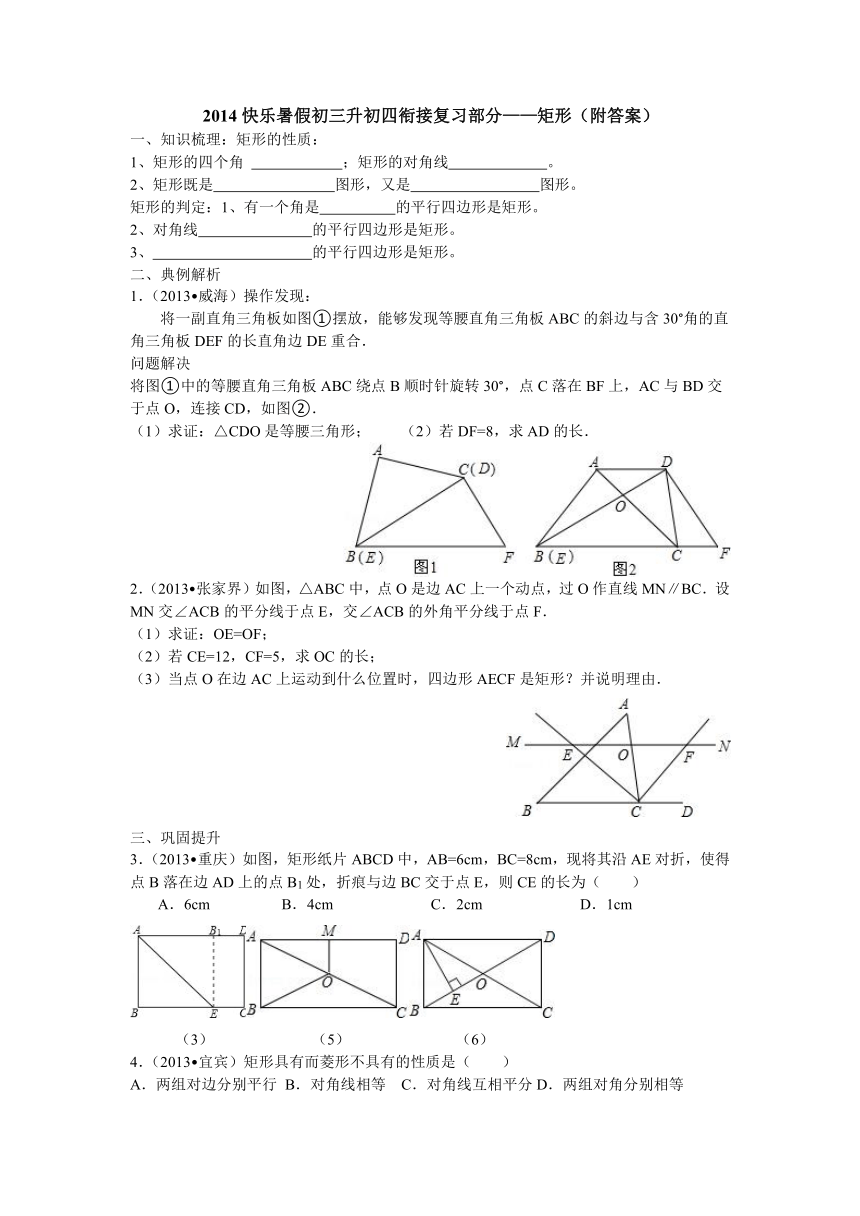 | |
| 格式 | zip | ||
| 文件大小 | 137.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-07-14 21:28:50 | ||
图片预览


文档简介
2014快乐暑假初三升初四衔接复习部分——矩形(附答案)
一、知识梳理:矩形的性质:
1、矩形的四个角 ;矩形的对角线 。
2、矩形既是 图形,又是 图形。
矩形的判定:1、有一个角是 的平行四边形是矩形。
2、对角线 的平行四边形是矩形。
3、 的平行四边形是矩形。
二、典例解析
1.(2013 威海)操作发现:
将一副直角三角板如图①摆放,能够发现等腰直角三角板ABC的斜边与含30°角的直角三角板DEF的长直角边DE重合.
问题解决
将图①中的等腰直角三角板ABC绕点B顺时针旋转30°,点C落在BF上,AC与BD交于点O,连接CD,如图②.
(1)求证:△CDO是等腰三角形; (2)若DF=8,求AD的长.
( http: / / www.21cnjy.com )
2.(2013 张家界)如图,△ABC中 ( http: / / www.21cnjy.com ),点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
(1)求证:OE=OF;
(2)若CE=12,CF=5,求OC的长;
(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.
( http: / / www.21cnjy.com )
三、巩固提升
3.(2013 重庆)如图,矩形纸片ABC ( http: / / www.21cnjy.com )D中,AB=6cm,BC=8cm,现将其沿AE对折,使得点B落在边AD上的点B1处,折痕与边BC交于点E,则CE的长为( )
A.6cm B. 4cm C. 2cm D. 1cm
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(3) (5) (6)
4.(2013 宜宾)矩形具有而菱形不具有的性质是( )
A.两组对边分别平行 B.对角线相等 C.对角线互相平分D.两组对角分别相等
5.(2013 北京)如图,O是矩形ABC ( http: / / www.21cnjy.com )D的对角线AC的中点,M是AD的中点.若AB=5,AD=12,则四边形ABOM的周长为 _________ .
6.(2010 北海)在矩形ABCD中,对角线AC、BD交于点O,AE⊥BD,且AE平分∠BAO.则∠AOB= 度.
7.(2014 遂宁)已知 ( http: / / www.21cnjy.com ):如图,在矩形ABCD中,对角线AC、BD相交于点O,E是CD中点,连结OE.过点C作CF∥BD交线段OE的延长线于点F,连结DF.求证:
(1)△ODE≌△FCE;
(2)四边形ODFC是菱形.
( http: / / www.21cnjy.com )
8.(2014 安顺)已知:如图,在△ ( http: / / www.21cnjy.com )ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E,
(1)求证:四边形ADCE为矩形;
(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明.
( http: / / www.21cnjy.com )
四、拔高训练
9.(2010 铜仁地区)如图,顺次连接四边形ABCD各边中点得四边形EFGH,要使四边形EFGH为矩形,应添加的条件是( )
A. AB∥DC B. AC=BD C. AC⊥BD D. AB=DC
( http: / / www.21cnjy.com )
10.(2011 兰州)如图,依次 ( http: / / www.21cnjy.com )连接第一个矩形各边的中点得到一个菱形,再依次连接菱形各边的中点得到第二个矩形,按照此方法继续下去.已知第一个矩形的面积为1,则第n个矩形的面积为 _________ .
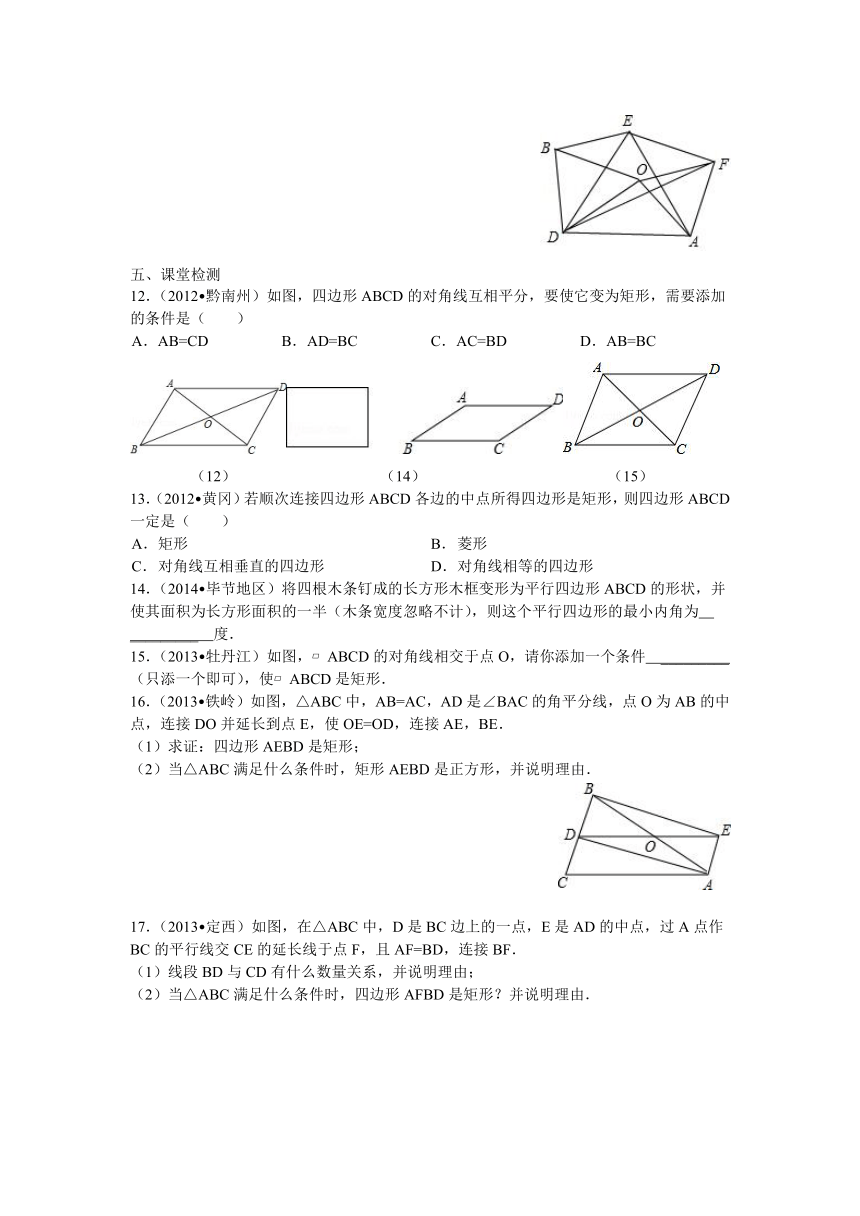
11.(2010 江干区模拟)如图 ( http: / / www.21cnjy.com ),以△AOD的三边为边,在AD的同侧作三个等边三角形△AED、△BOD、△AOF,请回答下列问题并说明理由:
(1)四边形OBEF是什么四边形?
(2)当△AOD满足什么条件时,四边形OBEF是菱形?是矩形?
(3)当△AOD满足什么条件时,以O、B、E、F为顶点的四边形不存在?
( http: / / www.21cnjy.com )
五、课堂检测
12.(2012 黔南州)如图,四边形ABCD的对角线互相平分,要使它变为矩形,需要添加的条件是( )
A. AB=CD B. AD=BC C. AC=BD D. AB=BC
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(12) (14) (15)
13.(2012 黄冈)若顺次连接四边形ABCD各边的中点所得四边形是矩形,则四边形ABCD一定是( )
A. 矩形 B. 菱形
C. 对角线互相垂直的四边形 D. 对角线相等的四边形
14.(2014 毕节地区)将四根木条钉成的 ( http: / / www.21cnjy.com )长方形木框变形为平行四边形ABCD的形状,并使其面积为长方形面积的一半(木条宽度忽略不计),则这个平行四边形的最小内角为 _________ 度.
15.(2013 牡丹江)如图, ABCD的对角线相交于点O,请你添加一个条件 _________ (只添一个即可),使 ABCD是矩形.
16.(2013 铁岭)如 ( http: / / www.21cnjy.com )图,△ABC中,AB=AC,AD是∠BAC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.
(1)求证:四边形AEBD是矩形;
(2)当△ABC满足什么条件时,矩形AEBD是正方形,并说明理由.
( http: / / www.21cnjy.com )
17.(2013 定西) ( http: / / www.21cnjy.com )如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.
(1)线段BD与CD有什么数量关系,并说明理由;
(2)当△ABC满足什么条件时,四边形AFBD是矩形?并说明理由.
( http: / / www.21cnjy.com )
18.(2013 大庆)已知△ABC是 ( http: / / www.21cnjy.com )等边三角形,点D、F分别在边BC、AC上,且DF∥AB,过点A平行于BC的直线与DF的延长线交于点E,连结CE、BF.
(1)求证:△ABF≌△ACE;
(2)若D是BC的中点,判断△DCE的形状,并说明理由.
( http: / / www.21cnjy.com )
19.(2012 青岛)已知:如图,四 ( http: / / www.21cnjy.com )边形ABCD的对角线AC、BD交于点O,BE⊥AC于E,DF⊥AC于F,点O既是AC的中点,又是EF的中点.
(1)求证:△BOE≌△DOF;
(2)若OA=BD,则四边形ABCD是什么特殊四边形?说明理由.
( http: / / www.21cnjy.com )
2014快乐暑假初三升初四衔接复习部分——矩形参考答案
1.分析:(1)根据题意可得BC= ( http: / / www.21cnjy.com )DE,进而得到∠BDC=∠BCD,再根据三角形内角和定理计算出度数,然后再根据三角形内角与外角的性质可得∠DOC=∠DBC+∠BCA,进而算出度数,根据角度可得△CDO是等腰三角形;
(2)作AG⊥BC,垂足为点G,DH⊥BF,垂足为点H,首先根据∠F=60°,DF=8,可以算出DH=4,HF=4,DB=8,BF=16,进而得到BC=8,再根据等腰三角形的性质可得BG=AG=4,证明四边形AGHD为矩形,根据线段的和差关系可得AD长.
(1)证明:由图①知BC=DE,
∴∠BDC=∠BCD,∵∠DEF=30°,∴∠BDC=∠BCD=75°,
∵∠ACB=45°,∵∠DCO+∠BCO=75°∴∠DCO=30°
∵∠DCO+∠CDO+∠DOC=180°,∴∠DOC=30°+45°=75°,
∴∠DOC=∠BDC,∴△CDO是等腰三角形;
(2)解:作AG⊥BC,垂足为点G,DH⊥BF,垂足为点H,
在Rt△DHF中,∠F=60°,DF=8,∴DH=4,HF=4,
在Rt△BDF中,∠F=60°,DF=8,∴DB=8,BF=16,∴BC=BD=8,
∵AG⊥BC,∠ABC=45°,∴BG=AG=4,∴AG=DH,
∵AG∥DH,AG⊥BC, ∴四边形AGHD为矩形,
∴AD=GH=BF﹣BG﹣HF=16﹣4﹣4=12﹣4.
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
2.(1)证明:∵MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F,
∴∠2=∠5,∠4=∠6,
∵MN∥BC,∴∠1=∠5,∠3=∠6,∴∠1=∠2,∠3=∠4,
∴EO=CO,FO=CO,∴OE=OF;
(2)解:∵∠2=∠5,∠4=∠6,∴∠2+∠4=∠5+∠6=90°,
∵CE=12,CF=5,∴EF==13,∴OC=EF=6.5;
(3)解:当点O在边AC上运动到AC中点时,四边形AECF是矩形.
证明:当O为AC的中点时,AO=CO,
∵EO=FO,∴四边形AECF是平行四边形,
∵∠ECF=90°,∴平行四边形AECF是矩形.
( http: / / www.21cnjy.com )
3.C.4.B.5. 20
6.解:∵AE⊥BD,∴∠AEB=∠AEO=90°,又∵AE平分∠BAO,∴∠BAE=∠OAE,
∵AE=AE,∴△AEB≌△AEO,∴AB=AO,
又∵四边形ABCD是矩形,∴AO=BO,∴AB=BO=AO,则△AOB是等边三角形,
∴∠AOB=60°.
7.证明:(1)∵CF∥BD,∴∠DOE=∠CFE,
∵E是CD中点,∴CE=DE,
在△ODE和△FCE中,,∴△ODE≌△FCE(ASA);
(2)∵△ODE≌△FCE,∴OD=FC,
∵CF∥BD,∴四边形ODFC是平行四边形,
在矩形ABCD中,OC=OD,∴四边形ODFC是菱形.
8.(1)证明:在△ABC中,AB=AC,AD⊥BC,∴∠BAD=∠DAC,
∵AN是△ABC外角∠CAM的平分线,∴∠MAE=∠CAE,
∴∠DAE=∠DAC+∠CAE=180°=90°,
又∵AD⊥BC,CE⊥AN,∴∠ADC=∠CEA=90°,∴四边形ADCE为矩形.
(2)当△ABC满足∠BAC=90°时,四边形ADCE是一个正方形.
理由:∵AB=AC,∴∠ACB=∠B=45°,
∵AD⊥BC,∴∠CAD=∠ACD=45°,∴DC=AD,
∵四边形ADCE为矩形,∴矩形ADCE是正方形.
∴当∠BAC=90°时,四边形ADCE是一个正方形.
9.C.10.()n﹣1
11。解:(1)平行四边形;
∵△AED和△OBD都是等边三角形,∴∠ADE=∠ODB=60°,AD=ED OD=BD,
∴∠ADE﹣∠ODE=∠ODB﹣∠ODE 即∠ADO=∠EDB,
∴△ADO≌△EDB.∴AO=EB,
∵△AOF是等边三角形,AO=FO,∴FO=EB
同理:BO=FE ∴四边形OBEF是平行四边形
(2)当OA=OD时,四边形OBEF为菱形,
当∠AOD=150°时,四边形OBEF为矩形;
(3)当∠AOD=60°时,以O、B、E、F为顶点的四边形不存在.
12.C.13.C.14. 30 15.AC=BD (只添一个即可)
16.(1)证明:∵点O为AB的中点,连接DO并延长到点E,使OE=OD,
∴四边形AEBD是平行四边形,
∵AB=AC,AD是∠BAC的角平分线,∴AD⊥BC,∴∠ADB=90°,
∴平行四边形AEBD是矩形;
(2)当∠BAC=90°时,
理由:∵∠BAC=90°,AB=AC,AD是∠BAC的角平分线,∴AD=BD=CD,
∵由(1)得四边形AEBD是矩形,∴矩形AEBD是正方形.
17.
解:(1)BD=CD.
理由如下:依题意得AF∥BC,∴∠AFE=∠DCE,
∵E是AD的中点,∴AE=DE,
在△AEF和△DEC中,,∴△AEF≌△DEC(AAS),∴AF=CD,
∵AF=BD,∴BD=CD;
(2)当△ABC满足:AB=AC时,四边形AFBD是矩形.
理由如下:∵AF∥BD,AF=BD,∴四边形AFBD是平行四边形,
∵AB=AC,BD=CD(三线合一),
∴∠ADB=90°,∴ AFBD是矩形.
18.(1)证明:∵△ABC是等边三角形,∴AB=AC,∠BAC=∠ACB=60°,
∵DE∥AB,AE∥BD,∴∠EFA=∠BAC=60°,∠CAE=∠ACB=60°,
∴△EAF是等边三角形,∴AF=AE,
在△ABF和△ACE中,∵,∴△ABF≌△ACE(SAS).
(2)△DCE是直角三角形,∠DCE=90°.
理由:连接AD,
∵DE∥AB,AE∥BD,∴四边形ABDE是平行四边形,∴AE=BD,
∵D是BC中点,∴BD=DC,∴AE=DC,
∵AE∥DC,∴四边形ADCE是平行四边形,
∵AB=AC,D是BC中点,
∴AD⊥DC,∴四边形ADCE是矩形,∴△DCE是直角三角形,∠DCE=90°.
19、(1)证明:∵BE⊥AC.DF⊥AC,∴∠BEO=∠DFO=90°,
∵点O是EF的中点,∴OE=OF,
又∵∠DOF=∠BOE,∴△BOE≌△DOF(ASA);
(2)解:四边形ABCD是矩形.理由如下:
∵△BOE≌△DOF,∴OB=OD,
又∵OA=OC,∴四边形ABCD是平行四边形,
∵OA=BD,OA=AC,
∴BD=AC,
∴ ABCD是矩形.
一、知识梳理:矩形的性质:
1、矩形的四个角 ;矩形的对角线 。
2、矩形既是 图形,又是 图形。
矩形的判定:1、有一个角是 的平行四边形是矩形。
2、对角线 的平行四边形是矩形。
3、 的平行四边形是矩形。
二、典例解析
1.(2013 威海)操作发现:
将一副直角三角板如图①摆放,能够发现等腰直角三角板ABC的斜边与含30°角的直角三角板DEF的长直角边DE重合.
问题解决
将图①中的等腰直角三角板ABC绕点B顺时针旋转30°,点C落在BF上,AC与BD交于点O,连接CD,如图②.
(1)求证:△CDO是等腰三角形; (2)若DF=8,求AD的长.
( http: / / www.21cnjy.com )
2.(2013 张家界)如图,△ABC中 ( http: / / www.21cnjy.com ),点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
(1)求证:OE=OF;
(2)若CE=12,CF=5,求OC的长;
(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.
( http: / / www.21cnjy.com )
三、巩固提升
3.(2013 重庆)如图,矩形纸片ABC ( http: / / www.21cnjy.com )D中,AB=6cm,BC=8cm,现将其沿AE对折,使得点B落在边AD上的点B1处,折痕与边BC交于点E,则CE的长为( )
A.6cm B. 4cm C. 2cm D. 1cm
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(3) (5) (6)
4.(2013 宜宾)矩形具有而菱形不具有的性质是( )
A.两组对边分别平行 B.对角线相等 C.对角线互相平分D.两组对角分别相等
5.(2013 北京)如图,O是矩形ABC ( http: / / www.21cnjy.com )D的对角线AC的中点,M是AD的中点.若AB=5,AD=12,则四边形ABOM的周长为 _________ .
6.(2010 北海)在矩形ABCD中,对角线AC、BD交于点O,AE⊥BD,且AE平分∠BAO.则∠AOB= 度.
7.(2014 遂宁)已知 ( http: / / www.21cnjy.com ):如图,在矩形ABCD中,对角线AC、BD相交于点O,E是CD中点,连结OE.过点C作CF∥BD交线段OE的延长线于点F,连结DF.求证:
(1)△ODE≌△FCE;
(2)四边形ODFC是菱形.
( http: / / www.21cnjy.com )
8.(2014 安顺)已知:如图,在△ ( http: / / www.21cnjy.com )ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E,
(1)求证:四边形ADCE为矩形;
(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明.
( http: / / www.21cnjy.com )
四、拔高训练
9.(2010 铜仁地区)如图,顺次连接四边形ABCD各边中点得四边形EFGH,要使四边形EFGH为矩形,应添加的条件是( )
A. AB∥DC B. AC=BD C. AC⊥BD D. AB=DC
( http: / / www.21cnjy.com )
10.(2011 兰州)如图,依次 ( http: / / www.21cnjy.com )连接第一个矩形各边的中点得到一个菱形,再依次连接菱形各边的中点得到第二个矩形,按照此方法继续下去.已知第一个矩形的面积为1,则第n个矩形的面积为 _________ .
11.(2010 江干区模拟)如图 ( http: / / www.21cnjy.com ),以△AOD的三边为边,在AD的同侧作三个等边三角形△AED、△BOD、△AOF,请回答下列问题并说明理由:
(1)四边形OBEF是什么四边形?
(2)当△AOD满足什么条件时,四边形OBEF是菱形?是矩形?
(3)当△AOD满足什么条件时,以O、B、E、F为顶点的四边形不存在?
( http: / / www.21cnjy.com )
五、课堂检测
12.(2012 黔南州)如图,四边形ABCD的对角线互相平分,要使它变为矩形,需要添加的条件是( )
A. AB=CD B. AD=BC C. AC=BD D. AB=BC
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(12) (14) (15)
13.(2012 黄冈)若顺次连接四边形ABCD各边的中点所得四边形是矩形,则四边形ABCD一定是( )
A. 矩形 B. 菱形
C. 对角线互相垂直的四边形 D. 对角线相等的四边形
14.(2014 毕节地区)将四根木条钉成的 ( http: / / www.21cnjy.com )长方形木框变形为平行四边形ABCD的形状,并使其面积为长方形面积的一半(木条宽度忽略不计),则这个平行四边形的最小内角为 _________ 度.
15.(2013 牡丹江)如图, ABCD的对角线相交于点O,请你添加一个条件 _________ (只添一个即可),使 ABCD是矩形.
16.(2013 铁岭)如 ( http: / / www.21cnjy.com )图,△ABC中,AB=AC,AD是∠BAC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.
(1)求证:四边形AEBD是矩形;
(2)当△ABC满足什么条件时,矩形AEBD是正方形,并说明理由.
( http: / / www.21cnjy.com )
17.(2013 定西) ( http: / / www.21cnjy.com )如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.
(1)线段BD与CD有什么数量关系,并说明理由;
(2)当△ABC满足什么条件时,四边形AFBD是矩形?并说明理由.
( http: / / www.21cnjy.com )
18.(2013 大庆)已知△ABC是 ( http: / / www.21cnjy.com )等边三角形,点D、F分别在边BC、AC上,且DF∥AB,过点A平行于BC的直线与DF的延长线交于点E,连结CE、BF.
(1)求证:△ABF≌△ACE;
(2)若D是BC的中点,判断△DCE的形状,并说明理由.
( http: / / www.21cnjy.com )
19.(2012 青岛)已知:如图,四 ( http: / / www.21cnjy.com )边形ABCD的对角线AC、BD交于点O,BE⊥AC于E,DF⊥AC于F,点O既是AC的中点,又是EF的中点.
(1)求证:△BOE≌△DOF;
(2)若OA=BD,则四边形ABCD是什么特殊四边形?说明理由.
( http: / / www.21cnjy.com )
2014快乐暑假初三升初四衔接复习部分——矩形参考答案
1.分析:(1)根据题意可得BC= ( http: / / www.21cnjy.com )DE,进而得到∠BDC=∠BCD,再根据三角形内角和定理计算出度数,然后再根据三角形内角与外角的性质可得∠DOC=∠DBC+∠BCA,进而算出度数,根据角度可得△CDO是等腰三角形;
(2)作AG⊥BC,垂足为点G,DH⊥BF,垂足为点H,首先根据∠F=60°,DF=8,可以算出DH=4,HF=4,DB=8,BF=16,进而得到BC=8,再根据等腰三角形的性质可得BG=AG=4,证明四边形AGHD为矩形,根据线段的和差关系可得AD长.
(1)证明:由图①知BC=DE,
∴∠BDC=∠BCD,∵∠DEF=30°,∴∠BDC=∠BCD=75°,
∵∠ACB=45°,∵∠DCO+∠BCO=75°∴∠DCO=30°
∵∠DCO+∠CDO+∠DOC=180°,∴∠DOC=30°+45°=75°,
∴∠DOC=∠BDC,∴△CDO是等腰三角形;
(2)解:作AG⊥BC,垂足为点G,DH⊥BF,垂足为点H,
在Rt△DHF中,∠F=60°,DF=8,∴DH=4,HF=4,
在Rt△BDF中,∠F=60°,DF=8,∴DB=8,BF=16,∴BC=BD=8,
∵AG⊥BC,∠ABC=45°,∴BG=AG=4,∴AG=DH,
∵AG∥DH,AG⊥BC, ∴四边形AGHD为矩形,
∴AD=GH=BF﹣BG﹣HF=16﹣4﹣4=12﹣4.
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
2.(1)证明:∵MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F,
∴∠2=∠5,∠4=∠6,
∵MN∥BC,∴∠1=∠5,∠3=∠6,∴∠1=∠2,∠3=∠4,
∴EO=CO,FO=CO,∴OE=OF;
(2)解:∵∠2=∠5,∠4=∠6,∴∠2+∠4=∠5+∠6=90°,
∵CE=12,CF=5,∴EF==13,∴OC=EF=6.5;
(3)解:当点O在边AC上运动到AC中点时,四边形AECF是矩形.
证明:当O为AC的中点时,AO=CO,
∵EO=FO,∴四边形AECF是平行四边形,
∵∠ECF=90°,∴平行四边形AECF是矩形.
( http: / / www.21cnjy.com )
3.C.4.B.5. 20
6.解:∵AE⊥BD,∴∠AEB=∠AEO=90°,又∵AE平分∠BAO,∴∠BAE=∠OAE,
∵AE=AE,∴△AEB≌△AEO,∴AB=AO,
又∵四边形ABCD是矩形,∴AO=BO,∴AB=BO=AO,则△AOB是等边三角形,
∴∠AOB=60°.
7.证明:(1)∵CF∥BD,∴∠DOE=∠CFE,
∵E是CD中点,∴CE=DE,
在△ODE和△FCE中,,∴△ODE≌△FCE(ASA);
(2)∵△ODE≌△FCE,∴OD=FC,
∵CF∥BD,∴四边形ODFC是平行四边形,
在矩形ABCD中,OC=OD,∴四边形ODFC是菱形.
8.(1)证明:在△ABC中,AB=AC,AD⊥BC,∴∠BAD=∠DAC,
∵AN是△ABC外角∠CAM的平分线,∴∠MAE=∠CAE,
∴∠DAE=∠DAC+∠CAE=180°=90°,
又∵AD⊥BC,CE⊥AN,∴∠ADC=∠CEA=90°,∴四边形ADCE为矩形.
(2)当△ABC满足∠BAC=90°时,四边形ADCE是一个正方形.
理由:∵AB=AC,∴∠ACB=∠B=45°,
∵AD⊥BC,∴∠CAD=∠ACD=45°,∴DC=AD,
∵四边形ADCE为矩形,∴矩形ADCE是正方形.
∴当∠BAC=90°时,四边形ADCE是一个正方形.
9.C.10.()n﹣1
11。解:(1)平行四边形;
∵△AED和△OBD都是等边三角形,∴∠ADE=∠ODB=60°,AD=ED OD=BD,
∴∠ADE﹣∠ODE=∠ODB﹣∠ODE 即∠ADO=∠EDB,
∴△ADO≌△EDB.∴AO=EB,
∵△AOF是等边三角形,AO=FO,∴FO=EB
同理:BO=FE ∴四边形OBEF是平行四边形
(2)当OA=OD时,四边形OBEF为菱形,
当∠AOD=150°时,四边形OBEF为矩形;
(3)当∠AOD=60°时,以O、B、E、F为顶点的四边形不存在.
12.C.13.C.14. 30 15.AC=BD (只添一个即可)
16.(1)证明:∵点O为AB的中点,连接DO并延长到点E,使OE=OD,
∴四边形AEBD是平行四边形,
∵AB=AC,AD是∠BAC的角平分线,∴AD⊥BC,∴∠ADB=90°,
∴平行四边形AEBD是矩形;
(2)当∠BAC=90°时,
理由:∵∠BAC=90°,AB=AC,AD是∠BAC的角平分线,∴AD=BD=CD,
∵由(1)得四边形AEBD是矩形,∴矩形AEBD是正方形.
17.
解:(1)BD=CD.
理由如下:依题意得AF∥BC,∴∠AFE=∠DCE,
∵E是AD的中点,∴AE=DE,
在△AEF和△DEC中,,∴△AEF≌△DEC(AAS),∴AF=CD,
∵AF=BD,∴BD=CD;
(2)当△ABC满足:AB=AC时,四边形AFBD是矩形.
理由如下:∵AF∥BD,AF=BD,∴四边形AFBD是平行四边形,
∵AB=AC,BD=CD(三线合一),
∴∠ADB=90°,∴ AFBD是矩形.
18.(1)证明:∵△ABC是等边三角形,∴AB=AC,∠BAC=∠ACB=60°,
∵DE∥AB,AE∥BD,∴∠EFA=∠BAC=60°,∠CAE=∠ACB=60°,
∴△EAF是等边三角形,∴AF=AE,
在△ABF和△ACE中,∵,∴△ABF≌△ACE(SAS).
(2)△DCE是直角三角形,∠DCE=90°.
理由:连接AD,
∵DE∥AB,AE∥BD,∴四边形ABDE是平行四边形,∴AE=BD,
∵D是BC中点,∴BD=DC,∴AE=DC,
∵AE∥DC,∴四边形ADCE是平行四边形,
∵AB=AC,D是BC中点,
∴AD⊥DC,∴四边形ADCE是矩形,∴△DCE是直角三角形,∠DCE=90°.
19、(1)证明:∵BE⊥AC.DF⊥AC,∴∠BEO=∠DFO=90°,
∵点O是EF的中点,∴OE=OF,
又∵∠DOF=∠BOE,∴△BOE≌△DOF(ASA);
(2)解:四边形ABCD是矩形.理由如下:
∵△BOE≌△DOF,∴OB=OD,
又∵OA=OC,∴四边形ABCD是平行四边形,
∵OA=BD,OA=AC,
∴BD=AC,
∴ ABCD是矩形.
