苏科版七年级数学下册第7章平面图形的认识(二)测试题(含答案)
文档属性
| 名称 | 苏科版七年级数学下册第7章平面图形的认识(二)测试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 186.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-10 21:23:38 | ||
图片预览

文档简介
(
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
苏科版七年级数学下册第7章测试题(附答案)
一、单选题
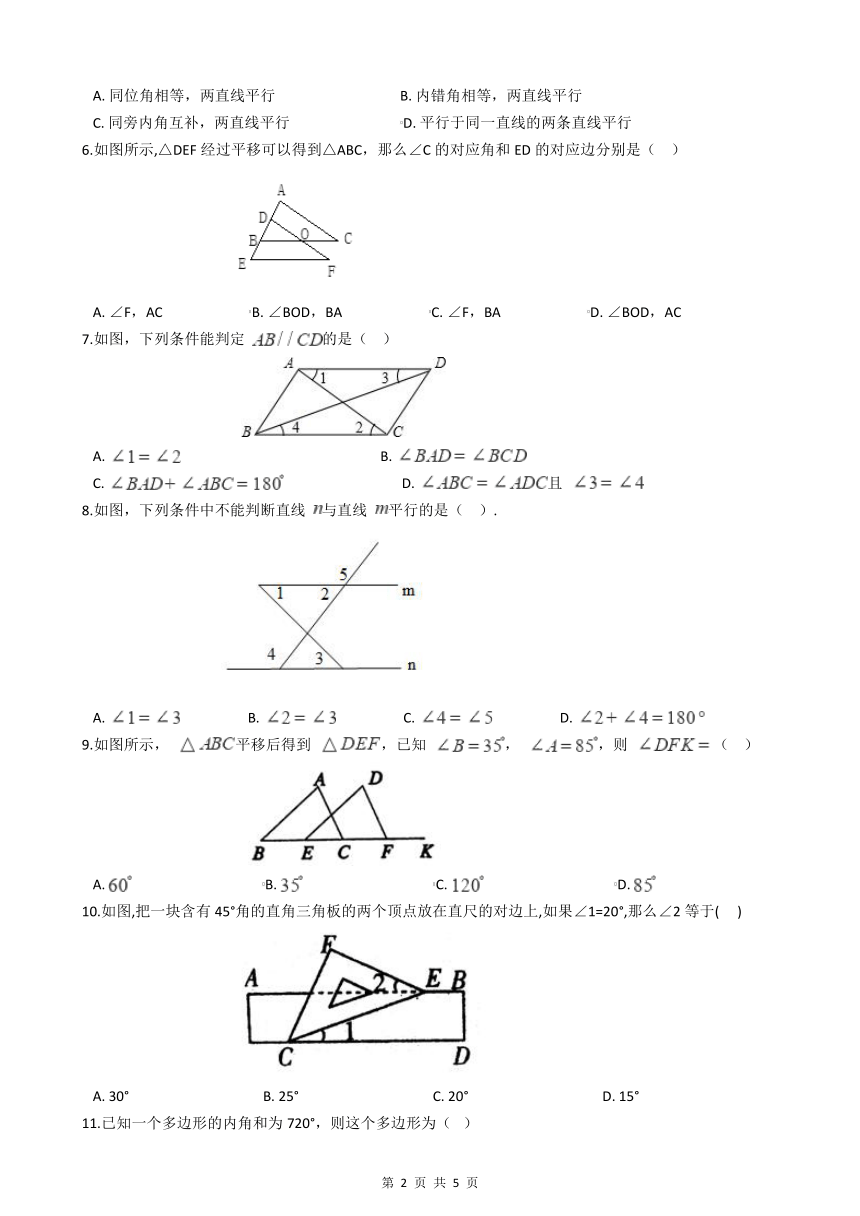
1.如图,若 , , ,则 的大小是( )
A. B. C. D.
2.具备下列条件的四个三角形中,不是直角三角形的是( )
A. ∠A ∠B ∠C B. ∠A-∠B 90° C. ∠A+∠B ∠C D. ∠A 90°-∠B
3.如图,将周长为18的△ABC沿BC方向平移2个单位得△DEF,则四边形ABFD的周长为( )
A. 22 B. 24 C. 26 D. 28
4.如图,已知 ,则 的度数是( )
A. B. C. D.
5.下图给出了过直线外一点作已知直线的平行线的一种方法,其依据是( )
A. 同位角相等,两直线平行 B. 内错角相等,两直线平行
C. 同旁内角互补,两直线平行 D. 平行于同一直线的两条直线平行
6.如图所示,△DEF经过平移可以得到△ABC,那么∠C的对应角和ED的对应边分别是( )
A. ∠F,AC B. ∠BOD,BA C. ∠F,BA D. ∠BOD,AC
7.如图,下列条件能判定 的是( )
A. B.
C. D. 且
8.如图,下列条件中不能判断直线 与直线 平行的是( ).
A. B. C. D.
9.如图所示, 平移后得到 ,已知 , ,则 ( )
A. B. C. D.
10.如图,把一块含有45°角的直角三角板的两个顶点放在直尺的对边上,如果∠1=20°,那么∠2等于( )
A. 30° B. 25° C. 20° D. 15°
11.已知一个多边形的内角和为720°,则这个多边形为( )
A. 三角形 B. 四边形 C. 五边形 D. 六边形
12.如图,能判定EB∥AC的条件是( )
A. ∠1=∠2 B. ∠3=∠4 C. ∠5=∠6 D. ∠2=∠3
二、填空题
13.一个多边形的每一个外角都等于18°,则这个多边形的边数是________.
14.已知三角形的三边长均为整数,其中两边长分别为1和3,则第三边长为________.
15.如图,在△ABC中,∠A=60°,若剪去∠A得到四边形BCDE,则∠1+∠2=________°.
16.如图,在△ABC中,E是BC上的一点,EC=2BE,点D是AC的中点,设△ABC、△ADF、△BEF的面积分别S、S1、S2 , 且S=36,则S1-S2=________.
17.小张同学观察如图1所示的北斗七星图,小张同学把北斗七星:摇光、开阳、玉衡、天权、天玑、天璇、天枢按图2分别标为点A、B、C、D、E、F、G,然后将点A、B、C、D、E、F、G顺次首尾连接,发现AG恰好经过点C,且∠B-∠DCG=115°,∠B-∠D=10°,若AG//EF,则∠E=m°,这里的m=________.
18.如图是用三角尺和直尺画平行线的示意图,将三角尺 沿着直尺 平移到三角尺 的位置,就可以画出 的平行线 .若 , ,则直线 平移的距离为________cm.
19.如图,将三角形ABC沿水平方向向右平移到三角形DEF的位置,若BF=11,EC=5,则A,D之间的距离为________.
20.如图,在 ABC 中,AD、CE 是中线,若四边形 BDFE 的面积是 6,则 ABC 的面积为________.
三、解答题
21.已知:如图,直线AB∥CD,直线EF与直线AB、CD分别交于点M、N,MG平分∠AMF,NH平分∠END.求证:MG∥NH.
22.如图,在 ABC中,F、H是BC上的点,FG⊥AC,HD⊥AC,垂足分别为G、D,在AB上取一点E,使∠BED+∠B=180°.求证:∠CFG=∠HDE.
23.如图,AB∥CD,∠AFE=140°,∠C=30°,求∠CEF的度数.
24.如图,已知∠1=∠2,∠GFA=40°,∠HAQ=15°,∠ACB=70°,AQ平分∠FAC , 求证:BD∥GE∥AH .
答 案
一、单选题
1. D 2. B 3. A 4. B 5. A 6. C 7. D 8. B 9. C 10. B 11. D 12. D
二、填空题
13. 20 14. 3 15. 240 16. 6 17. 18. 5.5 19. 3 20. 18
三、解答题
21. 证明:∵AB CD,
∴∠AMF=∠END,
∵MG平分∠AMF,NH平分∠END,
∴∠GMN= ∠AMF,∠HNM= ∠END,
∴∠GMN=∠HNM,
∴GM NH.
22. 证明:∵HD⊥AC,FG⊥AC,
∴∠CDH=∠CGF=90°.∴ FG∥HD.∴∠CFG=∠CHD.
∵∠BED+∠B=180°,∴ BC∥ED.∴∠CHD=∠HDE.∴∠CFG=∠HDE.
23. 解:延长FE交CD于G点,
∵AB∥CD, ∴∠AFE+∠CGF=180°,
∵∠AFE=140°,∴∠CGF=40°,
∵∠CEF=∠C+∠CGE,∠C=30°,∠CGE=∠CGF=40°,
∴∠CEF=∠C +∠CGE =70°.
24. 证明:∵∠1=∠2,
∴AH∥GE,∴∠GFA=∠FAH.
∵∠GFA=40°,
∴∠FAH=40°,∴∠FAQ=∠FAH+∠HAQ,
∴∠FAQ=55°.
又∵AQ平分∠FAC,∴∠QAC=∠FAQ=55°,
∵∠HAC=∠QAC+∠HAQ,
∴∠HAC=55°+15°=70°=∠ACB,∴BD∥AH,∴BD∥GE∥AH.
(
第
- 1 -
页 共
7
页
)
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
苏科版七年级数学下册第7章测试题(附答案)
一、单选题
1.如图,若 , , ,则 的大小是( )
A. B. C. D.
2.具备下列条件的四个三角形中,不是直角三角形的是( )
A. ∠A ∠B ∠C B. ∠A-∠B 90° C. ∠A+∠B ∠C D. ∠A 90°-∠B
3.如图,将周长为18的△ABC沿BC方向平移2个单位得△DEF,则四边形ABFD的周长为( )
A. 22 B. 24 C. 26 D. 28
4.如图,已知 ,则 的度数是( )
A. B. C. D.
5.下图给出了过直线外一点作已知直线的平行线的一种方法,其依据是( )
A. 同位角相等,两直线平行 B. 内错角相等,两直线平行
C. 同旁内角互补,两直线平行 D. 平行于同一直线的两条直线平行
6.如图所示,△DEF经过平移可以得到△ABC,那么∠C的对应角和ED的对应边分别是( )
A. ∠F,AC B. ∠BOD,BA C. ∠F,BA D. ∠BOD,AC
7.如图,下列条件能判定 的是( )
A. B.
C. D. 且
8.如图,下列条件中不能判断直线 与直线 平行的是( ).
A. B. C. D.
9.如图所示, 平移后得到 ,已知 , ,则 ( )
A. B. C. D.
10.如图,把一块含有45°角的直角三角板的两个顶点放在直尺的对边上,如果∠1=20°,那么∠2等于( )
A. 30° B. 25° C. 20° D. 15°
11.已知一个多边形的内角和为720°,则这个多边形为( )
A. 三角形 B. 四边形 C. 五边形 D. 六边形
12.如图,能判定EB∥AC的条件是( )
A. ∠1=∠2 B. ∠3=∠4 C. ∠5=∠6 D. ∠2=∠3
二、填空题
13.一个多边形的每一个外角都等于18°,则这个多边形的边数是________.
14.已知三角形的三边长均为整数,其中两边长分别为1和3,则第三边长为________.
15.如图,在△ABC中,∠A=60°,若剪去∠A得到四边形BCDE,则∠1+∠2=________°.
16.如图,在△ABC中,E是BC上的一点,EC=2BE,点D是AC的中点,设△ABC、△ADF、△BEF的面积分别S、S1、S2 , 且S=36,则S1-S2=________.
17.小张同学观察如图1所示的北斗七星图,小张同学把北斗七星:摇光、开阳、玉衡、天权、天玑、天璇、天枢按图2分别标为点A、B、C、D、E、F、G,然后将点A、B、C、D、E、F、G顺次首尾连接,发现AG恰好经过点C,且∠B-∠DCG=115°,∠B-∠D=10°,若AG//EF,则∠E=m°,这里的m=________.
18.如图是用三角尺和直尺画平行线的示意图,将三角尺 沿着直尺 平移到三角尺 的位置,就可以画出 的平行线 .若 , ,则直线 平移的距离为________cm.
19.如图,将三角形ABC沿水平方向向右平移到三角形DEF的位置,若BF=11,EC=5,则A,D之间的距离为________.
20.如图,在 ABC 中,AD、CE 是中线,若四边形 BDFE 的面积是 6,则 ABC 的面积为________.
三、解答题
21.已知:如图,直线AB∥CD,直线EF与直线AB、CD分别交于点M、N,MG平分∠AMF,NH平分∠END.求证:MG∥NH.
22.如图,在 ABC中,F、H是BC上的点,FG⊥AC,HD⊥AC,垂足分别为G、D,在AB上取一点E,使∠BED+∠B=180°.求证:∠CFG=∠HDE.
23.如图,AB∥CD,∠AFE=140°,∠C=30°,求∠CEF的度数.
24.如图,已知∠1=∠2,∠GFA=40°,∠HAQ=15°,∠ACB=70°,AQ平分∠FAC , 求证:BD∥GE∥AH .
答 案
一、单选题
1. D 2. B 3. A 4. B 5. A 6. C 7. D 8. B 9. C 10. B 11. D 12. D
二、填空题
13. 20 14. 3 15. 240 16. 6 17. 18. 5.5 19. 3 20. 18
三、解答题
21. 证明:∵AB CD,
∴∠AMF=∠END,
∵MG平分∠AMF,NH平分∠END,
∴∠GMN= ∠AMF,∠HNM= ∠END,
∴∠GMN=∠HNM,
∴GM NH.
22. 证明:∵HD⊥AC,FG⊥AC,
∴∠CDH=∠CGF=90°.∴ FG∥HD.∴∠CFG=∠CHD.
∵∠BED+∠B=180°,∴ BC∥ED.∴∠CHD=∠HDE.∴∠CFG=∠HDE.
23. 解:延长FE交CD于G点,
∵AB∥CD, ∴∠AFE+∠CGF=180°,
∵∠AFE=140°,∴∠CGF=40°,
∵∠CEF=∠C+∠CGE,∠C=30°,∠CGE=∠CGF=40°,
∴∠CEF=∠C +∠CGE =70°.
24. 证明:∵∠1=∠2,
∴AH∥GE,∴∠GFA=∠FAH.
∵∠GFA=40°,
∴∠FAH=40°,∴∠FAQ=∠FAH+∠HAQ,
∴∠FAQ=55°.
又∵AQ平分∠FAC,∴∠QAC=∠FAQ=55°,
∵∠HAC=∠QAC+∠HAQ,
∴∠HAC=55°+15°=70°=∠ACB,∴BD∥AH,∴BD∥GE∥AH.
(
第
- 1 -
页 共
7
页
)
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
