第八单元 第1课时 平均数(教学课件)-四年级数学下册人教版(共35张PPT)
文档属性
| 名称 | 第八单元 第1课时 平均数(教学课件)-四年级数学下册人教版(共35张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-11 00:00:00 | ||
图片预览






文档简介
(共35张PPT)
第1课时 平均数
小学数学·四年级(下)·RJ
增强与同伴交流的意识及体验运用所学知识解决问题的乐趣,增强学好数学的信心。
在具体的问题情境中,感受求平均数是解决一些实际问题的需要,通过操作体会平均数的意义,能计算简单数据的平均数。
经历用平均数解决简单生活问题的过程,进一步积累分析和处理数据的方法,发展统计观念,初步感知“移多补少”的数学思想。
理解平均数的意义,掌握求平均数的方法。
理解平均数的意义。
把概念的关键属性和学生的认知结构相联系,使学生掌握概念,并能总结方法。
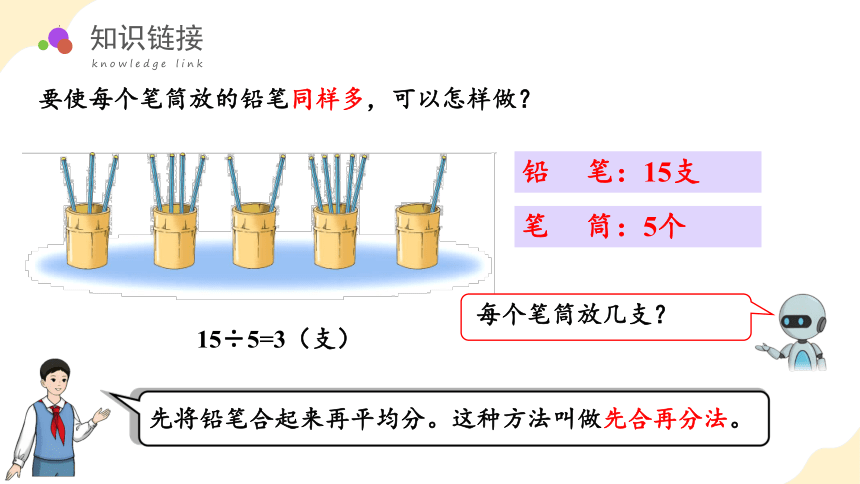
要使每个笔筒放的铅笔同样多,可以怎样做?
铅 笔:15支
笔 筒:5个
15÷5=3(支)
每个笔筒放几支?
先将铅笔合起来再平均分。这种方法叫做先合再分法。
拿出1支放入此笔筒
拿出2支放入此笔筒
要使每个笔筒放的铅笔同样多,可以怎样做?
还可以怎样分?
数量多的给数量少的一些,使它们的数量变得一样多,这种方法叫做移多补少法。。
认识平均数
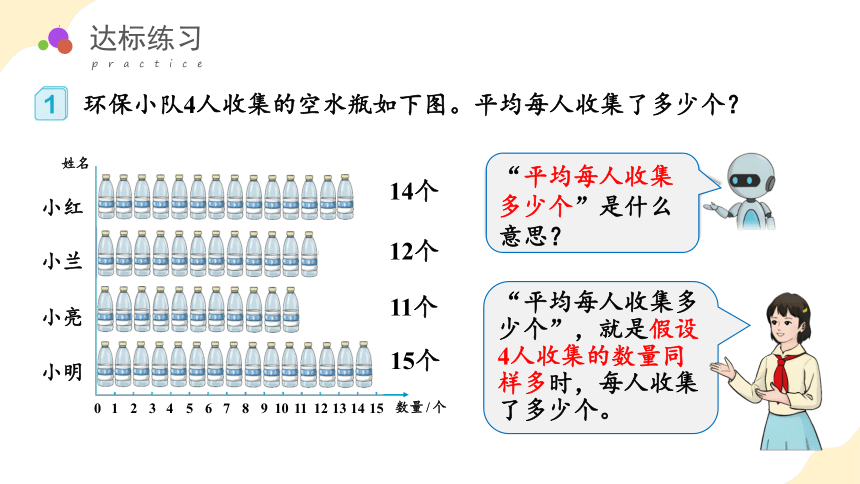
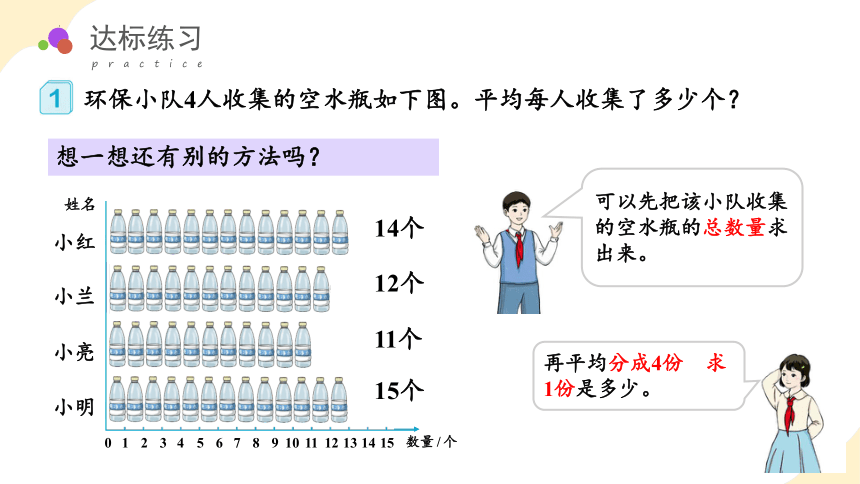
环保小队4人收集的空水瓶如下图。平均每人收集了多少个?
从图中,你知道哪些数学信息?
“平均每人收集多少个”是什么意思?
小红
小兰
小亮
小明
姓名
数量 / 个
0
2
1
6
3
4
5
7
8
11
10
9
12
13
14
15
14个
12个
11个
15个
“平均每人收集多少个”,就是假设4人收集的数量同样多时,每人收集了多少个。
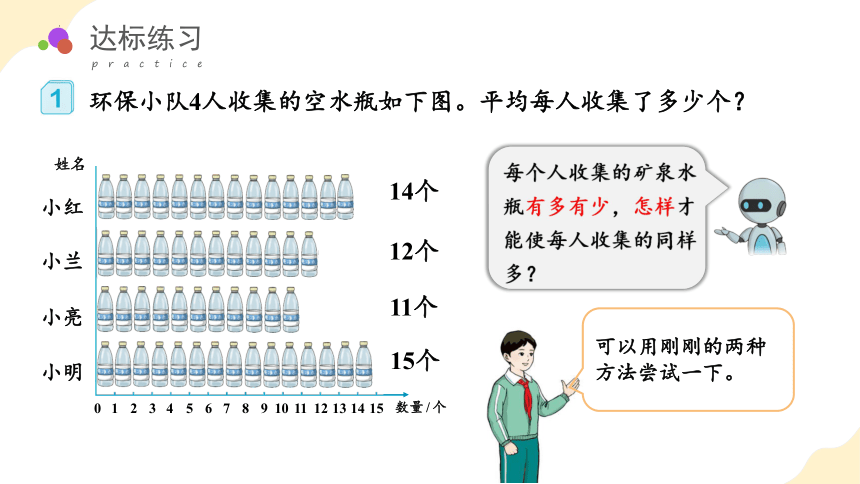
环保小队4人收集的空水瓶如下图。平均每人收集了多少个?
每个人收集的矿泉水瓶有多有少,怎样才能使每人收集的同样多?
小红
小兰
小亮
小明
姓名
数量 / 个
0
2
1
6
3
4
5
7
8
11
10
9
12
13
14
15
14个
12个
11个
15个
可以用刚刚的两种方法尝试一下。
14个
13个
小红比小兰多2个,可以给小兰1个。
姓名
数量 / 个
0
2
1
6
3
4
5
7
8
11
10
9
12
13
14
15
13个
13个
13个
小明比小亮多4个,可以给小亮2个。
这个相等的数据就是这组的平均数
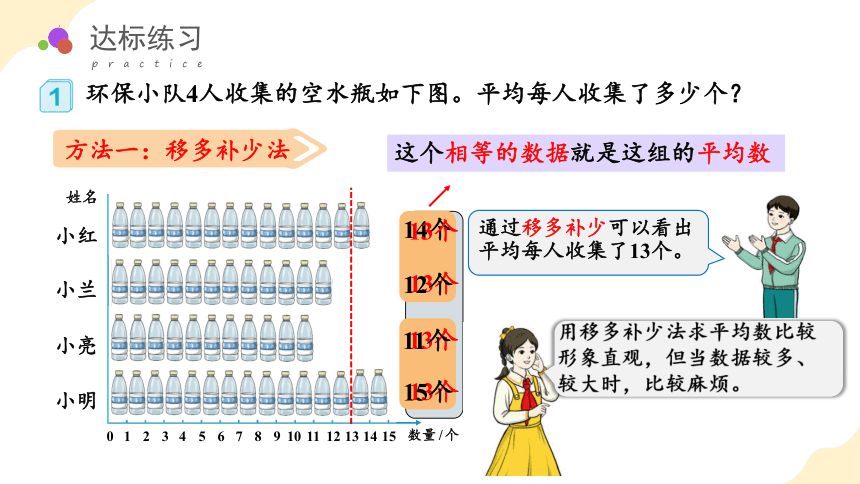
方法一:移多补少法
12个
11个
15个
小红
小兰
小亮
小明
环保小队4人收集的空水瓶如下图。平均每人收集了多少个?
通过移多补少可以看出平均每人收集了13个。
用移多补少法求平均数比较形象直观,但当数据较多、较大时,比较麻烦。
姓名
数量 / 个
0
2
1
6
3
4
5
7
8
11
10
9
12
13
14
15
小红
小兰
小亮
小明
环保小队4人收集的空水瓶如下图。平均每人收集了多少个?
14个
12个
11个
15个
想一想还有别的方法吗?
可以先把该小队收集的空水瓶的总数量求出来。
再平均分成4份,求1份是多少。
姓名
数量 / 个
0
2
1
6
3
4
5
7
8
11
10
9
12
13
14
15
小红
小兰
小亮
小明
环保小队4人收集的空水瓶如下图。平均每人收集了多少个?
14个
12个
11个
15个
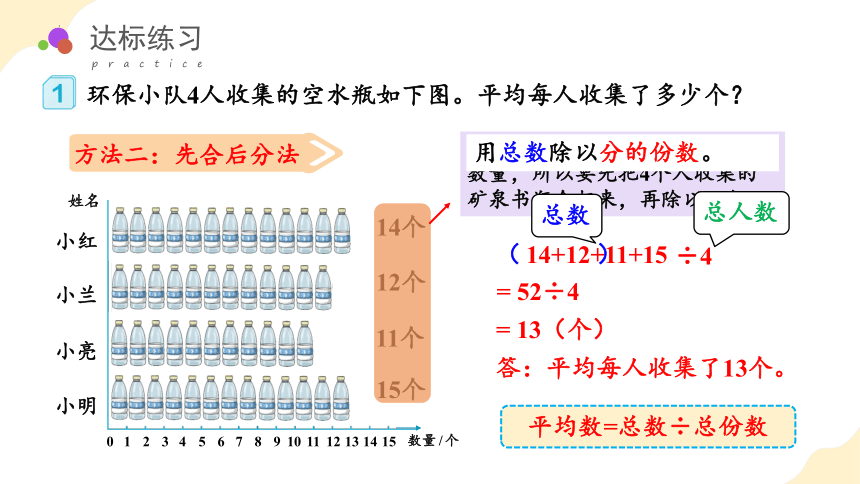
统计图中只给出了每个人收集的数量,所以要先把4个人收集的矿泉书瓶合起来,再除以人数。
用总数除以分的份数。
14+12+11+15
( )
÷4
= 52÷4
总数
= 13(个)
总人数
平均数=总数÷总份数
方法二:先合后分法
答:平均每人收集了13个。
小组讨论:“13”这个平均数量是每个学生收集到空水瓶的实际数量吗
“13”是这一组数据的平均数,平均数是一组数据平均水平的代表,而不是具体的某一个数据。
“13”并不是每个学生收集到的空水瓶的实际数量,而是“相当于”把4个学生收集到的瓶子总数平均分成4份。
有的学生收集到的瓶子数量比这个数量多,有的比这个数量少。
平均数不是一个实际的数,而是借助平均分的意义通过计算得到反应一组数据整体情况的一个“虚拟”的数。
一般情况下,平均数介于一组数据的最大值和最小值之间。
一组数据的和除以这组数据的个数所得的商就是平均数。
什么是平均数呢?平均数有什么特征?
区分“平均分”和“平均数”
(1)把15支铅笔平均分给3个小朋友,每个小朋友分得5支铅笔。
这里的5支表示平均分的结果,是每个小朋友实际分得的支数。
(2)3个小朋友一共有15支铅笔,平均每个孩子有5支铅笔。
这里的5支是平均数,它并不代表每人一定有5支铅笔。
用平均数进行不同组数据的比较
下面是第4小组男生队和女生队踢毽比赛的成绩。
哪个队的成绩更好一些?
下面是第4小组男生队和女生队踢毽比赛的成绩。
男生队的踢得最高的是20 个,女生也是20个。
两个队的人数不同,每个人的成绩也不同。
不再是两个数的比较,而是两组数据,怎样比较呢?
下面是第4小组男生队和女生队踢毽比赛的成绩。
可以一个一个比较吗?
19>18
15<20
16<19
20>19
15没有可以比较的数
只是比较某两个人的成绩,并不能代表整组的成绩,而且每组都有成绩好的和不好的,不能代表整个队。
下面是第4小组男生队和女生队踢毽比赛的成绩。
可以比较总数吗?总数不就能代表整体吗?
男生:19+15+16+20+15=85(个)
女生:18+20+19+19=76(个)
85个>76个
×
这样不公平,男生队的人数多,总数大。
下面是第4小组男生队和女生队踢毽比赛的成绩。
人数不同怎么比呢?
可以用每队的平均成绩来比较吗?
比较平均成绩实际上就是比较两队“平均每人踢了多少个”,不受两队人数的影响。
下面是第4小组男生队和女生队踢毽比赛的成绩。
男生:
(19+15+16+20+15)÷5
=85÷5
=17(个)
女生:
(18+20+19+19)÷4
=76÷4
=19(个)
17<19
答:女生队的成绩更好。
当两组同类数据的个数不同时,用平均数比较两组数据的总体情况比较合适。
如果男生队再增加1人,还能用平均数比较哪个队的成绩好吗?
如果男生队再增加1人,男生队人数比女生队人数更多,还是用平均数比较各队的成绩更公平。
如果女生队再增加1人,如何比较哪个队成绩好呢?
如果女生队再增加1人,两队人数一样多,此时可以比较每个队踢毽的总个数,也可以比较两个队的平均成绩。
达标练习,巩固成果
1. 下面是5名学生捐书的情况。
姓名 杨亮 王 波 刘飞 张 丽 唐小东
本数 8 6 9 8 14
平均每人捐了几本?
(8+6+9+8+14)÷5
=45÷5
=9(本)
答:平均每人捐了9本。
平均数=总数÷总份数
2. 下是李红同学记录的一周气温情况,根据记录填写下表并计算。
记录本地一周的气温,再计算出一周平均最高气温和最低气温。
2. 下是李红同学记录的一周气温情况,根据记录填写下表并计算。
记录本地一周的气温,再计算出一周平均最高气温和最低气温。
平均最高:
(21+21+22+24+22+21+23)÷7
=154÷7
=22(℃)
平均最低:
(10+10+12+12+11+11+11)÷7
=77÷7
=11(℃)
3.下面是小明周一至周五上学所花时间的情况。
星期 一 二 三 四 五
时间/分 15 17 14 16 18
小明平均每天上学要花多少时间?
(15+17+14+16+18)÷5
=80÷5
=16(分)
答:小明平均每天上学要花16分钟。
教材第89页“练习二十二”第2题
4.下面的说法正确吗?正确的画“√”,错误的画“×”。
(1)王悦5次跳远的总成绩是10m,她每次跳远的成绩肯定都 是2m。 ( )
(2)某小学排球队队员的平均身高是160cm,有的队员身高可能超过160cm,有的队员身高可能不到160cm。 ( )
(3)小东所在小组同学的平均体重是36kg,小刚所在小组同学的平均体重是34kg,小东一定比小刚重。 ( )
×
√
×
5. 两个小组做仰卧起坐。
哪个小组的成绩好些?
第一小组:132÷4=33(个)
第二小组:155÷5=31(个)
因为33>31,所以第一小组的成绩好。
6. 某小组6名同学的身高和体重情况如下表。
姓 名 刘 华 李 明 高 风 陈 莉 王 兵 张 丽
身高∕cm 139 140 135 138 139 137
体重∕kg 34 38 35 34 36 33
请你算出这些同学的平均身高和平均体重各是多少。
平均身高:
(139+140+135+138+139+137)÷6
=828÷6
=138(kg)
平均体重:
(34+38+35+34+36+33)÷6
=210÷6
=35(kg)
7. 某水果店的草莓最近7天的销售情况如下图。
(8+12+11+9+10+9+11)÷7=10(千克)
(1)平均每天销售草莓多少千克
可以进10千克草莓。
(2)如果你是水果店的进货员,你准备为25日进多少千克草莓 说说你的想法。
在一组不同的数中,平均数比最大的数要小一些,比最小的数要大一些。
平均数能较好地反映一组数据的总体情况,可以用平均数比较两组或几组同类别数据的总体情况。但不能代表每个个体的实际情况。
平均数
1
2
平均数是一组数据平均水平的代表数值。
求平均数的方法:
移多补少法
先总后分法
数量较小时使用比较方便
平均数=总数÷总份数
平均数
3
4
1. 绘制本节课知识的思维导图;
2. 完成《分层作业》。
第1课时 平均数
小学数学·四年级(下)·RJ
增强与同伴交流的意识及体验运用所学知识解决问题的乐趣,增强学好数学的信心。
在具体的问题情境中,感受求平均数是解决一些实际问题的需要,通过操作体会平均数的意义,能计算简单数据的平均数。
经历用平均数解决简单生活问题的过程,进一步积累分析和处理数据的方法,发展统计观念,初步感知“移多补少”的数学思想。
理解平均数的意义,掌握求平均数的方法。
理解平均数的意义。
把概念的关键属性和学生的认知结构相联系,使学生掌握概念,并能总结方法。
要使每个笔筒放的铅笔同样多,可以怎样做?
铅 笔:15支
笔 筒:5个
15÷5=3(支)
每个笔筒放几支?
先将铅笔合起来再平均分。这种方法叫做先合再分法。
拿出1支放入此笔筒
拿出2支放入此笔筒
要使每个笔筒放的铅笔同样多,可以怎样做?
还可以怎样分?
数量多的给数量少的一些,使它们的数量变得一样多,这种方法叫做移多补少法。。
认识平均数
环保小队4人收集的空水瓶如下图。平均每人收集了多少个?
从图中,你知道哪些数学信息?
“平均每人收集多少个”是什么意思?
小红
小兰
小亮
小明
姓名
数量 / 个
0
2
1
6
3
4
5
7
8
11
10
9
12
13
14
15
14个
12个
11个
15个
“平均每人收集多少个”,就是假设4人收集的数量同样多时,每人收集了多少个。
环保小队4人收集的空水瓶如下图。平均每人收集了多少个?
每个人收集的矿泉水瓶有多有少,怎样才能使每人收集的同样多?
小红
小兰
小亮
小明
姓名
数量 / 个
0
2
1
6
3
4
5
7
8
11
10
9
12
13
14
15
14个
12个
11个
15个
可以用刚刚的两种方法尝试一下。
14个
13个
小红比小兰多2个,可以给小兰1个。
姓名
数量 / 个
0
2
1
6
3
4
5
7
8
11
10
9
12
13
14
15
13个
13个
13个
小明比小亮多4个,可以给小亮2个。
这个相等的数据就是这组的平均数
方法一:移多补少法
12个
11个
15个
小红
小兰
小亮
小明
环保小队4人收集的空水瓶如下图。平均每人收集了多少个?
通过移多补少可以看出平均每人收集了13个。
用移多补少法求平均数比较形象直观,但当数据较多、较大时,比较麻烦。
姓名
数量 / 个
0
2
1
6
3
4
5
7
8
11
10
9
12
13
14
15
小红
小兰
小亮
小明
环保小队4人收集的空水瓶如下图。平均每人收集了多少个?
14个
12个
11个
15个
想一想还有别的方法吗?
可以先把该小队收集的空水瓶的总数量求出来。
再平均分成4份,求1份是多少。
姓名
数量 / 个
0
2
1
6
3
4
5
7
8
11
10
9
12
13
14
15
小红
小兰
小亮
小明
环保小队4人收集的空水瓶如下图。平均每人收集了多少个?
14个
12个
11个
15个
统计图中只给出了每个人收集的数量,所以要先把4个人收集的矿泉书瓶合起来,再除以人数。
用总数除以分的份数。
14+12+11+15
( )
÷4
= 52÷4
总数
= 13(个)
总人数
平均数=总数÷总份数
方法二:先合后分法
答:平均每人收集了13个。
小组讨论:“13”这个平均数量是每个学生收集到空水瓶的实际数量吗
“13”是这一组数据的平均数,平均数是一组数据平均水平的代表,而不是具体的某一个数据。
“13”并不是每个学生收集到的空水瓶的实际数量,而是“相当于”把4个学生收集到的瓶子总数平均分成4份。
有的学生收集到的瓶子数量比这个数量多,有的比这个数量少。
平均数不是一个实际的数,而是借助平均分的意义通过计算得到反应一组数据整体情况的一个“虚拟”的数。
一般情况下,平均数介于一组数据的最大值和最小值之间。
一组数据的和除以这组数据的个数所得的商就是平均数。
什么是平均数呢?平均数有什么特征?
区分“平均分”和“平均数”
(1)把15支铅笔平均分给3个小朋友,每个小朋友分得5支铅笔。
这里的5支表示平均分的结果,是每个小朋友实际分得的支数。
(2)3个小朋友一共有15支铅笔,平均每个孩子有5支铅笔。
这里的5支是平均数,它并不代表每人一定有5支铅笔。
用平均数进行不同组数据的比较
下面是第4小组男生队和女生队踢毽比赛的成绩。
哪个队的成绩更好一些?
下面是第4小组男生队和女生队踢毽比赛的成绩。
男生队的踢得最高的是20 个,女生也是20个。
两个队的人数不同,每个人的成绩也不同。
不再是两个数的比较,而是两组数据,怎样比较呢?
下面是第4小组男生队和女生队踢毽比赛的成绩。
可以一个一个比较吗?
19>18
15<20
16<19
20>19
15没有可以比较的数
只是比较某两个人的成绩,并不能代表整组的成绩,而且每组都有成绩好的和不好的,不能代表整个队。
下面是第4小组男生队和女生队踢毽比赛的成绩。
可以比较总数吗?总数不就能代表整体吗?
男生:19+15+16+20+15=85(个)
女生:18+20+19+19=76(个)
85个>76个
×
这样不公平,男生队的人数多,总数大。
下面是第4小组男生队和女生队踢毽比赛的成绩。
人数不同怎么比呢?
可以用每队的平均成绩来比较吗?
比较平均成绩实际上就是比较两队“平均每人踢了多少个”,不受两队人数的影响。
下面是第4小组男生队和女生队踢毽比赛的成绩。
男生:
(19+15+16+20+15)÷5
=85÷5
=17(个)
女生:
(18+20+19+19)÷4
=76÷4
=19(个)
17<19
答:女生队的成绩更好。
当两组同类数据的个数不同时,用平均数比较两组数据的总体情况比较合适。
如果男生队再增加1人,还能用平均数比较哪个队的成绩好吗?
如果男生队再增加1人,男生队人数比女生队人数更多,还是用平均数比较各队的成绩更公平。
如果女生队再增加1人,如何比较哪个队成绩好呢?
如果女生队再增加1人,两队人数一样多,此时可以比较每个队踢毽的总个数,也可以比较两个队的平均成绩。
达标练习,巩固成果
1. 下面是5名学生捐书的情况。
姓名 杨亮 王 波 刘飞 张 丽 唐小东
本数 8 6 9 8 14
平均每人捐了几本?
(8+6+9+8+14)÷5
=45÷5
=9(本)
答:平均每人捐了9本。
平均数=总数÷总份数
2. 下是李红同学记录的一周气温情况,根据记录填写下表并计算。
记录本地一周的气温,再计算出一周平均最高气温和最低气温。
2. 下是李红同学记录的一周气温情况,根据记录填写下表并计算。
记录本地一周的气温,再计算出一周平均最高气温和最低气温。
平均最高:
(21+21+22+24+22+21+23)÷7
=154÷7
=22(℃)
平均最低:
(10+10+12+12+11+11+11)÷7
=77÷7
=11(℃)
3.下面是小明周一至周五上学所花时间的情况。
星期 一 二 三 四 五
时间/分 15 17 14 16 18
小明平均每天上学要花多少时间?
(15+17+14+16+18)÷5
=80÷5
=16(分)
答:小明平均每天上学要花16分钟。
教材第89页“练习二十二”第2题
4.下面的说法正确吗?正确的画“√”,错误的画“×”。
(1)王悦5次跳远的总成绩是10m,她每次跳远的成绩肯定都 是2m。 ( )
(2)某小学排球队队员的平均身高是160cm,有的队员身高可能超过160cm,有的队员身高可能不到160cm。 ( )
(3)小东所在小组同学的平均体重是36kg,小刚所在小组同学的平均体重是34kg,小东一定比小刚重。 ( )
×
√
×
5. 两个小组做仰卧起坐。
哪个小组的成绩好些?
第一小组:132÷4=33(个)
第二小组:155÷5=31(个)
因为33>31,所以第一小组的成绩好。
6. 某小组6名同学的身高和体重情况如下表。
姓 名 刘 华 李 明 高 风 陈 莉 王 兵 张 丽
身高∕cm 139 140 135 138 139 137
体重∕kg 34 38 35 34 36 33
请你算出这些同学的平均身高和平均体重各是多少。
平均身高:
(139+140+135+138+139+137)÷6
=828÷6
=138(kg)
平均体重:
(34+38+35+34+36+33)÷6
=210÷6
=35(kg)
7. 某水果店的草莓最近7天的销售情况如下图。
(8+12+11+9+10+9+11)÷7=10(千克)
(1)平均每天销售草莓多少千克
可以进10千克草莓。
(2)如果你是水果店的进货员,你准备为25日进多少千克草莓 说说你的想法。
在一组不同的数中,平均数比最大的数要小一些,比最小的数要大一些。
平均数能较好地反映一组数据的总体情况,可以用平均数比较两组或几组同类别数据的总体情况。但不能代表每个个体的实际情况。
平均数
1
2
平均数是一组数据平均水平的代表数值。
求平均数的方法:
移多补少法
先总后分法
数量较小时使用比较方便
平均数=总数÷总份数
平均数
3
4
1. 绘制本节课知识的思维导图;
2. 完成《分层作业》。
