第七单元_第09课时_加减法的估算(教学课件)-二年级数学下册人教版 (共26张PPT)
文档属性
| 名称 | 第七单元_第09课时_加减法的估算(教学课件)-二年级数学下册人教版 (共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 7.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-11 18:51:34 | ||
图片预览






文档简介
(共26张PPT)
小学数学·二年级(下)·RJ
第9课时 解决问题(估算)
经历探究过程,体会估算方法的多样化,初步培养数感、估算意识和估算能力。
结合具体情境初步学会用加减法估算解决问题。
在解决问题的过程中,感受数学知识与日常生活的联系,初步感受估算的价值。
在具体的情境中学会用整百、整千数加减法估算解决问题。
体验估算的多样化,能根据具体情境选择适当的估算策略。
培养数感、估算意识和估算能力。促进学生核心素养的发展。
1. 口算。
200+300=
900-500=
500
400
400+100=
600-500=
500
100
300+300=
1000-600=
600
400
1000+8000=
7000-2000=
9000
5000
请说说你是怎样算的?
2. 填一填。
(1)我们学校四年级一共有608名学生,大约有( )人。
(2)学校图书馆共有书籍3890本,约是( )本。
(3) 豆豆一分钟跳绳可以跳109个,约是( )个。
600
4000
100
阅读分析题意,探索解决方法
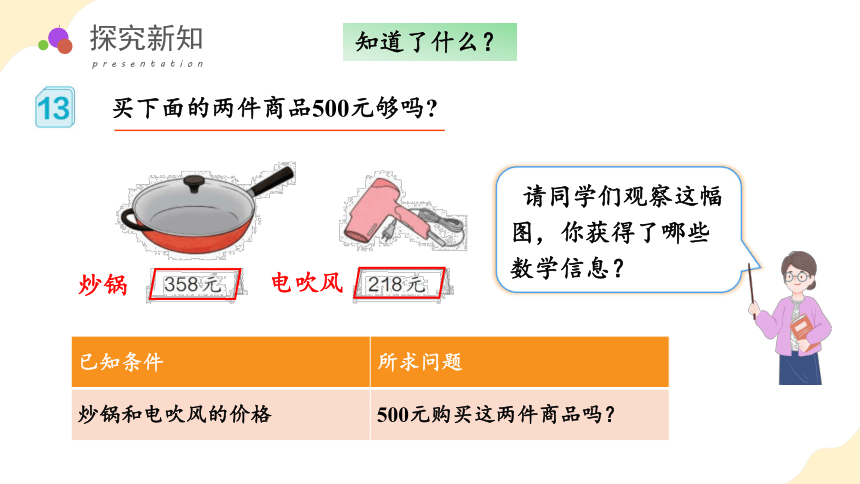
买下面的两件商品500元够吗
请同学们观察这幅图,你获得了哪些数学信息?
炒锅
电吹风
知道了什么?
已知条件 所求问题
炒锅和电吹风的价格 500元购买这两件商品吗?
“买这两件商品,500元够吗?”这个问题该如何解决呢?说说你的想法。
要知道500元够不够,先要知道买炒锅和电吹风一共得付多少钱。
怎样解答?
可以通过估算判断。
那就是需要计算358+218,还没学到?
买右边的两件商品500元够吗
要估计两个商品之和,可以怎样想?
怎样解答?
如何估算呢?
与同桌说你的想法。
运用估算解决问题
买右边的两件商品500元够吗
怎样解答?
358+218 ≈
炒锅超过了300元,电吹风超过了200元,300+200=500,带500元肯定不够。
358>300 218>200
300+200=500
带500元不够。
买右边的两件商品500元够吗
怎样解答?
358+218 ≈
找近似数,把358估作360,218估作220,360+220=580(元) ,580>500,所以不够。
还可以怎样想?
买右边的两件商品500元够吗
怎样解答?
358+218 ≈
找近似数,把358估作360,218估作220,360+220=580(元) ,580>500,所以不够。
估计正确吗?
解答正确吗?
500元买了300多元的炒锅,剩下不到200元,肯定不够买吹风机。
即使炒锅300元,500-300=200,剩下的钱也不够买吹风机!
买右边的两件商品500元够吗
延伸拓展
想一想带700元够吗
那可以把烧锅358看成400,把电吹风218看成200吗?
炒锅不到400元,
电吹风不到300元。
400+300=700,
带700元肯定够。
不能,因为一个多看了,一个少看了,这样不好确定。
归纳总结
请同学们结合刚才的分析说说怎样用估算解决生活中的实际问题?
可以用估算的方法,先找到合适的近似数,再用近似数口算,最后判断能否解决问题。
估算时,近似数的取值可大可小,要根据具体情况而定。
达标练习,巩固成果
1.估一估。
209+394 ≈
600
459+1290 ≈
1800
896-394 ≈
500
7009+970 ≈
8000
966+592 ≈
1600
2199+351 ≈
2600
2.演播厅有1000个座位,城关小学准备组织一、二年级的同学去看电影。一年级有589人,二年级有361人。两个年级同时去,能坐下吗?
可以这样想:
一年级不到600人,
二年级不到400人,
600+400=( )人,
所以( )坐下。
还可以这样想:
一年级不到600人,
1000-600=( )人,
二年级不到( )人,
所以( )坐下。
1000
能
400
400
能
368元
300+400=700(元)
溜冰鞋不到300元
一双溜冰鞋和一辆童车一共不到700元,
3.妈妈准备给笑笑买一双溜冰鞋和一辆童车。妈妈带700元够吗?
答:妈妈带700元够。
90元
189元
298元
童车不到400元
4.城关镇礼堂有3000个座位,城关镇的三所小学各有800多名学生。如果这三所小学的学生同时来礼堂参加活动,礼堂的座位够吗?
900+900+900
=2700
2700<3000
所以能坐下。
800多估成900
想一想: 这样能解决问题吗?为什么?
5. 有一条500厘米长的彩带,包扎三盒礼物已经用掉了300厘米,还需要240厘米做蝴蝶结。剩下的彩带够吗
500-300=200(厘米)
200<240
所以剩下的彩带不够。
6.广场举办消夏音乐会,需要租1500把椅子。
900+700=1600
1500<1600
答:够了。
解决生活中的实际问题时,我们可以用估算的方法,先找到合适的近似数,再用近似数口算,最后判断能否解决问题。
估算时,近似数的取值可大可小,要根据具体情况而定。
1. 利用加减法的估算解决生活中的实际问题;
2. 完成《分层作业》。
小学数学·二年级(下)·RJ
第9课时 解决问题(估算)
经历探究过程,体会估算方法的多样化,初步培养数感、估算意识和估算能力。
结合具体情境初步学会用加减法估算解决问题。
在解决问题的过程中,感受数学知识与日常生活的联系,初步感受估算的价值。
在具体的情境中学会用整百、整千数加减法估算解决问题。
体验估算的多样化,能根据具体情境选择适当的估算策略。
培养数感、估算意识和估算能力。促进学生核心素养的发展。
1. 口算。
200+300=
900-500=
500
400
400+100=
600-500=
500
100
300+300=
1000-600=
600
400
1000+8000=
7000-2000=
9000
5000
请说说你是怎样算的?
2. 填一填。
(1)我们学校四年级一共有608名学生,大约有( )人。
(2)学校图书馆共有书籍3890本,约是( )本。
(3) 豆豆一分钟跳绳可以跳109个,约是( )个。
600
4000
100
阅读分析题意,探索解决方法
买下面的两件商品500元够吗
请同学们观察这幅图,你获得了哪些数学信息?
炒锅
电吹风
知道了什么?
已知条件 所求问题
炒锅和电吹风的价格 500元购买这两件商品吗?
“买这两件商品,500元够吗?”这个问题该如何解决呢?说说你的想法。
要知道500元够不够,先要知道买炒锅和电吹风一共得付多少钱。
怎样解答?
可以通过估算判断。
那就是需要计算358+218,还没学到?
买右边的两件商品500元够吗
要估计两个商品之和,可以怎样想?
怎样解答?
如何估算呢?
与同桌说你的想法。
运用估算解决问题
买右边的两件商品500元够吗
怎样解答?
358+218 ≈
炒锅超过了300元,电吹风超过了200元,300+200=500,带500元肯定不够。
358>300 218>200
300+200=500
带500元不够。
买右边的两件商品500元够吗
怎样解答?
358+218 ≈
找近似数,把358估作360,218估作220,360+220=580(元) ,580>500,所以不够。
还可以怎样想?
买右边的两件商品500元够吗
怎样解答?
358+218 ≈
找近似数,把358估作360,218估作220,360+220=580(元) ,580>500,所以不够。
估计正确吗?
解答正确吗?
500元买了300多元的炒锅,剩下不到200元,肯定不够买吹风机。
即使炒锅300元,500-300=200,剩下的钱也不够买吹风机!
买右边的两件商品500元够吗
延伸拓展
想一想带700元够吗
那可以把烧锅358看成400,把电吹风218看成200吗?
炒锅不到400元,
电吹风不到300元。
400+300=700,
带700元肯定够。
不能,因为一个多看了,一个少看了,这样不好确定。
归纳总结
请同学们结合刚才的分析说说怎样用估算解决生活中的实际问题?
可以用估算的方法,先找到合适的近似数,再用近似数口算,最后判断能否解决问题。
估算时,近似数的取值可大可小,要根据具体情况而定。
达标练习,巩固成果
1.估一估。
209+394 ≈
600
459+1290 ≈
1800
896-394 ≈
500
7009+970 ≈
8000
966+592 ≈
1600
2199+351 ≈
2600
2.演播厅有1000个座位,城关小学准备组织一、二年级的同学去看电影。一年级有589人,二年级有361人。两个年级同时去,能坐下吗?
可以这样想:
一年级不到600人,
二年级不到400人,
600+400=( )人,
所以( )坐下。
还可以这样想:
一年级不到600人,
1000-600=( )人,
二年级不到( )人,
所以( )坐下。
1000
能
400
400
能
368元
300+400=700(元)
溜冰鞋不到300元
一双溜冰鞋和一辆童车一共不到700元,
3.妈妈准备给笑笑买一双溜冰鞋和一辆童车。妈妈带700元够吗?
答:妈妈带700元够。
90元
189元
298元
童车不到400元
4.城关镇礼堂有3000个座位,城关镇的三所小学各有800多名学生。如果这三所小学的学生同时来礼堂参加活动,礼堂的座位够吗?
900+900+900
=2700
2700<3000
所以能坐下。
800多估成900
想一想: 这样能解决问题吗?为什么?
5. 有一条500厘米长的彩带,包扎三盒礼物已经用掉了300厘米,还需要240厘米做蝴蝶结。剩下的彩带够吗
500-300=200(厘米)
200<240
所以剩下的彩带不够。
6.广场举办消夏音乐会,需要租1500把椅子。
900+700=1600
1500<1600
答:够了。
解决生活中的实际问题时,我们可以用估算的方法,先找到合适的近似数,再用近似数口算,最后判断能否解决问题。
估算时,近似数的取值可大可小,要根据具体情况而定。
1. 利用加减法的估算解决生活中的实际问题;
2. 完成《分层作业》。
