专题16 图形认识初步(选择题30题)(含解析)-【冲刺2023中考】真题冲刺专题(知识点+专题训练)
文档属性
| 名称 | 专题16 图形认识初步(选择题30题)(含解析)-【冲刺2023中考】真题冲刺专题(知识点+专题训练) |  | |
| 格式 | doc | ||
| 文件大小 | 636.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-12 09:50:26 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
【真题汇编】2023年中考数学备考之图形认识初步
1.认识立体图形
(1)几何图形:从实物中抽象出的各种图形叫几何图形.几何图形分为立体图形和平面图形.
(2)立体图形:有些几何图形(如长方体、正方体、圆柱、圆锥、球等)的各部分不都在同一个平面内,这就是立体图形.
(3)重点和难点突破:
结合实物,认识常见的立体图形,如:长方体、正方体、圆柱、圆锥、球、棱柱、棱锥等.能区分立体图形与平面图形,立体图形占有一定空间,各部分不都在同一平面内.
2.几何体的展开图
(1)多数立体图形是由平面图形围成的.沿着棱剪开就得到平面图形,这样的平面图形就是相应立体图形的展开图.同一个立体图形按不同的方式展开,得到的平面展开图是不一样的,同时也可看出,立体图形的展开图是平面图形.
(2)常见几何体的侧面展开图:
①圆柱的侧面展开图是长方形.②圆锥的侧面展开图是扇形.③正方体的侧面展开图是长方形.④三棱柱的侧面展开图是长方形.
(3)立体图形的侧面展开图,体现了平面图形与立体图形的联系.立体图形问题可以转化为平面图形问题解决.
从实物出发,结合具体的问题,辨析几何体的展开图,通过结合立体图形与平面图形的转化,建立空间观念,是解决此类问题的关键.
3.展开图折叠成几何体
通过结合立体图形与平面图形的相互转化,去理解和掌握几何体的展开图,要注意多从实物出发,然后再从给定的图形中辨认它们能否折叠成给定的立体图形.
4.专题:正方体相对两个面上的文字
(1)对于此类问题一般方法是用纸按图的样子折叠后可以解决,或是在对展开图理解的基础上直接想象.
(2)从实物出发,结合具体的问题,辨析几何体的展开图,通过结合立体图形与平面图形的转化,建立空间观念,是解决此类问题的关键.
(3)正方体的展开图有11种情况,分析平面展开图的各种情况后再认真确定哪两个面的对面.
5.截一个几何体
(1)截面:用一个平面去截一个几何体,截出的面叫做截面.
(2)截面的形状随截法的不同而改变,一般为多边形或圆,也可能是不规则图形,一般的截面与几何体的几个面相交就得到几条交线,截面就是几边形,因此,若一个几何体有几个面,则截面最多为几边形.
6.线段的性质:两点之间线段最短
线段公理
两点的所有连线中,可以有无数种连法,如折线、曲线、线段等,这些所有的线中,线段最短.
简单说成:两点之间,线段最短.
7.方向角
方向角是从正北或正南方向到目标方向所形成的小于90°的角
(1)方向角是表示方向的角;以正北,正南方向为基准,来描述物体所处的方向.
(2)用方向角描述方向时,通常以正北或正南方向为角的始边,以对象所处的射线为终边,故描述方向角时,一般先叙述北或南,再叙述偏东或偏西.(注意几个方向的角平分线按日常习惯,即东北,东南,西北,西南.)
(3)画方向角
以正南或正北方向作方向角的始边,另一边则表示对象所处的方向的射线.
8.度分秒的换算
(1)度、分、秒是常用的角的度量单位.1度=60分,即1°=60′,1分=60秒,即1′=60″.
(2)具体换算可类比时钟上的时、分、秒来说明角的度量单位度、分、秒之间也是60进制,将高级单位化为低级单位时,乘以60,反之,将低级单位转化为高级单位时除以60.同时,在进行度、分、秒的运算时也应注意借位和进位的方法.
9.余角和补角
(1)余角:如果两个角的和等于90°(直角),就说这两个角互为余角.即其中一个角是另一个角的余角.
(2)补角:如果两个角的和等于180°(平角),就说这两个角互为补角.即其中一个角是另一个角的补角.
(3)性质:等角的补角相等.等角的余角相等.
(4)余角和补角计算的应用,常常与等式的性质、等量代换相关联.
注意:余角(补角)与这两个角的位置没有关系.不论这两个角在哪儿,只要度数之和满足了定义,则它们就具备相应的关系.
【真题汇编】2023年中考数学备考之图形认识初步
(选择题30题)
满分:120分 建议时间:100分钟
学校:___________姓名:___________班级:___________考号:___________
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息2.请将答案正确填写在答题卡上
一.选择题(共30小题,满分120分,每小题4分)
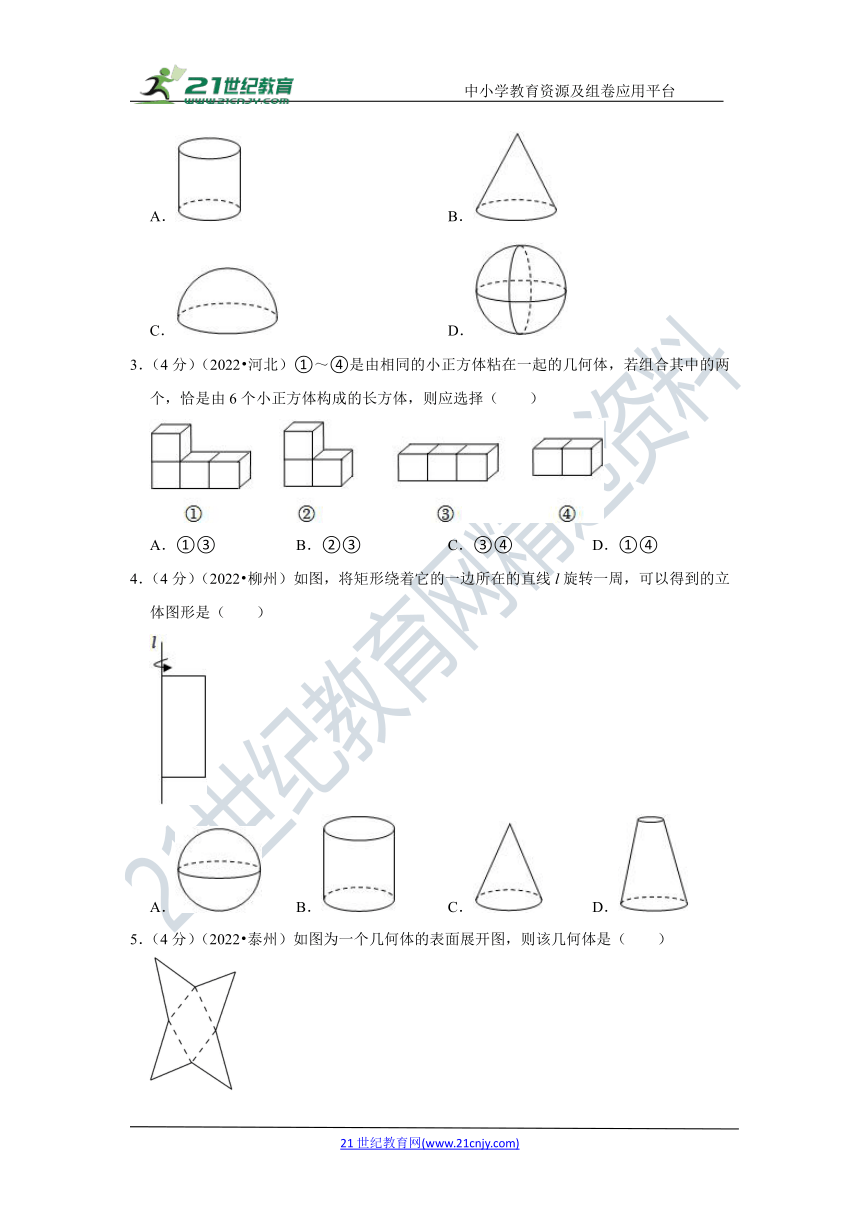
1.(4分)(2022 北京)下面几何体中,是圆锥的为( )
A. B.
C. D.
2.(4分)(2022 自贡)如图,将矩形纸片ABCD绕边CD所在直线旋转一周,得到的立体图形是( )
A. B.
C. D.
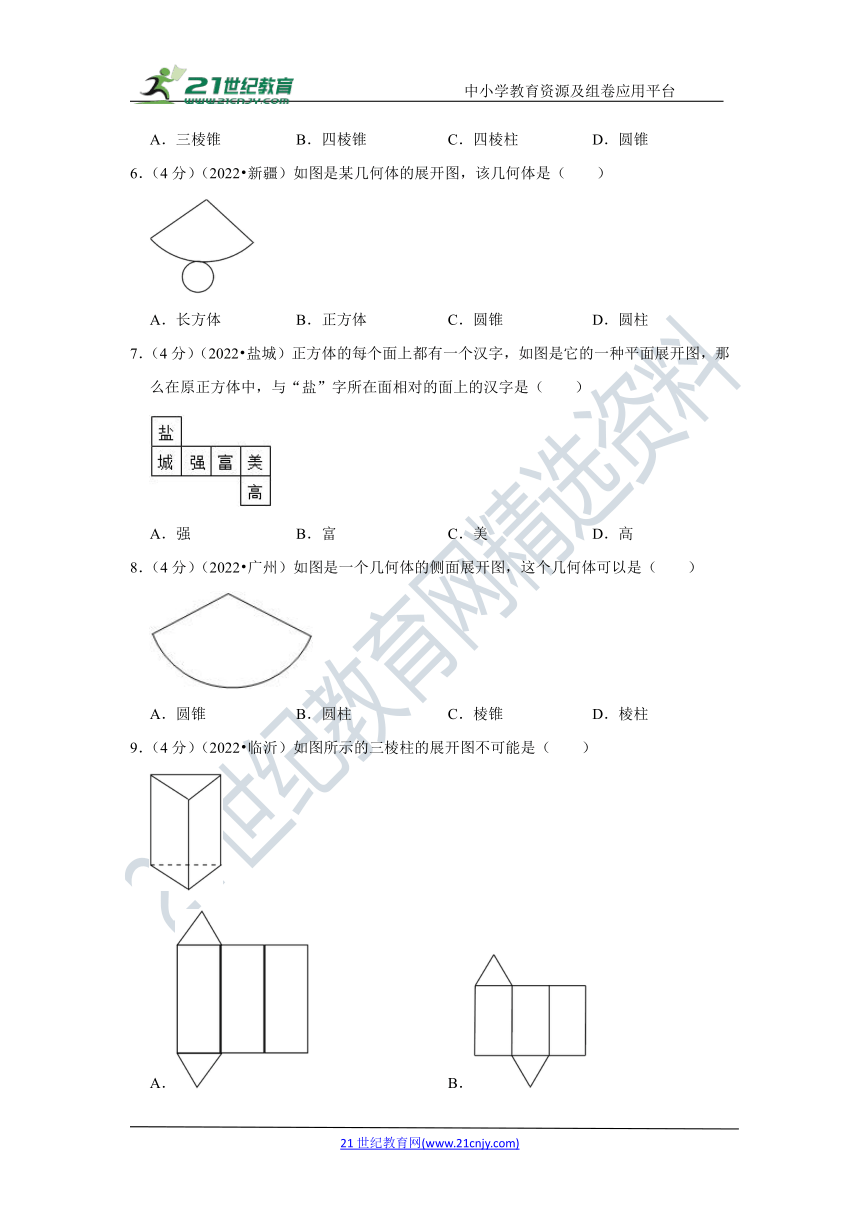
3.(4分)(2022 河北)①~④是由相同的小正方体粘在一起的几何体,若组合其中的两个,恰是由6个小正方体构成的长方体,则应选择( )
A.①③ B.②③ C.③④ D.①④
4.(4分)(2022 柳州)如图,将矩形绕着它的一边所在的直线l旋转一周,可以得到的立体图形是( )
A. B. C. D.
5.(4分)(2022 泰州)如图为一个几何体的表面展开图,则该几何体是( )
A.三棱锥 B.四棱锥 C.四棱柱 D.圆锥
6.(4分)(2022 新疆)如图是某几何体的展开图,该几何体是( )
A.长方体 B.正方体 C.圆锥 D.圆柱
7.(4分)(2022 盐城)正方体的每个面上都有一个汉字,如图是它的一种平面展开图,那么在原正方体中,与“盐”字所在面相对的面上的汉字是( )
A.强 B.富 C.美 D.高
8.(4分)(2022 广州)如图是一个几何体的侧面展开图,这个几何体可以是( )
A.圆锥 B.圆柱 C.棱锥 D.棱柱
9.(4分)(2022 临沂)如图所示的三棱柱的展开图不可能是( )
A. B.
C. D.
10.(4分)(2022 广元)如图是某几何体的展开图,该几何体是( )
A.长方体 B.圆柱 C.圆锥 D.三棱柱
11.(4分)(2021 巴中)某立体图形的表面展开图如图所示,这个立体图形是( )
A. B. C. D.
12.(4分)(2022 常州)下列图形中,为圆柱的侧面展开图的是( )
A. B.
C. D.
13.(4分)(2022 绥化)下列图形中,正方体展开图错误的是( )
A. B.
C. D.
14.(4分)(2022 岳阳)某个立体图形的侧面展开图如图所示,它的底面是正三角形,那么这个立体图形是( )
A.圆柱 B.圆锥 C.三棱柱 D.四棱柱
15.(4分)(2022 宿迁)下列展开图中,是正方体展开图的是( )
A. B.
C. D.
16.(4分)(2022 台湾)如图为一个长方体的展开图,且长方体的底面为正方形.根据图中标示的长度,求此长方体的体积为何?( )
A.144 B.224 C.264 D.300
17.(4分)(2022 六盘水)如图,裁掉一个正方形后能折叠成正方体,但不能裁掉的是( )
A.① B.② C.③ D.④
18.(4分)(2022 遂宁)如图是正方体的一种展开图,那么在原正方体中与“我”字所在面相对的面上的汉字是( )
A.大 B.美 C.遂 D.宁
19.(4分)(2022 徐州)如图,已知骰子相对两面的点数之和为7,下列图形为该骰子表面展开图的是( )
A. B.
C. D.
20.(4分)(2022 资阳)如图是正方体的表面展开图,每个面内都分别写有一个字,则与“创”字相对面上的字是( )
A.文 B.明 C.城 D.市
21.(4分)(2022 内江)如图是正方体的表面展开图,则与“话”字相对的字是( )
A.跟 B.党 C.走 D.听
22.(4分)(2022 枣庄)某正方体的每个面上都有一个汉字,如图是它的一种展开图,那么在原正方体中,与“亮”字所在面相对的面上的汉字是( )
A.青 B.春 C.梦 D.想
23.(4分)(2021 黔西南州)如图是一个正方体的展开图,把它折叠成正方体后,有“学”字一面的相对面上的字是( )
A.雷 B.锋 C.精 D.神
24.(4分)(2022 淄博)经过折叠可以围成正方体,且在正方体侧面上的字恰好环绕组成一个四字成语的图形是( )
A. B.
C. D.
25.(4分)(2022 贵阳)如图,用一个平行于圆锥底面的平面截圆锥,截面的形状是( )
A. B.
C. D.
26.(4分)(2022 柳州)如图,从学校A到书店B有①、②、③、④四条路线,其中最短的路线是( )
A.① B.② C.③ D.④
27.(4分)(2022 烟台)如图,某海域中有A,B,C三个小岛,其中A在B的南偏西40°方向,C在B的南偏东35°方向,且B,C到A的距离相等,则小岛C相对于小岛A的方向是( )
A.北偏东70° B.北偏东75° C.南偏西70° D.南偏西20°
28.(4分)(2022 甘肃)若∠A=40°,则∠A的余角的大小是( )
A.50° B.60° C.140° D.160°
29.(4分)(2021 百色)已知∠α=25°30′,则它的余角为( )
A.25°30′ B.64°30′ C.74°30′ D.154°30′
30.(4分)(2022 台湾)缓降机是火灾发生时避难的逃生设备,如图是厂商提供的缓降机安装示意图,图中呈现在三楼安装缓降机时,使用此缓降机直接缓降到一楼地面的所需绳长(不计安全带).若某栋建筑的每个楼层高度皆为3公尺,则根据如图的安装方式在该建筑八楼安装缓降机时,使用此缓降机直接缓降到一楼地面的所需绳长(不计安全带)为多少公尺?( )
A.21.7 B.22.6 C.24.7 D.25.6
【真题汇编】2023年中考数学备考之图形认识初步(选择题30题)
参考答案与试题解析
一.选择题(共30小题,满分120分,每小题4分)
1.(4分)(2022 北京)下面几何体中,是圆锥的为( )
A. B.
C. D.
【解析】解:A是圆柱;
B是圆锥;
C是三棱锥,也叫四面体;
D是球体,简称球;
故选:B.
2.(4分)(2022 自贡)如图,将矩形纸片ABCD绕边CD所在直线旋转一周,得到的立体图形是( )
A. B.
C. D.
【解析】解:根据“点动成线,线动成面,面动成体”,
将矩形纸片ABCD绕边CD所在直线旋转一周,所得到的立体图形是圆柱.
故选:A.
3.(4分)(2022 河北)①~④是由相同的小正方体粘在一起的几何体,若组合其中的两个,恰是由6个小正方体构成的长方体,则应选择( )
A.①③ B.②③ C.③④ D.①④
【解析】解:由题意知,组合后的几何体是长方体且由6个小正方体构成,
∴①④符合要求,
故选:D.
4.(4分)(2022 柳州)如图,将矩形绕着它的一边所在的直线l旋转一周,可以得到的立体图形是( )
A. B. C. D.
【解析】解:将矩形绕着它的一边所在的直线l旋转一周,可以得到圆柱体,
故选:B.
5.(4分)(2022 泰州)如图为一个几何体的表面展开图,则该几何体是( )
A.三棱锥 B.四棱锥 C.四棱柱 D.圆锥
【解析】解:根据展开图可以得出是四棱锥的展开图,
故选:B.
6.(4分)(2022 新疆)如图是某几何体的展开图,该几何体是( )
A.长方体 B.正方体 C.圆锥 D.圆柱
【解析】解:根据展开图得该几何体是圆锥,
故选:C.
7.(4分)(2022 盐城)正方体的每个面上都有一个汉字,如图是它的一种平面展开图,那么在原正方体中,与“盐”字所在面相对的面上的汉字是( )
A.强 B.富 C.美 D.高
【解析】解:正方体的表面展开图相对的面之间一定相隔一个正方形,
“盐”与“高”是相对面,
“城”与“富”是相对面,
“强”与“美”是相对面,
故选:D.
8.(4分)(2022 广州)如图是一个几何体的侧面展开图,这个几何体可以是( )
A.圆锥 B.圆柱 C.棱锥 D.棱柱
【解析】解:∵圆锥的侧面展开图是扇形,
∴判断这个几何体是圆锥,
故选:A.
9.(4分)(2022 临沂)如图所示的三棱柱的展开图不可能是( )
A. B.
C. D.
【解析】解:如图所示的三棱柱的展开图不可能是;
故选:D.
10.(4分)(2022 广元)如图是某几何体的展开图,该几何体是( )
A.长方体 B.圆柱 C.圆锥 D.三棱柱
【解析】解:由两个圆和一个长方形可以围成圆柱,
故选:B.
11.(4分)(2021 巴中)某立体图形的表面展开图如图所示,这个立体图形是( )
A. B. C. D.
【解析】解:四个三角形和一个四边形,是四棱锥的组成,所以该立体图形的名称为四棱锥.
故选:A.
12.(4分)(2022 常州)下列图形中,为圆柱的侧面展开图的是( )
A. B.
C. D.
【解析】解:根据题意,把圆柱的侧面沿它的一条母线剪开展在一个平面上,
得到其侧面展开图是对边平行且相等的四边形;
又有母线垂直于上下底面,故可得是长方形.
故选:D.
13.(4分)(2022 绥化)下列图形中,正方体展开图错误的是( )
A. B.
C. D.
【解析】解:由展开图的知识可知,四个小正方形绝对不可能展开成田字形,故D选项都不符合题意.
故选:D.
14.(4分)(2022 岳阳)某个立体图形的侧面展开图如图所示,它的底面是正三角形,那么这个立体图形是( )
A.圆柱 B.圆锥 C.三棱柱 D.四棱柱
【解析】解:A选项,圆柱的底面是圆,故该选项不符合题意;
B选项,圆锥的底面是圆,故该选项不符合题意;
C选项,三棱柱的底面是三角形,侧面是三个长方形,故该选项符合题意;
D选项,四棱柱的底面是四边形,故该选项不符合题意;
故选:C.
15.(4分)(2022 宿迁)下列展开图中,是正方体展开图的是( )
A. B.
C. D.
【解析】解:由展开图的知识可知,四个小正方形绝对不可能展开成田字形,故A选项和D选项都不符合题意;
四个连成一排的小正方形可以围成前后左右四面,剩下的两面必须分在上下两面才能围成正方体,
故B选项不符合题意,C选项符合题意,
故选:C.
16.(4分)(2022 台湾)如图为一个长方体的展开图,且长方体的底面为正方形.根据图中标示的长度,求此长方体的体积为何?( )
A.144 B.224 C.264 D.300
【解析】解:设展开图的长方形的长为a,宽为b,
12=3b,2b+a=22,
解得a=14,b=4,
∴长方体的体积为:4×4×14=224,
故选:B.
17.(4分)(2022 六盘水)如图,裁掉一个正方形后能折叠成正方体,但不能裁掉的是( )
A.① B.② C.③ D.④
【解析】解:如图,裁掉一个正方形后能折叠成正方体,但不能裁掉的是①,
故选:A.
18.(4分)(2022 遂宁)如图是正方体的一种展开图,那么在原正方体中与“我”字所在面相对的面上的汉字是( )
A.大 B.美 C.遂 D.宁
【解析】解:由图可知,
我和美相对,爱和宁相对,大和遂相对,
故选:B.
19.(4分)(2022 徐州)如图,已知骰子相对两面的点数之和为7,下列图形为该骰子表面展开图的是( )
A. B.
C. D.
【解析】解:根据正方体的表面展开图,相对的面之间一定相隔一个正方形,
A、1点6点是相对面,3点与5点是相对面,2点与4点是相对面,所以不可以折成符合规则的骰子,故本选项不符合题意;
B、4点与3点是相对面,2点与6点是相对面,1点与5点是相对面,所以不可以折成符合规则的骰子,故本选项不符合题意;
C、3点与4点是相对面,2点与6点是相对面,1点与5点是相对面,所以不可以折成符合规则的骰子,故本选项不符合题意;
D、2点与5点是相对面,3点与4点是相对面,1点与6点是相对面,所以可以折成符合规则的骰子,故本选项符合题意.
故选:D.
20.(4分)(2022 资阳)如图是正方体的表面展开图,每个面内都分别写有一个字,则与“创”字相对面上的字是( )
A.文 B.明 C.城 D.市
【解析】解:将正方体的表面展开图还原成正方体,以“文”字为底,则左边的是“建”字,右边的是“明”字,上面的是“城”字,正面的是“市”字,后面的是“创”字,可知“创”字与“市”字相对.
故选:D.
21.(4分)(2022 内江)如图是正方体的表面展开图,则与“话”字相对的字是( )
A.跟 B.党 C.走 D.听
【解析】解:由正方体表面展开图的“相间、Z端是对面”可知,
“话”与“走”是对面,
故答案为:C.
22.(4分)(2022 枣庄)某正方体的每个面上都有一个汉字,如图是它的一种展开图,那么在原正方体中,与“亮”字所在面相对的面上的汉字是( )
A.青 B.春 C.梦 D.想
【解析】解:在原正方体中,与“亮”字所在面相对的面上的汉字是:想,
故选:D.
23.(4分)(2021 黔西南州)如图是一个正方体的展开图,把它折叠成正方体后,有“学”字一面的相对面上的字是( )
A.雷 B.锋 C.精 D.神
【解析】解:“学”与“神”是相对面,
“习”与“锋”是相对面,
“雷”与“精”是相对面.
故选:D.
24.(4分)(2022 淄博)经过折叠可以围成正方体,且在正方体侧面上的字恰好环绕组成一个四字成语的图形是( )
A. B.
C. D.
【解析】解:A、因为图中两个空白面不是相对面,所以图中的四个字不能恰好环绕组成一个四字成语,故A不符合题意;
B、因为图中两个空白面不是相对面,所以图中的四个字不能恰好环绕组成一个四字成语,故B不符合题意;
C、因为金与题是相对面,榜与名是相对面,所以正方体侧面上的字恰好环绕组成一个四字成语金榜题名,故C符合题意;
D、因为图中两个空白面不是相对面,所以图中的四个字不能恰好环绕组成一个四字成语,故D不符合题意;
故选:C.
25.(4分)(2022 贵阳)如图,用一个平行于圆锥底面的平面截圆锥,截面的形状是( )
A. B.
C. D.
【解析】解:用一个平行于圆锥底面的平面截圆锥,截面的形状是圆,
故选:B.
26.(4分)(2022 柳州)如图,从学校A到书店B有①、②、③、④四条路线,其中最短的路线是( )
A.① B.② C.③ D.④
【解析】解:根据题意可得,
从学校A到书店B有①、②、③、④四条路线,其中最短的路线是②.
故选:B.
27.(4分)(2022 烟台)如图,某海域中有A,B,C三个小岛,其中A在B的南偏西40°方向,C在B的南偏东35°方向,且B,C到A的距离相等,则小岛C相对于小岛A的方向是( )
A.北偏东70° B.北偏东75° C.南偏西70° D.南偏西20°
【解析】解:如图:
由题意得:
∠ABC=∠ABE+∠CBE=40°+35°=75°,AD∥BE,AB=AC,
∴∠ABC=∠C=75°,
∴∠BAC=180°﹣∠ABC﹣∠C=30°,
∵AD∥BE,
∴∠DAB=∠ABE=40°,
∴∠DAC=∠DAB+∠BAC=40°+30°=70°,
∴小岛C相对于小岛A的方向是北偏东70°,
故选:A.
28.(4分)(2022 甘肃)若∠A=40°,则∠A的余角的大小是( )
A.50° B.60° C.140° D.160°
【解析】解:∵∠A=40°,
∴∠A的余角为:90°﹣40°=50°,
故选:A.
29.(4分)(2021 百色)已知∠α=25°30′,则它的余角为( )
A.25°30′ B.64°30′ C.74°30′ D.154°30′
【解析】解:由题意得:∠α=25°30′,
故其余角为(90°﹣∠α)=64°30′.
故选:B.
30.(4分)(2022 台湾)缓降机是火灾发生时避难的逃生设备,如图是厂商提供的缓降机安装示意图,图中呈现在三楼安装缓降机时,使用此缓降机直接缓降到一楼地面的所需绳长(不计安全带).若某栋建筑的每个楼层高度皆为3公尺,则根据如图的安装方式在该建筑八楼安装缓降机时,使用此缓降机直接缓降到一楼地面的所需绳长(不计安全带)为多少公尺?( )
A.21.7 B.22.6 C.24.7 D.25.6
【解析】解:该建筑八楼安装缓降机时,使用此缓降机直接缓降到一楼地面的所需绳长=3×7+(1.6﹣0.4﹣0.5)=21.7(公尺),
故选:A.
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
【真题汇编】2023年中考数学备考之图形认识初步
1.认识立体图形
(1)几何图形:从实物中抽象出的各种图形叫几何图形.几何图形分为立体图形和平面图形.
(2)立体图形:有些几何图形(如长方体、正方体、圆柱、圆锥、球等)的各部分不都在同一个平面内,这就是立体图形.
(3)重点和难点突破:
结合实物,认识常见的立体图形,如:长方体、正方体、圆柱、圆锥、球、棱柱、棱锥等.能区分立体图形与平面图形,立体图形占有一定空间,各部分不都在同一平面内.
2.几何体的展开图
(1)多数立体图形是由平面图形围成的.沿着棱剪开就得到平面图形,这样的平面图形就是相应立体图形的展开图.同一个立体图形按不同的方式展开,得到的平面展开图是不一样的,同时也可看出,立体图形的展开图是平面图形.
(2)常见几何体的侧面展开图:
①圆柱的侧面展开图是长方形.②圆锥的侧面展开图是扇形.③正方体的侧面展开图是长方形.④三棱柱的侧面展开图是长方形.
(3)立体图形的侧面展开图,体现了平面图形与立体图形的联系.立体图形问题可以转化为平面图形问题解决.
从实物出发,结合具体的问题,辨析几何体的展开图,通过结合立体图形与平面图形的转化,建立空间观念,是解决此类问题的关键.
3.展开图折叠成几何体
通过结合立体图形与平面图形的相互转化,去理解和掌握几何体的展开图,要注意多从实物出发,然后再从给定的图形中辨认它们能否折叠成给定的立体图形.
4.专题:正方体相对两个面上的文字
(1)对于此类问题一般方法是用纸按图的样子折叠后可以解决,或是在对展开图理解的基础上直接想象.
(2)从实物出发,结合具体的问题,辨析几何体的展开图,通过结合立体图形与平面图形的转化,建立空间观念,是解决此类问题的关键.
(3)正方体的展开图有11种情况,分析平面展开图的各种情况后再认真确定哪两个面的对面.
5.截一个几何体
(1)截面:用一个平面去截一个几何体,截出的面叫做截面.
(2)截面的形状随截法的不同而改变,一般为多边形或圆,也可能是不规则图形,一般的截面与几何体的几个面相交就得到几条交线,截面就是几边形,因此,若一个几何体有几个面,则截面最多为几边形.
6.线段的性质:两点之间线段最短
线段公理
两点的所有连线中,可以有无数种连法,如折线、曲线、线段等,这些所有的线中,线段最短.
简单说成:两点之间,线段最短.
7.方向角
方向角是从正北或正南方向到目标方向所形成的小于90°的角
(1)方向角是表示方向的角;以正北,正南方向为基准,来描述物体所处的方向.
(2)用方向角描述方向时,通常以正北或正南方向为角的始边,以对象所处的射线为终边,故描述方向角时,一般先叙述北或南,再叙述偏东或偏西.(注意几个方向的角平分线按日常习惯,即东北,东南,西北,西南.)
(3)画方向角
以正南或正北方向作方向角的始边,另一边则表示对象所处的方向的射线.
8.度分秒的换算
(1)度、分、秒是常用的角的度量单位.1度=60分,即1°=60′,1分=60秒,即1′=60″.
(2)具体换算可类比时钟上的时、分、秒来说明角的度量单位度、分、秒之间也是60进制,将高级单位化为低级单位时,乘以60,反之,将低级单位转化为高级单位时除以60.同时,在进行度、分、秒的运算时也应注意借位和进位的方法.
9.余角和补角
(1)余角:如果两个角的和等于90°(直角),就说这两个角互为余角.即其中一个角是另一个角的余角.
(2)补角:如果两个角的和等于180°(平角),就说这两个角互为补角.即其中一个角是另一个角的补角.
(3)性质:等角的补角相等.等角的余角相等.
(4)余角和补角计算的应用,常常与等式的性质、等量代换相关联.
注意:余角(补角)与这两个角的位置没有关系.不论这两个角在哪儿,只要度数之和满足了定义,则它们就具备相应的关系.
【真题汇编】2023年中考数学备考之图形认识初步
(选择题30题)
满分:120分 建议时间:100分钟
学校:___________姓名:___________班级:___________考号:___________
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息2.请将答案正确填写在答题卡上
一.选择题(共30小题,满分120分,每小题4分)
1.(4分)(2022 北京)下面几何体中,是圆锥的为( )
A. B.
C. D.
2.(4分)(2022 自贡)如图,将矩形纸片ABCD绕边CD所在直线旋转一周,得到的立体图形是( )
A. B.
C. D.
3.(4分)(2022 河北)①~④是由相同的小正方体粘在一起的几何体,若组合其中的两个,恰是由6个小正方体构成的长方体,则应选择( )
A.①③ B.②③ C.③④ D.①④
4.(4分)(2022 柳州)如图,将矩形绕着它的一边所在的直线l旋转一周,可以得到的立体图形是( )
A. B. C. D.
5.(4分)(2022 泰州)如图为一个几何体的表面展开图,则该几何体是( )
A.三棱锥 B.四棱锥 C.四棱柱 D.圆锥
6.(4分)(2022 新疆)如图是某几何体的展开图,该几何体是( )
A.长方体 B.正方体 C.圆锥 D.圆柱
7.(4分)(2022 盐城)正方体的每个面上都有一个汉字,如图是它的一种平面展开图,那么在原正方体中,与“盐”字所在面相对的面上的汉字是( )
A.强 B.富 C.美 D.高
8.(4分)(2022 广州)如图是一个几何体的侧面展开图,这个几何体可以是( )
A.圆锥 B.圆柱 C.棱锥 D.棱柱
9.(4分)(2022 临沂)如图所示的三棱柱的展开图不可能是( )
A. B.
C. D.
10.(4分)(2022 广元)如图是某几何体的展开图,该几何体是( )
A.长方体 B.圆柱 C.圆锥 D.三棱柱
11.(4分)(2021 巴中)某立体图形的表面展开图如图所示,这个立体图形是( )
A. B. C. D.
12.(4分)(2022 常州)下列图形中,为圆柱的侧面展开图的是( )
A. B.
C. D.
13.(4分)(2022 绥化)下列图形中,正方体展开图错误的是( )
A. B.
C. D.
14.(4分)(2022 岳阳)某个立体图形的侧面展开图如图所示,它的底面是正三角形,那么这个立体图形是( )
A.圆柱 B.圆锥 C.三棱柱 D.四棱柱
15.(4分)(2022 宿迁)下列展开图中,是正方体展开图的是( )
A. B.
C. D.
16.(4分)(2022 台湾)如图为一个长方体的展开图,且长方体的底面为正方形.根据图中标示的长度,求此长方体的体积为何?( )
A.144 B.224 C.264 D.300
17.(4分)(2022 六盘水)如图,裁掉一个正方形后能折叠成正方体,但不能裁掉的是( )
A.① B.② C.③ D.④
18.(4分)(2022 遂宁)如图是正方体的一种展开图,那么在原正方体中与“我”字所在面相对的面上的汉字是( )
A.大 B.美 C.遂 D.宁
19.(4分)(2022 徐州)如图,已知骰子相对两面的点数之和为7,下列图形为该骰子表面展开图的是( )
A. B.
C. D.
20.(4分)(2022 资阳)如图是正方体的表面展开图,每个面内都分别写有一个字,则与“创”字相对面上的字是( )
A.文 B.明 C.城 D.市
21.(4分)(2022 内江)如图是正方体的表面展开图,则与“话”字相对的字是( )
A.跟 B.党 C.走 D.听
22.(4分)(2022 枣庄)某正方体的每个面上都有一个汉字,如图是它的一种展开图,那么在原正方体中,与“亮”字所在面相对的面上的汉字是( )
A.青 B.春 C.梦 D.想
23.(4分)(2021 黔西南州)如图是一个正方体的展开图,把它折叠成正方体后,有“学”字一面的相对面上的字是( )
A.雷 B.锋 C.精 D.神
24.(4分)(2022 淄博)经过折叠可以围成正方体,且在正方体侧面上的字恰好环绕组成一个四字成语的图形是( )
A. B.
C. D.
25.(4分)(2022 贵阳)如图,用一个平行于圆锥底面的平面截圆锥,截面的形状是( )
A. B.
C. D.
26.(4分)(2022 柳州)如图,从学校A到书店B有①、②、③、④四条路线,其中最短的路线是( )
A.① B.② C.③ D.④
27.(4分)(2022 烟台)如图,某海域中有A,B,C三个小岛,其中A在B的南偏西40°方向,C在B的南偏东35°方向,且B,C到A的距离相等,则小岛C相对于小岛A的方向是( )
A.北偏东70° B.北偏东75° C.南偏西70° D.南偏西20°
28.(4分)(2022 甘肃)若∠A=40°,则∠A的余角的大小是( )
A.50° B.60° C.140° D.160°
29.(4分)(2021 百色)已知∠α=25°30′,则它的余角为( )
A.25°30′ B.64°30′ C.74°30′ D.154°30′
30.(4分)(2022 台湾)缓降机是火灾发生时避难的逃生设备,如图是厂商提供的缓降机安装示意图,图中呈现在三楼安装缓降机时,使用此缓降机直接缓降到一楼地面的所需绳长(不计安全带).若某栋建筑的每个楼层高度皆为3公尺,则根据如图的安装方式在该建筑八楼安装缓降机时,使用此缓降机直接缓降到一楼地面的所需绳长(不计安全带)为多少公尺?( )
A.21.7 B.22.6 C.24.7 D.25.6
【真题汇编】2023年中考数学备考之图形认识初步(选择题30题)
参考答案与试题解析
一.选择题(共30小题,满分120分,每小题4分)
1.(4分)(2022 北京)下面几何体中,是圆锥的为( )
A. B.
C. D.
【解析】解:A是圆柱;
B是圆锥;
C是三棱锥,也叫四面体;
D是球体,简称球;
故选:B.
2.(4分)(2022 自贡)如图,将矩形纸片ABCD绕边CD所在直线旋转一周,得到的立体图形是( )
A. B.
C. D.
【解析】解:根据“点动成线,线动成面,面动成体”,
将矩形纸片ABCD绕边CD所在直线旋转一周,所得到的立体图形是圆柱.
故选:A.
3.(4分)(2022 河北)①~④是由相同的小正方体粘在一起的几何体,若组合其中的两个,恰是由6个小正方体构成的长方体,则应选择( )
A.①③ B.②③ C.③④ D.①④
【解析】解:由题意知,组合后的几何体是长方体且由6个小正方体构成,
∴①④符合要求,
故选:D.
4.(4分)(2022 柳州)如图,将矩形绕着它的一边所在的直线l旋转一周,可以得到的立体图形是( )
A. B. C. D.
【解析】解:将矩形绕着它的一边所在的直线l旋转一周,可以得到圆柱体,
故选:B.
5.(4分)(2022 泰州)如图为一个几何体的表面展开图,则该几何体是( )
A.三棱锥 B.四棱锥 C.四棱柱 D.圆锥
【解析】解:根据展开图可以得出是四棱锥的展开图,
故选:B.
6.(4分)(2022 新疆)如图是某几何体的展开图,该几何体是( )
A.长方体 B.正方体 C.圆锥 D.圆柱
【解析】解:根据展开图得该几何体是圆锥,
故选:C.
7.(4分)(2022 盐城)正方体的每个面上都有一个汉字,如图是它的一种平面展开图,那么在原正方体中,与“盐”字所在面相对的面上的汉字是( )
A.强 B.富 C.美 D.高
【解析】解:正方体的表面展开图相对的面之间一定相隔一个正方形,
“盐”与“高”是相对面,
“城”与“富”是相对面,
“强”与“美”是相对面,
故选:D.
8.(4分)(2022 广州)如图是一个几何体的侧面展开图,这个几何体可以是( )
A.圆锥 B.圆柱 C.棱锥 D.棱柱
【解析】解:∵圆锥的侧面展开图是扇形,
∴判断这个几何体是圆锥,
故选:A.
9.(4分)(2022 临沂)如图所示的三棱柱的展开图不可能是( )
A. B.
C. D.
【解析】解:如图所示的三棱柱的展开图不可能是;
故选:D.
10.(4分)(2022 广元)如图是某几何体的展开图,该几何体是( )
A.长方体 B.圆柱 C.圆锥 D.三棱柱
【解析】解:由两个圆和一个长方形可以围成圆柱,
故选:B.
11.(4分)(2021 巴中)某立体图形的表面展开图如图所示,这个立体图形是( )
A. B. C. D.
【解析】解:四个三角形和一个四边形,是四棱锥的组成,所以该立体图形的名称为四棱锥.
故选:A.
12.(4分)(2022 常州)下列图形中,为圆柱的侧面展开图的是( )
A. B.
C. D.
【解析】解:根据题意,把圆柱的侧面沿它的一条母线剪开展在一个平面上,
得到其侧面展开图是对边平行且相等的四边形;
又有母线垂直于上下底面,故可得是长方形.
故选:D.
13.(4分)(2022 绥化)下列图形中,正方体展开图错误的是( )
A. B.
C. D.
【解析】解:由展开图的知识可知,四个小正方形绝对不可能展开成田字形,故D选项都不符合题意.
故选:D.
14.(4分)(2022 岳阳)某个立体图形的侧面展开图如图所示,它的底面是正三角形,那么这个立体图形是( )
A.圆柱 B.圆锥 C.三棱柱 D.四棱柱
【解析】解:A选项,圆柱的底面是圆,故该选项不符合题意;
B选项,圆锥的底面是圆,故该选项不符合题意;
C选项,三棱柱的底面是三角形,侧面是三个长方形,故该选项符合题意;
D选项,四棱柱的底面是四边形,故该选项不符合题意;
故选:C.
15.(4分)(2022 宿迁)下列展开图中,是正方体展开图的是( )
A. B.
C. D.
【解析】解:由展开图的知识可知,四个小正方形绝对不可能展开成田字形,故A选项和D选项都不符合题意;
四个连成一排的小正方形可以围成前后左右四面,剩下的两面必须分在上下两面才能围成正方体,
故B选项不符合题意,C选项符合题意,
故选:C.
16.(4分)(2022 台湾)如图为一个长方体的展开图,且长方体的底面为正方形.根据图中标示的长度,求此长方体的体积为何?( )
A.144 B.224 C.264 D.300
【解析】解:设展开图的长方形的长为a,宽为b,
12=3b,2b+a=22,
解得a=14,b=4,
∴长方体的体积为:4×4×14=224,
故选:B.
17.(4分)(2022 六盘水)如图,裁掉一个正方形后能折叠成正方体,但不能裁掉的是( )
A.① B.② C.③ D.④
【解析】解:如图,裁掉一个正方形后能折叠成正方体,但不能裁掉的是①,
故选:A.
18.(4分)(2022 遂宁)如图是正方体的一种展开图,那么在原正方体中与“我”字所在面相对的面上的汉字是( )
A.大 B.美 C.遂 D.宁
【解析】解:由图可知,
我和美相对,爱和宁相对,大和遂相对,
故选:B.
19.(4分)(2022 徐州)如图,已知骰子相对两面的点数之和为7,下列图形为该骰子表面展开图的是( )
A. B.
C. D.
【解析】解:根据正方体的表面展开图,相对的面之间一定相隔一个正方形,
A、1点6点是相对面,3点与5点是相对面,2点与4点是相对面,所以不可以折成符合规则的骰子,故本选项不符合题意;
B、4点与3点是相对面,2点与6点是相对面,1点与5点是相对面,所以不可以折成符合规则的骰子,故本选项不符合题意;
C、3点与4点是相对面,2点与6点是相对面,1点与5点是相对面,所以不可以折成符合规则的骰子,故本选项不符合题意;
D、2点与5点是相对面,3点与4点是相对面,1点与6点是相对面,所以可以折成符合规则的骰子,故本选项符合题意.
故选:D.
20.(4分)(2022 资阳)如图是正方体的表面展开图,每个面内都分别写有一个字,则与“创”字相对面上的字是( )
A.文 B.明 C.城 D.市
【解析】解:将正方体的表面展开图还原成正方体,以“文”字为底,则左边的是“建”字,右边的是“明”字,上面的是“城”字,正面的是“市”字,后面的是“创”字,可知“创”字与“市”字相对.
故选:D.
21.(4分)(2022 内江)如图是正方体的表面展开图,则与“话”字相对的字是( )
A.跟 B.党 C.走 D.听
【解析】解:由正方体表面展开图的“相间、Z端是对面”可知,
“话”与“走”是对面,
故答案为:C.
22.(4分)(2022 枣庄)某正方体的每个面上都有一个汉字,如图是它的一种展开图,那么在原正方体中,与“亮”字所在面相对的面上的汉字是( )
A.青 B.春 C.梦 D.想
【解析】解:在原正方体中,与“亮”字所在面相对的面上的汉字是:想,
故选:D.
23.(4分)(2021 黔西南州)如图是一个正方体的展开图,把它折叠成正方体后,有“学”字一面的相对面上的字是( )
A.雷 B.锋 C.精 D.神
【解析】解:“学”与“神”是相对面,
“习”与“锋”是相对面,
“雷”与“精”是相对面.
故选:D.
24.(4分)(2022 淄博)经过折叠可以围成正方体,且在正方体侧面上的字恰好环绕组成一个四字成语的图形是( )
A. B.
C. D.
【解析】解:A、因为图中两个空白面不是相对面,所以图中的四个字不能恰好环绕组成一个四字成语,故A不符合题意;
B、因为图中两个空白面不是相对面,所以图中的四个字不能恰好环绕组成一个四字成语,故B不符合题意;
C、因为金与题是相对面,榜与名是相对面,所以正方体侧面上的字恰好环绕组成一个四字成语金榜题名,故C符合题意;
D、因为图中两个空白面不是相对面,所以图中的四个字不能恰好环绕组成一个四字成语,故D不符合题意;
故选:C.
25.(4分)(2022 贵阳)如图,用一个平行于圆锥底面的平面截圆锥,截面的形状是( )
A. B.
C. D.
【解析】解:用一个平行于圆锥底面的平面截圆锥,截面的形状是圆,
故选:B.
26.(4分)(2022 柳州)如图,从学校A到书店B有①、②、③、④四条路线,其中最短的路线是( )
A.① B.② C.③ D.④
【解析】解:根据题意可得,
从学校A到书店B有①、②、③、④四条路线,其中最短的路线是②.
故选:B.
27.(4分)(2022 烟台)如图,某海域中有A,B,C三个小岛,其中A在B的南偏西40°方向,C在B的南偏东35°方向,且B,C到A的距离相等,则小岛C相对于小岛A的方向是( )
A.北偏东70° B.北偏东75° C.南偏西70° D.南偏西20°
【解析】解:如图:
由题意得:
∠ABC=∠ABE+∠CBE=40°+35°=75°,AD∥BE,AB=AC,
∴∠ABC=∠C=75°,
∴∠BAC=180°﹣∠ABC﹣∠C=30°,
∵AD∥BE,
∴∠DAB=∠ABE=40°,
∴∠DAC=∠DAB+∠BAC=40°+30°=70°,
∴小岛C相对于小岛A的方向是北偏东70°,
故选:A.
28.(4分)(2022 甘肃)若∠A=40°,则∠A的余角的大小是( )
A.50° B.60° C.140° D.160°
【解析】解:∵∠A=40°,
∴∠A的余角为:90°﹣40°=50°,
故选:A.
29.(4分)(2021 百色)已知∠α=25°30′,则它的余角为( )
A.25°30′ B.64°30′ C.74°30′ D.154°30′
【解析】解:由题意得:∠α=25°30′,
故其余角为(90°﹣∠α)=64°30′.
故选:B.
30.(4分)(2022 台湾)缓降机是火灾发生时避难的逃生设备,如图是厂商提供的缓降机安装示意图,图中呈现在三楼安装缓降机时,使用此缓降机直接缓降到一楼地面的所需绳长(不计安全带).若某栋建筑的每个楼层高度皆为3公尺,则根据如图的安装方式在该建筑八楼安装缓降机时,使用此缓降机直接缓降到一楼地面的所需绳长(不计安全带)为多少公尺?( )
A.21.7 B.22.6 C.24.7 D.25.6
【解析】解:该建筑八楼安装缓降机时,使用此缓降机直接缓降到一楼地面的所需绳长=3×7+(1.6﹣0.4﹣0.5)=21.7(公尺),
故选:A.
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
