专题13 相交线与平行线(选择题40题)(含解析)-【冲刺2023中考】真题冲刺专题(知识点+专题训练)
文档属性
| 名称 | 专题13 相交线与平行线(选择题40题)(含解析)-【冲刺2023中考】真题冲刺专题(知识点+专题训练) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-12 09:50:18 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
【真题汇编】2023年中考数学备考之相交线与平行线
1.相交线
(1)相交线的定义
两条直线交于一点,我们称这两条直线相交.相对的,我们称这两条直线为相交线.
(2)两条相交线在形成的角中有特殊的数量关系和位置关系的有对顶角和邻补角两类.
(3)在同一平面内,两条直线的位置关系有两种:平行和相交(重合除外).
2.对顶角、邻补角
(1)对顶角:有一个公共顶点,并且一个角的两边分别是另一个角的两边的反向延长线,具有这种位置关系的两个角,互为对顶角.
(2)邻补角:只有一条公共边,它们的另一边互为反向延长线,具有这种关系的两个角,互为邻补角.
(3)对顶角的性质:对顶角相等.
(4)邻补角的性质:邻补角互补,即和为180°.
(5)邻补角、对顶角成对出现,在相交直线中,一个角的邻补角有两个.邻补角、对顶角都是相对与两个角而言,是指的两个角的一种位置关系.它们都是在两直线相交的前提下形成的.
3.垂线
(1)垂线的定义
当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线,它们的交点叫做垂足.
(2)垂线的性质
在平面内,过一点有且只有一条直线与已知直线垂直.
注意:“有且只有”中,“有”指“存在”,“只有”指“唯一”
“过一点”的点在直线上或直线外都可以.
4.垂线段最短
(1)垂线段:从直线外一点引一条直线的垂线,这点和垂足之间的线段叫做垂线段.
(2)垂线段的性质:垂线段最短.
正确理解此性质,垂线段最短,指的是从直线外一点到这条直线所作的垂线段最短.它是相对于这点与直线上其他各点的连线而言.
(3)实际问题中涉及线路最短问题时,其理论依据应从“两点之间,线段最短”和“垂线段最短”这两个中去选择.
5.同位角、内错角、同旁内角
(1)同位角:两条直线被第三条直线所截形成的角中,若两个角都在两直线的同侧,并且在第三条直线(截线)的同旁,则这样一对角叫做同位角.
(2)内错角:两条直线被第三条直线所截形成的角中,若两个角都在两直线的之间,并且在第三条直线(截线)的两旁,则这样一对角叫做内错角.
(3)同旁内角:两条直线被第三条直线所截形成的角中,若两个角都在两直线的之间,并且在第三条直线(截线)的同旁,则这样一对角叫做同旁内角.
(4)三线八角中的某两个角是不是同位角、内错角或同旁内角,完全由那两个角在图形中的相对位置决定.在复杂的图形中判别三类角时,应从角的两边入手,具有上述关系的角必有两边在同一直线上,此直线即为截线,而另外不在同一直线上的两边,它们所在的直线即为被截的线.同位角的边构成“F“形,内错角的边构成“Z“形,同旁内角的边构成“U”形.
6.平行公理及推论
(1)平行公理:经过直线外一点,有且只有一条直线与这条直线平行.
(2)平行公理中要准确理解“有且只有”的含义.从作图的角度说,它是“能但只能画出一条”的意思.
(3)推论:如果两条直线都与第三条直线平行,那么这两条直线也互相平行.
(4)平行公理的推论可以看做是平行线的一种判定方法,在解题中要注意该结论在证明直线平行时应用.
7.平行线的判定
(1)定理1:两条直线被第三条所截,如果同位角相等,那么这两条直线平行. 简单说成:同位角相等,两直线平行.
(2)定理2:两条直线被第三条所截,如果内错角相等,那么这两条直线平行.简单说成:内错角相等,两直线平行.
(3)定理3:两条直线被第三条所截,如果同旁内角互补,那么这两条直线平行.简单说成:同旁内角互补,两直线平行.
(4)定理4:两条直线都和第三条直线平行,那么这两条直线平行.
(5)定理5:在同一平面内,如果两条直线同时垂直于同一条直线,那么这两条直线平行.
8.平行线的性质
1、平行线性质定理
定理1:两条平行线被第三条直线所截,同位角相等. 简单说成:两直线平行,同位角相等.
定理2:两条平行线被地三条直线所截,同旁内角互补..简单说成:两直线平行,同旁内角互补.
定理3:两条平行线被第三条直线所截,内错角相等. 简单说成:两直线平行,内错角相等.
2、两条平行线之间的距离处处相等.
9.平行线的判定与性质
(1)平行线的判定是由角的数量关系判断两直线的位置关系.平行线的性质是由平行关系来寻找角的数量关系.
(2)应用平行线的判定和性质定理时,一定要弄清题设和结论,切莫混淆.
(3)平行线的判定与性质的联系与区别
区别:性质由形到数,用于推导角的关系并计算;判定由数到形,用于判定两直线平行.
联系:性质与判定的已知和结论正好相反,都是角的关系与平行线相关.
(4)辅助线规律,经常作出两平行线平行的直线或作出联系两直线的截线,构造出三类角.
【真题汇编】2023年中考数学备考之相交线与平行线
(选择题40题)
满分:120分 建议时间:100分钟
学校:___________姓名:___________班级:___________考号:___________
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息2.请将答案正确填写在答题卡上
一.选择题(共40小题,满分120分,每小题3分)
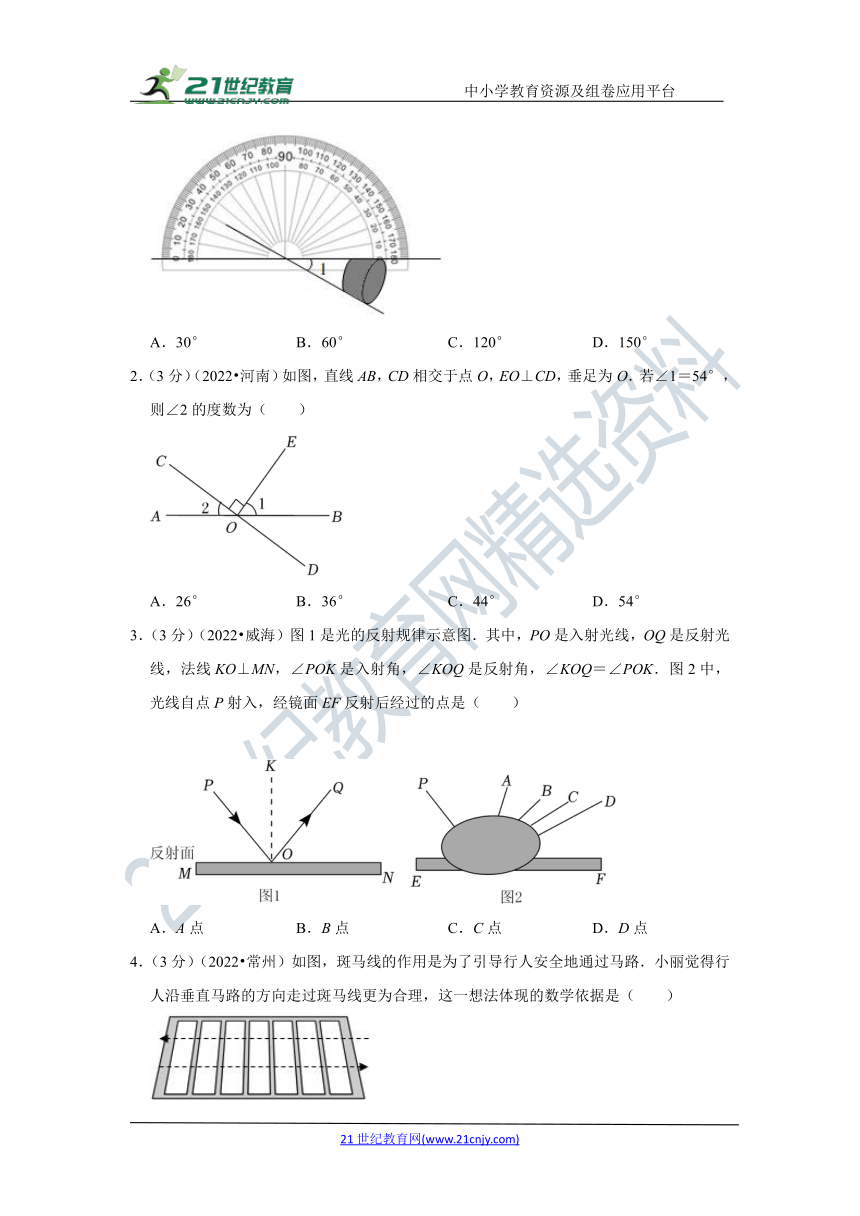
1.(3分)(2022 北京)如图,利用工具测量角,则∠1的大小为( )
A.30° B.60° C.120° D.150°
2.(3分)(2022 河南)如图,直线AB,CD相交于点O,EO⊥CD,垂足为O.若∠1=54°,则∠2的度数为( )
A.26° B.36° C.44° D.54°
3.(3分)(2022 威海)图1是光的反射规律示意图.其中,PO是入射光线,OQ是反射光线,法线KO⊥MN,∠POK是入射角,∠KOQ是反射角,∠KOQ=∠POK.图2中,光线自点P射入,经镜面EF反射后经过的点是( )
A.A点 B.B点 C.C点 D.D点
4.(3分)(2022 常州)如图,斑马线的作用是为了引导行人安全地通过马路.小丽觉得行人沿垂直马路的方向走过斑马线更为合理,这一想法体现的数学依据是( )
A.垂线段最短
B.两点确定一条直线
C.过一点有且只有一条直线与已知直线垂直
D.过直线外一点有且只有一条直线与已知直线平行
5.(3分)(2022 青海)数学课上老师用双手形象的表示了“三线八角”图形,如图所示(两大拇指代表被截直线,食指代表截线).从左至右依次表示( )
A.同旁内角、同位角、内错角
B.同位角、内错角、对顶角
C.对顶角、同位角、同旁内角
D.同位角、内错角、同旁内角
6.(3分)(2022 贺州)如图,直线a,b被直线c所截,下列各组角是同位角的是( )
A.∠1与∠2 B.∠1与∠3 C.∠2与∠3 D.∠3与∠4
7.(3分)(2022 吉林)如图,如果∠1=∠2,那么AB∥CD,其依据可以简单说成( )
A.两直线平行,内错角相等
B.内错角相等,两直线平行
C.两直线平行,同位角相等
D.同位角相等,两直线平行
8.(3分)(2022 台州)如图,已知∠1=90°,为保证两条铁轨平行,添加的下列条件中,正确的是( )
A.∠2=90° B.∠3=90° C.∠4=90° D.∠5=90°
9.(3分)(2022 资阳)将直尺和三角板按如图所示的位置放置.若∠1=40°,则∠2度数是( )
A.60° B.50° C.40° D.30°
10.(3分)(2022 河池)如图,平行线a,b被直线c所截,若∠1=142°,则∠2的度数是( )
A.142° B.132° C.58° D.38°
11.(3分)(2022 西藏)如图,l1∥l2,∠1=38°,∠2=46°,则∠3的度数为( )
A.46° B.90° C.96° D.134°
12.(3分)(2022 柳州)如图,直线a,b被直线c所截,若a∥b,∠1=70°,则∠2的度数是( )
A.50° B.60° C.70° D.110°
13.(3分)(2022 长沙)如图,AB∥CD,AE∥CF,∠BAE=75°,则∠DCF的度数为( )
A.65° B.70° C.75° D.105°
14.(3分)(2022 恩施州)已知直线l1∥l2,将含30°角的直角三角板按如图所示摆放.若∠1=120°,则∠2=( )
A.120° B.130° C.140° D.150°
15.(3分)(2022 湖北)如图,AB∥CD,直线EF分别交AB,CD于点E,F.∠BEF的平分线交CD于点G.若∠EFG=52°,则∠EGF=( )
A.128° B.64° C.52° D.26°
16.(3分)(2022 随州)如图,直线l1∥l2,直线l与l1,l2相交,若图中∠1=60°,则∠2为( )
A.30° B.40° C.50° D.60°
17.(3分)(2022 威海)如图,在方格纸中,点P,Q,M的坐标分别记为(0,2),(3,0),(1,4).若MN∥PQ,则点N的坐标可能是( )
A.(2,3) B.(3,3) C.(4,2) D.(5,1)
18.(3分)(2022 内蒙古)如图,直线a∥b,截线c,d相交成30°角,∠1=146°33′,则∠2的度数是( )
A.63°27′ B.64°27′ C.64°33′ D.63°33′
19.(3分)(2022 襄阳)已知直线m∥n,将一块含30°角的直角三角板ABC(∠ABC=30°,∠BAC=60°)按如图方式放置,点A,B分别落在直线m,n上.若∠1=70°.则∠2的度数为( )
A.30° B.40° C.60° D.70°
20.(3分)(2022 锦州)如图,直线a∥b,将含30°角的直角三角板ABC(∠ABC=30°)按图中位置摆放,若∠1=110°,则∠2的度数为( )
A.30° B.36° C.40° D.50°
21.(3分)(2022 南通)如图,a∥b,∠3=80°,∠1﹣∠2=20°,则∠1的度数是( )
A.30° B.40° C.50° D.80°
22.(3分)(2022 六盘水)如图,a∥b,∠1=43°,则∠2的度数是( )
A.137° B.53° C.47° D.43°
23.(3分)(2022 兰州)如图,直线a∥b,直线c与直线a,b分别相交于点A,B,AC⊥b,垂足为C.若∠1=52°,则∠2=( )
A.52° B.45° C.38° D.26°
24.(3分)(2022 大连)如图,平行线AB,CD被直线EF所截,FG平分∠EFD,若∠EFD=70°,则∠EGF的度数是( )
A.35° B.55° C.70° D.110°
25.(3分)(2022 盐城)小明将一块直角三角板摆放在直尺上,如图所示,则∠ABC与∠DEF的关系是( )
A.互余 B.互补 C.同位角 D.同旁内角
26.(3分)(2022 营口)如图,直线DE∥FG,Rt△ABC的顶点B,C分别在DE,FG上,若∠BCF=25°,则∠ABE的大小为( )
A.55° B.25° C.65° D.75°
27.(3分)(2022 娄底)一杆古秤在称物时的状态如图所示,已知∠1=80°,则∠2=( )
A.20° B.80° C.100° D.120°
28.(3分)(2022 桂林)如图,直线a,b被直线c所截,且a∥b,若∠1=60°,则∠2的度数是( )
A.70° B.60° C.50° D.40°
29.(3分)(2022 齐齐哈尔)如图所示,直线a∥b,点A在直线a上,点B在直线b上,AC=BC,∠C=120°,∠1=43°,则∠2的度数为( )
A.57° B.63° C.67° D.73°
30.(3分)(2022 山西)如图,Rt△ABC是一块直角三角板,其中∠C=90°,∠BAC=30°.直尺的一边DE经过顶点A,若DE∥CB,则∠DAB的度数为( )
A.100° B.120° C.135° D.150°
31.(3分)(2022 东营)如图,直线a∥b,一个三角板的直角顶点在直线a上,两直角边均与直线b相交,∠1=40°,则∠2=( )
A.40° B.50° C.60° D.65°
32.(3分)(2022 菏泽)如图所示,将一矩形纸片沿AB折叠,已知∠ABC=36°,则∠D1AD=( )
A.48° B.66° C.72° D.78°
33.(3分)(2022 济南)如图,AB∥CD,点E在AB上,EC平分∠AED,若∠1=65°,则∠2的度数为( )
A.45° B.50° C.57.5° D.65°
34.(3分)(2022 丹东)如图,直线l1∥l2,直线l3与l1,l2分别交于A,B两点,过点A作AC⊥l2,垂足为C,若∠1=52°,则∠2的度数是( )
A.32° B.38° C.48° D.52°
35.(3分)(2022 通辽)如图,一束光线AB先后经平面镜OM,ON反射后,反射光线CD与AB平行,当∠ABM=35°时,∠DCN的度数为( )
A.55° B.70° C.60° D.35°
36.(3分)(2022 潍坊)如图是小亮绘制的潜望镜原理示意图,两个平面镜的镜面AB与CD平行,入射光线l与出射光线m平行.若入射光线l与镜面AB的夹角∠1=40°10',则∠6的度数为( )
A.100°40' B.99°80' C.99°40' D.99°20'
37.(3分)(2022 辽宁)如图,直线m∥n,AC⊥BC于点C,∠1=30°,则∠2的度数为( )
A.140° B.130° C.120° D.110°
38.(3分)(2022 台湾)如图为两直线L、M与△ABC相交的情形,其中L、M分别与BC、AB平行.根据图中标示的角度,求∠B的度数为何?( )
A.55 B.60 C.65 D.70
39.(3分)(2022 深圳)一副三角板如图所示放置,斜边平行,则∠1的度数为( )
A.5° B.10° C.15° D.20°
40.(3分)(2022 郴州)如图,直线a∥b,且直线a,b被直线c,d所截,则下列条件不能判定直线c∥d的是( )
A.∠3=∠4 B.∠1+∠5=180° C.∠1=∠2 D.∠1=∠4
【真题汇编】2023年中考数学备考之相交线与平行线(选择题40题)
参考答案与试题解析
一.选择题(共40小题,满分120分,每小题3分)
1.(3分)(2022 北京)如图,利用工具测量角,则∠1的大小为( )
A.30° B.60° C.120° D.150°
【解析】解:根据对顶角相等的性质,可得:∠1=30°,
故选:A.
2.(3分)(2022 河南)如图,直线AB,CD相交于点O,EO⊥CD,垂足为O.若∠1=54°,则∠2的度数为( )
A.26° B.36° C.44° D.54°
【解析】解:∵EO⊥CD,
∴∠COE=90°,
∵∠1+∠COE+∠2=180°,
∴∠2=180°﹣∠1﹣∠COE=180°﹣54°﹣90°=36°.
故选:B.
3.(3分)(2022 威海)图1是光的反射规律示意图.其中,PO是入射光线,OQ是反射光线,法线KO⊥MN,∠POK是入射角,∠KOQ是反射角,∠KOQ=∠POK.图2中,光线自点P射入,经镜面EF反射后经过的点是( )
A.A点 B.B点 C.C点 D.D点
【解析】解:根据直线的性质补全图2并作出法线OK,如下图所示:
根据图形可以看出OB是反射光线,
故选:B.
4.(3分)(2022 常州)如图,斑马线的作用是为了引导行人安全地通过马路.小丽觉得行人沿垂直马路的方向走过斑马线更为合理,这一想法体现的数学依据是( )
A.垂线段最短
B.两点确定一条直线
C.过一点有且只有一条直线与已知直线垂直
D.过直线外一点有且只有一条直线与已知直线平行
【解析】解:小丽觉得行人沿垂直马路的方向走过斑马线更为合理,这一想法体现的数学依据是垂线段最短,
故选:A.
5.(3分)(2022 青海)数学课上老师用双手形象的表示了“三线八角”图形,如图所示(两大拇指代表被截直线,食指代表截线).从左至右依次表示( )
A.同旁内角、同位角、内错角
B.同位角、内错角、对顶角
C.对顶角、同位角、同旁内角
D.同位角、内错角、同旁内角
【解析】解:根据同位角、内错角、同旁内角的概念,可知
第一个图是同位角,第二个图是内错角,第三个图是同旁内角.
故选:D.
6.(3分)(2022 贺州)如图,直线a,b被直线c所截,下列各组角是同位角的是( )
A.∠1与∠2 B.∠1与∠3 C.∠2与∠3 D.∠3与∠4
【解析】解:根据同位角、邻补角、对顶角的定义进行判断,
A、∠1和∠2是对顶角,故A错误;
B、∠1和∠3是同位角,故B正确;
C、∠2和∠3是内错角,故C错误;
D、∠3和∠4是邻补角,故D错误.
故选:B.
7.(3分)(2022 吉林)如图,如果∠1=∠2,那么AB∥CD,其依据可以简单说成( )
A.两直线平行,内错角相等
B.内错角相等,两直线平行
C.两直线平行,同位角相等
D.同位角相等,两直线平行
【解析】解:∵∠1=∠2,
∴AB∥CD(同位角相等,两直线平行),
故选:D.
8.(3分)(2022 台州)如图,已知∠1=90°,为保证两条铁轨平行,添加的下列条件中,正确的是( )
A.∠2=90° B.∠3=90° C.∠4=90° D.∠5=90°
【解析】解:A.由∠2=90°不能判定两条铁轨平行,故该选项不符合题意;
B.由∠3=90°=∠1,可判定两枕木平行,故该选项不符合题意;
C.∵∠1=90°,∠4=90°,
∴∠1=∠4,
∴两条铁轨平行,故该选项符合题意;
D.由∠5=90°不能判定两条铁轨平行,故该选项不符合题意;
故选:C.
9.(3分)(2022 资阳)将直尺和三角板按如图所示的位置放置.若∠1=40°,则∠2度数是( )
A.60° B.50° C.40° D.30°
【解析】解:如图,根据题意可知∠A为直角,直尺的两条边平行,
∴∠2=∠ACB,
∵∠ACB+∠ABC=90°,∠ABC=∠1,
∴∠2=90°﹣∠1=90°﹣40°=50°,
故选:B.
10.(3分)(2022 河池)如图,平行线a,b被直线c所截,若∠1=142°,则∠2的度数是( )
A.142° B.132° C.58° D.38°
【解析】解:∵a∥b,
∴∠2=∠1=142°.
故选:A.
11.(3分)(2022 西藏)如图,l1∥l2,∠1=38°,∠2=46°,则∠3的度数为( )
A.46° B.90° C.96° D.134°
【解析】解:∵l1∥l2,
∴∠1+∠3+∠2=180°,
∵∠1=38°,∠2=46°,
∴∠3=96°,
故选:C.
12.(3分)(2022 柳州)如图,直线a,b被直线c所截,若a∥b,∠1=70°,则∠2的度数是( )
A.50° B.60° C.70° D.110°
【解析】解:∵a∥b,
∴∠2=∠1=70°.
故选:C.
13.(3分)(2022 长沙)如图,AB∥CD,AE∥CF,∠BAE=75°,则∠DCF的度数为( )
A.65° B.70° C.75° D.105°
【解析】解:如图:
∵AB∥CD,
∴∠DGE=∠BAE=75°,
∵AE∥CF,
∴∠DCF=∠DGE=75°,
故选:C.
14.(3分)(2022 恩施州)已知直线l1∥l2,将含30°角的直角三角板按如图所示摆放.若∠1=120°,则∠2=( )
A.120° B.130° C.140° D.150°
【解析】解:过含30°角的直角三角板的直角顶点B作BF∥l1,交AC于点F,
∵∠C=30°,
∴∠A=90°﹣∠C=60°.
∵∠1=∠A+∠ADE,
∴∠ADE=60°.
∵BF∥l1,
∴∠ABF=∠ADE=60°,
∴∠FBG=90°﹣∠ABF=30°.
∵BF∥l1,l1∥l2,
∴BF∥l2,
∴∠BGH+∠FBG=180°,
∴∠BGH=180°﹣∠FBG=150°,
∴∠2=∠BGH=150°.
故选:D.
15.(3分)(2022 湖北)如图,AB∥CD,直线EF分别交AB,CD于点E,F.∠BEF的平分线交CD于点G.若∠EFG=52°,则∠EGF=( )
A.128° B.64° C.52° D.26°
【解析】解:∵AB∥CD,
∴∠FEB=180°﹣∠EFG=128°,
∵EG平分∠BEF,
∴∠BEG=∠BEF=64°,
∵AB∥CD,
∴∠EGF=∠BEG=64°.
故答案选:B.
16.(3分)(2022 随州)如图,直线l1∥l2,直线l与l1,l2相交,若图中∠1=60°,则∠2为( )
A.30° B.40° C.50° D.60°
【解析】解:∵l1∥l2,
∴∠1=∠2,
∵∠1=60°,
∴∠2=60°,
故选:D.
17.(3分)(2022 威海)如图,在方格纸中,点P,Q,M的坐标分别记为(0,2),(3,0),(1,4).若MN∥PQ,则点N的坐标可能是( )
A.(2,3) B.(3,3) C.(4,2) D.(5,1)
【解析】解:如图所示,
∵P(0,2),Q(3,0)M(1,4),
MN∥PQ,
∴N(4,2).
故选:C.
18.(3分)(2022 内蒙古)如图,直线a∥b,截线c,d相交成30°角,∠1=146°33′,则∠2的度数是( )
A.63°27′ B.64°27′ C.64°33′ D.63°33′
27',利用三角形的外角性质即可求∠2.
【解析】解:如图,
∵∠1=146°33′,
∴∠3=180°﹣∠1=33°27',
∵a∥b,
∴∠4=∠3=33°27',
∵∠A=30°,∠2=∠4+∠A,
∴∠2=33°27'+30°=63°27'.
故选:A.
19.(3分)(2022 襄阳)已知直线m∥n,将一块含30°角的直角三角板ABC(∠ABC=30°,∠BAC=60°)按如图方式放置,点A,B分别落在直线m,n上.若∠1=70°.则∠2的度数为( )
A.30° B.40° C.60° D.70°
【解析】解:∵m∥n,∠1=70°,
∴∠1=∠ABD=70°,
∵∠ABC=30°,
∴∠2=∠ABD﹣∠ABC=40°,
故选:B.
20.(3分)(2022 锦州)如图,直线a∥b,将含30°角的直角三角板ABC(∠ABC=30°)按图中位置摆放,若∠1=110°,则∠2的度数为( )
A.30° B.36° C.40° D.50°
【解析】解:如图,
∵a∥b,∠1=110°,
∴∠3=∠1=110°,
∴∠4=180°﹣∠3=70°,
∵∠B=30°
∴∠2=∠4﹣∠B=40°;
故选:C.
21.(3分)(2022 南通)如图,a∥b,∠3=80°,∠1﹣∠2=20°,则∠1的度数是( )
A.30° B.40° C.50° D.80°
【解析】解:如图:
∵a∥b,
∴∠1=∠4,
∵∠3是△ABC的一个外角,
∴∠3=∠4+∠2,
∵∠3=80°,
∴∠1+∠2=80°,
∵∠1﹣∠2=20°,
∴2∠1+∠2﹣∠2=100°,
∴∠1=50°,
故选:C.
22.(3分)(2022 六盘水)如图,a∥b,∠1=43°,则∠2的度数是( )
A.137° B.53° C.47° D.43°
【解析】解:∵a∥b,∠1=43°,
∴∠2=∠1=43°.
故选:D.
23.(3分)(2022 兰州)如图,直线a∥b,直线c与直线a,b分别相交于点A,B,AC⊥b,垂足为C.若∠1=52°,则∠2=( )
A.52° B.45° C.38° D.26°
【解析】解:∵a∥b,
∴∠1=∠ABC=52°,
∵AC⊥b,
∴∠ACB=90°,
∴∠2=90°﹣∠ABC=38°,
故选:C.
24.(3分)(2022 大连)如图,平行线AB,CD被直线EF所截,FG平分∠EFD,若∠EFD=70°,则∠EGF的度数是( )
A.35° B.55° C.70° D.110°
【解析】解:∵FG平分∠EFD,∠EFD=70°,
∴∠GFD=∠EFD=×70°=35°,
∵AB∥CD,
∴∠EGF=∠GFD=35°.
故选:A.
25.(3分)(2022 盐城)小明将一块直角三角板摆放在直尺上,如图所示,则∠ABC与∠DEF的关系是( )
A.互余 B.互补 C.同位角 D.同旁内角
【解析】解:如图,
过点G作GH∥ED,
∵BC∥ED,
∴ED∥GH∥BC,
∴∠ABC=∠AGH,∠DEF=∠HGF,
∵∠HGF+∠AGH=90°,
∴∠ABC+∠DEF=90°
∴∠DEF和∠ABC互余,
故选:A.
26.(3分)(2022 营口)如图,直线DE∥FG,Rt△ABC的顶点B,C分别在DE,FG上,若∠BCF=25°,则∠ABE的大小为( )
A.55° B.25° C.65° D.75°
【解析】解:∵DE∥FG,∠BCF=25°,
∴∠CBE=∠BCF=25°,
∵∠ABC=90°,
∴∠ABE=∠ABC﹣∠CBE=65°.
故选:C.
27.(3分)(2022 娄底)一杆古秤在称物时的状态如图所示,已知∠1=80°,则∠2=( )
A.20° B.80° C.100° D.120°
【解析】解:如图,
由平行线的性质得:∠3=∠1=80°,
∵∠2+∠3=180°,
∴∠2=180°﹣80°=100°.
故选:C.
28.(3分)(2022 桂林)如图,直线a,b被直线c所截,且a∥b,若∠1=60°,则∠2的度数是( )
A.70° B.60° C.50° D.40°
【解析】解:∵a∥b,
∴∠1=∠2,
∵∠1=60°,
∴∠2=60°,
故选:B.
29.(3分)(2022 齐齐哈尔)如图所示,直线a∥b,点A在直线a上,点B在直线b上,AC=BC,∠C=120°,∠1=43°,则∠2的度数为( )
A.57° B.63° C.67° D.73°
【解析】解:∵AC=BC,∠ACB=120°,
∴∠CBA=∠CAB=,
∵a∥b,
∴∠2=∠CBA+∠1=30°+43°=73°.
故选:D.
30.(3分)(2022 山西)如图,Rt△ABC是一块直角三角板,其中∠C=90°,∠BAC=30°.直尺的一边DE经过顶点A,若DE∥CB,则∠DAB的度数为( )
A.100° B.120° C.135° D.150°
【解析】解:∵DE∥CB,∠C=90°,
∴∠DAC=∠C=90°,
∵∠BAC=30°,
∴∠DAB=∠DAC+∠BAC=120°,
故答案为:B.
31.(3分)(2022 东营)如图,直线a∥b,一个三角板的直角顶点在直线a上,两直角边均与直线b相交,∠1=40°,则∠2=( )
A.40° B.50° C.60° D.65°
【解析】解:如图:
∵∠4=90°,∠1=40°,∠1+∠3+∠4=180°,
∴∠3=180°﹣90°﹣40°=50°,
∵直线a∥b,
∴∠2=∠3=50°.
故选:B.
32.(3分)(2022 菏泽)如图所示,将一矩形纸片沿AB折叠,已知∠ABC=36°,则∠D1AD=( )
A.48° B.66° C.72° D.78°
【解析】解:根据题意可得:∠BAD=∠BAD1,
∵矩形纸片的对边平行,即ED∥BC,
∴∠ABC+∠BAD=180°,
∵∠ABC=36°,
∴∠BAD=180°﹣36°=144°,
∴∠BAD1=∠BAD=144°,
∴∠D1AD=360°﹣∠BAD1﹣∠BAD=360°﹣144°﹣144°=72°.
故选:C.
33.(3分)(2022 济南)如图,AB∥CD,点E在AB上,EC平分∠AED,若∠1=65°,则∠2的度数为( )
A.45° B.50° C.57.5° D.65°
【解析】解:∵AB∥CD,
∴∠AEC=∠1=65°.
∵EC平分∠AED,
∴∠AED=2∠AEC=130°.
∴∠2=180°﹣∠AED=50°.
故选:B.
34.(3分)(2022 丹东)如图,直线l1∥l2,直线l3与l1,l2分别交于A,B两点,过点A作AC⊥l2,垂足为C,若∠1=52°,则∠2的度数是( )
A.32° B.38° C.48° D.52°
【解析】解:∵直线l1∥l2,∠1=52°,
∴∠ABC=∠1=52°,
∵AC⊥l2,
∴∠ACB=90°,
∴∠2=180°﹣∠ABC﹣∠ACB=180°﹣52°﹣90°=38°,
故选:B.
35.(3分)(2022 通辽)如图,一束光线AB先后经平面镜OM,ON反射后,反射光线CD与AB平行,当∠ABM=35°时,∠DCN的度数为( )
A.55° B.70° C.60° D.35°
【解析】解:∵∠ABM=35°,∠ABM=∠OBC,
∴∠OBC=35°,
∴∠ABC=180°﹣∠ABM﹣∠OBC=180°﹣35°﹣35°=110°,
∵CD∥AB,
∴∠ABC+∠BCD=180°,
∴∠BCD=180°﹣∠ABC=70°,
∵∠BCO=∠DCN,∠BCO+∠BCD+∠DCN=180°,
∴∠DCN=(180°﹣∠BCD)=55°,
故选:A.
36.(3分)(2022 潍坊)如图是小亮绘制的潜望镜原理示意图,两个平面镜的镜面AB与CD平行,入射光线l与出射光线m平行.若入射光线l与镜面AB的夹角∠1=40°10',则∠6的度数为( )
A.100°40' B.99°80' C.99°40' D.99°20'
【解析】解:∵入射角等于反射角,∠1=40°10',
∴∠2=∠1=40°10',
∵∠1+∠2+∠5=180°,
∴∠5=180°﹣40°10'﹣40°10'=99°40',
∵入射光线l与出射光线m平行,
∴∠6=∠5=99°40'.
故选:C.
37.(3分)(2022 辽宁)如图,直线m∥n,AC⊥BC于点C,∠1=30°,则∠2的度数为( )
A.140° B.130° C.120° D.110°
【解析】解:∵AC⊥BC于点C,
∴∠ACB=90°,
∴∠ABC+∠1=90°,
∴∠ABC=90°﹣30°=60°,
∵m∥n,
∴∠2=180°﹣∠ABC=120°.
故选:C.
38.(3分)(2022 台湾)如图为两直线L、M与△ABC相交的情形,其中L、M分别与BC、AB平行.根据图中标示的角度,求∠B的度数为何?( )
A.55 B.60 C.65 D.70
【解析】解:因为L、M分别与BC、AB平行,
所以∠C+120°=180°,∠A+115°=180°,
所以∠C=60°,∠A=65°,
所以∠B=180°﹣∠C=∠A=55°.
故选:A.
39.(3分)(2022 深圳)一副三角板如图所示放置,斜边平行,则∠1的度数为( )
A.5° B.10° C.15° D.20°
【解析】解:如图,∠ACB=45°,∠F=30°,
∵BC∥EF,
∴∠DCB=∠F=30°,
∴∠1=45°﹣30°=15°,
故选:C.
40.(3分)(2022 郴州)如图,直线a∥b,且直线a,b被直线c,d所截,则下列条件不能判定直线c∥d的是( )
A.∠3=∠4 B.∠1+∠5=180° C.∠1=∠2 D.∠1=∠4
【解析】解:A、若∠3=∠4时,由“内错角相等,两直线平行”可以判定c∥d,不符合题意;
B、若∠1+∠5=180°时,由“同旁内角互补,两直线平行”可以判定c∥d,不符合题意;
C、若∠1=∠2时,由“内错角相等,两直线平行”可以判定a∥b,不能判定c∥d,符合题意;
D、由a∥b推知∠4+∠5=180°.若∠1=∠4时,则∠1+∠5=180°,由“同旁内角互补,两直线平行”可以判定c∥d,不符合题意.
故选:C.
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
【真题汇编】2023年中考数学备考之相交线与平行线
1.相交线
(1)相交线的定义
两条直线交于一点,我们称这两条直线相交.相对的,我们称这两条直线为相交线.
(2)两条相交线在形成的角中有特殊的数量关系和位置关系的有对顶角和邻补角两类.
(3)在同一平面内,两条直线的位置关系有两种:平行和相交(重合除外).
2.对顶角、邻补角
(1)对顶角:有一个公共顶点,并且一个角的两边分别是另一个角的两边的反向延长线,具有这种位置关系的两个角,互为对顶角.
(2)邻补角:只有一条公共边,它们的另一边互为反向延长线,具有这种关系的两个角,互为邻补角.
(3)对顶角的性质:对顶角相等.
(4)邻补角的性质:邻补角互补,即和为180°.
(5)邻补角、对顶角成对出现,在相交直线中,一个角的邻补角有两个.邻补角、对顶角都是相对与两个角而言,是指的两个角的一种位置关系.它们都是在两直线相交的前提下形成的.
3.垂线
(1)垂线的定义
当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线,它们的交点叫做垂足.
(2)垂线的性质
在平面内,过一点有且只有一条直线与已知直线垂直.
注意:“有且只有”中,“有”指“存在”,“只有”指“唯一”
“过一点”的点在直线上或直线外都可以.
4.垂线段最短
(1)垂线段:从直线外一点引一条直线的垂线,这点和垂足之间的线段叫做垂线段.
(2)垂线段的性质:垂线段最短.
正确理解此性质,垂线段最短,指的是从直线外一点到这条直线所作的垂线段最短.它是相对于这点与直线上其他各点的连线而言.
(3)实际问题中涉及线路最短问题时,其理论依据应从“两点之间,线段最短”和“垂线段最短”这两个中去选择.
5.同位角、内错角、同旁内角
(1)同位角:两条直线被第三条直线所截形成的角中,若两个角都在两直线的同侧,并且在第三条直线(截线)的同旁,则这样一对角叫做同位角.
(2)内错角:两条直线被第三条直线所截形成的角中,若两个角都在两直线的之间,并且在第三条直线(截线)的两旁,则这样一对角叫做内错角.
(3)同旁内角:两条直线被第三条直线所截形成的角中,若两个角都在两直线的之间,并且在第三条直线(截线)的同旁,则这样一对角叫做同旁内角.
(4)三线八角中的某两个角是不是同位角、内错角或同旁内角,完全由那两个角在图形中的相对位置决定.在复杂的图形中判别三类角时,应从角的两边入手,具有上述关系的角必有两边在同一直线上,此直线即为截线,而另外不在同一直线上的两边,它们所在的直线即为被截的线.同位角的边构成“F“形,内错角的边构成“Z“形,同旁内角的边构成“U”形.
6.平行公理及推论
(1)平行公理:经过直线外一点,有且只有一条直线与这条直线平行.
(2)平行公理中要准确理解“有且只有”的含义.从作图的角度说,它是“能但只能画出一条”的意思.
(3)推论:如果两条直线都与第三条直线平行,那么这两条直线也互相平行.
(4)平行公理的推论可以看做是平行线的一种判定方法,在解题中要注意该结论在证明直线平行时应用.
7.平行线的判定
(1)定理1:两条直线被第三条所截,如果同位角相等,那么这两条直线平行. 简单说成:同位角相等,两直线平行.
(2)定理2:两条直线被第三条所截,如果内错角相等,那么这两条直线平行.简单说成:内错角相等,两直线平行.
(3)定理3:两条直线被第三条所截,如果同旁内角互补,那么这两条直线平行.简单说成:同旁内角互补,两直线平行.
(4)定理4:两条直线都和第三条直线平行,那么这两条直线平行.
(5)定理5:在同一平面内,如果两条直线同时垂直于同一条直线,那么这两条直线平行.
8.平行线的性质
1、平行线性质定理
定理1:两条平行线被第三条直线所截,同位角相等. 简单说成:两直线平行,同位角相等.
定理2:两条平行线被地三条直线所截,同旁内角互补..简单说成:两直线平行,同旁内角互补.
定理3:两条平行线被第三条直线所截,内错角相等. 简单说成:两直线平行,内错角相等.
2、两条平行线之间的距离处处相等.
9.平行线的判定与性质
(1)平行线的判定是由角的数量关系判断两直线的位置关系.平行线的性质是由平行关系来寻找角的数量关系.
(2)应用平行线的判定和性质定理时,一定要弄清题设和结论,切莫混淆.
(3)平行线的判定与性质的联系与区别
区别:性质由形到数,用于推导角的关系并计算;判定由数到形,用于判定两直线平行.
联系:性质与判定的已知和结论正好相反,都是角的关系与平行线相关.
(4)辅助线规律,经常作出两平行线平行的直线或作出联系两直线的截线,构造出三类角.
【真题汇编】2023年中考数学备考之相交线与平行线
(选择题40题)
满分:120分 建议时间:100分钟
学校:___________姓名:___________班级:___________考号:___________
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息2.请将答案正确填写在答题卡上
一.选择题(共40小题,满分120分,每小题3分)
1.(3分)(2022 北京)如图,利用工具测量角,则∠1的大小为( )
A.30° B.60° C.120° D.150°
2.(3分)(2022 河南)如图,直线AB,CD相交于点O,EO⊥CD,垂足为O.若∠1=54°,则∠2的度数为( )
A.26° B.36° C.44° D.54°
3.(3分)(2022 威海)图1是光的反射规律示意图.其中,PO是入射光线,OQ是反射光线,法线KO⊥MN,∠POK是入射角,∠KOQ是反射角,∠KOQ=∠POK.图2中,光线自点P射入,经镜面EF反射后经过的点是( )
A.A点 B.B点 C.C点 D.D点
4.(3分)(2022 常州)如图,斑马线的作用是为了引导行人安全地通过马路.小丽觉得行人沿垂直马路的方向走过斑马线更为合理,这一想法体现的数学依据是( )
A.垂线段最短
B.两点确定一条直线
C.过一点有且只有一条直线与已知直线垂直
D.过直线外一点有且只有一条直线与已知直线平行
5.(3分)(2022 青海)数学课上老师用双手形象的表示了“三线八角”图形,如图所示(两大拇指代表被截直线,食指代表截线).从左至右依次表示( )
A.同旁内角、同位角、内错角
B.同位角、内错角、对顶角
C.对顶角、同位角、同旁内角
D.同位角、内错角、同旁内角
6.(3分)(2022 贺州)如图,直线a,b被直线c所截,下列各组角是同位角的是( )
A.∠1与∠2 B.∠1与∠3 C.∠2与∠3 D.∠3与∠4
7.(3分)(2022 吉林)如图,如果∠1=∠2,那么AB∥CD,其依据可以简单说成( )
A.两直线平行,内错角相等
B.内错角相等,两直线平行
C.两直线平行,同位角相等
D.同位角相等,两直线平行
8.(3分)(2022 台州)如图,已知∠1=90°,为保证两条铁轨平行,添加的下列条件中,正确的是( )
A.∠2=90° B.∠3=90° C.∠4=90° D.∠5=90°
9.(3分)(2022 资阳)将直尺和三角板按如图所示的位置放置.若∠1=40°,则∠2度数是( )
A.60° B.50° C.40° D.30°
10.(3分)(2022 河池)如图,平行线a,b被直线c所截,若∠1=142°,则∠2的度数是( )
A.142° B.132° C.58° D.38°
11.(3分)(2022 西藏)如图,l1∥l2,∠1=38°,∠2=46°,则∠3的度数为( )
A.46° B.90° C.96° D.134°
12.(3分)(2022 柳州)如图,直线a,b被直线c所截,若a∥b,∠1=70°,则∠2的度数是( )
A.50° B.60° C.70° D.110°
13.(3分)(2022 长沙)如图,AB∥CD,AE∥CF,∠BAE=75°,则∠DCF的度数为( )
A.65° B.70° C.75° D.105°
14.(3分)(2022 恩施州)已知直线l1∥l2,将含30°角的直角三角板按如图所示摆放.若∠1=120°,则∠2=( )
A.120° B.130° C.140° D.150°
15.(3分)(2022 湖北)如图,AB∥CD,直线EF分别交AB,CD于点E,F.∠BEF的平分线交CD于点G.若∠EFG=52°,则∠EGF=( )
A.128° B.64° C.52° D.26°
16.(3分)(2022 随州)如图,直线l1∥l2,直线l与l1,l2相交,若图中∠1=60°,则∠2为( )
A.30° B.40° C.50° D.60°
17.(3分)(2022 威海)如图,在方格纸中,点P,Q,M的坐标分别记为(0,2),(3,0),(1,4).若MN∥PQ,则点N的坐标可能是( )
A.(2,3) B.(3,3) C.(4,2) D.(5,1)
18.(3分)(2022 内蒙古)如图,直线a∥b,截线c,d相交成30°角,∠1=146°33′,则∠2的度数是( )
A.63°27′ B.64°27′ C.64°33′ D.63°33′
19.(3分)(2022 襄阳)已知直线m∥n,将一块含30°角的直角三角板ABC(∠ABC=30°,∠BAC=60°)按如图方式放置,点A,B分别落在直线m,n上.若∠1=70°.则∠2的度数为( )
A.30° B.40° C.60° D.70°
20.(3分)(2022 锦州)如图,直线a∥b,将含30°角的直角三角板ABC(∠ABC=30°)按图中位置摆放,若∠1=110°,则∠2的度数为( )
A.30° B.36° C.40° D.50°
21.(3分)(2022 南通)如图,a∥b,∠3=80°,∠1﹣∠2=20°,则∠1的度数是( )
A.30° B.40° C.50° D.80°
22.(3分)(2022 六盘水)如图,a∥b,∠1=43°,则∠2的度数是( )
A.137° B.53° C.47° D.43°
23.(3分)(2022 兰州)如图,直线a∥b,直线c与直线a,b分别相交于点A,B,AC⊥b,垂足为C.若∠1=52°,则∠2=( )
A.52° B.45° C.38° D.26°
24.(3分)(2022 大连)如图,平行线AB,CD被直线EF所截,FG平分∠EFD,若∠EFD=70°,则∠EGF的度数是( )
A.35° B.55° C.70° D.110°
25.(3分)(2022 盐城)小明将一块直角三角板摆放在直尺上,如图所示,则∠ABC与∠DEF的关系是( )
A.互余 B.互补 C.同位角 D.同旁内角
26.(3分)(2022 营口)如图,直线DE∥FG,Rt△ABC的顶点B,C分别在DE,FG上,若∠BCF=25°,则∠ABE的大小为( )
A.55° B.25° C.65° D.75°
27.(3分)(2022 娄底)一杆古秤在称物时的状态如图所示,已知∠1=80°,则∠2=( )
A.20° B.80° C.100° D.120°
28.(3分)(2022 桂林)如图,直线a,b被直线c所截,且a∥b,若∠1=60°,则∠2的度数是( )
A.70° B.60° C.50° D.40°
29.(3分)(2022 齐齐哈尔)如图所示,直线a∥b,点A在直线a上,点B在直线b上,AC=BC,∠C=120°,∠1=43°,则∠2的度数为( )
A.57° B.63° C.67° D.73°
30.(3分)(2022 山西)如图,Rt△ABC是一块直角三角板,其中∠C=90°,∠BAC=30°.直尺的一边DE经过顶点A,若DE∥CB,则∠DAB的度数为( )
A.100° B.120° C.135° D.150°
31.(3分)(2022 东营)如图,直线a∥b,一个三角板的直角顶点在直线a上,两直角边均与直线b相交,∠1=40°,则∠2=( )
A.40° B.50° C.60° D.65°
32.(3分)(2022 菏泽)如图所示,将一矩形纸片沿AB折叠,已知∠ABC=36°,则∠D1AD=( )
A.48° B.66° C.72° D.78°
33.(3分)(2022 济南)如图,AB∥CD,点E在AB上,EC平分∠AED,若∠1=65°,则∠2的度数为( )
A.45° B.50° C.57.5° D.65°
34.(3分)(2022 丹东)如图,直线l1∥l2,直线l3与l1,l2分别交于A,B两点,过点A作AC⊥l2,垂足为C,若∠1=52°,则∠2的度数是( )
A.32° B.38° C.48° D.52°
35.(3分)(2022 通辽)如图,一束光线AB先后经平面镜OM,ON反射后,反射光线CD与AB平行,当∠ABM=35°时,∠DCN的度数为( )
A.55° B.70° C.60° D.35°
36.(3分)(2022 潍坊)如图是小亮绘制的潜望镜原理示意图,两个平面镜的镜面AB与CD平行,入射光线l与出射光线m平行.若入射光线l与镜面AB的夹角∠1=40°10',则∠6的度数为( )
A.100°40' B.99°80' C.99°40' D.99°20'
37.(3分)(2022 辽宁)如图,直线m∥n,AC⊥BC于点C,∠1=30°,则∠2的度数为( )
A.140° B.130° C.120° D.110°
38.(3分)(2022 台湾)如图为两直线L、M与△ABC相交的情形,其中L、M分别与BC、AB平行.根据图中标示的角度,求∠B的度数为何?( )
A.55 B.60 C.65 D.70
39.(3分)(2022 深圳)一副三角板如图所示放置,斜边平行,则∠1的度数为( )
A.5° B.10° C.15° D.20°
40.(3分)(2022 郴州)如图,直线a∥b,且直线a,b被直线c,d所截,则下列条件不能判定直线c∥d的是( )
A.∠3=∠4 B.∠1+∠5=180° C.∠1=∠2 D.∠1=∠4
【真题汇编】2023年中考数学备考之相交线与平行线(选择题40题)
参考答案与试题解析
一.选择题(共40小题,满分120分,每小题3分)
1.(3分)(2022 北京)如图,利用工具测量角,则∠1的大小为( )
A.30° B.60° C.120° D.150°
【解析】解:根据对顶角相等的性质,可得:∠1=30°,
故选:A.
2.(3分)(2022 河南)如图,直线AB,CD相交于点O,EO⊥CD,垂足为O.若∠1=54°,则∠2的度数为( )
A.26° B.36° C.44° D.54°
【解析】解:∵EO⊥CD,
∴∠COE=90°,
∵∠1+∠COE+∠2=180°,
∴∠2=180°﹣∠1﹣∠COE=180°﹣54°﹣90°=36°.
故选:B.
3.(3分)(2022 威海)图1是光的反射规律示意图.其中,PO是入射光线,OQ是反射光线,法线KO⊥MN,∠POK是入射角,∠KOQ是反射角,∠KOQ=∠POK.图2中,光线自点P射入,经镜面EF反射后经过的点是( )
A.A点 B.B点 C.C点 D.D点
【解析】解:根据直线的性质补全图2并作出法线OK,如下图所示:
根据图形可以看出OB是反射光线,
故选:B.
4.(3分)(2022 常州)如图,斑马线的作用是为了引导行人安全地通过马路.小丽觉得行人沿垂直马路的方向走过斑马线更为合理,这一想法体现的数学依据是( )
A.垂线段最短
B.两点确定一条直线
C.过一点有且只有一条直线与已知直线垂直
D.过直线外一点有且只有一条直线与已知直线平行
【解析】解:小丽觉得行人沿垂直马路的方向走过斑马线更为合理,这一想法体现的数学依据是垂线段最短,
故选:A.
5.(3分)(2022 青海)数学课上老师用双手形象的表示了“三线八角”图形,如图所示(两大拇指代表被截直线,食指代表截线).从左至右依次表示( )
A.同旁内角、同位角、内错角
B.同位角、内错角、对顶角
C.对顶角、同位角、同旁内角
D.同位角、内错角、同旁内角
【解析】解:根据同位角、内错角、同旁内角的概念,可知
第一个图是同位角,第二个图是内错角,第三个图是同旁内角.
故选:D.
6.(3分)(2022 贺州)如图,直线a,b被直线c所截,下列各组角是同位角的是( )
A.∠1与∠2 B.∠1与∠3 C.∠2与∠3 D.∠3与∠4
【解析】解:根据同位角、邻补角、对顶角的定义进行判断,
A、∠1和∠2是对顶角,故A错误;
B、∠1和∠3是同位角,故B正确;
C、∠2和∠3是内错角,故C错误;
D、∠3和∠4是邻补角,故D错误.
故选:B.
7.(3分)(2022 吉林)如图,如果∠1=∠2,那么AB∥CD,其依据可以简单说成( )
A.两直线平行,内错角相等
B.内错角相等,两直线平行
C.两直线平行,同位角相等
D.同位角相等,两直线平行
【解析】解:∵∠1=∠2,
∴AB∥CD(同位角相等,两直线平行),
故选:D.
8.(3分)(2022 台州)如图,已知∠1=90°,为保证两条铁轨平行,添加的下列条件中,正确的是( )
A.∠2=90° B.∠3=90° C.∠4=90° D.∠5=90°
【解析】解:A.由∠2=90°不能判定两条铁轨平行,故该选项不符合题意;
B.由∠3=90°=∠1,可判定两枕木平行,故该选项不符合题意;
C.∵∠1=90°,∠4=90°,
∴∠1=∠4,
∴两条铁轨平行,故该选项符合题意;
D.由∠5=90°不能判定两条铁轨平行,故该选项不符合题意;
故选:C.
9.(3分)(2022 资阳)将直尺和三角板按如图所示的位置放置.若∠1=40°,则∠2度数是( )
A.60° B.50° C.40° D.30°
【解析】解:如图,根据题意可知∠A为直角,直尺的两条边平行,
∴∠2=∠ACB,
∵∠ACB+∠ABC=90°,∠ABC=∠1,
∴∠2=90°﹣∠1=90°﹣40°=50°,
故选:B.
10.(3分)(2022 河池)如图,平行线a,b被直线c所截,若∠1=142°,则∠2的度数是( )
A.142° B.132° C.58° D.38°
【解析】解:∵a∥b,
∴∠2=∠1=142°.
故选:A.
11.(3分)(2022 西藏)如图,l1∥l2,∠1=38°,∠2=46°,则∠3的度数为( )
A.46° B.90° C.96° D.134°
【解析】解:∵l1∥l2,
∴∠1+∠3+∠2=180°,
∵∠1=38°,∠2=46°,
∴∠3=96°,
故选:C.
12.(3分)(2022 柳州)如图,直线a,b被直线c所截,若a∥b,∠1=70°,则∠2的度数是( )
A.50° B.60° C.70° D.110°
【解析】解:∵a∥b,
∴∠2=∠1=70°.
故选:C.
13.(3分)(2022 长沙)如图,AB∥CD,AE∥CF,∠BAE=75°,则∠DCF的度数为( )
A.65° B.70° C.75° D.105°
【解析】解:如图:
∵AB∥CD,
∴∠DGE=∠BAE=75°,
∵AE∥CF,
∴∠DCF=∠DGE=75°,
故选:C.
14.(3分)(2022 恩施州)已知直线l1∥l2,将含30°角的直角三角板按如图所示摆放.若∠1=120°,则∠2=( )
A.120° B.130° C.140° D.150°
【解析】解:过含30°角的直角三角板的直角顶点B作BF∥l1,交AC于点F,
∵∠C=30°,
∴∠A=90°﹣∠C=60°.
∵∠1=∠A+∠ADE,
∴∠ADE=60°.
∵BF∥l1,
∴∠ABF=∠ADE=60°,
∴∠FBG=90°﹣∠ABF=30°.
∵BF∥l1,l1∥l2,
∴BF∥l2,
∴∠BGH+∠FBG=180°,
∴∠BGH=180°﹣∠FBG=150°,
∴∠2=∠BGH=150°.
故选:D.
15.(3分)(2022 湖北)如图,AB∥CD,直线EF分别交AB,CD于点E,F.∠BEF的平分线交CD于点G.若∠EFG=52°,则∠EGF=( )
A.128° B.64° C.52° D.26°
【解析】解:∵AB∥CD,
∴∠FEB=180°﹣∠EFG=128°,
∵EG平分∠BEF,
∴∠BEG=∠BEF=64°,
∵AB∥CD,
∴∠EGF=∠BEG=64°.
故答案选:B.
16.(3分)(2022 随州)如图,直线l1∥l2,直线l与l1,l2相交,若图中∠1=60°,则∠2为( )
A.30° B.40° C.50° D.60°
【解析】解:∵l1∥l2,
∴∠1=∠2,
∵∠1=60°,
∴∠2=60°,
故选:D.
17.(3分)(2022 威海)如图,在方格纸中,点P,Q,M的坐标分别记为(0,2),(3,0),(1,4).若MN∥PQ,则点N的坐标可能是( )
A.(2,3) B.(3,3) C.(4,2) D.(5,1)
【解析】解:如图所示,
∵P(0,2),Q(3,0)M(1,4),
MN∥PQ,
∴N(4,2).
故选:C.
18.(3分)(2022 内蒙古)如图,直线a∥b,截线c,d相交成30°角,∠1=146°33′,则∠2的度数是( )
A.63°27′ B.64°27′ C.64°33′ D.63°33′
27',利用三角形的外角性质即可求∠2.
【解析】解:如图,
∵∠1=146°33′,
∴∠3=180°﹣∠1=33°27',
∵a∥b,
∴∠4=∠3=33°27',
∵∠A=30°,∠2=∠4+∠A,
∴∠2=33°27'+30°=63°27'.
故选:A.
19.(3分)(2022 襄阳)已知直线m∥n,将一块含30°角的直角三角板ABC(∠ABC=30°,∠BAC=60°)按如图方式放置,点A,B分别落在直线m,n上.若∠1=70°.则∠2的度数为( )
A.30° B.40° C.60° D.70°
【解析】解:∵m∥n,∠1=70°,
∴∠1=∠ABD=70°,
∵∠ABC=30°,
∴∠2=∠ABD﹣∠ABC=40°,
故选:B.
20.(3分)(2022 锦州)如图,直线a∥b,将含30°角的直角三角板ABC(∠ABC=30°)按图中位置摆放,若∠1=110°,则∠2的度数为( )
A.30° B.36° C.40° D.50°
【解析】解:如图,
∵a∥b,∠1=110°,
∴∠3=∠1=110°,
∴∠4=180°﹣∠3=70°,
∵∠B=30°
∴∠2=∠4﹣∠B=40°;
故选:C.
21.(3分)(2022 南通)如图,a∥b,∠3=80°,∠1﹣∠2=20°,则∠1的度数是( )
A.30° B.40° C.50° D.80°
【解析】解:如图:
∵a∥b,
∴∠1=∠4,
∵∠3是△ABC的一个外角,
∴∠3=∠4+∠2,
∵∠3=80°,
∴∠1+∠2=80°,
∵∠1﹣∠2=20°,
∴2∠1+∠2﹣∠2=100°,
∴∠1=50°,
故选:C.
22.(3分)(2022 六盘水)如图,a∥b,∠1=43°,则∠2的度数是( )
A.137° B.53° C.47° D.43°
【解析】解:∵a∥b,∠1=43°,
∴∠2=∠1=43°.
故选:D.
23.(3分)(2022 兰州)如图,直线a∥b,直线c与直线a,b分别相交于点A,B,AC⊥b,垂足为C.若∠1=52°,则∠2=( )
A.52° B.45° C.38° D.26°
【解析】解:∵a∥b,
∴∠1=∠ABC=52°,
∵AC⊥b,
∴∠ACB=90°,
∴∠2=90°﹣∠ABC=38°,
故选:C.
24.(3分)(2022 大连)如图,平行线AB,CD被直线EF所截,FG平分∠EFD,若∠EFD=70°,则∠EGF的度数是( )
A.35° B.55° C.70° D.110°
【解析】解:∵FG平分∠EFD,∠EFD=70°,
∴∠GFD=∠EFD=×70°=35°,
∵AB∥CD,
∴∠EGF=∠GFD=35°.
故选:A.
25.(3分)(2022 盐城)小明将一块直角三角板摆放在直尺上,如图所示,则∠ABC与∠DEF的关系是( )
A.互余 B.互补 C.同位角 D.同旁内角
【解析】解:如图,
过点G作GH∥ED,
∵BC∥ED,
∴ED∥GH∥BC,
∴∠ABC=∠AGH,∠DEF=∠HGF,
∵∠HGF+∠AGH=90°,
∴∠ABC+∠DEF=90°
∴∠DEF和∠ABC互余,
故选:A.
26.(3分)(2022 营口)如图,直线DE∥FG,Rt△ABC的顶点B,C分别在DE,FG上,若∠BCF=25°,则∠ABE的大小为( )
A.55° B.25° C.65° D.75°
【解析】解:∵DE∥FG,∠BCF=25°,
∴∠CBE=∠BCF=25°,
∵∠ABC=90°,
∴∠ABE=∠ABC﹣∠CBE=65°.
故选:C.
27.(3分)(2022 娄底)一杆古秤在称物时的状态如图所示,已知∠1=80°,则∠2=( )
A.20° B.80° C.100° D.120°
【解析】解:如图,
由平行线的性质得:∠3=∠1=80°,
∵∠2+∠3=180°,
∴∠2=180°﹣80°=100°.
故选:C.
28.(3分)(2022 桂林)如图,直线a,b被直线c所截,且a∥b,若∠1=60°,则∠2的度数是( )
A.70° B.60° C.50° D.40°
【解析】解:∵a∥b,
∴∠1=∠2,
∵∠1=60°,
∴∠2=60°,
故选:B.
29.(3分)(2022 齐齐哈尔)如图所示,直线a∥b,点A在直线a上,点B在直线b上,AC=BC,∠C=120°,∠1=43°,则∠2的度数为( )
A.57° B.63° C.67° D.73°
【解析】解:∵AC=BC,∠ACB=120°,
∴∠CBA=∠CAB=,
∵a∥b,
∴∠2=∠CBA+∠1=30°+43°=73°.
故选:D.
30.(3分)(2022 山西)如图,Rt△ABC是一块直角三角板,其中∠C=90°,∠BAC=30°.直尺的一边DE经过顶点A,若DE∥CB,则∠DAB的度数为( )
A.100° B.120° C.135° D.150°
【解析】解:∵DE∥CB,∠C=90°,
∴∠DAC=∠C=90°,
∵∠BAC=30°,
∴∠DAB=∠DAC+∠BAC=120°,
故答案为:B.
31.(3分)(2022 东营)如图,直线a∥b,一个三角板的直角顶点在直线a上,两直角边均与直线b相交,∠1=40°,则∠2=( )
A.40° B.50° C.60° D.65°
【解析】解:如图:
∵∠4=90°,∠1=40°,∠1+∠3+∠4=180°,
∴∠3=180°﹣90°﹣40°=50°,
∵直线a∥b,
∴∠2=∠3=50°.
故选:B.
32.(3分)(2022 菏泽)如图所示,将一矩形纸片沿AB折叠,已知∠ABC=36°,则∠D1AD=( )
A.48° B.66° C.72° D.78°
【解析】解:根据题意可得:∠BAD=∠BAD1,
∵矩形纸片的对边平行,即ED∥BC,
∴∠ABC+∠BAD=180°,
∵∠ABC=36°,
∴∠BAD=180°﹣36°=144°,
∴∠BAD1=∠BAD=144°,
∴∠D1AD=360°﹣∠BAD1﹣∠BAD=360°﹣144°﹣144°=72°.
故选:C.
33.(3分)(2022 济南)如图,AB∥CD,点E在AB上,EC平分∠AED,若∠1=65°,则∠2的度数为( )
A.45° B.50° C.57.5° D.65°
【解析】解:∵AB∥CD,
∴∠AEC=∠1=65°.
∵EC平分∠AED,
∴∠AED=2∠AEC=130°.
∴∠2=180°﹣∠AED=50°.
故选:B.
34.(3分)(2022 丹东)如图,直线l1∥l2,直线l3与l1,l2分别交于A,B两点,过点A作AC⊥l2,垂足为C,若∠1=52°,则∠2的度数是( )
A.32° B.38° C.48° D.52°
【解析】解:∵直线l1∥l2,∠1=52°,
∴∠ABC=∠1=52°,
∵AC⊥l2,
∴∠ACB=90°,
∴∠2=180°﹣∠ABC﹣∠ACB=180°﹣52°﹣90°=38°,
故选:B.
35.(3分)(2022 通辽)如图,一束光线AB先后经平面镜OM,ON反射后,反射光线CD与AB平行,当∠ABM=35°时,∠DCN的度数为( )
A.55° B.70° C.60° D.35°
【解析】解:∵∠ABM=35°,∠ABM=∠OBC,
∴∠OBC=35°,
∴∠ABC=180°﹣∠ABM﹣∠OBC=180°﹣35°﹣35°=110°,
∵CD∥AB,
∴∠ABC+∠BCD=180°,
∴∠BCD=180°﹣∠ABC=70°,
∵∠BCO=∠DCN,∠BCO+∠BCD+∠DCN=180°,
∴∠DCN=(180°﹣∠BCD)=55°,
故选:A.
36.(3分)(2022 潍坊)如图是小亮绘制的潜望镜原理示意图,两个平面镜的镜面AB与CD平行,入射光线l与出射光线m平行.若入射光线l与镜面AB的夹角∠1=40°10',则∠6的度数为( )
A.100°40' B.99°80' C.99°40' D.99°20'
【解析】解:∵入射角等于反射角,∠1=40°10',
∴∠2=∠1=40°10',
∵∠1+∠2+∠5=180°,
∴∠5=180°﹣40°10'﹣40°10'=99°40',
∵入射光线l与出射光线m平行,
∴∠6=∠5=99°40'.
故选:C.
37.(3分)(2022 辽宁)如图,直线m∥n,AC⊥BC于点C,∠1=30°,则∠2的度数为( )
A.140° B.130° C.120° D.110°
【解析】解:∵AC⊥BC于点C,
∴∠ACB=90°,
∴∠ABC+∠1=90°,
∴∠ABC=90°﹣30°=60°,
∵m∥n,
∴∠2=180°﹣∠ABC=120°.
故选:C.
38.(3分)(2022 台湾)如图为两直线L、M与△ABC相交的情形,其中L、M分别与BC、AB平行.根据图中标示的角度,求∠B的度数为何?( )
A.55 B.60 C.65 D.70
【解析】解:因为L、M分别与BC、AB平行,
所以∠C+120°=180°,∠A+115°=180°,
所以∠C=60°,∠A=65°,
所以∠B=180°﹣∠C=∠A=55°.
故选:A.
39.(3分)(2022 深圳)一副三角板如图所示放置,斜边平行,则∠1的度数为( )
A.5° B.10° C.15° D.20°
【解析】解:如图,∠ACB=45°,∠F=30°,
∵BC∥EF,
∴∠DCB=∠F=30°,
∴∠1=45°﹣30°=15°,
故选:C.
40.(3分)(2022 郴州)如图,直线a∥b,且直线a,b被直线c,d所截,则下列条件不能判定直线c∥d的是( )
A.∠3=∠4 B.∠1+∠5=180° C.∠1=∠2 D.∠1=∠4
【解析】解:A、若∠3=∠4时,由“内错角相等,两直线平行”可以判定c∥d,不符合题意;
B、若∠1+∠5=180°时,由“同旁内角互补,两直线平行”可以判定c∥d,不符合题意;
C、若∠1=∠2时,由“内错角相等,两直线平行”可以判定a∥b,不能判定c∥d,符合题意;
D、由a∥b推知∠4+∠5=180°.若∠1=∠4时,则∠1+∠5=180°,由“同旁内角互补,两直线平行”可以判定c∥d,不符合题意.
故选:C.
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
