专题19 图形的平移(选择题30题)(含解析)-【冲刺2023中考】真题冲刺专题(知识点+专题训练)
文档属性
| 名称 | 专题19 图形的平移(选择题30题)(含解析)-【冲刺2023中考】真题冲刺专题(知识点+专题训练) |

|
|
| 格式 | doc | ||
| 文件大小 | 587.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-12 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
【真题汇编】2023年中考数学备考之图形的平移
1.平移的性质
(1)平移的条件
平移的方向、平移的距离
(2)平移的性质
①把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同. ②新图形中的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点.连接各组对应点的线段平行且相等.
2.坐标与图形变化-平移
(1)平移变换与坐标变化
①向右平移a个单位,坐标P(x,y) P(x+a,y)
①向左平移a个单位,坐标P(x,y) P(x﹣a,y)
①向上平移b个单位,坐标P(x,y) P(x,y+b)
①向下平移b个单位,坐标P(x,y) P(x,y﹣b)
(2)在平面直角坐标系内,把一个图形各个点的横坐标都加上(或减去)一个整数a,相应的新图形就是把原图形向右(或向左)平移a个单位长度;如果把它各个点的纵坐标都加(或减去)一个整数a,相应的新图形就是把原图形向上(或向下)平移a个单位长度.(即:横坐标,右移加,左移减;纵坐标,上移加,下移减.)
3.利用平移设计图案
确定一个基本图案按照一定的方向平移一定的距离,连续作图即可设计出美丽的图案.
通过改变平移的方向和距离可使图案变得丰富多彩.
【真题汇编】2023年中考数学备考之图形的平移
(选择题30题)
满分:120分 建议时间:100分钟
学校:___________姓名:___________班级:___________考号:___________
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息2.请将答案正确填写在答题卡上
一.选择题(共30小题,满分120分,每小题4分)
1.(4分)(2022 福建)如图,现有一把直尺和一块三角尺,其中∠ABC=90°,∠CAB=60°,AB=8,点A对应直尺的刻度为12.将该三角尺沿着直尺边缘平移,使得△ABC移动到△A′B′C′,点A′对应直尺的刻度为0,则四边形ACC′A′的面积是( )
A.96 B.96 C.192 D.160
2.(4分)(2022 嘉兴)“方胜”是中国古代妇女的一种首饰,其图案由两个全等正方形相叠组成,寓意是同心吉祥.如图,将边长为2cm的正方形ABCD沿对角线BD方向平移1cm得到正方形A′B′C′D′,形成一个“方胜”图案,则点D,B′之间的距离为( )
A.1cm B.2cm C.(﹣1)cm D.(2﹣1)cm
3.(4分)(2022 湖州)如图,将△ABC沿BC方向平移1cm得到对应的△A'B'C'.若B'C=2cm,则BC′的长是( )
A.2cm B.3cm C.4cm D.5cm
4.(4分)(2022 怀化)如图,△ABC沿BC方向平移得到△DEF,已知BC=5,EC=2,则平移的距离是( )
A.1 B.2 C.3 D.4
5.(4分)(2020 上海)如果存在一条线把一个图形分割成两个部分,使其中一个部分沿某个方向平移后能与另一个部分重合,那么我们把这个图形叫做平移重合图形.下列图形中,平移重合图形是( )
A.平行四边形 B.等腰梯形 C.正六边形 D.圆
6.(4分)(2019 枣庄)如图,将△ABC沿BC边上的中线AD平移到△A′B′C′的位置.已知△ABC的面积为16,阴影部分三角形的面积9.若AA′=1,则A′D等于( )
A.2 B.3 C.4 D.
7.(4分)(2020 梧州)点M(2,4)向下平移2个单位长度,得到的点的坐标是( )
A.(2,2) B.(0,2) C.(4,4) D.(2,6)
8.(4分)(2020 自贡)在平面直角坐标系中,将点(2,1)向下平移3个单位长度,所得点的坐标是( )
A.(﹣1,1) B.(5,1) C.(2,4) D.(2,﹣2)
9.(4分)(2019 湘西州)在平面直角坐标系中,将点(2,1)向右平移3个单位长度,则所得的点的坐标是( )
A.(0,5) B.(5,1) C.(2,4) D.(4,2)
10.(4分)(2019 成都)在平面直角坐标系中,将点(﹣2,3)向右平移4个单位长度后得到的点的坐标为( )
A.(2,3) B.(﹣6,3) C.(﹣2,7) D.(﹣2.﹣1)
11.(4分)(2020 台州)如图,把△ABC先向右平移3个单位,再向上平移2个单位得到△DEF,则顶点C(0,﹣1)对应点的坐标为( )
A.(0,0) B.(1,2) C.(1,3) D.(3,1)
12.(4分)(2019 大连)在平面直角坐标系中,将点P(3,1)向下平移2个单位长度,得到的点P′的坐标为( )
A.(3,﹣1) B.(3,3) C.(1,1) D.(5,1)
13.(4分)(2019 海南)如图,在平面直角坐标系中,已知点A(2,1),点B(3,﹣1),平移线段AB,使点A落在点A1(﹣2,2)处,则点B的对应点B1的坐标为( )
A.(﹣1,﹣1) B.(1,0) C.(﹣1,0) D.(3,0)
14.(4分)(2019 黄冈)已知点A的坐标为(2,1),将点A向下平移4个单位长度,得到的点A′的坐标是( )
A.(6,1) B.(﹣2,1) C.(2,5) D.(2,﹣3)
15.(4分)(2021 凉山州)在平面直角坐标系中,将线段AB平移后得到线段A'B',点A(2,1)的对应点A'的坐标为(﹣2,﹣3),则点B(﹣2,3)的对应点B'的坐标为( )
A.(6,1) B.(3,7) C.(﹣6,﹣1) D.(2,﹣1)
16.(4分)(2019 枣庄)在平面直角坐标系中,将点A(1,﹣2)向上平移3个单位长度,再向左平移2个单位长度,得到点A′,则点A′的坐标是( )
A.(﹣1,1) B.(﹣1,﹣2) C.(﹣1,2) D.(1,2)
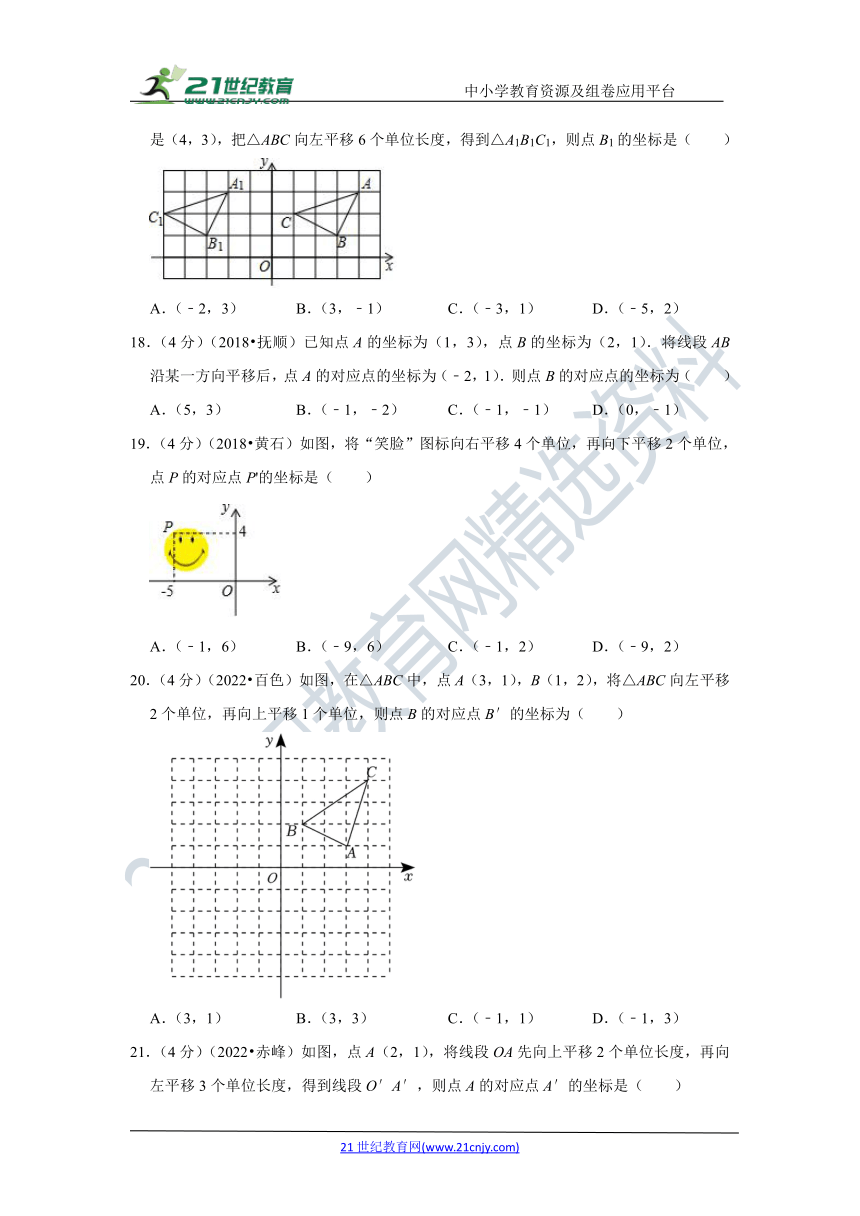
17.(4分)(2018 海南)如图,在平面直角坐标系中,△ABC位于第一象限,点A的坐标是(4,3),把△ABC向左平移6个单位长度,得到△A1B1C1,则点B1的坐标是( )
A.(﹣2,3) B.(3,﹣1) C.(﹣3,1) D.(﹣5,2)
18.(4分)(2018 抚顺)已知点A的坐标为(1,3),点B的坐标为(2,1).将线段AB沿某一方向平移后,点A的对应点的坐标为(﹣2,1).则点B的对应点的坐标为( )
A.(5,3) B.(﹣1,﹣2) C.(﹣1,﹣1) D.(0,﹣1)
19.(4分)(2018 黄石)如图,将“笑脸”图标向右平移4个单位,再向下平移2个单位,点P的对应点P'的坐标是( )
A.(﹣1,6) B.(﹣9,6) C.(﹣1,2) D.(﹣9,2)
20.(4分)(2022 百色)如图,在△ABC中,点A(3,1),B(1,2),将△ABC向左平移2个单位,再向上平移1个单位,则点B的对应点B′的坐标为( )
A.(3,1) B.(3,3) C.(﹣1,1) D.(﹣1,3)
21.(4分)(2022 赤峰)如图,点A(2,1),将线段OA先向上平移2个单位长度,再向左平移3个单位长度,得到线段O′A′,则点A的对应点A′的坐标是( )
A.(﹣3,2) B.(0,4) C.(﹣1,3) D.(3,﹣1)
22.(4分)(2021 日照)在平面直角坐标系中,把点P(﹣3,2)向右平移两个单位后,得到对应点的坐标是( )
A.(﹣5,2) B.(﹣1,4) C.(﹣3,4) D.(﹣1,2)
23.(4分)(2020 成都)在平面直角坐标系中,将点P(3,2)向下平移2个单位长度得到的点的坐标是( )
A.(3,0) B.(1,2) C.(5,2) D.(3,4)
24.(4分)(2020 泸州)在平面直角坐标系中,将点A(﹣2,3)向右平移4个单位长度,得到的对应点A'的坐标为( )
A.(2,7) B.(﹣6,3) C.(2,3) D.(﹣2,﹣1)
25.(4分)(2019 兰州)如图,在平面直角坐标系xOy中,将四边形ABCD先向下平移,再向右平移得到四边形A1B1C1D1,已知A(﹣3,5),B(﹣4,3),A1(3,3),则B1的坐标为( )
A.(1,2) B.(2,1) C.(1,4) D.(4,1)
26.(4分)(2019 滨州)在平面直角坐标系中,将点A(1,﹣2)向上平移3个单位长度,再向左平移2个单位长度,得到点B,则点B的坐标是( )
A.(﹣1,1) B.(3,1) C.(4,﹣4) D.(4,0)
27.(4分)(2022 海南)如图,点A(0,3)、B(1,0),将线段AB平移得到线段DC,若∠ABC=90°,BC=2AB,则点D的坐标是( )
A.(7,2) B.(7,5) C.(5,6) D.(6,5)
28.(4分)(2021 绵阳)如图,在平面直角坐标系中,AB∥DC,AC⊥BC,CD=AD=5,AC=6,将四边形ABCD向左平移m个单位后,点B恰好和原点O重合,则m的值是( )
A.11.4 B.11.6 C.12.4 D.12.6
29.(4分)(2022 广西)2022北京冬残奥会的会徽是以汉字“飞”为灵感来设计的,展现了运动员不断飞跃,超越自我,奋力拼搏,激励世界的冬残奥精神.下列的四个图中,能由如图所示的会徽经过平移得到的是( )
A. B. C. D.
30.(4分)(2019 乐山)下列四个图形中,可以由图通过平移得到的是( )
A. B. C. D.
【真题汇编】2023年中考数学备考之图形的平移(选择题30题)
参考答案与试题解析
一.选择题(共30小题,满分120分,每小题4分)
1.(4分)(2022 福建)如图,现有一把直尺和一块三角尺,其中∠ABC=90°,∠CAB=60°,AB=8,点A对应直尺的刻度为12.将该三角尺沿着直尺边缘平移,使得△ABC移动到△A′B′C′,点A′对应直尺的刻度为0,则四边形ACC′A′的面积是( )
A.96 B.96 C.192 D.160
【解析】解:在Rt△ABC中,∠CAB=60°,AB=8,
则BC=AB tan∠CAB=8,
由平移的性质可知:AC=A′C′,AC∥A′C′,
∴四边形ACC′A′为平行四边形,
∵点A对应直尺的刻度为12,点A′对应直尺的刻度为0,
∴AA′=12,
∴S四边形ACC′A′=12×8=96,
故选:B.
2.(4分)(2022 嘉兴)“方胜”是中国古代妇女的一种首饰,其图案由两个全等正方形相叠组成,寓意是同心吉祥.如图,将边长为2cm的正方形ABCD沿对角线BD方向平移1cm得到正方形A′B′C′D′,形成一个“方胜”图案,则点D,B′之间的距离为( )
A.1cm B.2cm C.(﹣1)cm D.(2﹣1)cm
【解析】解:∵四边形ABCD为边长为2cm的正方形,
∴BD==2(cm),
由平移的性质可知,BB′=1cm,
∴B′D=(2﹣1)cm,
故选:D.
3.(4分)(2022 湖州)如图,将△ABC沿BC方向平移1cm得到对应的△A'B'C'.若B'C=2cm,则BC′的长是( )
A.2cm B.3cm C.4cm D.5cm
【解析】解:∵将△ABC沿BC方向平移1cm得到对应的△A'B'C',
∴BB′=CC′=1(cm),
∵B'C=2(cm),
∴BC′=BB′+B′C+CC′=1+2+1=4(cm),
故选:C.
4.(4分)(2022 怀化)如图,△ABC沿BC方向平移得到△DEF,已知BC=5,EC=2,则平移的距离是( )
A.1 B.2 C.3 D.4
【解析】解:点B平移后对应点是点E.
∴线段BE就是平移距离,
∵已知BC=5,EC=2,
∴BE=BC﹣EC=5﹣2=3.
故选:C.
5.(4分)(2020 上海)如果存在一条线把一个图形分割成两个部分,使其中一个部分沿某个方向平移后能与另一个部分重合,那么我们把这个图形叫做平移重合图形.下列图形中,平移重合图形是( )
A.平行四边形 B.等腰梯形 C.正六边形 D.圆
【解析】解:如图,平行四边形ABCD中,取BC,AD的中点E,F,连接EF.
∵四边形ABEF向右平移可以与四边形EFDC重合,
∴平行四边形ABCD是平移重合图形,
故选:A.
6.(4分)(2019 枣庄)如图,将△ABC沿BC边上的中线AD平移到△A′B′C′的位置.已知△ABC的面积为16,阴影部分三角形的面积9.若AA′=1,则A′D等于( )
A.2 B.3 C.4 D.
【解析】解:设A′B′交BC于E,A′C′交BC于F.
∵S△ABC=16、S△A′EF=9,且AD为BC边的中线,
∴S△A′DE=S△A′EF=,S△ABD=S△ABC=8,
∵将△ABC沿BC边上的中线AD平移得到△A'B'C',
∴A′E∥AB,
∴△DA′E∽△DAB,
则()2=,即()2=,
解得A′D=3或A′D=﹣(舍),
故选:B.
7.(4分)(2020 梧州)点M(2,4)向下平移2个单位长度,得到的点的坐标是( )
A.(2,2) B.(0,2) C.(4,4) D.(2,6)
【解析】解:点M(2,4)向下平移2个单位长度,得到的点的坐标是(2,4﹣2),
即(2,2),
故选:A.
8.(4分)(2020 自贡)在平面直角坐标系中,将点(2,1)向下平移3个单位长度,所得点的坐标是( )
A.(﹣1,1) B.(5,1) C.(2,4) D.(2,﹣2)
【解析】解:将点(2,1)向下平移3个单位长度所得点的坐标为(2,1﹣3),即(2,﹣2);
故选:D.
9.(4分)(2019 湘西州)在平面直角坐标系中,将点(2,1)向右平移3个单位长度,则所得的点的坐标是( )
A.(0,5) B.(5,1) C.(2,4) D.(4,2)
【解析】解:将点(2,1)向右平移3个单位长度,则所得的点的坐标是(5,1).
故选:B.
10.(4分)(2019 成都)在平面直角坐标系中,将点(﹣2,3)向右平移4个单位长度后得到的点的坐标为( )
A.(2,3) B.(﹣6,3) C.(﹣2,7) D.(﹣2.﹣1)
【解析】解:点(﹣2,3)向右平移4个单位长度后得到的点的坐标为(2,3).
故选:A.
11.(4分)(2020 台州)如图,把△ABC先向右平移3个单位,再向上平移2个单位得到△DEF,则顶点C(0,﹣1)对应点的坐标为( )
A.(0,0) B.(1,2) C.(1,3) D.(3,1)
【解析】解:∵把△ABC先向右平移3个单位,再向上平移2个单位得到△DEF,顶点C(0,﹣1),
∴F(0+3,﹣1+2),
即F(3,1),
故选:D.
12.(4分)(2019 大连)在平面直角坐标系中,将点P(3,1)向下平移2个单位长度,得到的点P′的坐标为( )
A.(3,﹣1) B.(3,3) C.(1,1) D.(5,1)
【解析】解:将点P(3,1)向下平移2个单位长度,得到的点P′的坐标为(3,1﹣2),即(3,﹣1),
故选:A.
13.(4分)(2019 海南)如图,在平面直角坐标系中,已知点A(2,1),点B(3,﹣1),平移线段AB,使点A落在点A1(﹣2,2)处,则点B的对应点B1的坐标为( )
A.(﹣1,﹣1) B.(1,0) C.(﹣1,0) D.(3,0)
【解析】解:由点A(2,1)平移后A1(﹣2,2)可得坐标的变化规律是:横坐标﹣4,纵坐标+1,
∴点B的对应点B1的坐标(﹣1,0).
故选:C.
14.(4分)(2019 黄冈)已知点A的坐标为(2,1),将点A向下平移4个单位长度,得到的点A′的坐标是( )
A.(6,1) B.(﹣2,1) C.(2,5) D.(2,﹣3)
【解析】解:∵点A的坐标为(2,1),
∴将点A向下平移4个单位长度,得到的点A′的坐标是(2,﹣3),
故选:D.
15.(4分)(2021 凉山州)在平面直角坐标系中,将线段AB平移后得到线段A'B',点A(2,1)的对应点A'的坐标为(﹣2,﹣3),则点B(﹣2,3)的对应点B'的坐标为( )
A.(6,1) B.(3,7) C.(﹣6,﹣1) D.(2,﹣1)
【解析】解:∵A(2,1)平移后得到点A′的坐标为(﹣2,﹣3),
∴向下平移了4个单位,向左平移了4个单位,
∴B(﹣2,3)的对应点B'的坐标为(﹣2﹣4,3﹣4),
即(﹣6,﹣1).
故选:C.
16.(4分)(2019 枣庄)在平面直角坐标系中,将点A(1,﹣2)向上平移3个单位长度,再向左平移2个单位长度,得到点A′,则点A′的坐标是( )
A.(﹣1,1) B.(﹣1,﹣2) C.(﹣1,2) D.(1,2)
【解析】解:∵将点A(1,﹣2)向上平移3个单位长度,再向左平移2个单位长度,得到点A′,
∴点A′的横坐标为1﹣2=﹣1,纵坐标为﹣2+3=1,
∴A′的坐标为(﹣1,1).
故选:A.
17.(4分)(2018 海南)如图,在平面直角坐标系中,△ABC位于第一象限,点A的坐标是(4,3),把△ABC向左平移6个单位长度,得到△A1B1C1,则点B1的坐标是( )
A.(﹣2,3) B.(3,﹣1) C.(﹣3,1) D.(﹣5,2)
【解析】解:∵点B的坐标为(3,1),
∴向左平移6个单位后,点B1的坐标(﹣3,1),
故选:C.
18.(4分)(2018 抚顺)已知点A的坐标为(1,3),点B的坐标为(2,1).将线段AB沿某一方向平移后,点A的对应点的坐标为(﹣2,1).则点B的对应点的坐标为( )
A.(5,3) B.(﹣1,﹣2) C.(﹣1,﹣1) D.(0,﹣1)
【解析】解:∵A(1,3)的对应点的坐标为(﹣2,1),
∴平移规律为横坐标减3,纵坐标减2,
∴点B(2,1)的对应点的坐标为(﹣1,﹣1).
故选:C.
19.(4分)(2018 黄石)如图,将“笑脸”图标向右平移4个单位,再向下平移2个单位,点P的对应点P'的坐标是( )
A.(﹣1,6) B.(﹣9,6) C.(﹣1,2) D.(﹣9,2)
【解析】解:由题意P(﹣5,4),向右平移4个单位,再向下平移2个单位,点P的对应点P'的坐标是(﹣1,2),
故选:C.
20.(4分)(2022 百色)如图,在△ABC中,点A(3,1),B(1,2),将△ABC向左平移2个单位,再向上平移1个单位,则点B的对应点B′的坐标为( )
A.(3,1) B.(3,3) C.(﹣1,1) D.(﹣1,3)
【解析】解:根据平移与图形变化的规律可知,
将△ABC向左平移2个单位,再向上平移1个单位,其图形上的对应点B′的横坐标减少2,纵坐标增加1,
由于点B(1,2),
所以平移后的对应点B′的坐标为(﹣1,3),
故选:D.
21.(4分)(2022 赤峰)如图,点A(2,1),将线段OA先向上平移2个单位长度,再向左平移3个单位长度,得到线段O′A′,则点A的对应点A′的坐标是( )
A.(﹣3,2) B.(0,4) C.(﹣1,3) D.(3,﹣1)
【解析】解:如图:
由题意得:点A的对应点A′的坐标是(﹣1,3),
故选:C.
22.(4分)(2021 日照)在平面直角坐标系中,把点P(﹣3,2)向右平移两个单位后,得到对应点的坐标是( )
A.(﹣5,2) B.(﹣1,4) C.(﹣3,4) D.(﹣1,2)
【解析】解:根据题意,从点P到点P′,点P′的纵坐标不变,横坐标是﹣3+2=﹣1,
故点P′的坐标是(﹣1,2).
故选:D.
23.(4分)(2020 成都)在平面直角坐标系中,将点P(3,2)向下平移2个单位长度得到的点的坐标是( )
A.(3,0) B.(1,2) C.(5,2) D.(3,4)
【解析】解:将点P(3,2)向下平移2个单位长度所得到的点坐标为(3,2﹣2),即(3,0),
故选:A.
24.(4分)(2020 泸州)在平面直角坐标系中,将点A(﹣2,3)向右平移4个单位长度,得到的对应点A'的坐标为( )
A.(2,7) B.(﹣6,3) C.(2,3) D.(﹣2,﹣1)
【解析】解:∵将点A(﹣2,3)先向右平移4个单位,
∴点A的对应点A′的坐标是(﹣2+4,3),即(2,3).
故选:C.
25.(4分)(2019 兰州)如图,在平面直角坐标系xOy中,将四边形ABCD先向下平移,再向右平移得到四边形A1B1C1D1,已知A(﹣3,5),B(﹣4,3),A1(3,3),则B1的坐标为( )
A.(1,2) B.(2,1) C.(1,4) D.(4,1)
【解析】解:由A(﹣3,5),A1(3,3)可知四边形ABCD先向下平移2个单位,再向右平移6个单位得到四边形A1B1C1D1,
∵B(﹣4,3),
∴B1的坐标为(2,1),
故选:B.
26.(4分)(2019 滨州)在平面直角坐标系中,将点A(1,﹣2)向上平移3个单位长度,再向左平移2个单位长度,得到点B,则点B的坐标是( )
A.(﹣1,1) B.(3,1) C.(4,﹣4) D.(4,0)
【解析】解:∵将点A(1,﹣2)向上平移3个单位长度,再向左平移2个单位长度,得到点B,
∴点B的横坐标为1﹣2=﹣1,纵坐标为﹣2+3=1,
∴B的坐标为(﹣1,1).
故选:A.
27.(4分)(2022 海南)如图,点A(0,3)、B(1,0),将线段AB平移得到线段DC,若∠ABC=90°,BC=2AB,则点D的坐标是( )
A.(7,2) B.(7,5) C.(5,6) D.(6,5)
【解析】解:过点D作DE⊥y轴于点E,如图,
∵点A(0,3)、B(1,0),
∴OA=3,OB=1.
∵线段AB平移得到线段DC,
∴AB∥CD,AB=CD,
∴四边形ABCD是平行四边形,
∵∠ABC=90°,
∴四边形ABCD是矩形.
∴∠BAD=90°,BC=AD.
∵BC=2AB,
∴AD=2AB.
∵∠BAO+∠DAE=90°,∠BAO+∠ABO=90°,
∴∠ABO=∠EAD.
∵∠AOB=∠AED=90°,
∴△ABO∽△DAE.
∴.
∴DE=2OA=6,AE=2OB=2,
∴OE=OA+AE=5,
∴D(6,5).
故选:D.
28.(4分)(2021 绵阳)如图,在平面直角坐标系中,AB∥DC,AC⊥BC,CD=AD=5,AC=6,将四边形ABCD向左平移m个单位后,点B恰好和原点O重合,则m的值是( )
A.11.4 B.11.6 C.12.4 D.12.6
【解析】解:如图,过点D作DT⊥AC交AC于J,交AB于T,连接CT.
∵AD=DC=5,DJ⊥AC,
∴AJ=JC=3,
∴DJ===4,
∵CD∥AT.
∴∠DCJ=∠TAJ,
∵∠DJC=∠TJA,
∴△DCJ≌△TAJ(ASA),
∴CD=AT=5,DJ=JT=4,
∵∠AJT=∠ACB=90°,
∴JT∥BC,
∵AJ=JC,
∴AT=TB=5,
设OA=x,∵OD2=AD2﹣OA2=DT2﹣OT2,
∴52﹣x2=82﹣(x+5)2,
解得x=1.4,
∴OB=OA+AB=1.4+10=11.4,
∵将四边形ABCD向左平移m个单位后,点B恰好和原点O重合,
∴m=OB=11.4,
故选:A.
29.(4分)(2022 广西)2022北京冬残奥会的会徽是以汉字“飞”为灵感来设计的,展现了运动员不断飞跃,超越自我,奋力拼搏,激励世界的冬残奥精神.下列的四个图中,能由如图所示的会徽经过平移得到的是( )
A. B. C. D.
【解析】解:根据平移的性质可知:能由如图经过平移得到的是D,
故选:D.
30.(4分)(2019 乐山)下列四个图形中,可以由图通过平移得到的是( )
A. B. C. D.
【解析】解:只有D的图形的形状和大小没有变化,符合平移的性质,属于平移得到;
故选:D.
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
【真题汇编】2023年中考数学备考之图形的平移
1.平移的性质
(1)平移的条件
平移的方向、平移的距离
(2)平移的性质
①把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同. ②新图形中的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点.连接各组对应点的线段平行且相等.
2.坐标与图形变化-平移
(1)平移变换与坐标变化
①向右平移a个单位,坐标P(x,y) P(x+a,y)
①向左平移a个单位,坐标P(x,y) P(x﹣a,y)
①向上平移b个单位,坐标P(x,y) P(x,y+b)
①向下平移b个单位,坐标P(x,y) P(x,y﹣b)
(2)在平面直角坐标系内,把一个图形各个点的横坐标都加上(或减去)一个整数a,相应的新图形就是把原图形向右(或向左)平移a个单位长度;如果把它各个点的纵坐标都加(或减去)一个整数a,相应的新图形就是把原图形向上(或向下)平移a个单位长度.(即:横坐标,右移加,左移减;纵坐标,上移加,下移减.)
3.利用平移设计图案
确定一个基本图案按照一定的方向平移一定的距离,连续作图即可设计出美丽的图案.
通过改变平移的方向和距离可使图案变得丰富多彩.
【真题汇编】2023年中考数学备考之图形的平移
(选择题30题)
满分:120分 建议时间:100分钟
学校:___________姓名:___________班级:___________考号:___________
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息2.请将答案正确填写在答题卡上
一.选择题(共30小题,满分120分,每小题4分)
1.(4分)(2022 福建)如图,现有一把直尺和一块三角尺,其中∠ABC=90°,∠CAB=60°,AB=8,点A对应直尺的刻度为12.将该三角尺沿着直尺边缘平移,使得△ABC移动到△A′B′C′,点A′对应直尺的刻度为0,则四边形ACC′A′的面积是( )
A.96 B.96 C.192 D.160
2.(4分)(2022 嘉兴)“方胜”是中国古代妇女的一种首饰,其图案由两个全等正方形相叠组成,寓意是同心吉祥.如图,将边长为2cm的正方形ABCD沿对角线BD方向平移1cm得到正方形A′B′C′D′,形成一个“方胜”图案,则点D,B′之间的距离为( )
A.1cm B.2cm C.(﹣1)cm D.(2﹣1)cm
3.(4分)(2022 湖州)如图,将△ABC沿BC方向平移1cm得到对应的△A'B'C'.若B'C=2cm,则BC′的长是( )
A.2cm B.3cm C.4cm D.5cm
4.(4分)(2022 怀化)如图,△ABC沿BC方向平移得到△DEF,已知BC=5,EC=2,则平移的距离是( )
A.1 B.2 C.3 D.4
5.(4分)(2020 上海)如果存在一条线把一个图形分割成两个部分,使其中一个部分沿某个方向平移后能与另一个部分重合,那么我们把这个图形叫做平移重合图形.下列图形中,平移重合图形是( )
A.平行四边形 B.等腰梯形 C.正六边形 D.圆
6.(4分)(2019 枣庄)如图,将△ABC沿BC边上的中线AD平移到△A′B′C′的位置.已知△ABC的面积为16,阴影部分三角形的面积9.若AA′=1,则A′D等于( )
A.2 B.3 C.4 D.
7.(4分)(2020 梧州)点M(2,4)向下平移2个单位长度,得到的点的坐标是( )
A.(2,2) B.(0,2) C.(4,4) D.(2,6)
8.(4分)(2020 自贡)在平面直角坐标系中,将点(2,1)向下平移3个单位长度,所得点的坐标是( )
A.(﹣1,1) B.(5,1) C.(2,4) D.(2,﹣2)
9.(4分)(2019 湘西州)在平面直角坐标系中,将点(2,1)向右平移3个单位长度,则所得的点的坐标是( )
A.(0,5) B.(5,1) C.(2,4) D.(4,2)
10.(4分)(2019 成都)在平面直角坐标系中,将点(﹣2,3)向右平移4个单位长度后得到的点的坐标为( )
A.(2,3) B.(﹣6,3) C.(﹣2,7) D.(﹣2.﹣1)
11.(4分)(2020 台州)如图,把△ABC先向右平移3个单位,再向上平移2个单位得到△DEF,则顶点C(0,﹣1)对应点的坐标为( )
A.(0,0) B.(1,2) C.(1,3) D.(3,1)
12.(4分)(2019 大连)在平面直角坐标系中,将点P(3,1)向下平移2个单位长度,得到的点P′的坐标为( )
A.(3,﹣1) B.(3,3) C.(1,1) D.(5,1)
13.(4分)(2019 海南)如图,在平面直角坐标系中,已知点A(2,1),点B(3,﹣1),平移线段AB,使点A落在点A1(﹣2,2)处,则点B的对应点B1的坐标为( )
A.(﹣1,﹣1) B.(1,0) C.(﹣1,0) D.(3,0)
14.(4分)(2019 黄冈)已知点A的坐标为(2,1),将点A向下平移4个单位长度,得到的点A′的坐标是( )
A.(6,1) B.(﹣2,1) C.(2,5) D.(2,﹣3)
15.(4分)(2021 凉山州)在平面直角坐标系中,将线段AB平移后得到线段A'B',点A(2,1)的对应点A'的坐标为(﹣2,﹣3),则点B(﹣2,3)的对应点B'的坐标为( )
A.(6,1) B.(3,7) C.(﹣6,﹣1) D.(2,﹣1)
16.(4分)(2019 枣庄)在平面直角坐标系中,将点A(1,﹣2)向上平移3个单位长度,再向左平移2个单位长度,得到点A′,则点A′的坐标是( )
A.(﹣1,1) B.(﹣1,﹣2) C.(﹣1,2) D.(1,2)
17.(4分)(2018 海南)如图,在平面直角坐标系中,△ABC位于第一象限,点A的坐标是(4,3),把△ABC向左平移6个单位长度,得到△A1B1C1,则点B1的坐标是( )
A.(﹣2,3) B.(3,﹣1) C.(﹣3,1) D.(﹣5,2)
18.(4分)(2018 抚顺)已知点A的坐标为(1,3),点B的坐标为(2,1).将线段AB沿某一方向平移后,点A的对应点的坐标为(﹣2,1).则点B的对应点的坐标为( )
A.(5,3) B.(﹣1,﹣2) C.(﹣1,﹣1) D.(0,﹣1)
19.(4分)(2018 黄石)如图,将“笑脸”图标向右平移4个单位,再向下平移2个单位,点P的对应点P'的坐标是( )
A.(﹣1,6) B.(﹣9,6) C.(﹣1,2) D.(﹣9,2)
20.(4分)(2022 百色)如图,在△ABC中,点A(3,1),B(1,2),将△ABC向左平移2个单位,再向上平移1个单位,则点B的对应点B′的坐标为( )
A.(3,1) B.(3,3) C.(﹣1,1) D.(﹣1,3)
21.(4分)(2022 赤峰)如图,点A(2,1),将线段OA先向上平移2个单位长度,再向左平移3个单位长度,得到线段O′A′,则点A的对应点A′的坐标是( )
A.(﹣3,2) B.(0,4) C.(﹣1,3) D.(3,﹣1)
22.(4分)(2021 日照)在平面直角坐标系中,把点P(﹣3,2)向右平移两个单位后,得到对应点的坐标是( )
A.(﹣5,2) B.(﹣1,4) C.(﹣3,4) D.(﹣1,2)
23.(4分)(2020 成都)在平面直角坐标系中,将点P(3,2)向下平移2个单位长度得到的点的坐标是( )
A.(3,0) B.(1,2) C.(5,2) D.(3,4)
24.(4分)(2020 泸州)在平面直角坐标系中,将点A(﹣2,3)向右平移4个单位长度,得到的对应点A'的坐标为( )
A.(2,7) B.(﹣6,3) C.(2,3) D.(﹣2,﹣1)
25.(4分)(2019 兰州)如图,在平面直角坐标系xOy中,将四边形ABCD先向下平移,再向右平移得到四边形A1B1C1D1,已知A(﹣3,5),B(﹣4,3),A1(3,3),则B1的坐标为( )
A.(1,2) B.(2,1) C.(1,4) D.(4,1)
26.(4分)(2019 滨州)在平面直角坐标系中,将点A(1,﹣2)向上平移3个单位长度,再向左平移2个单位长度,得到点B,则点B的坐标是( )
A.(﹣1,1) B.(3,1) C.(4,﹣4) D.(4,0)
27.(4分)(2022 海南)如图,点A(0,3)、B(1,0),将线段AB平移得到线段DC,若∠ABC=90°,BC=2AB,则点D的坐标是( )
A.(7,2) B.(7,5) C.(5,6) D.(6,5)
28.(4分)(2021 绵阳)如图,在平面直角坐标系中,AB∥DC,AC⊥BC,CD=AD=5,AC=6,将四边形ABCD向左平移m个单位后,点B恰好和原点O重合,则m的值是( )
A.11.4 B.11.6 C.12.4 D.12.6
29.(4分)(2022 广西)2022北京冬残奥会的会徽是以汉字“飞”为灵感来设计的,展现了运动员不断飞跃,超越自我,奋力拼搏,激励世界的冬残奥精神.下列的四个图中,能由如图所示的会徽经过平移得到的是( )
A. B. C. D.
30.(4分)(2019 乐山)下列四个图形中,可以由图通过平移得到的是( )
A. B. C. D.
【真题汇编】2023年中考数学备考之图形的平移(选择题30题)
参考答案与试题解析
一.选择题(共30小题,满分120分,每小题4分)
1.(4分)(2022 福建)如图,现有一把直尺和一块三角尺,其中∠ABC=90°,∠CAB=60°,AB=8,点A对应直尺的刻度为12.将该三角尺沿着直尺边缘平移,使得△ABC移动到△A′B′C′,点A′对应直尺的刻度为0,则四边形ACC′A′的面积是( )
A.96 B.96 C.192 D.160
【解析】解:在Rt△ABC中,∠CAB=60°,AB=8,
则BC=AB tan∠CAB=8,
由平移的性质可知:AC=A′C′,AC∥A′C′,
∴四边形ACC′A′为平行四边形,
∵点A对应直尺的刻度为12,点A′对应直尺的刻度为0,
∴AA′=12,
∴S四边形ACC′A′=12×8=96,
故选:B.
2.(4分)(2022 嘉兴)“方胜”是中国古代妇女的一种首饰,其图案由两个全等正方形相叠组成,寓意是同心吉祥.如图,将边长为2cm的正方形ABCD沿对角线BD方向平移1cm得到正方形A′B′C′D′,形成一个“方胜”图案,则点D,B′之间的距离为( )
A.1cm B.2cm C.(﹣1)cm D.(2﹣1)cm
【解析】解:∵四边形ABCD为边长为2cm的正方形,
∴BD==2(cm),
由平移的性质可知,BB′=1cm,
∴B′D=(2﹣1)cm,
故选:D.
3.(4分)(2022 湖州)如图,将△ABC沿BC方向平移1cm得到对应的△A'B'C'.若B'C=2cm,则BC′的长是( )
A.2cm B.3cm C.4cm D.5cm
【解析】解:∵将△ABC沿BC方向平移1cm得到对应的△A'B'C',
∴BB′=CC′=1(cm),
∵B'C=2(cm),
∴BC′=BB′+B′C+CC′=1+2+1=4(cm),
故选:C.
4.(4分)(2022 怀化)如图,△ABC沿BC方向平移得到△DEF,已知BC=5,EC=2,则平移的距离是( )
A.1 B.2 C.3 D.4
【解析】解:点B平移后对应点是点E.
∴线段BE就是平移距离,
∵已知BC=5,EC=2,
∴BE=BC﹣EC=5﹣2=3.
故选:C.
5.(4分)(2020 上海)如果存在一条线把一个图形分割成两个部分,使其中一个部分沿某个方向平移后能与另一个部分重合,那么我们把这个图形叫做平移重合图形.下列图形中,平移重合图形是( )
A.平行四边形 B.等腰梯形 C.正六边形 D.圆
【解析】解:如图,平行四边形ABCD中,取BC,AD的中点E,F,连接EF.
∵四边形ABEF向右平移可以与四边形EFDC重合,
∴平行四边形ABCD是平移重合图形,
故选:A.
6.(4分)(2019 枣庄)如图,将△ABC沿BC边上的中线AD平移到△A′B′C′的位置.已知△ABC的面积为16,阴影部分三角形的面积9.若AA′=1,则A′D等于( )
A.2 B.3 C.4 D.
【解析】解:设A′B′交BC于E,A′C′交BC于F.
∵S△ABC=16、S△A′EF=9,且AD为BC边的中线,
∴S△A′DE=S△A′EF=,S△ABD=S△ABC=8,
∵将△ABC沿BC边上的中线AD平移得到△A'B'C',
∴A′E∥AB,
∴△DA′E∽△DAB,
则()2=,即()2=,
解得A′D=3或A′D=﹣(舍),
故选:B.
7.(4分)(2020 梧州)点M(2,4)向下平移2个单位长度,得到的点的坐标是( )
A.(2,2) B.(0,2) C.(4,4) D.(2,6)
【解析】解:点M(2,4)向下平移2个单位长度,得到的点的坐标是(2,4﹣2),
即(2,2),
故选:A.
8.(4分)(2020 自贡)在平面直角坐标系中,将点(2,1)向下平移3个单位长度,所得点的坐标是( )
A.(﹣1,1) B.(5,1) C.(2,4) D.(2,﹣2)
【解析】解:将点(2,1)向下平移3个单位长度所得点的坐标为(2,1﹣3),即(2,﹣2);
故选:D.
9.(4分)(2019 湘西州)在平面直角坐标系中,将点(2,1)向右平移3个单位长度,则所得的点的坐标是( )
A.(0,5) B.(5,1) C.(2,4) D.(4,2)
【解析】解:将点(2,1)向右平移3个单位长度,则所得的点的坐标是(5,1).
故选:B.
10.(4分)(2019 成都)在平面直角坐标系中,将点(﹣2,3)向右平移4个单位长度后得到的点的坐标为( )
A.(2,3) B.(﹣6,3) C.(﹣2,7) D.(﹣2.﹣1)
【解析】解:点(﹣2,3)向右平移4个单位长度后得到的点的坐标为(2,3).
故选:A.
11.(4分)(2020 台州)如图,把△ABC先向右平移3个单位,再向上平移2个单位得到△DEF,则顶点C(0,﹣1)对应点的坐标为( )
A.(0,0) B.(1,2) C.(1,3) D.(3,1)
【解析】解:∵把△ABC先向右平移3个单位,再向上平移2个单位得到△DEF,顶点C(0,﹣1),
∴F(0+3,﹣1+2),
即F(3,1),
故选:D.
12.(4分)(2019 大连)在平面直角坐标系中,将点P(3,1)向下平移2个单位长度,得到的点P′的坐标为( )
A.(3,﹣1) B.(3,3) C.(1,1) D.(5,1)
【解析】解:将点P(3,1)向下平移2个单位长度,得到的点P′的坐标为(3,1﹣2),即(3,﹣1),
故选:A.
13.(4分)(2019 海南)如图,在平面直角坐标系中,已知点A(2,1),点B(3,﹣1),平移线段AB,使点A落在点A1(﹣2,2)处,则点B的对应点B1的坐标为( )
A.(﹣1,﹣1) B.(1,0) C.(﹣1,0) D.(3,0)
【解析】解:由点A(2,1)平移后A1(﹣2,2)可得坐标的变化规律是:横坐标﹣4,纵坐标+1,
∴点B的对应点B1的坐标(﹣1,0).
故选:C.
14.(4分)(2019 黄冈)已知点A的坐标为(2,1),将点A向下平移4个单位长度,得到的点A′的坐标是( )
A.(6,1) B.(﹣2,1) C.(2,5) D.(2,﹣3)
【解析】解:∵点A的坐标为(2,1),
∴将点A向下平移4个单位长度,得到的点A′的坐标是(2,﹣3),
故选:D.
15.(4分)(2021 凉山州)在平面直角坐标系中,将线段AB平移后得到线段A'B',点A(2,1)的对应点A'的坐标为(﹣2,﹣3),则点B(﹣2,3)的对应点B'的坐标为( )
A.(6,1) B.(3,7) C.(﹣6,﹣1) D.(2,﹣1)
【解析】解:∵A(2,1)平移后得到点A′的坐标为(﹣2,﹣3),
∴向下平移了4个单位,向左平移了4个单位,
∴B(﹣2,3)的对应点B'的坐标为(﹣2﹣4,3﹣4),
即(﹣6,﹣1).
故选:C.
16.(4分)(2019 枣庄)在平面直角坐标系中,将点A(1,﹣2)向上平移3个单位长度,再向左平移2个单位长度,得到点A′,则点A′的坐标是( )
A.(﹣1,1) B.(﹣1,﹣2) C.(﹣1,2) D.(1,2)
【解析】解:∵将点A(1,﹣2)向上平移3个单位长度,再向左平移2个单位长度,得到点A′,
∴点A′的横坐标为1﹣2=﹣1,纵坐标为﹣2+3=1,
∴A′的坐标为(﹣1,1).
故选:A.
17.(4分)(2018 海南)如图,在平面直角坐标系中,△ABC位于第一象限,点A的坐标是(4,3),把△ABC向左平移6个单位长度,得到△A1B1C1,则点B1的坐标是( )
A.(﹣2,3) B.(3,﹣1) C.(﹣3,1) D.(﹣5,2)
【解析】解:∵点B的坐标为(3,1),
∴向左平移6个单位后,点B1的坐标(﹣3,1),
故选:C.
18.(4分)(2018 抚顺)已知点A的坐标为(1,3),点B的坐标为(2,1).将线段AB沿某一方向平移后,点A的对应点的坐标为(﹣2,1).则点B的对应点的坐标为( )
A.(5,3) B.(﹣1,﹣2) C.(﹣1,﹣1) D.(0,﹣1)
【解析】解:∵A(1,3)的对应点的坐标为(﹣2,1),
∴平移规律为横坐标减3,纵坐标减2,
∴点B(2,1)的对应点的坐标为(﹣1,﹣1).
故选:C.
19.(4分)(2018 黄石)如图,将“笑脸”图标向右平移4个单位,再向下平移2个单位,点P的对应点P'的坐标是( )
A.(﹣1,6) B.(﹣9,6) C.(﹣1,2) D.(﹣9,2)
【解析】解:由题意P(﹣5,4),向右平移4个单位,再向下平移2个单位,点P的对应点P'的坐标是(﹣1,2),
故选:C.
20.(4分)(2022 百色)如图,在△ABC中,点A(3,1),B(1,2),将△ABC向左平移2个单位,再向上平移1个单位,则点B的对应点B′的坐标为( )
A.(3,1) B.(3,3) C.(﹣1,1) D.(﹣1,3)
【解析】解:根据平移与图形变化的规律可知,
将△ABC向左平移2个单位,再向上平移1个单位,其图形上的对应点B′的横坐标减少2,纵坐标增加1,
由于点B(1,2),
所以平移后的对应点B′的坐标为(﹣1,3),
故选:D.
21.(4分)(2022 赤峰)如图,点A(2,1),将线段OA先向上平移2个单位长度,再向左平移3个单位长度,得到线段O′A′,则点A的对应点A′的坐标是( )
A.(﹣3,2) B.(0,4) C.(﹣1,3) D.(3,﹣1)
【解析】解:如图:
由题意得:点A的对应点A′的坐标是(﹣1,3),
故选:C.
22.(4分)(2021 日照)在平面直角坐标系中,把点P(﹣3,2)向右平移两个单位后,得到对应点的坐标是( )
A.(﹣5,2) B.(﹣1,4) C.(﹣3,4) D.(﹣1,2)
【解析】解:根据题意,从点P到点P′,点P′的纵坐标不变,横坐标是﹣3+2=﹣1,
故点P′的坐标是(﹣1,2).
故选:D.
23.(4分)(2020 成都)在平面直角坐标系中,将点P(3,2)向下平移2个单位长度得到的点的坐标是( )
A.(3,0) B.(1,2) C.(5,2) D.(3,4)
【解析】解:将点P(3,2)向下平移2个单位长度所得到的点坐标为(3,2﹣2),即(3,0),
故选:A.
24.(4分)(2020 泸州)在平面直角坐标系中,将点A(﹣2,3)向右平移4个单位长度,得到的对应点A'的坐标为( )
A.(2,7) B.(﹣6,3) C.(2,3) D.(﹣2,﹣1)
【解析】解:∵将点A(﹣2,3)先向右平移4个单位,
∴点A的对应点A′的坐标是(﹣2+4,3),即(2,3).
故选:C.
25.(4分)(2019 兰州)如图,在平面直角坐标系xOy中,将四边形ABCD先向下平移,再向右平移得到四边形A1B1C1D1,已知A(﹣3,5),B(﹣4,3),A1(3,3),则B1的坐标为( )
A.(1,2) B.(2,1) C.(1,4) D.(4,1)
【解析】解:由A(﹣3,5),A1(3,3)可知四边形ABCD先向下平移2个单位,再向右平移6个单位得到四边形A1B1C1D1,
∵B(﹣4,3),
∴B1的坐标为(2,1),
故选:B.
26.(4分)(2019 滨州)在平面直角坐标系中,将点A(1,﹣2)向上平移3个单位长度,再向左平移2个单位长度,得到点B,则点B的坐标是( )
A.(﹣1,1) B.(3,1) C.(4,﹣4) D.(4,0)
【解析】解:∵将点A(1,﹣2)向上平移3个单位长度,再向左平移2个单位长度,得到点B,
∴点B的横坐标为1﹣2=﹣1,纵坐标为﹣2+3=1,
∴B的坐标为(﹣1,1).
故选:A.
27.(4分)(2022 海南)如图,点A(0,3)、B(1,0),将线段AB平移得到线段DC,若∠ABC=90°,BC=2AB,则点D的坐标是( )
A.(7,2) B.(7,5) C.(5,6) D.(6,5)
【解析】解:过点D作DE⊥y轴于点E,如图,
∵点A(0,3)、B(1,0),
∴OA=3,OB=1.
∵线段AB平移得到线段DC,
∴AB∥CD,AB=CD,
∴四边形ABCD是平行四边形,
∵∠ABC=90°,
∴四边形ABCD是矩形.
∴∠BAD=90°,BC=AD.
∵BC=2AB,
∴AD=2AB.
∵∠BAO+∠DAE=90°,∠BAO+∠ABO=90°,
∴∠ABO=∠EAD.
∵∠AOB=∠AED=90°,
∴△ABO∽△DAE.
∴.
∴DE=2OA=6,AE=2OB=2,
∴OE=OA+AE=5,
∴D(6,5).
故选:D.
28.(4分)(2021 绵阳)如图,在平面直角坐标系中,AB∥DC,AC⊥BC,CD=AD=5,AC=6,将四边形ABCD向左平移m个单位后,点B恰好和原点O重合,则m的值是( )
A.11.4 B.11.6 C.12.4 D.12.6
【解析】解:如图,过点D作DT⊥AC交AC于J,交AB于T,连接CT.
∵AD=DC=5,DJ⊥AC,
∴AJ=JC=3,
∴DJ===4,
∵CD∥AT.
∴∠DCJ=∠TAJ,
∵∠DJC=∠TJA,
∴△DCJ≌△TAJ(ASA),
∴CD=AT=5,DJ=JT=4,
∵∠AJT=∠ACB=90°,
∴JT∥BC,
∵AJ=JC,
∴AT=TB=5,
设OA=x,∵OD2=AD2﹣OA2=DT2﹣OT2,
∴52﹣x2=82﹣(x+5)2,
解得x=1.4,
∴OB=OA+AB=1.4+10=11.4,
∵将四边形ABCD向左平移m个单位后,点B恰好和原点O重合,
∴m=OB=11.4,
故选:A.
29.(4分)(2022 广西)2022北京冬残奥会的会徽是以汉字“飞”为灵感来设计的,展现了运动员不断飞跃,超越自我,奋力拼搏,激励世界的冬残奥精神.下列的四个图中,能由如图所示的会徽经过平移得到的是( )
A. B. C. D.
【解析】解:根据平移的性质可知:能由如图经过平移得到的是D,
故选:D.
30.(4分)(2019 乐山)下列四个图形中,可以由图通过平移得到的是( )
A. B. C. D.
【解析】解:只有D的图形的形状和大小没有变化,符合平移的性质,属于平移得到;
故选:D.
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
