专题25 锐角三角函数(选择题40题)(含解析)-【冲刺2023中考】真题冲刺专题(知识点+专题训练)
文档属性
| 名称 | 专题25 锐角三角函数(选择题40题)(含解析)-【冲刺2023中考】真题冲刺专题(知识点+专题训练) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-12 10:13:11 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
【真题汇编】2023年中考数学备考之锐角三角函数
1.锐角三角函数的定义
在Rt△ABC中,∠C=90°.
(1)正弦:我们把锐角A的对边a与斜边c的比叫做∠A的正弦,记作sinA.
即sinA=∠A的对边除以斜边=.
(2)余弦:锐角A的邻边b与斜边c的比叫做∠A的余弦,记作cosA.
即cosA=∠A的邻边除以斜边=.
(3)正切:锐角A的对边a与邻边b的比叫做∠A的正切,记作tanA.
即tanA=∠A的对边除以∠A的邻边=.
(4)三角函数:锐角A的正弦、余弦、正切都叫做∠A的锐角三角函数.
2.特殊角的三角函数值
(1)特指30°、45°、60°角的各种三角函数值.
sin30°=; cos30°=;tan30°=;
sin45°=;cos45°=;tan45°=1;
sin60°=;cos60°=; tan60°=;
(2)应用中要熟记特殊角的三角函数值,一是按值的变化规律去记,正弦逐渐增大,余弦逐渐减小,正切逐渐增大;二是按特殊直角三角形中各边特殊值规律去记.
(3)特殊角的三角函数值应用广泛,一是它可以当作数进行运算,二是具有三角函数的特点,在解直角三角形中应用较多.
3.计算器—三角函数
(1)用计算器可以求出任意锐角的三角函数值,也可以根据三角函数值求出锐角的度数.
(2)求锐角三角函数值的方法:
如求tan46°35′的值时,先按键“tan”,再输入角的度数46°35′,按键“=”即可得到结果.
注意:不同型号的计算器使用方法不同.
(3)已知锐角三角函数值求锐角的方法是:
如已知sinα=0.5678,一般先按键“2ndF”,再按键“sin”,输入“0.5678”,再按键“=”即可得到结果.
注意:一般情况下,三角函数值直接可以求出,已知三角函数值求角需要用第二功能键.
4.解直角三角形
(1)解直角三角形的定义
在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.
(2)解直角三角形要用到的关系
①锐角、直角之间的关系:∠A+∠B=90°;
②三边之间的关系:a2+b2=c2;
③边角之间的关系:
sinA==,cosA==,tanA==.
(a,b,c分别是∠A、∠B、∠C的对边)
5.解直角三角形的应用
(1)通过解直角三角形能解决实际问题中的很多有关测量问.
如:测不易直接测量的物体的高度、测河宽等,关键在于构造出直角三角形,通过测量角的度数和测量边的长度,计算出所要求的物体的高度或长度.
(2)解直角三角形的一般过程是:
①将实际问题抽象为数学问题(画出平面图形,构造出直角三角形转化为解直角三角形问题).
②根据题目已知特点选用适当锐角三角函数或边角关系去解直角三角形,得到数学问题的答案,再转化得到实际问题的答案.
6.解直角三角形的应用-坡度坡角问题
(1)坡度是坡面的铅直高度h和水平宽度l的比,又叫做坡比,它是一个比值,反映了斜坡的陡峭程度,一般用i表示,常写成i=1:m的形式.
(2)把坡面与水平面的夹角α叫做坡角,坡度i与坡角α之间的关系为:i=h/l=tanα.
(3)在解决坡度的有关问题中,一般通过作高构成直角三角形,坡角即是一锐角,坡度实际就是一锐角的正切值,水平宽度或铅直高度都是直角边,实质也是解直角三角形问题.
应用领域:①测量领域;②航空领域 ③航海领域:④工程领域等.
7.解直角三角形的应用-仰角俯角问题
(1)概念:仰角是向上看的视线与水平线的夹角;俯角是向下看的视线与水平线的夹角.
(2)解决此类问题要了解角之间的关系,找到与已知和未知相关联的直角三角形,当图形中没有直角三角形时,要通过作高或垂线构造直角三角形,另当问题以一个实际问题的形式给出时,要善于读懂题意,把实际问题划归为直角三角形中边角关系问题加以解决.
【真题汇编】2023年中考数学备考之锐角三角函数
(选择题40题)
满分:120分 建议时间:100分钟
学校:___________姓名:___________班级:___________考号:___________
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息2.请将答案正确填写在答题卡上
一.选择题(共40小题,满分120分,每小题3分)
1.(3分)(2022 荆州)如图,在平面直角坐标系中,点A,B分别在x轴负半轴和y轴正半轴上,点C在OB上,OC:BC=1:2,连接AC,过点O作OP∥AB交AC的延长线于P.若P(1,1),则tan∠OAP的值是( )
A. B. C. D.3
2.(3分)(2022 天津)tan45°的值等于( )
A.2 B.1 C. D.
3.(3分)(2021 烟台)如图所示,若用我们数学课本上采用的科学计算器进行计算,其按键顺序及结果如下:
按键的结果为m;
按键的结果为n;
按键的结果为k.
下列判断正确的是( )
A.m=n B.n=k C.m=k D.m=n=k
4.(3分)(2021 威海)若用我们数学课本上采用的科学计算器计算sin36°18′,按键顺序正确的是( )
A.
B.
C.
D.
5.(3分)(2021 东营)如图,在△ABC中,∠C=90°,∠B=42°,BC=8,若用科学计算器求AC的长,则下列按键顺序正确的是( )
A.
B.
C.
D.
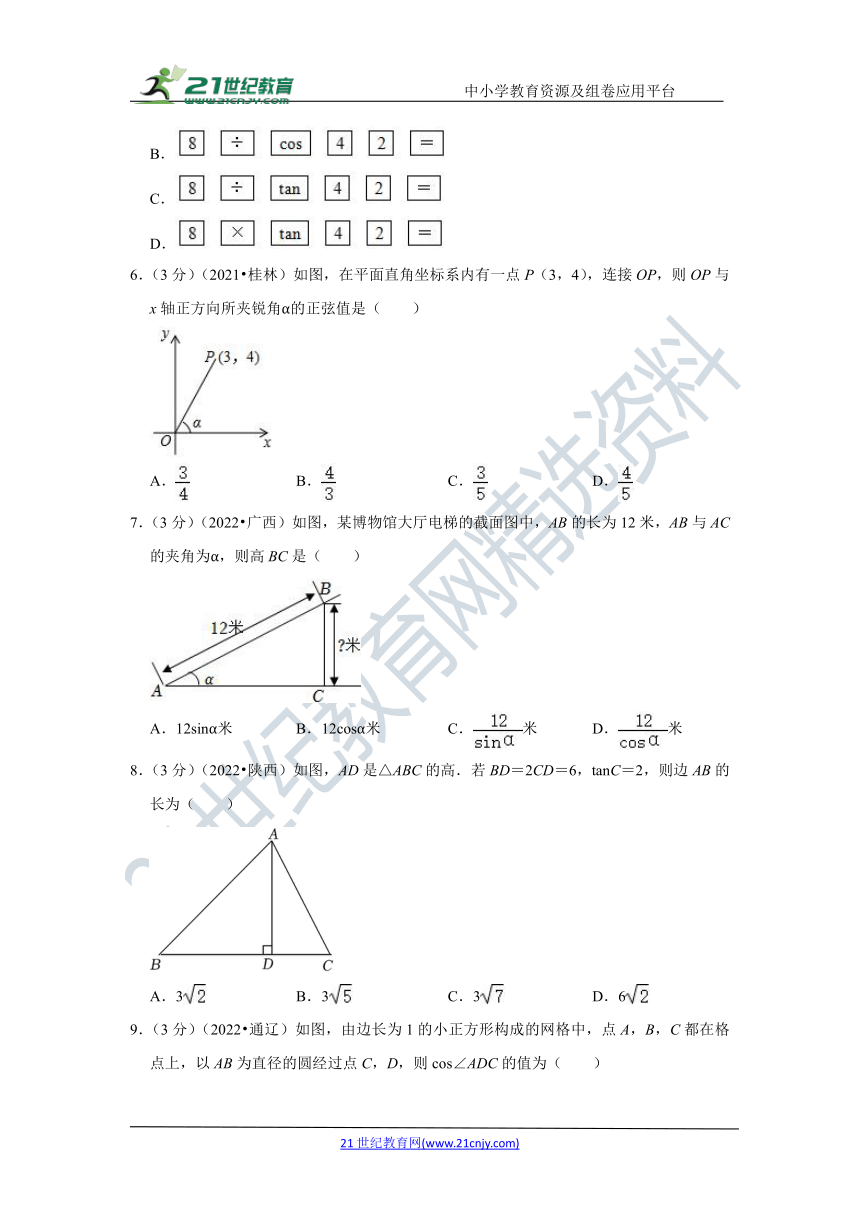
6.(3分)(2021 桂林)如图,在平面直角坐标系内有一点P(3,4),连接OP,则OP与x轴正方向所夹锐角α的正弦值是( )
A. B. C. D.
7.(3分)(2022 广西)如图,某博物馆大厅电梯的截面图中,AB的长为12米,AB与AC的夹角为α,则高BC是( )
A.12sinα米 B.12cosα米 C.米 D.米
8.(3分)(2022 陕西)如图,AD是△ABC的高.若BD=2CD=6,tanC=2,则边AB的长为( )
A.3 B.3 C.3 D.6
9.(3分)(2022 通辽)如图,由边长为1的小正方形构成的网格中,点A,B,C都在格点上,以AB为直径的圆经过点C,D,则cos∠ADC的值为( )
A. B. C. D.
10.(3分)(2022 贵港)如图,在4×4网格正方形中,每个小正方形的边长为1,顶点为格点,若△ABC的顶点均是格点,则cos∠BAC的值是( )
A. B. C. D.
11.(3分)(2022 黔东南州)如图,PA、PB分别与⊙O相切于点A、B,连接PO并延长与⊙O交于点C、D,若CD=12,PA=8,则sin∠ADB的值为( )
A. B. C. D.
12.(3分)(2022 宜宾)如图,在矩形纸片ABCD中,AB=5,BC=3,将△BCD沿BD折叠到△BED位置,DE交AB于点F,则cos∠ADF的值为( )
A. B. C. D.
13.(3分)(2022 广元)如图,在正方形方格纸中,每个小正方形的边长都相等,A、B、C、D都在格点处,AB与CD相交于点P,则cos∠APC的值为( )
A. B. C. D.
14.(3分)(2021 巴中)如图,点A、B、C在边长为1的正方形网格格点上,下列结论错误的是( )
A.sinB= B.sinC=
C.tanB= D.sin2B+sin2C=1
15.(3分)(2022 陕西)如图,AD是△ABC的高.若BD=2CD=6,tanC=2,则边AB的长为( )
A.3 B.3 C.6 D.3
16.(3分)(2021 宜宾)如图,在△ABC中,点O是角平分线AD、BE的交点,若AB=AC=10,BC=12,则tan∠OBD的值是( )
A. B.2 C. D.
17.(3分)(2022 乐山)如图,在Rt△ABC中,∠C=90°,BC=,点D是AC上一点,连结BD.若tan∠A=,tan∠ABD=,则CD的长为( )
A.2 B.3 C. D.2
18.(3分)(2022 泸州)如图,在平面直角坐标系xOy中,矩形OABC的顶点B的坐标为(10,4),四边形ABEF是菱形,且tan∠ABE=.若直线l把矩形OABC和菱形ABEF组成的图形的面积分成相等的两部分,则直线l的解析式为( )
A.y=3x B.y=﹣x+ C.y=﹣2x+11 D.y=﹣2x+12
19.(3分)(2021 黑龙江)如图,在△ABC中,∠ACB=90°,点D在AB的延长线上,连接CD,若AB=2BD,tan∠BCD=,则的值为( )
A.1 B.2 C. D.
20.(3分)(2021 淄博)如图,在Rt△ABC中,∠ACB=90°,CE是斜边AB上的中线,过点E作EF⊥AB交AC于点F.若BC=4,△AEF的面积为5,则sin∠CEF的值为( )
A. B. C. D.
21.(3分)(2022 长春)如图是长春市人民大街下穿隧道工程施工现场的一台起重机的示意图,该起重机的变幅索顶端记为点A,变幅索的底端记为点B,AD垂直地面,垂足为点D,BC⊥AD,垂足为点C.设∠ABC=α,下列关系式正确的是( )
A.sinα= B.sinα= C.sinα= D.sinα=
22.(3分)(2022 沈阳)如图,一条河的两岸互相平行,为了测量河的宽度PT(PT与河岸PQ垂直),测量得P,Q两点间距离为m米,∠PQT=α,则河宽PT的长为( )
A.msinα B.mcosα C.mtanα D.
23.(3分)(2021 十堰)如图,小明利用一个锐角是30°的三角板测操场旗杆的高度,已知他与旗杆之间的水平距离BC为15m,AB为1.5m(即小明的眼睛与地面的距离),那么旗杆的高度是( )
A.(15+)m B.5m C.15m D.(5+)m
24.(3分)(2022 黄石)我国魏晋时期的数学家刘徽首创“割圆术”:“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体,而无所失矣”,即通过圆内接正多边形割圆,从正六边形开始,每次边数成倍增加,依次可得圆内接正十二边形,内接正二十四边形,….边数越多割得越细,正多边形的周长就越接近圆的周长.再根据“圆周率等于圆周长与该圆直径的比”来计算圆周率.设圆的半径为R,图1中圆内接正六边形的周长l6=6R,则π≈=3.再利用圆的内接正十二边形来计算圆周率,则圆周率π约为( )
A.12sin15° B.12cos15° C.12sin30° D.12cos30°
25.(3分)(2022 福建)如图所示的衣架可以近似看成一个等腰三角形ABC,其中AB=AC,∠ABC=27°,BC=44cm,则高AD约为( )
(参考数据:sin27°≈0.45,cos27°≈0.89,tan27°≈0.51)
A.9.90cm B.11.22cm C.19.58cm D.22.44cm
26.(3分)(2021 长春)如图是净月潭国家森林公园一段索道的示意图.已知A、B两点间的距离为30米,∠A=α,则缆车从A点到达B点,上升的高度(BC的长)为( )
A.30sinα米 B.米 C.30cosα米 D.米
27.(3分)(2022 金华)一配电房示意图如图所示,它是一个轴对称图形.已知BC=6m,∠ABC=α,则房顶A离地面EF的高度为( )
A.(4+3sinα)m B.(4+3tanα)m C.(4+)m D.(4+)m
28.(3分)(2021 呼和浩特)如图,正方形的边长为4,剪去四个角后成为一个正八边形,则可求出此正八边形的外接圆直径d,根据我国魏晋时期数学家刘徽的“割圆术”思想,如果用此正八边形的周长近似代替其外接圆周长,便可估计π的值,下面d及π的值都正确的是( )
A.d=,π≈8sin22.5°
B.d=,π≈4sin22.5°
C.d=,π≈8sin22.5°
D.d=,π≈4sin22.5°
29.(3分)(2022 毕节市)如图,某地修建的一座建筑物的截面图的高BC=5m,坡面AB的坡度为1:,则AB的长度为( )
A.10m B.10m C.5m D.5m
30.(3分)(2022 黑龙江)小明去爬山,在山脚看山顶角度为30°,小明在坡比为5:12的山坡上走1300米,此时小明看山顶的角度为60°,山高为( )米
A.600﹣250 B.600﹣250 C.350+350 D.500
31.(3分)(2022 十堰)如图,坡角为α的斜坡上有一棵垂直于水平地面的大树AB,当太阳光线与水平线成45°角沿斜坡照下时,在斜坡上的树影BC长为m,则大树AB的高为( )
A.m(cosα﹣sinα) B.m(sinα﹣cosα)
C.m(cosα﹣tanα) D.﹣
32.(3分)(2021 德州)某商场准备改善原有楼梯的安全性能,把坡角由37°减至30°,已知原楼梯长为5米,调整后的楼梯会加长( )(参考数据:sin37°≈,cos37°≈,tan37°≈).
A.6米 B.3米 C.2米 D.1米
33.(3分)(2021 潍坊)如图,一束水平光线照在有一定倾斜角度的平面镜上,若入射光线与出射光线的夹角为60°,则平面镜的垂线与水平地面的夹角α的度数是( )
A.15° B.30° C.45° D.60°
34.(3分)(2022 随州)如图,已知点B,D,C在同一直线的水平地面上,在点C处测得建筑物AB的顶端A的仰角为α,在点D处测得建筑物AB的顶端A的仰角为β,若CD=α,则建筑物AB的高度为( )
A. B.
C. D.
35.(3分)(2021 济南)无人机低空遥感技术已广泛应用于农作物监测.如图,某农业特色品牌示范基地用无人机对一块试验田进行监测作业时,在距地面高度为135m的A处测得试验田右侧边界N处俯角为43°,无人机垂直下降40m至B处,又测得试验田左侧边界M处俯角为35°,则M,N之间的距离为( )(参考数据:tan43°≈0.9,sin43°≈0.7,cos35°≈0.8,tan35°≈0.7,结果保留整数)
A.188m B.269m C.286m D.312m
36.(3分)(2022 济南)数学活动小组到某广场测量标志性建筑AB的高度.如图,他们在地面上C点测得最高点A的仰角为22°,再向前70m至D点,又测得最高点A的仰角为58°,点C,D,B在同一直线上,则该建筑物AB的高度约为( )
(精确到1m.参考数据:sin22°≈0.37,tan22°≈0.40,sin58°≈0.85,tan58°≈1.60)
A.28m B.34m C.37m D.46m
37.(3分)(2022 贵港)如图,某数学兴趣小组测量一棵树CD的高度,在点A处测得树顶C的仰角为45°,在点B处测得树顶C的仰角为60°,且A,B,D三点在同一直线上,若AB=16m,则这棵树CD的高度是( )
A.8(3﹣)m B.8(3+)m C.6(3﹣)m D.6(3+)m
38.(3分)(2022 玉林)如图,从热气球A看一栋楼底部C的俯角是( )
A.∠BAD B.∠ACB C.∠BAC D.∠DAC
39.(3分)(2021 日照)如图,在一次数学实践活动中,小明同学要测量一座与地面垂直的古塔AB的高度,他从古塔底部点B处前行30m到达斜坡CE的底部点C处,然后沿斜坡CE前行20m到达最佳测量点D处,在点D处测得塔顶A的仰角为30°,已知斜坡的斜面坡度i=1:,且点A,B,C,D,E在同一平面内,小明同学测得古塔AB的高度是( )
A.(10+20)m B.(10+10)m C.20m D.40m
40.(3分)(2021 深圳)如图,在点F处,看建筑物顶端D的仰角为32°,向前走了15米到达点E即EF=15米,在点E处看点D的仰角为64°,则CD的长用三角函数表示为( )
A.15sin32° B.15tan64° C.15sin64° D.15tan32°
【真题汇编】2023年中考数学备考之锐角三角函数(选择题40题)
参考答案与试题解析
一.选择题(共40小题,满分120分,每小题3分)
1.(3分)(2022 荆州)如图,在平面直角坐标系中,点A,B分别在x轴负半轴和y轴正半轴上,点C在OB上,OC:BC=1:2,连接AC,过点O作OP∥AB交AC的延长线于P.若P(1,1),则tan∠OAP的值是( )
A. B. C. D.3
【解析】解:如图,过点P作PQ⊥x轴于点Q,
∵OP∥AB,
∴△OCP∽△BCA,
∴CP:AC=OC:BC=1:2,
∵∠AOC=∠AQP=90°,
∴CO∥PQ,
∴OQ:AO=CP:AC=1:2,
∵P(1,1),
∴PQ=OQ=1,
∴AO=2,
∴tan∠OAP===.
故选:C.
2.(3分)(2022 天津)tan45°的值等于( )
A.2 B.1 C. D.
【解析】解:tan45°的值等于1,
故选:B.
3.(3分)(2021 烟台)如图所示,若用我们数学课本上采用的科学计算器进行计算,其按键顺序及结果如下:
按键的结果为m;
按键的结果为n;
按键的结果为k.
下列判断正确的是( )
A.m=n B.n=k C.m=k D.m=n=k
【解析】解:m=23﹣=8﹣4=4;
n=﹣22=4﹣4=0;
k=﹣cos60°=﹣=4;
∴m=k,
故选:C.
4.(3分)(2021 威海)若用我们数学课本上采用的科学计算器计算sin36°18′,按键顺序正确的是( )
A.
B.
C.
D.
【解析】解:采用的科学计算器计算sin36°18′,按键顺序正确的是D选项中的顺序,
故选:D.
5.(3分)(2021 东营)如图,在△ABC中,∠C=90°,∠B=42°,BC=8,若用科学计算器求AC的长,则下列按键顺序正确的是( )
A.
B.
C.
D.
【解析】解:在△ABC中,因为∠C=90°,
所以tanB=,
因为∠B=42°,BC=8,
所以AC=BC tanB=8×tan42°.
故选:D.
6.(3分)(2021 桂林)如图,在平面直角坐标系内有一点P(3,4),连接OP,则OP与x轴正方向所夹锐角α的正弦值是( )
A. B. C. D.
【解析】解:作PA⊥x轴于A,如右图.
∵P(3,4),
∴OA=3,AP=4,
∴OP==5,
∴sinα=.
故选:D.
7.(3分)(2022 广西)如图,某博物馆大厅电梯的截面图中,AB的长为12米,AB与AC的夹角为α,则高BC是( )
A.12sinα米 B.12cosα米 C.米 D.米
【解析】解:Rt△ABC中,sinα=,
∵AB=12米,
∴BC=12sinα(米).
故选:A.
8.(3分)(2022 陕西)如图,AD是△ABC的高.若BD=2CD=6,tanC=2,则边AB的长为( )
A.3 B.3 C.3 D.6
【解析】解:∵2CD=6,
∴CD=3,
∵tanC=2,
∴=2,
∴AD=6,
在Rt△ABD中,由勾股定理得,
AB=,
故选:D.
9.(3分)(2022 通辽)如图,由边长为1的小正方形构成的网格中,点A,B,C都在格点上,以AB为直径的圆经过点C,D,则cos∠ADC的值为( )
A. B. C. D.
【解析】解:∵AB为直径,
∴∠ACB=90°,
又∵点A,B,C都在格点上,
∴∠ADC=∠ABC,
在Rt△ABC中,
cos∠ABC====cos∠ADC,
故选:B.
10.(3分)(2022 贵港)如图,在4×4网格正方形中,每个小正方形的边长为1,顶点为格点,若△ABC的顶点均是格点,则cos∠BAC的值是( )
A. B. C. D.
【解析】解:延长AC到D,连接BD,如图:
∵AD2=20,BD2=5,AB2=25,
∴AD2+BD2=AB2,
∴∠ADB=90°,
∴cos∠BAC===,
故选:C.
11.(3分)(2022 黔东南州)如图,PA、PB分别与⊙O相切于点A、B,连接PO并延长与⊙O交于点C、D,若CD=12,PA=8,则sin∠ADB的值为( )
A. B. C. D.
【解析】解连接AO,BO,
∵PA、PB分别与⊙O相切于点A、B,
∴∠PAO=∠PBO=90°,PA=PB=8,
∵DC=12,
∴AO=6,
∴OP=10,
在Rt△PAO和Rt△PBO中,
,
∴Rt△PAO≌Rt△PBO(HL),
∴∠AOP=∠BOP,
∴,
∴∠ADC=∠BDC,
∵∠AOC=2∠ADC,
∴∠ADB=∠AOC,
∴sin∠ADB=sin∠AOC==.
故选:A.
12.(3分)(2022 宜宾)如图,在矩形纸片ABCD中,AB=5,BC=3,将△BCD沿BD折叠到△BED位置,DE交AB于点F,则cos∠ADF的值为( )
A. B. C. D.
【解析】解:∵四边形ABCD是矩形,
∴∠A=90°,AB∥CD,AD=BC=3,AB=CD=5,
∴∠BDC=∠DBF,
由折叠的性质可得∠BDC=∠BDF,
∴∠BDF=∠DBF,
∴BF=DF,
设BF=x,则DF=x,AF=5﹣x,
在Rt△ADF中,32+(5﹣x)2=x2,
∴x=,
∴cos∠ADF=,
故选:C.
13.(3分)(2022 广元)如图,在正方形方格纸中,每个小正方形的边长都相等,A、B、C、D都在格点处,AB与CD相交于点P,则cos∠APC的值为( )
A. B. C. D.
【解析】解:把AB向上平移一个单位到DE,连接CE,如图.
则DE∥AB,
∴∠APC=∠EDC.
在△DCE中,有EC==,DC==2,DE==5,
∵EC2+DC2=DE2,
故△DCE为直角三角形,∠DCE=90°.
∴cos∠APC=cos∠EDC==.
故选:B.
14.(3分)(2021 巴中)如图,点A、B、C在边长为1的正方形网格格点上,下列结论错误的是( )
A.sinB= B.sinC=
C.tanB= D.sin2B+sin2C=1
【解析】解:由勾股定理得:AB=,AC=,BC=,
∴BC2=AB2+AC2,
∴△ABC是直角三角形,∠BAC=90°,
∴sinB=,sinC=,tanB=,sin2B+sin2C=,
故选:A.
15.(3分)(2022 陕西)如图,AD是△ABC的高.若BD=2CD=6,tanC=2,则边AB的长为( )
A.3 B.3 C.6 D.3
【解析】解:∵BD=2CD=6,
∴CD=3,BD=6,
∵tanC==2,
∴AD=6,
∴AB=AD=6
故选:C.
16.(3分)(2021 宜宾)如图,在△ABC中,点O是角平分线AD、BE的交点,若AB=AC=10,BC=12,则tan∠OBD的值是( )
A. B.2 C. D.
【解析】解:如图:
作OF⊥AB于F,
∵AB=AC,AD平分∠BAC.
∴∠ODB=90°.BD=CD=6.
∴根据勾股定理得:AD==8.
∵BE平分∠ABC.
∴OF=OD,BF=BD=6,AF=10﹣6=4.
设OD=OF=x,则AO=8﹣x,在Rt△AOF中,根据勾股定理得:
(8﹣x)2=x2+42.
∴x=3.
∴OD=3.
在Rt△OBD中,tan∠OBD===.
法二:在求出AF=4后
∵tan∠BAD==.
∴=.
∴OF=3.
∴OD=OF=3.
∴tan∠OBD==.
故选:A.
17.(3分)(2022 乐山)如图,在Rt△ABC中,∠C=90°,BC=,点D是AC上一点,连结BD.若tan∠A=,tan∠ABD=,则CD的长为( )
A.2 B.3 C. D.2
【解析】解:过D点作DE⊥AB于E,
∵tan∠A==,tan∠ABD==,
∴AE=2DE,BE=3DE,
∴2DE+3DE=5DE=AB,
在Rt△ABC中,tan∠A=,BC=,
∴,
解得AC=,
∴AB=,
∴DE=1,
∴AE=2,
∴AD=,
∴CD=AC﹣AD=,
故选:C.
18.(3分)(2022 泸州)如图,在平面直角坐标系xOy中,矩形OABC的顶点B的坐标为(10,4),四边形ABEF是菱形,且tan∠ABE=.若直线l把矩形OABC和菱形ABEF组成的图形的面积分成相等的两部分,则直线l的解析式为( )
A.y=3x B.y=﹣x+ C.y=﹣2x+11 D.y=﹣2x+12
【解析】解:连接OB,AC,它们交于点M,连接AE,BF,它们交于点N,
则直线MN为符合条件的直线l,如图,
∵四边形OABC是矩形,
∴OM=BM.
∵B的坐标为(10,4),
∴M(5,2),AB=10,BC=4.
∵四边形ABEF为菱形,
BE=AB=10.
过点E作EG⊥AB于点G,
在Rt△BEG中,
∵tan∠ABE=,
∴,
设EG=4k,则BG=3k,
∴BE==5k,
∴5k=10,
∴k=2,
∴EG=8,BG=6,
∴AG=4.
∴E(4,12).
∵B的坐标为(10,4),AB∥x轴,
∴A(0,4).
∵点N为AE的中点,
∴N(2,8).
设直线l的解析式为y=ax+b,
∴,
解得:,
∴直线l的解析式为y=﹣2x+12,
故选:D.
19.(3分)(2021 黑龙江)如图,在△ABC中,∠ACB=90°,点D在AB的延长线上,连接CD,若AB=2BD,tan∠BCD=,则的值为( )
A.1 B.2 C. D.
【解析】解:过点D作DM⊥BC,交CB的延长线于点M,
∵∠ACB=∠DMB=90°,∠ABC=∠DBM,
∴△ABC∽△DBM,
∴==,
∵AB=2BD,
∴===,
在Rt△CDM中,
由于tan∠MCD==,设DM=2k,则CM=3k,
又∵==,
∴BC=2k,AC=4k,
∴==2,
故选:B.
20.(3分)(2021 淄博)如图,在Rt△ABC中,∠ACB=90°,CE是斜边AB上的中线,过点E作EF⊥AB交AC于点F.若BC=4,△AEF的面积为5,则sin∠CEF的值为( )
A. B. C. D.
【解析】解:连接BF,
∵CE是斜边AB上的中线,EF⊥AB,
∴EF是AB的垂直平分线,
∴S△AFE=S△BFE=5,∠FBA=∠A,
∴S△AFB=10=AF BC,
∵BC=4,
∴AF=5=BF,
在Rt△BCF中,BC=4,BF=5,
∴CF==3,
∵CE=AE=BE=AB,
∴∠A=∠FBA=∠ACE,
又∵∠BCA=90°=∠BEF,
∴∠CBF=90°﹣∠BFC=90°﹣2∠A,
∠CEF=90°﹣∠BEC=90°﹣2∠A,
∴∠CEF=∠FBC,
∴sin∠CEF=sin∠FBC==,
故选:A.
21.(3分)(2022 长春)如图是长春市人民大街下穿隧道工程施工现场的一台起重机的示意图,该起重机的变幅索顶端记为点A,变幅索的底端记为点B,AD垂直地面,垂足为点D,BC⊥AD,垂足为点C.设∠ABC=α,下列关系式正确的是( )
A.sinα= B.sinα= C.sinα= D.sinα=
【解析】解:在Rt△ABC中,∠ACB=90°,∠ABC=α,由锐角三角函数的定义可知,
sinα=sin∠ABC=,
故选:D.
22.(3分)(2022 沈阳)如图,一条河的两岸互相平行,为了测量河的宽度PT(PT与河岸PQ垂直),测量得P,Q两点间距离为m米,∠PQT=α,则河宽PT的长为( )
A.msinα B.mcosα C.mtanα D.
【解析】解:由题意得:
PT⊥PQ,
∴∠APQ=90°,
在Rt△APQ中,PQ=m米,∠PQT=α,
∴PT=PQ tanα=mtanα(米),
∴河宽PT的长度是mtanα米,
故选:C.
23.(3分)(2021 十堰)如图,小明利用一个锐角是30°的三角板测操场旗杆的高度,已知他与旗杆之间的水平距离BC为15m,AB为1.5m(即小明的眼睛与地面的距离),那么旗杆的高度是( )
A.(15+)m B.5m C.15m D.(5+)m
【解析】解:由题意可得,四边形ABCD是矩形,BC=15m,AB=1.5m,
∴BC=AD=15m,AB=CD=1.5m,
在Rt△ADE中,∠EAD=30°,AD=15m,
∴DE=AD tan∠EAD=15×=5(m),
∴CE=CD+DE=(5+1.5)(m).
故选:D.
24.(3分)(2022 黄石)我国魏晋时期的数学家刘徽首创“割圆术”:“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体,而无所失矣”,即通过圆内接正多边形割圆,从正六边形开始,每次边数成倍增加,依次可得圆内接正十二边形,内接正二十四边形,….边数越多割得越细,正多边形的周长就越接近圆的周长.再根据“圆周率等于圆周长与该圆直径的比”来计算圆周率.设圆的半径为R,图1中圆内接正六边形的周长l6=6R,则π≈=3.再利用圆的内接正十二边形来计算圆周率,则圆周率π约为( )
A.12sin15° B.12cos15° C.12sin30° D.12cos30°
【解析】解:在正十二边形中,∠A6OM=360°÷24=15°,
∴A6M=sin15°×OA6=R×sin15°,
∵OA6=OA7,OM⊥A6A7,
∴A6A7=2A6M=2R×sin15°,
∴π≈=12sin15°,
故选:A.
25.(3分)(2022 福建)如图所示的衣架可以近似看成一个等腰三角形ABC,其中AB=AC,∠ABC=27°,BC=44cm,则高AD约为( )
(参考数据:sin27°≈0.45,cos27°≈0.89,tan27°≈0.51)
A.9.90cm B.11.22cm C.19.58cm D.22.44cm
【解析】解:∵AB=AC,BC=44cm,
∴BD=CD=22cm,AD⊥BC,
∵∠ABC=27°,
∴tan∠ABC=≈0.51,
∴AD≈0.51×22=11.22cm,
故选:B.
26.(3分)(2021 长春)如图是净月潭国家森林公园一段索道的示意图.已知A、B两点间的距离为30米,∠A=α,则缆车从A点到达B点,上升的高度(BC的长)为( )
A.30sinα米 B.米 C.30cosα米 D.米
【解析】解:由图可知,在△ABC中,AC⊥BC,
∴sinα==,
∴BC=30sinα米.
故选:A.
27.(3分)(2022 金华)一配电房示意图如图所示,它是一个轴对称图形.已知BC=6m,∠ABC=α,则房顶A离地面EF的高度为( )
A.(4+3sinα)m B.(4+3tanα)m C.(4+)m D.(4+)m
【解析】解:过点A作AD⊥BC于点D,如图,
∵它是一个轴对称图形,
∴AB=AC,
∵AD⊥BC,
∴BD=BC=3m,
在Rt△ADB中,
∵tan∠ABC=,
∴AD=BD tanα=3tanαm.
∴房顶A离地面EF的高度=AD+BE=(4+3tanα)m,
故选:B.
28.(3分)(2021 呼和浩特)如图,正方形的边长为4,剪去四个角后成为一个正八边形,则可求出此正八边形的外接圆直径d,根据我国魏晋时期数学家刘徽的“割圆术”思想,如果用此正八边形的周长近似代替其外接圆周长,便可估计π的值,下面d及π的值都正确的是( )
A.d=,π≈8sin22.5°
B.d=,π≈4sin22.5°
C.d=,π≈8sin22.5°
D.d=,π≈4sin22.5°
【解析】解:如图,连接AD,BC交于点O,过点O作OP⊥BC于点P,
则CP=PD,且∠COP=22.5°,
设正八边形的边长为a,则a+2×a=4,
解得a=4(﹣1),
在Rt△OCP中,OC==,
∴d=2OC=,
由πd≈8CD,
则π≈32(﹣1),
∴π≈8sin22.5°.
故选:C.
29.(3分)(2022 毕节市)如图,某地修建的一座建筑物的截面图的高BC=5m,坡面AB的坡度为1:,则AB的长度为( )
A.10m B.10m C.5m D.5m
【解析】解:∵坡面AB的坡度为==1:,
∴AC=5m,
∴AB==10m.
故选:A.
30.(3分)(2022 黑龙江)小明去爬山,在山脚看山顶角度为30°,小明在坡比为5:12的山坡上走1300米,此时小明看山顶的角度为60°,山高为( )米
A.600﹣250 B.600﹣250 C.350+350 D.500
【解析】解:设EF=5x米,
∵斜坡BE的坡度为5:12,
∴BF=12x米,
由勾股定理得:(5x)2+(12x)2=(1300)2,
解得:x=100,
则EF=500米,BF=1200米,
由题意可知,四边形DCFE为矩形,
∴DC=EF=500米,DE=CF,
在Rt△ADE中,tan∠AED=,
则DE==AD,
在Rt△ACB中,tan∠ABC=,
∴=,
解得:AD=600﹣750,
∴山高AC=AD+DC=600﹣750+500=(600﹣250)米,
故选:B.
31.(3分)(2022 十堰)如图,坡角为α的斜坡上有一棵垂直于水平地面的大树AB,当太阳光线与水平线成45°角沿斜坡照下时,在斜坡上的树影BC长为m,则大树AB的高为( )
A.m(cosα﹣sinα) B.m(sinα﹣cosα)
C.m(cosα﹣tanα) D.﹣
【解析】解:过点C作水平地面的平行线,交AB的延长线于D,
则∠BCD=α,
在Rt△BCD中,BC=m,∠BCD=α,
则BD=BC sin∠BCD=msinα,CD=BC cos∠BCD=mcosα,
在Rt△ACD中,∠ACD=45°,
则AD=CD=mcosα,
∴AB=AD﹣BD=mcosα﹣msinα=m(cosα﹣sinα),
故选:A.
32.(3分)(2021 德州)某商场准备改善原有楼梯的安全性能,把坡角由37°减至30°,已知原楼梯长为5米,调整后的楼梯会加长( )(参考数据:sin37°≈,cos37°≈,tan37°≈).
A.6米 B.3米 C.2米 D.1米
【解析】解:在Rt△BAD中,AB=5米,∠BAD=37°,
则BD=AB sin∠BAD≈5×=3(米),
在Rt△BCD中,∠C=30°,
∴BC=2BD=6(米),
则调整后的楼梯会加长:6﹣5=1(米),
故选:D.
33.(3分)(2021 潍坊)如图,一束水平光线照在有一定倾斜角度的平面镜上,若入射光线与出射光线的夹角为60°,则平面镜的垂线与水平地面的夹角α的度数是( )
A.15° B.30° C.45° D.60°
【解析】解:如图,作CD⊥平面镜,垂足为G,交地面于D.
∵EF⊥平面镜,
∴CD∥EF,
∴∠CDH=∠EFH=α,
根据题意可知:AG∥DF,
∴∠AGC=∠CDH=α,
∴∠AGC=α,
∵∠AGC=AGB=×60°=30°,
∴α=30°.
故选:B.
34.(3分)(2022 随州)如图,已知点B,D,C在同一直线的水平地面上,在点C处测得建筑物AB的顶端A的仰角为α,在点D处测得建筑物AB的顶端A的仰角为β,若CD=α,则建筑物AB的高度为( )
A. B.
C. D.
【解析】解:设AB=x,
在Rt△ABD中,tanβ=,
∴BD=,
∴BC=BD+CD=a+,
在Rt△ABC中,tanα=,
解得x=.
故选:D.
35.(3分)(2021 济南)无人机低空遥感技术已广泛应用于农作物监测.如图,某农业特色品牌示范基地用无人机对一块试验田进行监测作业时,在距地面高度为135m的A处测得试验田右侧边界N处俯角为43°,无人机垂直下降40m至B处,又测得试验田左侧边界M处俯角为35°,则M,N之间的距离为( )(参考数据:tan43°≈0.9,sin43°≈0.7,cos35°≈0.8,tan35°≈0.7,结果保留整数)
A.188m B.269m C.286m D.312m
【解析】解:由题意得:∠N=43°,∠M=35°,AO=135m,BO=AO﹣AB=95m,
在Rt△AON中,
tanN==tan43°,
∴NO=≈150m,
在Rt△BOM中,
tanM==tan35°,
∴MO=≈135.7m,
∴MN=MO+NO=135.7+150≈286m.
故选:C.
36.(3分)(2022 济南)数学活动小组到某广场测量标志性建筑AB的高度.如图,他们在地面上C点测得最高点A的仰角为22°,再向前70m至D点,又测得最高点A的仰角为58°,点C,D,B在同一直线上,则该建筑物AB的高度约为( )
(精确到1m.参考数据:sin22°≈0.37,tan22°≈0.40,sin58°≈0.85,tan58°≈1.60)
A.28m B.34m C.37m D.46m
【解析】解:由题意可知:AB⊥BC,
在Rt△ADB中,∠B=90°,∠ADB=58°,
∵tan∠ADB=tan58°=,
∴BD=≈(m),
在Rt△ACB中,∠B=90°,∠C=22°,
∵CD=70m,
∴BC=CD+BD=(70+)m,
∴AB=BC×tanC≈(70+)×0.40(m),
解得:AB≈37m,
答:该建筑物AB的高度约为37m.
故选:C.
37.(3分)(2022 贵港)如图,某数学兴趣小组测量一棵树CD的高度,在点A处测得树顶C的仰角为45°,在点B处测得树顶C的仰角为60°,且A,B,D三点在同一直线上,若AB=16m,则这棵树CD的高度是( )
A.8(3﹣)m B.8(3+)m C.6(3﹣)m D.6(3+)m
【解析】解:设AD=x米,
∵AB=16米,
∴BD=AB﹣AD=(16﹣x)米,
在Rt△ADC中,∠A=45°,
∴CD=AD tan45°=x(米),
在Rt△CDB中,∠B=60°,
∴tan60°===,
∴x=24﹣8,
经检验:x=24﹣8是原方程的根,
∴CD=24﹣8=8(3﹣))米,
∴这棵树CD的高度是8(3﹣)米,
故选:A.
38.(3分)(2022 玉林)如图,从热气球A看一栋楼底部C的俯角是( )
A.∠BAD B.∠ACB C.∠BAC D.∠DAC
【解析】解:从热气球A看一栋楼底部C的俯角是∠DAC.
故选:D.
39.(3分)(2021 日照)如图,在一次数学实践活动中,小明同学要测量一座与地面垂直的古塔AB的高度,他从古塔底部点B处前行30m到达斜坡CE的底部点C处,然后沿斜坡CE前行20m到达最佳测量点D处,在点D处测得塔顶A的仰角为30°,已知斜坡的斜面坡度i=1:,且点A,B,C,D,E在同一平面内,小明同学测得古塔AB的高度是( )
A.(10+20)m B.(10+10)m C.20m D.40m
【解析】解:过D作DF⊥BC于F,DH⊥AB于H,
∴DH=BF,BH=DF,
∵斜坡的斜面坡度i=1:,
∴=1:,
设DF=xm,CF=xm,
∴CD==2xm=20m,
∴x=10,
∴BH=DF=10m,CF=10m,
∴DH=BF=(10+30)m,
∵∠ADH=30°,
∴AH=DH=×(10+30)=(10+10)m,
∴AB=AH+BH=(20+10)m,
故选:A.
40.(3分)(2021 深圳)如图,在点F处,看建筑物顶端D的仰角为32°,向前走了15米到达点E即EF=15米,在点E处看点D的仰角为64°,则CD的长用三角函数表示为( )
A.15sin32° B.15tan64° C.15sin64° D.15tan32°
【解析】解:∵∠CED=64°,∠F=32°,∠CED=∠F+∠EDF,
∴∠EDF=∠CED﹣∠F=64°﹣32°=32°,
∴∠EDF=∠F,
∴DE=EF,
∵EF=15米,
∴DE=15米,
在Rt△CDE中,
∵sin∠CED=,
∴CD=DEsin∠CED=15sin64°,
故选:C.
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
【真题汇编】2023年中考数学备考之锐角三角函数
1.锐角三角函数的定义
在Rt△ABC中,∠C=90°.
(1)正弦:我们把锐角A的对边a与斜边c的比叫做∠A的正弦,记作sinA.
即sinA=∠A的对边除以斜边=.
(2)余弦:锐角A的邻边b与斜边c的比叫做∠A的余弦,记作cosA.
即cosA=∠A的邻边除以斜边=.
(3)正切:锐角A的对边a与邻边b的比叫做∠A的正切,记作tanA.
即tanA=∠A的对边除以∠A的邻边=.
(4)三角函数:锐角A的正弦、余弦、正切都叫做∠A的锐角三角函数.
2.特殊角的三角函数值
(1)特指30°、45°、60°角的各种三角函数值.
sin30°=; cos30°=;tan30°=;
sin45°=;cos45°=;tan45°=1;
sin60°=;cos60°=; tan60°=;
(2)应用中要熟记特殊角的三角函数值,一是按值的变化规律去记,正弦逐渐增大,余弦逐渐减小,正切逐渐增大;二是按特殊直角三角形中各边特殊值规律去记.
(3)特殊角的三角函数值应用广泛,一是它可以当作数进行运算,二是具有三角函数的特点,在解直角三角形中应用较多.
3.计算器—三角函数
(1)用计算器可以求出任意锐角的三角函数值,也可以根据三角函数值求出锐角的度数.
(2)求锐角三角函数值的方法:
如求tan46°35′的值时,先按键“tan”,再输入角的度数46°35′,按键“=”即可得到结果.
注意:不同型号的计算器使用方法不同.
(3)已知锐角三角函数值求锐角的方法是:
如已知sinα=0.5678,一般先按键“2ndF”,再按键“sin”,输入“0.5678”,再按键“=”即可得到结果.
注意:一般情况下,三角函数值直接可以求出,已知三角函数值求角需要用第二功能键.
4.解直角三角形
(1)解直角三角形的定义
在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.
(2)解直角三角形要用到的关系
①锐角、直角之间的关系:∠A+∠B=90°;
②三边之间的关系:a2+b2=c2;
③边角之间的关系:
sinA==,cosA==,tanA==.
(a,b,c分别是∠A、∠B、∠C的对边)
5.解直角三角形的应用
(1)通过解直角三角形能解决实际问题中的很多有关测量问.
如:测不易直接测量的物体的高度、测河宽等,关键在于构造出直角三角形,通过测量角的度数和测量边的长度,计算出所要求的物体的高度或长度.
(2)解直角三角形的一般过程是:
①将实际问题抽象为数学问题(画出平面图形,构造出直角三角形转化为解直角三角形问题).
②根据题目已知特点选用适当锐角三角函数或边角关系去解直角三角形,得到数学问题的答案,再转化得到实际问题的答案.
6.解直角三角形的应用-坡度坡角问题
(1)坡度是坡面的铅直高度h和水平宽度l的比,又叫做坡比,它是一个比值,反映了斜坡的陡峭程度,一般用i表示,常写成i=1:m的形式.
(2)把坡面与水平面的夹角α叫做坡角,坡度i与坡角α之间的关系为:i=h/l=tanα.
(3)在解决坡度的有关问题中,一般通过作高构成直角三角形,坡角即是一锐角,坡度实际就是一锐角的正切值,水平宽度或铅直高度都是直角边,实质也是解直角三角形问题.
应用领域:①测量领域;②航空领域 ③航海领域:④工程领域等.
7.解直角三角形的应用-仰角俯角问题
(1)概念:仰角是向上看的视线与水平线的夹角;俯角是向下看的视线与水平线的夹角.
(2)解决此类问题要了解角之间的关系,找到与已知和未知相关联的直角三角形,当图形中没有直角三角形时,要通过作高或垂线构造直角三角形,另当问题以一个实际问题的形式给出时,要善于读懂题意,把实际问题划归为直角三角形中边角关系问题加以解决.
【真题汇编】2023年中考数学备考之锐角三角函数
(选择题40题)
满分:120分 建议时间:100分钟
学校:___________姓名:___________班级:___________考号:___________
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息2.请将答案正确填写在答题卡上
一.选择题(共40小题,满分120分,每小题3分)
1.(3分)(2022 荆州)如图,在平面直角坐标系中,点A,B分别在x轴负半轴和y轴正半轴上,点C在OB上,OC:BC=1:2,连接AC,过点O作OP∥AB交AC的延长线于P.若P(1,1),则tan∠OAP的值是( )
A. B. C. D.3
2.(3分)(2022 天津)tan45°的值等于( )
A.2 B.1 C. D.
3.(3分)(2021 烟台)如图所示,若用我们数学课本上采用的科学计算器进行计算,其按键顺序及结果如下:
按键的结果为m;
按键的结果为n;
按键的结果为k.
下列判断正确的是( )
A.m=n B.n=k C.m=k D.m=n=k
4.(3分)(2021 威海)若用我们数学课本上采用的科学计算器计算sin36°18′,按键顺序正确的是( )
A.
B.
C.
D.
5.(3分)(2021 东营)如图,在△ABC中,∠C=90°,∠B=42°,BC=8,若用科学计算器求AC的长,则下列按键顺序正确的是( )
A.
B.
C.
D.
6.(3分)(2021 桂林)如图,在平面直角坐标系内有一点P(3,4),连接OP,则OP与x轴正方向所夹锐角α的正弦值是( )
A. B. C. D.
7.(3分)(2022 广西)如图,某博物馆大厅电梯的截面图中,AB的长为12米,AB与AC的夹角为α,则高BC是( )
A.12sinα米 B.12cosα米 C.米 D.米
8.(3分)(2022 陕西)如图,AD是△ABC的高.若BD=2CD=6,tanC=2,则边AB的长为( )
A.3 B.3 C.3 D.6
9.(3分)(2022 通辽)如图,由边长为1的小正方形构成的网格中,点A,B,C都在格点上,以AB为直径的圆经过点C,D,则cos∠ADC的值为( )
A. B. C. D.
10.(3分)(2022 贵港)如图,在4×4网格正方形中,每个小正方形的边长为1,顶点为格点,若△ABC的顶点均是格点,则cos∠BAC的值是( )
A. B. C. D.
11.(3分)(2022 黔东南州)如图,PA、PB分别与⊙O相切于点A、B,连接PO并延长与⊙O交于点C、D,若CD=12,PA=8,则sin∠ADB的值为( )
A. B. C. D.
12.(3分)(2022 宜宾)如图,在矩形纸片ABCD中,AB=5,BC=3,将△BCD沿BD折叠到△BED位置,DE交AB于点F,则cos∠ADF的值为( )
A. B. C. D.
13.(3分)(2022 广元)如图,在正方形方格纸中,每个小正方形的边长都相等,A、B、C、D都在格点处,AB与CD相交于点P,则cos∠APC的值为( )
A. B. C. D.
14.(3分)(2021 巴中)如图,点A、B、C在边长为1的正方形网格格点上,下列结论错误的是( )
A.sinB= B.sinC=
C.tanB= D.sin2B+sin2C=1
15.(3分)(2022 陕西)如图,AD是△ABC的高.若BD=2CD=6,tanC=2,则边AB的长为( )
A.3 B.3 C.6 D.3
16.(3分)(2021 宜宾)如图,在△ABC中,点O是角平分线AD、BE的交点,若AB=AC=10,BC=12,则tan∠OBD的值是( )
A. B.2 C. D.
17.(3分)(2022 乐山)如图,在Rt△ABC中,∠C=90°,BC=,点D是AC上一点,连结BD.若tan∠A=,tan∠ABD=,则CD的长为( )
A.2 B.3 C. D.2
18.(3分)(2022 泸州)如图,在平面直角坐标系xOy中,矩形OABC的顶点B的坐标为(10,4),四边形ABEF是菱形,且tan∠ABE=.若直线l把矩形OABC和菱形ABEF组成的图形的面积分成相等的两部分,则直线l的解析式为( )
A.y=3x B.y=﹣x+ C.y=﹣2x+11 D.y=﹣2x+12
19.(3分)(2021 黑龙江)如图,在△ABC中,∠ACB=90°,点D在AB的延长线上,连接CD,若AB=2BD,tan∠BCD=,则的值为( )
A.1 B.2 C. D.
20.(3分)(2021 淄博)如图,在Rt△ABC中,∠ACB=90°,CE是斜边AB上的中线,过点E作EF⊥AB交AC于点F.若BC=4,△AEF的面积为5,则sin∠CEF的值为( )
A. B. C. D.
21.(3分)(2022 长春)如图是长春市人民大街下穿隧道工程施工现场的一台起重机的示意图,该起重机的变幅索顶端记为点A,变幅索的底端记为点B,AD垂直地面,垂足为点D,BC⊥AD,垂足为点C.设∠ABC=α,下列关系式正确的是( )
A.sinα= B.sinα= C.sinα= D.sinα=
22.(3分)(2022 沈阳)如图,一条河的两岸互相平行,为了测量河的宽度PT(PT与河岸PQ垂直),测量得P,Q两点间距离为m米,∠PQT=α,则河宽PT的长为( )
A.msinα B.mcosα C.mtanα D.
23.(3分)(2021 十堰)如图,小明利用一个锐角是30°的三角板测操场旗杆的高度,已知他与旗杆之间的水平距离BC为15m,AB为1.5m(即小明的眼睛与地面的距离),那么旗杆的高度是( )
A.(15+)m B.5m C.15m D.(5+)m
24.(3分)(2022 黄石)我国魏晋时期的数学家刘徽首创“割圆术”:“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体,而无所失矣”,即通过圆内接正多边形割圆,从正六边形开始,每次边数成倍增加,依次可得圆内接正十二边形,内接正二十四边形,….边数越多割得越细,正多边形的周长就越接近圆的周长.再根据“圆周率等于圆周长与该圆直径的比”来计算圆周率.设圆的半径为R,图1中圆内接正六边形的周长l6=6R,则π≈=3.再利用圆的内接正十二边形来计算圆周率,则圆周率π约为( )
A.12sin15° B.12cos15° C.12sin30° D.12cos30°
25.(3分)(2022 福建)如图所示的衣架可以近似看成一个等腰三角形ABC,其中AB=AC,∠ABC=27°,BC=44cm,则高AD约为( )
(参考数据:sin27°≈0.45,cos27°≈0.89,tan27°≈0.51)
A.9.90cm B.11.22cm C.19.58cm D.22.44cm
26.(3分)(2021 长春)如图是净月潭国家森林公园一段索道的示意图.已知A、B两点间的距离为30米,∠A=α,则缆车从A点到达B点,上升的高度(BC的长)为( )
A.30sinα米 B.米 C.30cosα米 D.米
27.(3分)(2022 金华)一配电房示意图如图所示,它是一个轴对称图形.已知BC=6m,∠ABC=α,则房顶A离地面EF的高度为( )
A.(4+3sinα)m B.(4+3tanα)m C.(4+)m D.(4+)m
28.(3分)(2021 呼和浩特)如图,正方形的边长为4,剪去四个角后成为一个正八边形,则可求出此正八边形的外接圆直径d,根据我国魏晋时期数学家刘徽的“割圆术”思想,如果用此正八边形的周长近似代替其外接圆周长,便可估计π的值,下面d及π的值都正确的是( )
A.d=,π≈8sin22.5°
B.d=,π≈4sin22.5°
C.d=,π≈8sin22.5°
D.d=,π≈4sin22.5°
29.(3分)(2022 毕节市)如图,某地修建的一座建筑物的截面图的高BC=5m,坡面AB的坡度为1:,则AB的长度为( )
A.10m B.10m C.5m D.5m
30.(3分)(2022 黑龙江)小明去爬山,在山脚看山顶角度为30°,小明在坡比为5:12的山坡上走1300米,此时小明看山顶的角度为60°,山高为( )米
A.600﹣250 B.600﹣250 C.350+350 D.500
31.(3分)(2022 十堰)如图,坡角为α的斜坡上有一棵垂直于水平地面的大树AB,当太阳光线与水平线成45°角沿斜坡照下时,在斜坡上的树影BC长为m,则大树AB的高为( )
A.m(cosα﹣sinα) B.m(sinα﹣cosα)
C.m(cosα﹣tanα) D.﹣
32.(3分)(2021 德州)某商场准备改善原有楼梯的安全性能,把坡角由37°减至30°,已知原楼梯长为5米,调整后的楼梯会加长( )(参考数据:sin37°≈,cos37°≈,tan37°≈).
A.6米 B.3米 C.2米 D.1米
33.(3分)(2021 潍坊)如图,一束水平光线照在有一定倾斜角度的平面镜上,若入射光线与出射光线的夹角为60°,则平面镜的垂线与水平地面的夹角α的度数是( )
A.15° B.30° C.45° D.60°
34.(3分)(2022 随州)如图,已知点B,D,C在同一直线的水平地面上,在点C处测得建筑物AB的顶端A的仰角为α,在点D处测得建筑物AB的顶端A的仰角为β,若CD=α,则建筑物AB的高度为( )
A. B.
C. D.
35.(3分)(2021 济南)无人机低空遥感技术已广泛应用于农作物监测.如图,某农业特色品牌示范基地用无人机对一块试验田进行监测作业时,在距地面高度为135m的A处测得试验田右侧边界N处俯角为43°,无人机垂直下降40m至B处,又测得试验田左侧边界M处俯角为35°,则M,N之间的距离为( )(参考数据:tan43°≈0.9,sin43°≈0.7,cos35°≈0.8,tan35°≈0.7,结果保留整数)
A.188m B.269m C.286m D.312m
36.(3分)(2022 济南)数学活动小组到某广场测量标志性建筑AB的高度.如图,他们在地面上C点测得最高点A的仰角为22°,再向前70m至D点,又测得最高点A的仰角为58°,点C,D,B在同一直线上,则该建筑物AB的高度约为( )
(精确到1m.参考数据:sin22°≈0.37,tan22°≈0.40,sin58°≈0.85,tan58°≈1.60)
A.28m B.34m C.37m D.46m
37.(3分)(2022 贵港)如图,某数学兴趣小组测量一棵树CD的高度,在点A处测得树顶C的仰角为45°,在点B处测得树顶C的仰角为60°,且A,B,D三点在同一直线上,若AB=16m,则这棵树CD的高度是( )
A.8(3﹣)m B.8(3+)m C.6(3﹣)m D.6(3+)m
38.(3分)(2022 玉林)如图,从热气球A看一栋楼底部C的俯角是( )
A.∠BAD B.∠ACB C.∠BAC D.∠DAC
39.(3分)(2021 日照)如图,在一次数学实践活动中,小明同学要测量一座与地面垂直的古塔AB的高度,他从古塔底部点B处前行30m到达斜坡CE的底部点C处,然后沿斜坡CE前行20m到达最佳测量点D处,在点D处测得塔顶A的仰角为30°,已知斜坡的斜面坡度i=1:,且点A,B,C,D,E在同一平面内,小明同学测得古塔AB的高度是( )
A.(10+20)m B.(10+10)m C.20m D.40m
40.(3分)(2021 深圳)如图,在点F处,看建筑物顶端D的仰角为32°,向前走了15米到达点E即EF=15米,在点E处看点D的仰角为64°,则CD的长用三角函数表示为( )
A.15sin32° B.15tan64° C.15sin64° D.15tan32°
【真题汇编】2023年中考数学备考之锐角三角函数(选择题40题)
参考答案与试题解析
一.选择题(共40小题,满分120分,每小题3分)
1.(3分)(2022 荆州)如图,在平面直角坐标系中,点A,B分别在x轴负半轴和y轴正半轴上,点C在OB上,OC:BC=1:2,连接AC,过点O作OP∥AB交AC的延长线于P.若P(1,1),则tan∠OAP的值是( )
A. B. C. D.3
【解析】解:如图,过点P作PQ⊥x轴于点Q,
∵OP∥AB,
∴△OCP∽△BCA,
∴CP:AC=OC:BC=1:2,
∵∠AOC=∠AQP=90°,
∴CO∥PQ,
∴OQ:AO=CP:AC=1:2,
∵P(1,1),
∴PQ=OQ=1,
∴AO=2,
∴tan∠OAP===.
故选:C.
2.(3分)(2022 天津)tan45°的值等于( )
A.2 B.1 C. D.
【解析】解:tan45°的值等于1,
故选:B.
3.(3分)(2021 烟台)如图所示,若用我们数学课本上采用的科学计算器进行计算,其按键顺序及结果如下:
按键的结果为m;
按键的结果为n;
按键的结果为k.
下列判断正确的是( )
A.m=n B.n=k C.m=k D.m=n=k
【解析】解:m=23﹣=8﹣4=4;
n=﹣22=4﹣4=0;
k=﹣cos60°=﹣=4;
∴m=k,
故选:C.
4.(3分)(2021 威海)若用我们数学课本上采用的科学计算器计算sin36°18′,按键顺序正确的是( )
A.
B.
C.
D.
【解析】解:采用的科学计算器计算sin36°18′,按键顺序正确的是D选项中的顺序,
故选:D.
5.(3分)(2021 东营)如图,在△ABC中,∠C=90°,∠B=42°,BC=8,若用科学计算器求AC的长,则下列按键顺序正确的是( )
A.
B.
C.
D.
【解析】解:在△ABC中,因为∠C=90°,
所以tanB=,
因为∠B=42°,BC=8,
所以AC=BC tanB=8×tan42°.
故选:D.
6.(3分)(2021 桂林)如图,在平面直角坐标系内有一点P(3,4),连接OP,则OP与x轴正方向所夹锐角α的正弦值是( )
A. B. C. D.
【解析】解:作PA⊥x轴于A,如右图.
∵P(3,4),
∴OA=3,AP=4,
∴OP==5,
∴sinα=.
故选:D.
7.(3分)(2022 广西)如图,某博物馆大厅电梯的截面图中,AB的长为12米,AB与AC的夹角为α,则高BC是( )
A.12sinα米 B.12cosα米 C.米 D.米
【解析】解:Rt△ABC中,sinα=,
∵AB=12米,
∴BC=12sinα(米).
故选:A.
8.(3分)(2022 陕西)如图,AD是△ABC的高.若BD=2CD=6,tanC=2,则边AB的长为( )
A.3 B.3 C.3 D.6
【解析】解:∵2CD=6,
∴CD=3,
∵tanC=2,
∴=2,
∴AD=6,
在Rt△ABD中,由勾股定理得,
AB=,
故选:D.
9.(3分)(2022 通辽)如图,由边长为1的小正方形构成的网格中,点A,B,C都在格点上,以AB为直径的圆经过点C,D,则cos∠ADC的值为( )
A. B. C. D.
【解析】解:∵AB为直径,
∴∠ACB=90°,
又∵点A,B,C都在格点上,
∴∠ADC=∠ABC,
在Rt△ABC中,
cos∠ABC====cos∠ADC,
故选:B.
10.(3分)(2022 贵港)如图,在4×4网格正方形中,每个小正方形的边长为1,顶点为格点,若△ABC的顶点均是格点,则cos∠BAC的值是( )
A. B. C. D.
【解析】解:延长AC到D,连接BD,如图:
∵AD2=20,BD2=5,AB2=25,
∴AD2+BD2=AB2,
∴∠ADB=90°,
∴cos∠BAC===,
故选:C.
11.(3分)(2022 黔东南州)如图,PA、PB分别与⊙O相切于点A、B,连接PO并延长与⊙O交于点C、D,若CD=12,PA=8,则sin∠ADB的值为( )
A. B. C. D.
【解析】解连接AO,BO,
∵PA、PB分别与⊙O相切于点A、B,
∴∠PAO=∠PBO=90°,PA=PB=8,
∵DC=12,
∴AO=6,
∴OP=10,
在Rt△PAO和Rt△PBO中,
,
∴Rt△PAO≌Rt△PBO(HL),
∴∠AOP=∠BOP,
∴,
∴∠ADC=∠BDC,
∵∠AOC=2∠ADC,
∴∠ADB=∠AOC,
∴sin∠ADB=sin∠AOC==.
故选:A.
12.(3分)(2022 宜宾)如图,在矩形纸片ABCD中,AB=5,BC=3,将△BCD沿BD折叠到△BED位置,DE交AB于点F,则cos∠ADF的值为( )
A. B. C. D.
【解析】解:∵四边形ABCD是矩形,
∴∠A=90°,AB∥CD,AD=BC=3,AB=CD=5,
∴∠BDC=∠DBF,
由折叠的性质可得∠BDC=∠BDF,
∴∠BDF=∠DBF,
∴BF=DF,
设BF=x,则DF=x,AF=5﹣x,
在Rt△ADF中,32+(5﹣x)2=x2,
∴x=,
∴cos∠ADF=,
故选:C.
13.(3分)(2022 广元)如图,在正方形方格纸中,每个小正方形的边长都相等,A、B、C、D都在格点处,AB与CD相交于点P,则cos∠APC的值为( )
A. B. C. D.
【解析】解:把AB向上平移一个单位到DE,连接CE,如图.
则DE∥AB,
∴∠APC=∠EDC.
在△DCE中,有EC==,DC==2,DE==5,
∵EC2+DC2=DE2,
故△DCE为直角三角形,∠DCE=90°.
∴cos∠APC=cos∠EDC==.
故选:B.
14.(3分)(2021 巴中)如图,点A、B、C在边长为1的正方形网格格点上,下列结论错误的是( )
A.sinB= B.sinC=
C.tanB= D.sin2B+sin2C=1
【解析】解:由勾股定理得:AB=,AC=,BC=,
∴BC2=AB2+AC2,
∴△ABC是直角三角形,∠BAC=90°,
∴sinB=,sinC=,tanB=,sin2B+sin2C=,
故选:A.
15.(3分)(2022 陕西)如图,AD是△ABC的高.若BD=2CD=6,tanC=2,则边AB的长为( )
A.3 B.3 C.6 D.3
【解析】解:∵BD=2CD=6,
∴CD=3,BD=6,
∵tanC==2,
∴AD=6,
∴AB=AD=6
故选:C.
16.(3分)(2021 宜宾)如图,在△ABC中,点O是角平分线AD、BE的交点,若AB=AC=10,BC=12,则tan∠OBD的值是( )
A. B.2 C. D.
【解析】解:如图:
作OF⊥AB于F,
∵AB=AC,AD平分∠BAC.
∴∠ODB=90°.BD=CD=6.
∴根据勾股定理得:AD==8.
∵BE平分∠ABC.
∴OF=OD,BF=BD=6,AF=10﹣6=4.
设OD=OF=x,则AO=8﹣x,在Rt△AOF中,根据勾股定理得:
(8﹣x)2=x2+42.
∴x=3.
∴OD=3.
在Rt△OBD中,tan∠OBD===.
法二:在求出AF=4后
∵tan∠BAD==.
∴=.
∴OF=3.
∴OD=OF=3.
∴tan∠OBD==.
故选:A.
17.(3分)(2022 乐山)如图,在Rt△ABC中,∠C=90°,BC=,点D是AC上一点,连结BD.若tan∠A=,tan∠ABD=,则CD的长为( )
A.2 B.3 C. D.2
【解析】解:过D点作DE⊥AB于E,
∵tan∠A==,tan∠ABD==,
∴AE=2DE,BE=3DE,
∴2DE+3DE=5DE=AB,
在Rt△ABC中,tan∠A=,BC=,
∴,
解得AC=,
∴AB=,
∴DE=1,
∴AE=2,
∴AD=,
∴CD=AC﹣AD=,
故选:C.
18.(3分)(2022 泸州)如图,在平面直角坐标系xOy中,矩形OABC的顶点B的坐标为(10,4),四边形ABEF是菱形,且tan∠ABE=.若直线l把矩形OABC和菱形ABEF组成的图形的面积分成相等的两部分,则直线l的解析式为( )
A.y=3x B.y=﹣x+ C.y=﹣2x+11 D.y=﹣2x+12
【解析】解:连接OB,AC,它们交于点M,连接AE,BF,它们交于点N,
则直线MN为符合条件的直线l,如图,
∵四边形OABC是矩形,
∴OM=BM.
∵B的坐标为(10,4),
∴M(5,2),AB=10,BC=4.
∵四边形ABEF为菱形,
BE=AB=10.
过点E作EG⊥AB于点G,
在Rt△BEG中,
∵tan∠ABE=,
∴,
设EG=4k,则BG=3k,
∴BE==5k,
∴5k=10,
∴k=2,
∴EG=8,BG=6,
∴AG=4.
∴E(4,12).
∵B的坐标为(10,4),AB∥x轴,
∴A(0,4).
∵点N为AE的中点,
∴N(2,8).
设直线l的解析式为y=ax+b,
∴,
解得:,
∴直线l的解析式为y=﹣2x+12,
故选:D.
19.(3分)(2021 黑龙江)如图,在△ABC中,∠ACB=90°,点D在AB的延长线上,连接CD,若AB=2BD,tan∠BCD=,则的值为( )
A.1 B.2 C. D.
【解析】解:过点D作DM⊥BC,交CB的延长线于点M,
∵∠ACB=∠DMB=90°,∠ABC=∠DBM,
∴△ABC∽△DBM,
∴==,
∵AB=2BD,
∴===,
在Rt△CDM中,
由于tan∠MCD==,设DM=2k,则CM=3k,
又∵==,
∴BC=2k,AC=4k,
∴==2,
故选:B.
20.(3分)(2021 淄博)如图,在Rt△ABC中,∠ACB=90°,CE是斜边AB上的中线,过点E作EF⊥AB交AC于点F.若BC=4,△AEF的面积为5,则sin∠CEF的值为( )
A. B. C. D.
【解析】解:连接BF,
∵CE是斜边AB上的中线,EF⊥AB,
∴EF是AB的垂直平分线,
∴S△AFE=S△BFE=5,∠FBA=∠A,
∴S△AFB=10=AF BC,
∵BC=4,
∴AF=5=BF,
在Rt△BCF中,BC=4,BF=5,
∴CF==3,
∵CE=AE=BE=AB,
∴∠A=∠FBA=∠ACE,
又∵∠BCA=90°=∠BEF,
∴∠CBF=90°﹣∠BFC=90°﹣2∠A,
∠CEF=90°﹣∠BEC=90°﹣2∠A,
∴∠CEF=∠FBC,
∴sin∠CEF=sin∠FBC==,
故选:A.
21.(3分)(2022 长春)如图是长春市人民大街下穿隧道工程施工现场的一台起重机的示意图,该起重机的变幅索顶端记为点A,变幅索的底端记为点B,AD垂直地面,垂足为点D,BC⊥AD,垂足为点C.设∠ABC=α,下列关系式正确的是( )
A.sinα= B.sinα= C.sinα= D.sinα=
【解析】解:在Rt△ABC中,∠ACB=90°,∠ABC=α,由锐角三角函数的定义可知,
sinα=sin∠ABC=,
故选:D.
22.(3分)(2022 沈阳)如图,一条河的两岸互相平行,为了测量河的宽度PT(PT与河岸PQ垂直),测量得P,Q两点间距离为m米,∠PQT=α,则河宽PT的长为( )
A.msinα B.mcosα C.mtanα D.
【解析】解:由题意得:
PT⊥PQ,
∴∠APQ=90°,
在Rt△APQ中,PQ=m米,∠PQT=α,
∴PT=PQ tanα=mtanα(米),
∴河宽PT的长度是mtanα米,
故选:C.
23.(3分)(2021 十堰)如图,小明利用一个锐角是30°的三角板测操场旗杆的高度,已知他与旗杆之间的水平距离BC为15m,AB为1.5m(即小明的眼睛与地面的距离),那么旗杆的高度是( )
A.(15+)m B.5m C.15m D.(5+)m
【解析】解:由题意可得,四边形ABCD是矩形,BC=15m,AB=1.5m,
∴BC=AD=15m,AB=CD=1.5m,
在Rt△ADE中,∠EAD=30°,AD=15m,
∴DE=AD tan∠EAD=15×=5(m),
∴CE=CD+DE=(5+1.5)(m).
故选:D.
24.(3分)(2022 黄石)我国魏晋时期的数学家刘徽首创“割圆术”:“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体,而无所失矣”,即通过圆内接正多边形割圆,从正六边形开始,每次边数成倍增加,依次可得圆内接正十二边形,内接正二十四边形,….边数越多割得越细,正多边形的周长就越接近圆的周长.再根据“圆周率等于圆周长与该圆直径的比”来计算圆周率.设圆的半径为R,图1中圆内接正六边形的周长l6=6R,则π≈=3.再利用圆的内接正十二边形来计算圆周率,则圆周率π约为( )
A.12sin15° B.12cos15° C.12sin30° D.12cos30°
【解析】解:在正十二边形中,∠A6OM=360°÷24=15°,
∴A6M=sin15°×OA6=R×sin15°,
∵OA6=OA7,OM⊥A6A7,
∴A6A7=2A6M=2R×sin15°,
∴π≈=12sin15°,
故选:A.
25.(3分)(2022 福建)如图所示的衣架可以近似看成一个等腰三角形ABC,其中AB=AC,∠ABC=27°,BC=44cm,则高AD约为( )
(参考数据:sin27°≈0.45,cos27°≈0.89,tan27°≈0.51)
A.9.90cm B.11.22cm C.19.58cm D.22.44cm
【解析】解:∵AB=AC,BC=44cm,
∴BD=CD=22cm,AD⊥BC,
∵∠ABC=27°,
∴tan∠ABC=≈0.51,
∴AD≈0.51×22=11.22cm,
故选:B.
26.(3分)(2021 长春)如图是净月潭国家森林公园一段索道的示意图.已知A、B两点间的距离为30米,∠A=α,则缆车从A点到达B点,上升的高度(BC的长)为( )
A.30sinα米 B.米 C.30cosα米 D.米
【解析】解:由图可知,在△ABC中,AC⊥BC,
∴sinα==,
∴BC=30sinα米.
故选:A.
27.(3分)(2022 金华)一配电房示意图如图所示,它是一个轴对称图形.已知BC=6m,∠ABC=α,则房顶A离地面EF的高度为( )
A.(4+3sinα)m B.(4+3tanα)m C.(4+)m D.(4+)m
【解析】解:过点A作AD⊥BC于点D,如图,
∵它是一个轴对称图形,
∴AB=AC,
∵AD⊥BC,
∴BD=BC=3m,
在Rt△ADB中,
∵tan∠ABC=,
∴AD=BD tanα=3tanαm.
∴房顶A离地面EF的高度=AD+BE=(4+3tanα)m,
故选:B.
28.(3分)(2021 呼和浩特)如图,正方形的边长为4,剪去四个角后成为一个正八边形,则可求出此正八边形的外接圆直径d,根据我国魏晋时期数学家刘徽的“割圆术”思想,如果用此正八边形的周长近似代替其外接圆周长,便可估计π的值,下面d及π的值都正确的是( )
A.d=,π≈8sin22.5°
B.d=,π≈4sin22.5°
C.d=,π≈8sin22.5°
D.d=,π≈4sin22.5°
【解析】解:如图,连接AD,BC交于点O,过点O作OP⊥BC于点P,
则CP=PD,且∠COP=22.5°,
设正八边形的边长为a,则a+2×a=4,
解得a=4(﹣1),
在Rt△OCP中,OC==,
∴d=2OC=,
由πd≈8CD,
则π≈32(﹣1),
∴π≈8sin22.5°.
故选:C.
29.(3分)(2022 毕节市)如图,某地修建的一座建筑物的截面图的高BC=5m,坡面AB的坡度为1:,则AB的长度为( )
A.10m B.10m C.5m D.5m
【解析】解:∵坡面AB的坡度为==1:,
∴AC=5m,
∴AB==10m.
故选:A.
30.(3分)(2022 黑龙江)小明去爬山,在山脚看山顶角度为30°,小明在坡比为5:12的山坡上走1300米,此时小明看山顶的角度为60°,山高为( )米
A.600﹣250 B.600﹣250 C.350+350 D.500
【解析】解:设EF=5x米,
∵斜坡BE的坡度为5:12,
∴BF=12x米,
由勾股定理得:(5x)2+(12x)2=(1300)2,
解得:x=100,
则EF=500米,BF=1200米,
由题意可知,四边形DCFE为矩形,
∴DC=EF=500米,DE=CF,
在Rt△ADE中,tan∠AED=,
则DE==AD,
在Rt△ACB中,tan∠ABC=,
∴=,
解得:AD=600﹣750,
∴山高AC=AD+DC=600﹣750+500=(600﹣250)米,
故选:B.
31.(3分)(2022 十堰)如图,坡角为α的斜坡上有一棵垂直于水平地面的大树AB,当太阳光线与水平线成45°角沿斜坡照下时,在斜坡上的树影BC长为m,则大树AB的高为( )
A.m(cosα﹣sinα) B.m(sinα﹣cosα)
C.m(cosα﹣tanα) D.﹣
【解析】解:过点C作水平地面的平行线,交AB的延长线于D,
则∠BCD=α,
在Rt△BCD中,BC=m,∠BCD=α,
则BD=BC sin∠BCD=msinα,CD=BC cos∠BCD=mcosα,
在Rt△ACD中,∠ACD=45°,
则AD=CD=mcosα,
∴AB=AD﹣BD=mcosα﹣msinα=m(cosα﹣sinα),
故选:A.
32.(3分)(2021 德州)某商场准备改善原有楼梯的安全性能,把坡角由37°减至30°,已知原楼梯长为5米,调整后的楼梯会加长( )(参考数据:sin37°≈,cos37°≈,tan37°≈).
A.6米 B.3米 C.2米 D.1米
【解析】解:在Rt△BAD中,AB=5米,∠BAD=37°,
则BD=AB sin∠BAD≈5×=3(米),
在Rt△BCD中,∠C=30°,
∴BC=2BD=6(米),
则调整后的楼梯会加长:6﹣5=1(米),
故选:D.
33.(3分)(2021 潍坊)如图,一束水平光线照在有一定倾斜角度的平面镜上,若入射光线与出射光线的夹角为60°,则平面镜的垂线与水平地面的夹角α的度数是( )
A.15° B.30° C.45° D.60°
【解析】解:如图,作CD⊥平面镜,垂足为G,交地面于D.
∵EF⊥平面镜,
∴CD∥EF,
∴∠CDH=∠EFH=α,
根据题意可知:AG∥DF,
∴∠AGC=∠CDH=α,
∴∠AGC=α,
∵∠AGC=AGB=×60°=30°,
∴α=30°.
故选:B.
34.(3分)(2022 随州)如图,已知点B,D,C在同一直线的水平地面上,在点C处测得建筑物AB的顶端A的仰角为α,在点D处测得建筑物AB的顶端A的仰角为β,若CD=α,则建筑物AB的高度为( )
A. B.
C. D.
【解析】解:设AB=x,
在Rt△ABD中,tanβ=,
∴BD=,
∴BC=BD+CD=a+,
在Rt△ABC中,tanα=,
解得x=.
故选:D.
35.(3分)(2021 济南)无人机低空遥感技术已广泛应用于农作物监测.如图,某农业特色品牌示范基地用无人机对一块试验田进行监测作业时,在距地面高度为135m的A处测得试验田右侧边界N处俯角为43°,无人机垂直下降40m至B处,又测得试验田左侧边界M处俯角为35°,则M,N之间的距离为( )(参考数据:tan43°≈0.9,sin43°≈0.7,cos35°≈0.8,tan35°≈0.7,结果保留整数)
A.188m B.269m C.286m D.312m
【解析】解:由题意得:∠N=43°,∠M=35°,AO=135m,BO=AO﹣AB=95m,
在Rt△AON中,
tanN==tan43°,
∴NO=≈150m,
在Rt△BOM中,
tanM==tan35°,
∴MO=≈135.7m,
∴MN=MO+NO=135.7+150≈286m.
故选:C.
36.(3分)(2022 济南)数学活动小组到某广场测量标志性建筑AB的高度.如图,他们在地面上C点测得最高点A的仰角为22°,再向前70m至D点,又测得最高点A的仰角为58°,点C,D,B在同一直线上,则该建筑物AB的高度约为( )
(精确到1m.参考数据:sin22°≈0.37,tan22°≈0.40,sin58°≈0.85,tan58°≈1.60)
A.28m B.34m C.37m D.46m
【解析】解:由题意可知:AB⊥BC,
在Rt△ADB中,∠B=90°,∠ADB=58°,
∵tan∠ADB=tan58°=,
∴BD=≈(m),
在Rt△ACB中,∠B=90°,∠C=22°,
∵CD=70m,
∴BC=CD+BD=(70+)m,
∴AB=BC×tanC≈(70+)×0.40(m),
解得:AB≈37m,
答:该建筑物AB的高度约为37m.
故选:C.
37.(3分)(2022 贵港)如图,某数学兴趣小组测量一棵树CD的高度,在点A处测得树顶C的仰角为45°,在点B处测得树顶C的仰角为60°,且A,B,D三点在同一直线上,若AB=16m,则这棵树CD的高度是( )
A.8(3﹣)m B.8(3+)m C.6(3﹣)m D.6(3+)m
【解析】解:设AD=x米,
∵AB=16米,
∴BD=AB﹣AD=(16﹣x)米,
在Rt△ADC中,∠A=45°,
∴CD=AD tan45°=x(米),
在Rt△CDB中,∠B=60°,
∴tan60°===,
∴x=24﹣8,
经检验:x=24﹣8是原方程的根,
∴CD=24﹣8=8(3﹣))米,
∴这棵树CD的高度是8(3﹣)米,
故选:A.
38.(3分)(2022 玉林)如图,从热气球A看一栋楼底部C的俯角是( )
A.∠BAD B.∠ACB C.∠BAC D.∠DAC
【解析】解:从热气球A看一栋楼底部C的俯角是∠DAC.
故选:D.
39.(3分)(2021 日照)如图,在一次数学实践活动中,小明同学要测量一座与地面垂直的古塔AB的高度,他从古塔底部点B处前行30m到达斜坡CE的底部点C处,然后沿斜坡CE前行20m到达最佳测量点D处,在点D处测得塔顶A的仰角为30°,已知斜坡的斜面坡度i=1:,且点A,B,C,D,E在同一平面内,小明同学测得古塔AB的高度是( )
A.(10+20)m B.(10+10)m C.20m D.40m
【解析】解:过D作DF⊥BC于F,DH⊥AB于H,
∴DH=BF,BH=DF,
∵斜坡的斜面坡度i=1:,
∴=1:,
设DF=xm,CF=xm,
∴CD==2xm=20m,
∴x=10,
∴BH=DF=10m,CF=10m,
∴DH=BF=(10+30)m,
∵∠ADH=30°,
∴AH=DH=×(10+30)=(10+10)m,
∴AB=AH+BH=(20+10)m,
故选:A.
40.(3分)(2021 深圳)如图,在点F处,看建筑物顶端D的仰角为32°,向前走了15米到达点E即EF=15米,在点E处看点D的仰角为64°,则CD的长用三角函数表示为( )
A.15sin32° B.15tan64° C.15sin64° D.15tan32°
【解析】解:∵∠CED=64°,∠F=32°,∠CED=∠F+∠EDF,
∴∠EDF=∠CED﹣∠F=64°﹣32°=32°,
∴∠EDF=∠F,
∴DE=EF,
∵EF=15米,
∴DE=15米,
在Rt△CDE中,
∵sin∠CED=,
∴CD=DEsin∠CED=15sin64°,
故选:C.
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
