专题32 反比例函数(选择题60题)(含解析)-【冲刺2023中考】真题冲刺专题(知识点+专题训练)
文档属性
| 名称 | 专题32 反比例函数(选择题60题)(含解析)-【冲刺2023中考】真题冲刺专题(知识点+专题训练) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-12 09:53:12 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
【真题汇编】2023年中考数学备考之反比例函数
1.反比例函数的图象
用描点法画反比例函数的图象,步骤:列表﹣﹣﹣描点﹣﹣﹣连线.
(1)列表取值时,x≠0,因为x=0函数无意义,为了使描出的点具有代表性,可以以“0”为中心,向两边对称式取值,即正、负数各一半,且互为相反数,这样也便于求y值.
(2)由于函数图象的特征还不清楚,所以要尽量多取一些数值,多描一些点,这样便于连线,使画出的图象更精确.
(3)连线时要用平滑的曲线按照自变量从小到大的顺序连接,切忌画成折线.
(4)由于x≠0,k≠0,所以y≠0,函数图象永远不会与x轴、y轴相交,只是无限靠近两坐标轴.
2.反比例函数的性质
反比例函数的性质
(1)反比例函数y=(k≠0)的图象是双曲线;
(2)当k>0,双曲线的两支分别位于第一、第三象限,在每一象限内y随x的增大而减小;
(3)当k<0,双曲线的两支分别位于第二、第四象限,在每一象限内y随x的增大而增大.
注意:反比例函数的图象与坐标轴没有交点.
3.反比例函数系数k的几何意义
比例系数k的几何意义
在反比例函数y=图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.
在反比例函数的图象上任意一点向坐标轴作垂线,这一点和垂足以及坐标原点所构成的三角形的面积是|k|,且保持不变.
4.反比例函数图象上点的坐标特征
反比例函数y=k/x(k为常数,k≠0)的图象是双曲线,
①图象上的点(x,y)的横纵坐标的积是定值k,即xy=k;
②双曲线是关于原点对称的,两个分支上的点也是关于原点对称;
③在y=k/x图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.
5.待定系数法求反比例函数解析式
用待定系数法求反比例函数的解析式要注意:
(1)设出含有待定系数的反比例函数解析式y=(k为常数,k≠0);
(2)把已知条件(自变量与函数的对应值)带入解析式,得到待定系数的方程;
(3)解方程,求出待定系数;
(4)写出解析式.
6.反比例函数与一次函数的交点问题
反比例函数与一次函数的交点问题
(1)求反比例函数与一次函数的交点坐标,把两个函数关系式联立成方程组求解,若方程组有解则两者有交点,方程组无解,则两者无交点.
(2)判断正比例函数y=k1x和反比例函数y=在同一直角坐标系中的交点个数可总结为:
①当k1与k2同号时,正比例函数y=k1x和反比例函数y=在同一直角坐标系中有2个交点;
②当k1与k2异号时,正比例函数y=k1x和反比例函数y=在同一直角坐标系中有0个交点.
7.反比例函数的应用
(1)利用反比例函数解决实际问题
①能把实际的问题转化为数学问题,建立反比例函数的数学模型.②注意在自变量和函数值的取值上的实际意义.③问题中出现的不等关系转化成相等的关系来解,然后在作答中说明.
(2)跨学科的反比例函数应用题
要熟练掌握物理或化学学科中的一些具有反比例函数关系的公式.同时体会数学中的转化思想.
(3)反比例函数中的图表信息题
正确的认识图象,找到关键的点,运用好数形结合的思想.
8.反比例函数综合题
(1)应用类综合题
能够从实际的问题中抽象出反比例函数这一数学模型,是解决实际问题的关键一步,培养了学生的建模能力和从实际问题向数学问题转化的能力.在解决这些问题的时候我们还用到了反比例函数的图象和性质、待定系数法和其他学科中的知识.
(2)数形结合类综合题
利用图象解决问题,从图上获取有用的信息,是解题的关键所在.已知点在图象上,那么点一定满足这个函数解析式,反过来如果这点满足函数的解析式,那么这个点也一定在函数图象上.还能利用图象直接比较函数值或是自变量的大小.将数形结合在一起,是分析解决问题的一种好方法.
【真题汇编】2023年中考数学备考之反比例函数
(选择题60题)
满分:120分 建议时间:100分钟
学校:___________姓名:___________班级:___________考号:___________
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息2.请将答案正确填写在答题卡上
一.选择题(共60小题,满分120分,每小题2分)
1.(2分)(2022 襄阳)二次函数y=ax2+bx+c的图象如图所示,则一次函数y=bx+c和反比例函数y=在同一平面直角坐标系中的图象可能是( )
A. B.
C. D.
2.(2分)(2022 西藏)在同一平面直角坐标系中,函数y=ax+b与y=(其中a,b是常数,ab≠0)的大致图象是( )
A. B.
C. D.
3.(2分)(2022 张家界)在同一平面直角坐标系中,函数y=kx+1(k≠0)和y=(k≠0)的图象大致是( )
A. B.
C. D.
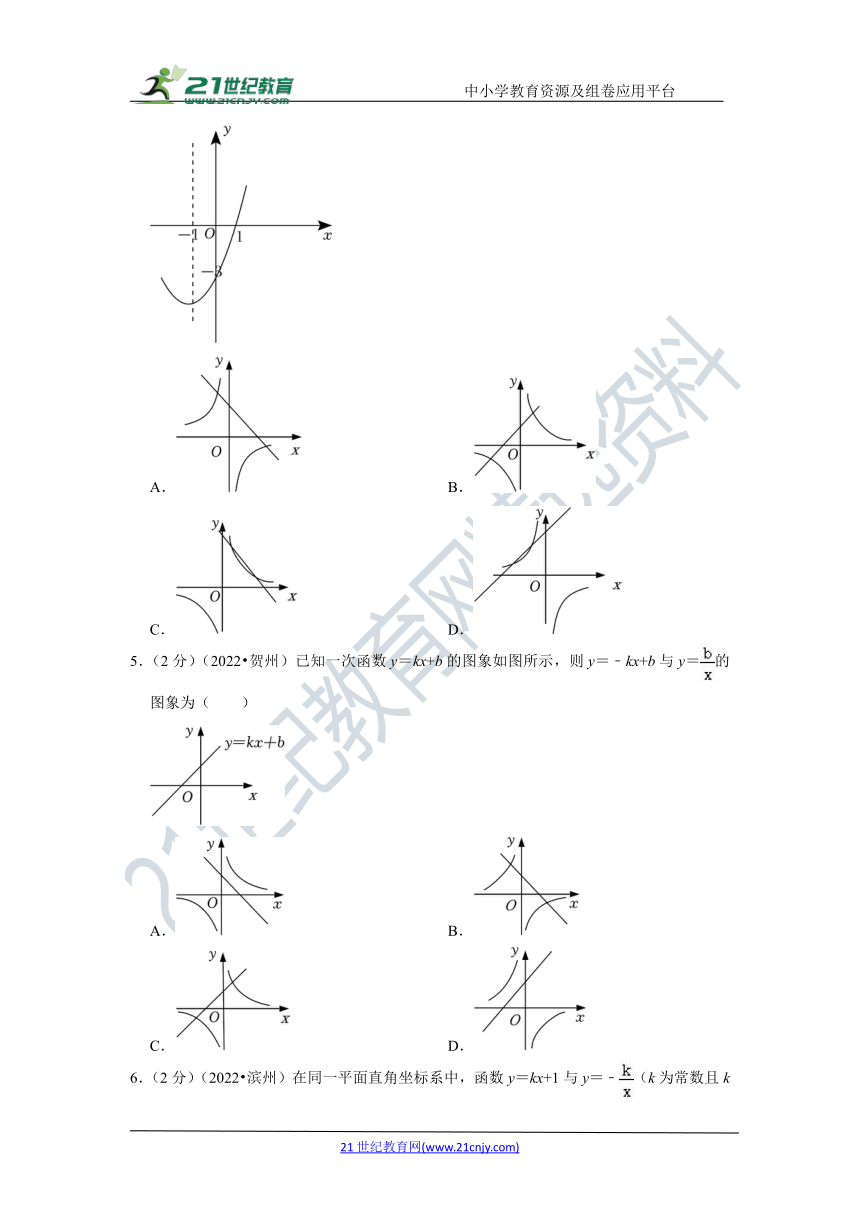
4.(2分)(2022 绥化)已知二次函数y=ax2+bx+c的部分函数图象如图所示,则一次函数y=ax+b2﹣4ac与反比例函数y=在同一平面直角坐标系中的图象大致是( )
A. B.
C. D.
5.(2分)(2022 贺州)已知一次函数y=kx+b的图象如图所示,则y=﹣kx+b与y=的图象为( )
A. B.
C. D.
6.(2分)(2022 滨州)在同一平面直角坐标系中,函数y=kx+1与y=﹣(k为常数且k≠0)的图象大致是( )
A. B.
C. D.
7.(2分)(2021 遵义)已知反比例函数y=(k≠0)的图象如图所示,则一次函数y=kx+2的图象经过( )
A.第一、二、三象限 B.第一、三、四象限
C.第一、二、四象限 D.第二、三、四象限
8.(2分)(2022 黔西南州)在平面直角坐标系中,反比例函数y=(k≠0)的图象如图所示,则一次函数y=kx+2的图象经过的象限是( )
A.一、二、三 B.一、二、四 C.一、三、四 D.二、三、四
9.(2分)(2022 上海)已知反比例函数y=(k≠0),且在各自象限内,y随x的增大而增大,则下列点可能在这个函数图象上的为( )
A.(2,3) B.(﹣2,3) C.(3,0) D.(﹣3,0)
10.(2分)(2022 广东)点(1,y1),(2,y2),(3,y3),(4,y4)在反比例函数y=图象上,则y1,y2,y3,y4中最小的是( )
A.y1 B.y2 C.y3 D.y4
11.(2分)(2021 黔西南州)对于反比例函数y=,下列说法错误的是( )
A.图象经过点(1,﹣5)
B.图象位于第二、第四象限
C.当x<0时,y随x的增大而减小
D.当x>0时,y随x的增大而增大
12.(2分)(2022 荆门)如图,点A,C为函数y=(x<0)图象上的两点,过A,C分别作AB⊥x轴,CD⊥x轴,垂足分别为B,D,连接OA,AC,OC,线段OC交AB于点E,且点E恰好为OC的中点.当△AEC的面积为时,k的值为( )
A.﹣1 B.﹣2 C.﹣3 D.﹣4
13.(2分)(2021 德州)小红同学在研究函数y=|x|+的图象时,发现有如下结论:①该函数有最小值;②该函数图象与坐标轴无交点;③当x>0时,y随x的增大而增大;④该函数图象关于y轴对称;⑤直线y=8与该函数图象有两个交点,则上述结论中正确的个数为( )
A.2个 B.3个 C.4个 D.5个
14.(2分)(2021 济南)反比例函数y=(k≠0)图象的两个分支分别位于第一、三象限,则一次函数y=kx﹣k的图象大致是( )
A. B. C. D.
15.(2分)(2021 阜新)已知点A(x1,y1),B(x2,y2)都在反比例函数y=﹣的图象上,且x1<0<x2,则y1,y2的关系一定成立的是( )
A.y1>y2 B.y1<y2 C.y1+y2=0 D.y1﹣y2=0
16.(2分)(2021 湘西州)如图所示,小英同学根据学习函数的经验,自主尝试在平面直角坐标系中画出了一个解析式为y=的函数图象.根据这个函数的图象,下列说法正确的是( )
A.图象与x轴没有交点
B.当x>0时,y>0
C.图象与y轴的交点是(0,﹣)
D.y随x的增大而减小
17.(2分)(2021 兰州)如图,点A在反比例函数y=(x>0)图象上,AB⊥x轴于点B,C是OB的中点,连接AO,AC,若△AOC的面积为2,则k=( )
A.4 B.8 C.12 D.16
18.(2分)(2022 日照)如图,矩形OABC与反比例函数y1=(k1是非零常数,x>0)的图象交于点M,N,与反比例函数y2=(k2是非零常数,x>0)的图象交于点B,连接OM,ON.若四边形OMBN的面积为3,则k1﹣k2=( )
A.3 B.﹣3 C. D.
19.(2分)(2022 牡丹江)如图,等边三角形OAB,点B在x轴正半轴上,S△OAB=4,若反比例函数y=(k≠0)图象的一支经过点A,则k的值是( )
A. B. C. D.
20.(2分)(2022 通辽)如图,点D是 OABC内一点,AD与x轴平行,BD与y轴平行,BD=,∠BDC=120°,S△BCD=,若反比例函数y=(x<0)的图象经过C,D两点,则k的值是( )
A.﹣6 B.﹣6 C.﹣12 D.﹣12
21.(2分)(2022 郴州)如图,在函数y=(x>0)的图象上任取一点A,过点A作y轴的垂线交函数y=﹣(x<0)的图象于点B,连接OA,OB,则△AOB的面积是( )
A.3 B.5 C.6 D.10
22.(2分)(2021 牡丹江)如图,矩形OABC的面积为36,它的对角线OB与双曲线y=相交于点D,且OD:OB=2:3,则k的值为( )
A.12 B.﹣12 C.16 D.﹣16
23.(2分)(2022 黑龙江)如图,在平面直角坐标系中,点O为坐标原点,平行四边形OBAD的顶点B在反比例函数y=的图象上,顶点A在反比例函数y=的图象上,顶点D在x轴的负半轴上.若平行四边形OBAD的面积是5,则k的值是( )
A.2 B.1 C.﹣1 D.﹣2
24.(2分)(2022 十堰)如图,正方形ABCD的顶点分别在反比例函数y=(k1>0)和y=(k2>0)的图象上.若BD∥y轴,点D的横坐标为3,则k1+k2=( )
A.36 B.18 C.12 D.9
25.(2分)(2021 兰州)如图,点A在反比例函数y=(x>0)的图象上,AB⊥x轴于点B,C是OB的中点,连接AO,AC,若△AOC的面积为4,则k=( )
A.16 B.12 C.8 D.4
26.(2分)(2021 西藏)如图.在平面直角坐标系中,△AOB的面积为,BA垂直x轴于点A,OB与双曲线y=相交于点C,且BC:OC=1:2.则k的值为( )
A.﹣3 B.﹣ C.3 D.
27.(2分)(2021 丹东)如图,点A在双曲线y1=(x>0)上,点B在双曲线y2=(x<0)上,AB∥x轴,点C是x轴上一点,连接AC、BC,若△ABC的面积是6,则k的值( )
A.﹣6 B.﹣8 C.﹣10 D.﹣12
28.(2分)(2021 黑龙江)如图,在平面直角坐标系中,矩形ABCD的顶点A在双曲线y=﹣(x<0)上,点C,D在y轴的正半轴上,点E在BC上,CE=2BE,连接DE并延长,交x轴于点F,连接CF,则△FCD的面积为( )
A.2 B. C.1 D.
29.(2分)(2021 淄博)如图,在平面直角坐标系中,四边形AOBD的边OB与x轴的正半轴重合,AD∥OB,DB⊥x轴,对角线AB,OD交于点M.已知AD:OB=2:3,△AMD的面积为4.若反比例函数y=的图象恰好经过点M,则k的值为( )
A. B. C. D.12
30.(2分)(2021 兴安盟)点(﹣5,y1),(﹣3,y2),(3,y3)都在反比例函数y=(k>0)的图象上,则( )
A.y1>y2>y3 B.y3>y1>y2 C.y2>y1>y3 D.y1>y3>y2
31.(2分)(2021 德州)已知点A(x1,y1),B(x2,y2),C(x3,y3)都在反比例函数y=(a是常数)的图象上,且y1<y2<0<y3,则x1,x2,x3的大小关系为( )
A.x2>x1>x3 B.x1>x2>x3 C.x3>x2>x1 D.x3>x1>x2
32.(2分)(2022 阜新)已知反比例函数y=(k≠0)的图象经过点(﹣2,4),那么该反比例函数图象也一定经过点( )
A.(4,2) B.(1,8) C.(﹣1,8) D.(﹣1,﹣8)
33.(2分)(2022 襄阳)若点A(﹣2,y1),B(﹣1,y2)都在反比例函数y=的图象上,则y1,y2的大小关系是( )
A.y1<y2 B.y1=y2 C.y1>y2 D.不能确定
34.(2分)(2022 枣庄)如图,正方形ABCD的边长为5,点A的坐标为(4,0),点B在y轴上,若反比例函数y=(k≠0)的图象过点C,则k的值为( )
A.4 B.﹣4 C.﹣3 D.3
35.(2分)(2022 长春)如图,在平面直角坐标系中,点P在反比例函数y=(k>0,x>0)的图象上,其纵坐标为2,过点P作PQ∥y轴,交x轴于点Q,将线段QP绕点Q顺时针旋转60°得到线段QM.若点M也在该反比例函数的图象上,则k的值为( )
A. B. C. D.4
36.(2分)(2022 贵阳)如图,在平面直角坐标系中有P,Q,M,N四个点,其中恰有三点在反比例函数y=(k>0)的图象上.根据图中四点的位置,判断这四个点中不在函数y=的图象上的点是( )
A.点P B.点Q C.点M D.点N
37.(2分)(2022 娄底)在平面直角坐标系中,O为坐标原点,已知点P(m,1)、Q(1,m)(m>0且m≠1),过点P、Q的直线与两坐标轴相交于A、B两点,连接OP、OQ,则下列结论中成立的有( )
①点P、Q在反比例函数y=的图象上;
②△AOB为等腰直角三角形;
③0°<∠POQ<90°;
④∠POQ的值随m的增大而增大.
A.②③④ B.①③④ C.①②④ D.①②③
38.(2分)(2022 天津)若点A(x1,2),B(x2,﹣1),C(x3,4)都在反比例函数y=的图象上,则x1,x2,x3的大小关系是( )
A.x1<x2<x3 B.x2<x3<x1 C.x1<x3<x2 D.x2<x1<x3
39.(2分)(2021 内江)如图,菱形ABCD的顶点分别在反比例函数y=和y=的图象上,若∠BCD=60°,则的值为( )
A. B. C. D.
40.(2分)(2021 朝阳)如图,O是坐标原点,点B在x轴上,在△OAB中,AO=AB=5,OB=6,点A在反比例函数y=(k≠0)图象上,则k的值( )
A.﹣12 B.﹣15 C.﹣20 D.﹣30
41.(2分)(2021 大连)下列说法正确的是( )
①反比例函数y=中自变量x的取值范围是x≠0;
②点P(﹣3,2)在反比例函数y=﹣的图象上;
③反比例函数y=的图象,在每一个象限内,y随x的增大而增大.
A.①② B.①③ C.②③ D.①②③
42.(2分)(2022 海南)若反比例函数y=(k≠0)的图象经过点(2,﹣3),则它的图象也一定经过的点是( )
A.(﹣2,﹣3) B.(﹣3,﹣2) C.(1,﹣6) D.(6,1)
43.(2分)(2022 武汉)已知点A(x1,y1),B(x2,y2)在反比例函数y=的图象上,且x1<0<x2,则下列结论一定正确的是( )
A.y1+y2<0 B.y1+y2>0 C.y1<y2 D.y1>y2
44.(2分)(2022 宿迁)如图,点A在反比例函数y=(x>0)的图象上,以OA为一边作等腰直角三角形OAB,其中∠OAB=90°,AO=AB,则线段OB长的最小值是( )
A.1 B. C.2 D.4
45.(2分)(2021 益阳)正比例函数y=2x与反比例函数y=的图象或性质的共有特征之一是( )
A.函数值y随x的增大而增大
B.图象在第一、三象限都有分布
C.图象与坐标轴有交点
D.图象经过点(2,1)
46.(2分)(2021 滨州)如图,在△OAB中,∠BOA=45°,点C为边AB上一点,且BC=2AC.如果函数y=(x>0)的图象经过点B和点C,那么用下列坐标表示的点,在直线BC上的是( )
A.(﹣2019,674) B.(﹣2020,675)
C.(2021,﹣669) D.(2022,﹣670)
47.(2分)(2021 广州)在平面直角坐标系xOy中,矩形OABC的顶点A在函数y=(x>0)的图象上,顶点C在函数y=﹣(x<0)的图象上,若顶点B的横坐标为﹣,则点A的坐标为( )
A.(,2) B.(,) C.(2,) D.(,)
48.(2分)(2022 东营)如图,一次函数y1=k1x+b与反比例函数y2=的图象相交于A,B两点,点A的横坐标为2,点B的横坐标为﹣1,则不等式k1x+b<的解集是( )
A.﹣1<x<0或x>2 B.x<﹣1或0<x<2
C.x<﹣1或x>2 D.﹣1<x<2
49.(2分)(2022 无锡)一次函数y=mx+n的图象与反比例函数y=的图象交于点A、B,其中点A、B的坐标为A(﹣,﹣2m)、B(m,1),则△OAB的面积是( )
A.3 B. C. D.
50.(2分)(2022 攀枝花)如图,正比例函数y=k1x与反比例函数y=的图象交于A(1,m)、B两点,当k1x≤时,x的取值范围是( )
A.﹣1≤x<0或x≥1 B.x≤﹣1或0<x≤1
C.x≤﹣1或x≥1 D.﹣1≤x<0或0<x≤1
51.(2分)(2022 朝阳)如图,正比例函数y=ax(a为常数,且a≠0)和反比例函数y=(k为常数,且k≠0)的图象相交于A(﹣2,m)和B两点,则不等式ax>的解集为( )
A.x<﹣2或x>2 B.﹣2<x<2
C.﹣2<x<0或x>2 D.x<﹣2或0<x<2
52.(2分)(2022 怀化)如图,直线AB交x轴于点C,交反比例函数y=(a>1)的图象于A、B两点,过点B作BD⊥y轴,垂足为点D,若S△BCD=5,则a的值为( )
A.8 B.9 C.10 D.11
53.(2分)(2021 无锡)在平面直角坐标系中,O为坐标原点,点A(a,2)是反比例函数的图象上的点,连接AO并延长与反比例函数图象交于另一点B,将直线AB向下平移,与反比例函数的图象交于C、D两点.若△ABC的面积为5,则向下平移的距离是( )
A.3 B.5 C.4 D.
54.(2分)(2022 荆州)如图是同一直角坐标系中函数y1=2x和y2=的图象.观察图象可得不等式2x>的解集为( )
A.﹣1<x<1 B.x<﹣1或x>1
C.x<﹣1或0<x<1 D.﹣1<x<0或x>1
55.(2分)(2021 梧州)如图,在同一平面直角坐标系中,直线y=t(t为常数)与反比例函数y1=,y2=﹣的图象分别交于点A,B,连接OA,OB,则△OAB的面积为( )
A.5t B. C. D.5
56.(2分)(2022 内江)如图,在平面直角坐标系中,点M为x轴正半轴上一点,过点M的直线l∥y轴,且直线l分别与反比例函数y=和y=的图象交于P、Q两点.若S△POQ=15,则k的值为( )
A.38 B.22 C.﹣7 D.﹣22
57.(2分)(2021 南通)平面直角坐标系xOy中,直线y=2x与双曲线y=(k>2)相交于A,B两点,其中点A在第一象限.设M(m,2)为双曲线y=(k>2)上一点,直线AM,BM分别交y轴于C,D两点,则OC﹣OD的值为( )
A.2 B.4 C.6 D.8
58.(2分)(2022 宜昌)已知经过闭合电路的电流I(单位:A)与电路的电阻R(单位:Ω)是反比例函数关系.根据下表判断a和b的大小关系为( )
I/A 5 … a … … … b … 1
R/Ω 20 30 40 50 60 70 80 90 100
A.a>b B.a≥b C.a<b D.a≤b
59.(2分)(2022 宁夏)在显示汽车油箱内油量的装置模拟示意图中,电压U一定时,油箱中浮子随油面下降而落下,带动滑杆使滑动变阻器滑片向上移动,从而改变电路中的电流,电流表的示数对应油量体积,把电流表刻度改为相应油量体积数,由此知道油箱里剩余油量.在不考虑其他因素的条件下,油箱中油的体积V与电路中总电阻R总(R总=R+R0)是反比例关系,电流I与R总也是反比例关系,则I与V的函数关系是( )
A.反比例函数 B.正比例函数
C.二次函数 D.以上答案都不对
60.(2分)(2022 丽水)已知电灯电路两端的电压U为220V,通过灯泡的电流强度I(A)的最大限度不得超过0.11A.设选用灯泡的电阻为R(Ω),下列说法正确的是( )
A.R至少2000Ω B.R至多2000Ω C.R至少24.2Ω D.R至多24.2Ω
【真题汇编】2023年中考数学备考之反比例函数(选择题60题)
参考答案与试题解析
一.选择题(共60小题,满分120分,每小题2分)
1.(2分)(2022 襄阳)二次函数y=ax2+bx+c的图象如图所示,则一次函数y=bx+c和反比例函数y=在同一平面直角坐标系中的图象可能是( )
A. B.
C. D.
【解析】解:∵二次函数图象开口方向向下,
∴a<0,
∵对称轴为直线x=﹣>0,
∴b>0,
∵与y轴的负半轴相交,
∴c<0,
∴y=bx+c的图象经过第一、三、四象限,
反比例函数y=图象在第二四象限,
只有D选项图象符合.
故选:D.
2.(2分)(2022 西藏)在同一平面直角坐标系中,函数y=ax+b与y=(其中a,b是常数,ab≠0)的大致图象是( )
A. B.
C. D.
【解析】解:若a>0,b>0,
则y=ax+b经过一、二、三象限,反比例函数y=(ab≠0)位于一、三象限,
若a>0,b<0,
则y=ax+b经过一、三、四象限,反比例函数数y=(ab≠0)位于二、四象限,
若a<0,b>0,
则y=ax+b经过一、二、四象限,反比例函数y=(ab≠0)位于二、四象限,
若a<0,b<0,
则y=ax+b经过二、三、四象限,反比例函数y=(ab≠0)位于一、三象限,
故选:A.
3.(2分)(2022 张家界)在同一平面直角坐标系中,函数y=kx+1(k≠0)和y=(k≠0)的图象大致是( )
A. B.
C. D.
【解析】解:当k>0时,一次函数y=kx+1经过第一、二、三象限,反比例函数y=位于第一、三象限;
当k<0时,一次函数y=kx+1经过第一、二、四象限,反比例函数y=位于第二、四象限;
故选:D.
4.(2分)(2022 绥化)已知二次函数y=ax2+bx+c的部分函数图象如图所示,则一次函数y=ax+b2﹣4ac与反比例函数y=在同一平面直角坐标系中的图象大致是( )
A. B.
C. D.
【解析】解:∵二次函数y=ax2+bx+c的部分函数图象开口向上,
∴a>0,
∵二次函数y=ax2+bx+c的部分函数图象顶点在x轴下方,开口向上,
∴二次函数y=ax2+bx+c的图象与x轴有两个交点,b2﹣4ac>0,
∴一次函数y=ax+b2﹣4ac的图象位于第一,二,三象限,
由二次函数y=ax2+bx+c的部分函数图象可知,点(2,4a+2b+c)在x轴上方,
∴4a+2b+c>0,
∴y=的图象位于第一,三象限,
据此可知,符合题意的是B,
故选:B.
5.(2分)(2022 贺州)已知一次函数y=kx+b的图象如图所示,则y=﹣kx+b与y=的图象为( )
A. B.
C. D.
【解析】解:根据一次函数y=kx+b的图象位置,可判断k>0、b>0.
所以﹣k<0.
再根据一次函数和反比例函数的图像和性质,
故选:A.
6.(2分)(2022 滨州)在同一平面直角坐标系中,函数y=kx+1与y=﹣(k为常数且k≠0)的图象大致是( )
A. B.
C. D.
【解析】解:当k>0时,则﹣k<0,一次函数y=kx+1图象经过第一、二、三象限,反比例函数图象在第二、四象限,所以A选项正确,C选项错误;
当k<0时,一次函数y=kx+1图象经过第一、二,四象限,所以B、D选项错误.
故选:A.
7.(2分)(2021 遵义)已知反比例函数y=(k≠0)的图象如图所示,则一次函数y=kx+2的图象经过( )
A.第一、二、三象限 B.第一、三、四象限
C.第一、二、四象限 D.第二、三、四象限
【解析】解:由反比例函数图象经过二、四象限,可知,k<0,
∴y=kx+2的图象经过一、二、四象限.
故选:C.
8.(2分)(2022 黔西南州)在平面直角坐标系中,反比例函数y=(k≠0)的图象如图所示,则一次函数y=kx+2的图象经过的象限是( )
A.一、二、三 B.一、二、四 C.一、三、四 D.二、三、四
【解析】解:由图可知:k<0,
∴一次函数y=kx+2的图象经过的象限是一、二、四.
故选:B.
9.(2分)(2022 上海)已知反比例函数y=(k≠0),且在各自象限内,y随x的增大而增大,则下列点可能在这个函数图象上的为( )
A.(2,3) B.(﹣2,3) C.(3,0) D.(﹣3,0)
【解析】解:因为反比例函数y=(k≠0),且在各自象限内,y随x的增大而增大,
所以k<0,
A.2×3=6>0,故本选项不符合题意;
B.﹣2×3=﹣6<0,故本选项符合题意;
C.3×0=0,故本选项不符合题意;
D.﹣3×0=0,故本选项不符合题意;
故选:B.
10.(2分)(2022 广东)点(1,y1),(2,y2),(3,y3),(4,y4)在反比例函数y=图象上,则y1,y2,y3,y4中最小的是( )
A.y1 B.y2 C.y3 D.y4
【解析】解:∵k=4>0,
∴在第一象限内,y随x的增大而减小,
∵(1,y1),(2,y2),(3,y3),(4,y4)在反比例函数y=图象上,且1<2<3<4,
∴y4最小.
故选:D.
11.(2分)(2021 黔西南州)对于反比例函数y=,下列说法错误的是( )
A.图象经过点(1,﹣5)
B.图象位于第二、第四象限
C.当x<0时,y随x的增大而减小
D.当x>0时,y随x的增大而增大
【解析】解:∵反比例函数y=,
∴当x=1时,y=﹣=﹣5,故选项A不符合题意;
k=﹣5,故该函数图象位于第二、四象限,故选项B不符合题意;
当x<0,y随x的增大而增大,故选项C符合题意;
当x>0时,y随x的增大而增大,故选项D不符合题意;
故选:C.
12.(2分)(2022 荆门)如图,点A,C为函数y=(x<0)图象上的两点,过A,C分别作AB⊥x轴,CD⊥x轴,垂足分别为B,D,连接OA,AC,OC,线段OC交AB于点E,且点E恰好为OC的中点.当△AEC的面积为时,k的值为( )
A.﹣1 B.﹣2 C.﹣3 D.﹣4
【解析】解:∵点E为OC的中点,
∴△AEO的面积=△AEC的面积=,
∵点A,C为函数y=(x<0)图象上的两点,
∴S△ABO=S△CDO,
∴S四边形CDBE=S△AEO=,
∵EB∥CD,
∴△OEB∽△OCD,
∴=()2,
∴S△OCD=1,
则xy=﹣1,
∴k=xy=﹣2.
故选:B.
13.(2分)(2021 德州)小红同学在研究函数y=|x|+的图象时,发现有如下结论:①该函数有最小值;②该函数图象与坐标轴无交点;③当x>0时,y随x的增大而增大;④该函数图象关于y轴对称;⑤直线y=8与该函数图象有两个交点,则上述结论中正确的个数为( )
A.2个 B.3个 C.4个 D.5个
【解析】解:列表:
x … ﹣4 ﹣3 ﹣2 ﹣1 1 2 3 4 …
y … 5 4 5 5 4 5 …
画出函数图象如图,
观察图象:
①该函数有最小值,符合题意;
②该函数图象与坐标轴无交点,符合题意;
③当x>0时,y随x的增大而增大,不合题意;
④该函数图象关于y轴对称,符合题意;
⑤令|x|+=8,整理得x2﹣8x+4=0或x2+8x+4=0,
∵Δ=82﹣4×1×4>0,
∴两个方程均有两个不相等的实数根,即共有四个根,且这四个根互不相等.
∴直线y=8与该函数图象有四个交点,不符合题意,
综上,以上结论正确的有:①②④,
故选:B.
14.(2分)(2021 济南)反比例函数y=(k≠0)图象的两个分支分别位于第一、三象限,则一次函数y=kx﹣k的图象大致是( )
A. B. C. D.
【解析】解:∵反比例函数y=(k≠0)图象的两个分支分别位于第一、三象限,
∴k>0,
∴﹣k<0,
∴一次函数y=kx﹣k的图象图象经过第一、三、四象限,
故选:D.
15.(2分)(2021 阜新)已知点A(x1,y1),B(x2,y2)都在反比例函数y=﹣的图象上,且x1<0<x2,则y1,y2的关系一定成立的是( )
A.y1>y2 B.y1<y2 C.y1+y2=0 D.y1﹣y2=0
【解析】解:∵反比例函数y=﹣中k=﹣1<0,
∴函数图象的两个分支分别位于二、四象限,且在每一象限内,y随x的增大而增大.
∵x1<0<x2,
∴A在第二象限,B在第四象限,
∴y1>0,y2<0,
∴y1>y2.
故选:A.
16.(2分)(2021 湘西州)如图所示,小英同学根据学习函数的经验,自主尝试在平面直角坐标系中画出了一个解析式为y=的函数图象.根据这个函数的图象,下列说法正确的是( )
A.图象与x轴没有交点
B.当x>0时,y>0
C.图象与y轴的交点是(0,﹣)
D.y随x的增大而减小
【解析】解:A.由图象可知,图象与x轴没有交点,故说法正确;
B.由图象可知,当0<x<1时,y<0,当x>1时,y>0,故说法错误;
C.当x=0时,函数值为﹣2,故图象与y轴的交点是(0,﹣2),故说法错误;
D.当x>1时,y随x的增大而减小,当x<1时,y随x的增大而减小,故说法错误.
故选:A.
17.(2分)(2021 兰州)如图,点A在反比例函数y=(x>0)图象上,AB⊥x轴于点B,C是OB的中点,连接AO,AC,若△AOC的面积为2,则k=( )
A.4 B.8 C.12 D.16
【解析】解:∵C是OB的中点,△AOC的面积为2,
∴△AOB的面积为4,
∵AB⊥x轴,
∴AB OB=4,
∴AB OB=8,
∴k=8.
故选:B.
18.(2分)(2022 日照)如图,矩形OABC与反比例函数y1=(k1是非零常数,x>0)的图象交于点M,N,与反比例函数y2=(k2是非零常数,x>0)的图象交于点B,连接OM,ON.若四边形OMBN的面积为3,则k1﹣k2=( )
A.3 B.﹣3 C. D.
【解析】解:∵y1、y2的图象均在第一象限,
∴k1>0,k2>0,
∵点M、N均在反比例函数y1=(k1是非零常数,x>0)的图象上,
∴S△OAM=S△OCN=k1,
∵矩形OABC的顶点B在反比例函数y2=(k2是非零常数,x>0)的图象上,
∴S矩形OABC=k2,
∴S四边形OMBN=S矩形OABC﹣S△OAM﹣S△OCN=3,
∴k2﹣k1=3,
∴k1﹣k2=﹣3,
故选:B.
19.(2分)(2022 牡丹江)如图,等边三角形OAB,点B在x轴正半轴上,S△OAB=4,若反比例函数y=(k≠0)图象的一支经过点A,则k的值是( )
A. B. C. D.
【解析】解:如图,过点A作AC⊥OB于点C,
∵△OAB是正三角形,
∴OC=BC,
∴S△AOC=S△AOB=2=|k|,
又∵k>0,
∴k=4,
故选:D.
20.(2分)(2022 通辽)如图,点D是 OABC内一点,AD与x轴平行,BD与y轴平行,BD=,∠BDC=120°,S△BCD=,若反比例函数y=(x<0)的图象经过C,D两点,则k的值是( )
A.﹣6 B.﹣6 C.﹣12 D.﹣12
【解析】解:过点C作CE⊥y轴,延长BD交CE于点F,
∵四边形OABC为平行四边形,
∴AB∥OC,AB=OC,
∴∠COE=∠1,
∵BD与y轴平行,
∴∠1=∠ABD,∠ADB=90°,
∴∠COE=∠ABD,
在△COE和△ABD中,
,
∴△COE≌△ABD(AAS),
∴OE=BD=,
∵S△BDC=BD CF=,
∴CF=9,
∵∠BDC=120°,
∴∠CDF=60°,
∴DF=3,
点D的纵坐标为4,
设C(m,),则D(m+9,4),
∵反比例函数y=(x<0)的图象经过C,D两点,
∴k=m=4(m+9),
∴m=﹣12,
∴k=﹣12,
故选:C.
21.(2分)(2022 郴州)如图,在函数y=(x>0)的图象上任取一点A,过点A作y轴的垂线交函数y=﹣(x<0)的图象于点B,连接OA,OB,则△AOB的面积是( )
A.3 B.5 C.6 D.10
【解析】解:∵点A在函数y=(x>0)的图象上,
∴S△AOC=×2=1,
又∵点B在反比例函数y=﹣(x<0)的图象上,
∴S△BOC=×8=4,
∴S△AOB=S△AOC+S△BOC
=1+4
=5,
故选:B.
22.(2分)(2021 牡丹江)如图,矩形OABC的面积为36,它的对角线OB与双曲线y=相交于点D,且OD:OB=2:3,则k的值为( )
A.12 B.﹣12 C.16 D.﹣16
【解析】解:方法一、如图,连接CD,过点D作DE⊥CO于E,
∵矩形OABC的面积为36,
∴S△BCO=18,
∵OD:OB=2:3,
∴S△CDO==12,
∵DE⊥CO,BC⊥CO,
∴DE∥BC,
∴,
∴S△DEO==8,
∵双曲线y=图象过点D,
∴=8,
又∵双曲线y=图象在第二象限,
∴k<0,
∴k=﹣16,
方法二、∵矩形OABC的面积为36,
∴S△BCO=18,
∵DE∥BC,
∴=()2=,
∴S△DEO=18×=8,
∵双曲线y=图象过点D,
∴=8,
又∵双曲线y=图象在第二象限,
∴k<0,
∴k=﹣16,
故选:D.
23.(2分)(2022 黑龙江)如图,在平面直角坐标系中,点O为坐标原点,平行四边形OBAD的顶点B在反比例函数y=的图象上,顶点A在反比例函数y=的图象上,顶点D在x轴的负半轴上.若平行四边形OBAD的面积是5,则k的值是( )
A.2 B.1 C.﹣1 D.﹣2
【解析】解:设B(a,),
∵四边形OBAD是平行四边形,
∴AB∥DO,
∴A(,),
∴AB=a﹣,
∵平行四边形OBAD的面积是5,
∴(a﹣)=5,
解得k=﹣2,
故选:D.
24.(2分)(2022 十堰)如图,正方形ABCD的顶点分别在反比例函数y=(k1>0)和y=(k2>0)的图象上.若BD∥y轴,点D的横坐标为3,则k1+k2=( )
A.36 B.18 C.12 D.9
【解析】解:连接AC交BD于E,延长BD交x轴于F,连接OD、OB,如图:
∵四边形ABCD是正方形,
∴AE=BE=CE=DE,
设AE=BE=CE=DE=m,D(3,a),
∵BD∥y轴,
∴B(3,a+2m),A(3+m,a+m),
∵A,B都在反比例函数y=(k1>0)的图象上,
∴k1=3(a+2m)=(3+m)(a+m),
∵m≠0,
∴m=3﹣a,
∴B(3,6﹣a),
∵B(3,6﹣a)在反比例函数y=(k1>0)的图象上,D(3,a)在y=(k2>0)的图象上,
∴k1=3(6﹣a)=18﹣3a,k2=3a,
∴k1+k2=18﹣3a+3a=18;
故选:B.
25.(2分)(2021 兰州)如图,点A在反比例函数y=(x>0)的图象上,AB⊥x轴于点B,C是OB的中点,连接AO,AC,若△AOC的面积为4,则k=( )
A.16 B.12 C.8 D.4
【解析】解:∵C是OB的中点,△AOC的面积为4,
∴△AOB的面积为8,
设A(a,b)
∵AB⊥x轴于点B,
∴ab=16,
∵点A在反比例函数y=(x>0)的图象上,
∴k=16.
故选:A.
26.(2分)(2021 西藏)如图.在平面直角坐标系中,△AOB的面积为,BA垂直x轴于点A,OB与双曲线y=相交于点C,且BC:OC=1:2.则k的值为( )
A.﹣3 B.﹣ C.3 D.
【解析】解:过C作CD⊥x轴于D,
∵=,
∴=,
∵BA⊥x轴,
∴CD∥AB,
∴△DOC∽△AOB,
∴=()2=()2=,
∵S△AOB=,
∴S△DOC=S△AOB=×=,
∵双曲线y=在第二象限,
∴k=﹣2×=﹣3,
故选:A.
27.(2分)(2021 丹东)如图,点A在双曲线y1=(x>0)上,点B在双曲线y2=(x<0)上,AB∥x轴,点C是x轴上一点,连接AC、BC,若△ABC的面积是6,则k的值( )
A.﹣6 B.﹣8 C.﹣10 D.﹣12
【解析】解:如图,连接OA,OB,AB与y轴交于点M,
∵AB∥x轴,点A双在曲线y1=(x>0)上,点B在双曲线y2=(x<0)上,
∴S△AOM=×|2|=1,S△BOM=×|k|=﹣k,
∵S△ABC=S△AOB=6,
∴1﹣k=6,
∴k=﹣10.
故选:C.
28.(2分)(2021 黑龙江)如图,在平面直角坐标系中,矩形ABCD的顶点A在双曲线y=﹣(x<0)上,点C,D在y轴的正半轴上,点E在BC上,CE=2BE,连接DE并延长,交x轴于点F,连接CF,则△FCD的面积为( )
A.2 B. C.1 D.
【解析】解:根据题意,设A(n,﹣),D(0,﹣),
设OC=m,则C(0,m),CD=﹣﹣m,
∴B(n,m),BC=﹣n,
∵CE=2BE,
∴CE=BC=﹣n,
∴E(n,m),
由题知BC∥FO,
∴∠DEC=∠DFO,∠DCE=∠DOF,
∴△DEC∽△DFO,
∴=,
即=,
∴FO=,
∴S△FCD=FO CD=×(﹣﹣m)=1,
故选:C.
29.(2分)(2021 淄博)如图,在平面直角坐标系中,四边形AOBD的边OB与x轴的正半轴重合,AD∥OB,DB⊥x轴,对角线AB,OD交于点M.已知AD:OB=2:3,△AMD的面积为4.若反比例函数y=的图象恰好经过点M,则k的值为( )
A. B. C. D.12
【解析】解:过点M作MH⊥OB于H.
∵AD∥OB,
∴△ADM∽△BOM,
∴=()2=,
∵S△ADM=4,
∴S△BOM=9,
∵DB⊥OB,MH⊥OB,
∴MH∥DB,
∴===,
∴OH=OB,
∴S△MOH=×S△OBM=,
∵=,
∴k=,
故选:B.
30.(2分)(2021 兴安盟)点(﹣5,y1),(﹣3,y2),(3,y3)都在反比例函数y=(k>0)的图象上,则( )
A.y1>y2>y3 B.y3>y1>y2 C.y2>y1>y3 D.y1>y3>y2
【解析】解:∵反比例函数y=中k>0,
∴函数图象的两个分支分别位于一、三象限,且在每一象限内y随x的增大而减小.
∵﹣5<﹣3<0,
∴0>y1>y2,
∵3>0,
∴y3>0,
∴y3>y1>y2,
故选:B.
31.(2分)(2021 德州)已知点A(x1,y1),B(x2,y2),C(x3,y3)都在反比例函数y=(a是常数)的图象上,且y1<y2<0<y3,则x1,x2,x3的大小关系为( )
A.x2>x1>x3 B.x1>x2>x3 C.x3>x2>x1 D.x3>x1>x2
【解析】解:∵a2+1>0,
∴反比例函数y=(a是常数)的图象在一、三象限,
如图所示,当y1<y2<0<y3时,x3>0>x1>x2,
故选:D.
32.(2分)(2022 阜新)已知反比例函数y=(k≠0)的图象经过点(﹣2,4),那么该反比例函数图象也一定经过点( )
A.(4,2) B.(1,8) C.(﹣1,8) D.(﹣1,﹣8)
【解析】解:∵反比例函数y=(k≠0)的图象经过点(﹣2,4),
∴k=﹣2×4=﹣8,
A、∵4×2=8≠﹣8,∴此点不在反比例函数的图象上,故本选项错误;
B、∵1×8=8≠﹣8,∴此点不在反比例函数的图象上,故本选项错误;
C、﹣1×8=﹣8,∴此点在反比例函数的图象上,故本选项正确;
D、(﹣1)×(﹣8)=8≠﹣8,∴此点不在反比例函数的图象上,故本选项错误.
故选:C.
33.(2分)(2022 襄阳)若点A(﹣2,y1),B(﹣1,y2)都在反比例函数y=的图象上,则y1,y2的大小关系是( )
A.y1<y2 B.y1=y2 C.y1>y2 D.不能确定
【解析】解:∵点A(﹣2,y1),B(﹣1,y2)都在反比例函数y=的图象上,k=2>0,
∴在每个象限内y随x的增大而减小,
∵﹣2<﹣1,
∴y1>y2,
故选:C.
34.(2分)(2022 枣庄)如图,正方形ABCD的边长为5,点A的坐标为(4,0),点B在y轴上,若反比例函数y=(k≠0)的图象过点C,则k的值为( )
A.4 B.﹣4 C.﹣3 D.3
【解析】解:如图,过点C作CE⊥y轴于E,在正方形ABCD中,AB=BC,∠ABC=90°,
∴∠ABO+∠CBE=90°,
∵∠OAB+∠ABO=90°,
∴∠OAB=∠CBE,
∵点A的坐标为(4,0),
∴OA=4,
∵AB=5,
∴OB==3,
在△ABO和△BCE中,
,
∴△ABO≌△BCE(AAS),
∴OA=BE=4,CE=OB=3,
∴OE=BE﹣OB=4﹣3=1,
∴点C的坐标为(﹣3,1),
∵反比例函数y=(k≠0)的图象过点C,
∴k=xy=﹣3×1=﹣3,
故选:C.
35.(2分)(2022 长春)如图,在平面直角坐标系中,点P在反比例函数y=(k>0,x>0)的图象上,其纵坐标为2,过点P作PQ∥y轴,交x轴于点Q,将线段QP绕点Q顺时针旋转60°得到线段QM.若点M也在该反比例函数的图象上,则k的值为( )
A. B. C. D.4
【解析】解:作MN⊥x轴于N,
∵P在反比例函数y=(k>0,x>0)的图象上,其纵坐标为2,过点P作PQ∥y轴,交x轴于点Q,
∴P(,2),
∴PQ=2,
∵将线段QP绕点Q顺时针旋转60°得到线段QM.
∴QM=QP=2,∠PQM=60°,
∴∠MQN=90°﹣60°=30°,
∴MN=QM=1,
∴QN==,
∴M(+,1),
∵点M也在该反比例函数的图象上,
∴k=+,
解得k=2,
故选:C.
36.(2分)(2022 贵阳)如图,在平面直角坐标系中有P,Q,M,N四个点,其中恰有三点在反比例函数y=(k>0)的图象上.根据图中四点的位置,判断这四个点中不在函数y=的图象上的点是( )
A.点P B.点Q C.点M D.点N
通过观察发现,点P、Q、N可能在图象上,点M不在图象上,
故选:C.
37.(2分)(2022 娄底)在平面直角坐标系中,O为坐标原点,已知点P(m,1)、Q(1,m)(m>0且m≠1),过点P、Q的直线与两坐标轴相交于A、B两点,连接OP、OQ,则下列结论中成立的有( )
①点P、Q在反比例函数y=的图象上;
②△AOB为等腰直角三角形;
③0°<∠POQ<90°;
④∠POQ的值随m的增大而增大.
A.②③④ B.①③④ C.①②④ D.①②③
【解析】解:∵点P(m,1)、Q(1,m)(m>0且m≠1),则m 1=1 m=m,
∴点P、Q在反比例函数y=的图象上,故①正确;
设直线PQ为y=kx+b,则,解得,
∴直线PQ为y=﹣x+m+1,
当y=0时,x=m+1;当x=0时,y=m+1,
∴A(m+1,0),B(0,m+1),
∴OA=OB,
∵∠AOB=90°,
∴△AOB为等腰直角三角形,故②正确;
∵点P(m,1)、Q(1,m)(m>0且m≠1),
∴P、Q都在第一象限,
∴0°<∠POQ<90°,故③正确;
∵直线OP为y=x,直线OQ为y=mx,
∴当0<m<1时,∠POQ的值随m的增大而减小,当m>1时,∠POQ的值随m的增大而增大,
故④错误;
故选:D.
38.(2分)(2022 天津)若点A(x1,2),B(x2,﹣1),C(x3,4)都在反比例函数y=的图象上,则x1,x2,x3的大小关系是( )
A.x1<x2<x3 B.x2<x3<x1 C.x1<x3<x2 D.x2<x1<x3
【解析】解:点A(x1,2),B(x2,﹣1),C(x3,4)都在反比例函数y=的图象上,
∴x1==4,x2==﹣8,x3==2.
∴x2<x3<x1,
故选:B.
39.(2分)(2021 内江)如图,菱形ABCD的顶点分别在反比例函数y=和y=的图象上,若∠BCD=60°,则的值为( )
A. B. C. D.
【解析】解:连接AC、BD,
∵四边形ABCD是菱形,
∴AC⊥BD,
∵菱形ABCD的顶点分别在反比例函数y=和y=的图象上,
∴A与C、B与D关于原点对称,
∴AC、BD经过点O,
∴∠BOC=90°,
∵∠BCO=∠BCD=30°,
∴tan30°==,
作BM⊥x轴于M,CN⊥x轴于N,
∵∠BOM+∠NOC=90°=∠NOC+∠NCO,
∴∠BOM=∠NCO,
∵∠OMB=∠CNO=90°,
∴△OMB∽△CNO,
∴=()2,
∴=,
∴=﹣,
故选:D.
40.(2分)(2021 朝阳)如图,O是坐标原点,点B在x轴上,在△OAB中,AO=AB=5,OB=6,点A在反比例函数y=(k≠0)图象上,则k的值( )
A.﹣12 B.﹣15 C.﹣20 D.﹣30
【解析】解:过A点作AC⊥OB,
∵AO=AB,AC⊥OB,OB=6,
∴OC=BC=3,
在Rt△AOC中,OA=5,
∵AC=,
∴A(﹣3,4),
把A(﹣3,4)代入y=,可得k=﹣12,
故选:A.
41.(2分)(2021 大连)下列说法正确的是( )
①反比例函数y=中自变量x的取值范围是x≠0;
②点P(﹣3,2)在反比例函数y=﹣的图象上;
③反比例函数y=的图象,在每一个象限内,y随x的增大而增大.
A.①② B.①③ C.②③ D.①②③
【解析】解:①反比例函数y=中自变量x的取值范围是x≠0,故说法正确;
②因为﹣3×2=﹣6,故说法正确;
③因为k=3>0,反比例函数y=的图象,在每一个象限内,y随x的增大而减小,故说法错误;
故选:A.
42.(2分)(2022 海南)若反比例函数y=(k≠0)的图象经过点(2,﹣3),则它的图象也一定经过的点是( )
A.(﹣2,﹣3) B.(﹣3,﹣2) C.(1,﹣6) D.(6,1)
【解析】解:∵反比例函数y=(k≠0)的图象经过点(2,﹣3),
∴k=2×(﹣3)=﹣6,
A、﹣2×(﹣3)=6≠﹣6,故A不正确,不符合题意;
B、(﹣3)×(﹣2)=6≠﹣6,故B不正确,不符合题意;
C、1×(﹣6)=﹣6,故C正确,符合题意,
D、6×1=6≠﹣6,故D不正确,不符合题意.
故选:C.
43.(2分)(2022 武汉)已知点A(x1,y1),B(x2,y2)在反比例函数y=的图象上,且x1<0<x2,则下列结论一定正确的是( )
A.y1+y2<0 B.y1+y2>0 C.y1<y2 D.y1>y2
【解析】解:∵反比例函数y=中的6>0,
∴该双曲线位于第一、三象限,且在每一象限内y随x的增大而减小,
∵点A(x1,y1),B(x2,y2)在反比例函数y=的图象上,且x1<0<x2,
∴点A位于第三象限,点B位于第一象限,
∴y1<y2.
故选:C.
44.(2分)(2022 宿迁)如图,点A在反比例函数y=(x>0)的图象上,以OA为一边作等腰直角三角形OAB,其中∠OAB=90°,AO=AB,则线段OB长的最小值是( )
A.1 B. C.2 D.4
【解析】解:∵三角形OAB是等腰直角三角形,
∴当OB最小时,OA最小,
设A点坐标为(a,),
∴OA=,
∵≥0,
即:﹣4≥0,
∴≥4,
∵≥0,
两边同时开平方得:a﹣=0,
∴当a=时,OA有最小值,
解得a1=,a2=﹣(舍去),
∴A点坐标为(,),
∴OA=2,
∵三角形OAB是等腰直角三角形,OB为斜边,
∴OB=OA=2.
故选:C.
45.(2分)(2021 益阳)正比例函数y=2x与反比例函数y=的图象或性质的共有特征之一是( )
A.函数值y随x的增大而增大
B.图象在第一、三象限都有分布
C.图象与坐标轴有交点
D.图象经过点(2,1)
【解析】解:∵对于正比例函数y=2x,2>0,函数值y随x的增大而增大,
对于反比例函数y=,2>0,双曲线在每一象限内函数值y随x的增大而减小,
∴A选项不符合题意;
∵对于正比例函数y=2x,2>0,直线y=2x经过第一、三象限,
对于反比例函数y=,2>0,双曲线的两个分支在第一、三象限,
∴B选项符合题意;
∵对于正比例函数y=2x,它的图象经过原点,
对于反比例函数y=,它的图象与坐标轴没有交点,
∴C选项不符合题意;
∵当x=2,y=2×2=4≠1
∴正比例函数y=2x的图象不经过点(2,1).
∵当x=2时,y=,
∴反比例函数y=的图象经过(2,1),
∴D选项不符合题意.
综上,正确选项为:B.
故选:B.
46.(2分)(2021 滨州)如图,在△OAB中,∠BOA=45°,点C为边AB上一点,且BC=2AC.如果函数y=(x>0)的图象经过点B和点C,那么用下列坐标表示的点,在直线BC上的是( )
A.(﹣2019,674) B.(﹣2020,675)
C.(2021,﹣669) D.(2022,﹣670)
【解析】解:作BD⊥OA,CE⊥OA,
∵∠BOA=45°,
∴BD=OD,
设B(a,a),
∴,
∴a=3或a=﹣3(舍去),
∴BD=OD=3,
B(3,3),
∵BC=2AC.
∴AB=3AC,
∵BD⊥OA,CE⊥OA,
∴BD∥CE,
.∴△ABD∽△ACE
∵=3,
∴,
∴CE=1,
∵图象经过点C,
∴,
∴x=9,
C(9,1)
设BC的解析式为y=kx+b,
,
解得,
∴x+4,
当x=﹣2019时,y=677,
当x=﹣2020时,y=677,
当x=2021时,y=﹣669,
当x=2022时,y=﹣670,
故选:D.
47.(2分)(2021 广州)在平面直角坐标系xOy中,矩形OABC的顶点A在函数y=(x>0)的图象上,顶点C在函数y=﹣(x<0)的图象上,若顶点B的横坐标为﹣,则点A的坐标为( )
A.(,2) B.(,) C.(2,) D.(,)
【解析】解:如图,作AD⊥x轴于点D,CE⊥x轴于点E,
∵四边形OABC是矩形,
∴∠AOC=90°,
∴∠AOD+∠COE=90°,
∵∠AOD+∠OAD=90°,
∴∠COE=∠OAD,
∵∠CEO=∠ODA,
∴△COE∽△OAD,
∴=()2,,
∵S△COE=×|﹣4|=2,S△AOD==,
∴=()2,
∴=2,
∴=,
∴OE=2AD,CE=2OD,
设A(m,)(m>0),
∴C(﹣,2m),
∴OE=0﹣(﹣)=,
∵点B的横坐标为﹣,
∴m﹣(﹣)=,
整理得2m2+7m﹣4=0,
∴m1=,m2=﹣4(不符合题意,舍去),
经检验,m=是方程的解,
∴A(,2),
故选:A.
48.(2分)(2022 东营)如图,一次函数y1=k1x+b与反比例函数y2=的图象相交于A,B两点,点A的横坐标为2,点B的横坐标为﹣1,则不等式k1x+b<的解集是( )
A.﹣1<x<0或x>2 B.x<﹣1或0<x<2
C.x<﹣1或x>2 D.﹣1<x<2
【解析】解:观察函数图象可知,当﹣1<x<0或x>2时,一次函数y1=k1x+b的图象在反比例函数y2=的图象的下方,
∴不等式k1x+b<的解集为:﹣1<x<0或x>2,
故选:A.
49.(2分)(2022 无锡)一次函数y=mx+n的图象与反比例函数y=的图象交于点A、B,其中点A、B的坐标为A(﹣,﹣2m)、B(m,1),则△OAB的面积是( )
A.3 B. C. D.
【解析】解:∵点A(﹣,﹣2m)在反比例函数y=上,
∴﹣2m=,
解得:m=2,
∴点A的坐标为:(﹣,﹣4),点B的坐标为(2,1),
∴S△OAB=××5﹣××4﹣×2×1﹣×1=,
故选:D.
50.(2分)(2022 攀枝花)如图,正比例函数y=k1x与反比例函数y=的图象交于A(1,m)、B两点,当k1x≤时,x的取值范围是( )
A.﹣1≤x<0或x≥1 B.x≤﹣1或0<x≤1
C.x≤﹣1或x≥1 D.﹣1≤x<0或0<x≤1
【解析】解:∵正比例函数y=k1x与反比例函数y=的图象交于A(1,m)、B两点,
∴B(﹣1,﹣m),
由图象可知,当k1x≤时,x的取值范围是﹣1≤x<0或x≥1,
故选:A.
51.(2分)(2022 朝阳)如图,正比例函数y=ax(a为常数,且a≠0)和反比例函数y=(k为常数,且k≠0)的图象相交于A(﹣2,m)和B两点,则不等式ax>的解集为( )
A.x<﹣2或x>2 B.﹣2<x<2
C.﹣2<x<0或x>2 D.x<﹣2或0<x<2
【解析】解:∵正比例函数y=ax(a为常数,且a≠0)和反比例函数y=(k为常数,且k≠0)的图象相交于A(﹣2,m)和B两点,
∴B(2,﹣m),
∴不等式ax>的解集为x<﹣2或0<x<2,
故选:D.
52.(2分)(2022 怀化)如图,直线AB交x轴于点C,交反比例函数y=(a>1)的图象于A、B两点,过点B作BD⊥y轴,垂足为点D,若S△BCD=5,则a的值为( )
A.8 B.9 C.10 D.11
【解析】解:设点B的坐标为(m,),
∵S△BCD=5,且a>1,
∴×m×=5,
解得:a=11,
故选:D.
53.(2分)(2021 无锡)在平面直角坐标系中,O为坐标原点,点A(a,2)是反比例函数的图象上的点,连接AO并延长与反比例函数图象交于另一点B,将直线AB向下平移,与反比例函数的图象交于C、D两点.若△ABC的面积为5,则向下平移的距离是( )
A.3 B.5 C.4 D.
【解析】解:∵点A(a,2)是反比例函数的图象上的点,
∴2a=﹣2,
∴a=﹣1,
∴A(﹣1,2),
∵AB过原点,
∴B(1,﹣2),
∴AB==2,直线AB为y=﹣2x,
过C点作CD⊥AB于D,CE∥x轴交AB于E,
∵S△ABC=CD AB=5,
∴CD===,
设直线AB向左平移m个单位,
∴得y=﹣2(x+m)=﹣2x﹣2m(m>0),
∴CE=m,CD=CE sin∠CED,
作AH⊥y轴于H,
∵CE∥AH,
∴∠CED=∠OAH,
∵sin∠OAH===,
∴CD=m =,
解得m=,
∴﹣2m=﹣5,
∴向下平移的距离是5,
故选:B.
54.(2分)(2022 荆州)如图是同一直角坐标系中函数y1=2x和y2=的图象.观察图象可得不等式2x>的解集为( )
A.﹣1<x<1 B.x<﹣1或x>1
C.x<﹣1或0<x<1 D.﹣1<x<0或x>1
【解析】解:由图象,函数y1=2x和y2=的交点横坐标为﹣1,1,
∴当﹣1<x<0或x>1时,y1>y2,即2x>,
故选:D.
55.(2分)(2021 梧州)如图,在同一平面直角坐标系中,直线y=t(t为常数)与反比例函数y1=,y2=﹣的图象分别交于点A,B,连接OA,OB,则△OAB的面积为( )
A.5t B. C. D.5
【解析】解:如图,设AB交y轴于T.
∵AB⊥y轴,
∴S△OBT=,S△OAT==2,
∴S△AOB=S△OBT+S△OAT=+2=,
故选:C.
56.(2分)(2022 内江)如图,在平面直角坐标系中,点M为x轴正半轴上一点,过点M的直线l∥y轴,且直线l分别与反比例函数y=和y=的图象交于P、Q两点.若S△POQ=15,则k的值为( )
A.38 B.22 C.﹣7 D.﹣22
【解析】解:∵直线l∥y轴,
∴∠OMP=∠OMQ=90°,
∴S△OMP=×8=4,S△OMQ=﹣k.
又S△POQ=15,
∴4﹣k=15,
即k=11,
∴k=﹣22.
故选:D.
57.(2分)(2021 南通)平面直角坐标系xOy中,直线y=2x与双曲线y=(k>2)相交于A,B两点,其中点A在第一象限.设M(m,2)为双曲线y=(k>2)上一点,直线AM,BM分别交y轴于C,D两点,则OC﹣OD的值为( )
A.2 B.4 C.6 D.8
【解析】解:解法一:设A(a,2a),M(m,2),则B(﹣a,﹣2a),
设直线BM的解析式为:y=nx+b,
则,解得:,
∴直线BM的解析式为:y=x+,
∴OD=,
同理得:直线AM的解析式为:y=x+,
∴OC=,
∵a 2a=2m,
∴m=a2,
∴OC﹣OD=﹣=4;
解法二:由题意得:,
解得:,,
∵点A在第一象限,
∴A(,),B(﹣,﹣),
∵M(m,2)为双曲线y=(k>2)上一点,
∴2m=k,
∴m=,
∴M(,2),
如图,过点A作AP⊥y轴于P,过点M作ME⊥y轴于E,过点B作BF⊥y轴于F,
∴∠MED=∠BFD=90°,
∵∠EDM=∠BDF,
∴△EMD∽△FBD,
∴,即==,
∴OD==﹣2,
∵∠CPA=∠CEM=90°,∠ACP=∠ECM,
∴△CPA∽△CEM,
∴,即==,
∴OC===+2,
∴OC﹣OD=+2﹣(﹣2)=4.
解法三:取k=8,如图,则M(4,2),A(2,4),B(﹣2,﹣4),
得AM的解析式为:y=﹣x+6,BM的解析式为:y=x﹣2,
∴OC=6,OD=2,
∴OC﹣OD=6﹣2=4.
故选:B.
58.(2分)(2022 宜昌)已知经过闭合电路的电流I(单位:A)与电路的电阻R(单位:Ω)是反比例函数关系.根据下表判断a和b的大小关系为( )
I/A 5 … a … … … b … 1
R/Ω 20 30 40 50 60 70 80 90 100
A.a>b B.a≥b C.a<b D.a≤b
【解析】解:∵闭合电路的电流I(单位:A)与电路的电阻R(单位:Ω)是反比例函数关系,
∴40a=80b,
∴a=2b,
∴a>b,
故选:A.
59.(2分)(2022 宁夏)在显示汽车油箱内油量的装置模拟示意图中,电压U一定时,油箱中浮子随油面下降而落下,带动滑杆使滑动变阻器滑片向上移动,从而改变电路中的电流,电流表的示数对应油量体积,把电流表刻度改为相应油量体积数,由此知道油箱里剩余油量.在不考虑其他因素的条件下,油箱中油的体积V与电路中总电阻R总(R总=R+R0)是反比例关系,电流I与R总也是反比例关系,则I与V的函数关系是( )
A.反比例函数 B.正比例函数
C.二次函数 D.以上答案都不对
【解析】解:由油箱中油的体积V与电路中总电阻R总是反比例关系,设V R总=k(k为常数),
由电流I与R总是反比例关系,设I R总=k'(k为常数),
∴=,
∴I=V(为常数),
∴I与V的函数关系是正比例函数,
故选:B.
60.(2分)(2022 丽水)已知电灯电路两端的电压U为220V,通过灯泡的电流强度I(A)的最大限度不得超过0.11A.设选用灯泡的电阻为R(Ω),下列说法正确的是( )
A.R至少2000Ω B.R至多2000Ω C.R至少24.2Ω D.R至多24.2Ω
【解析】解:∵电压U一定时,电流强度I(A)与灯泡的电阻为R(Ω)成反比例,
∴I=.
∵已知电灯电路两端的电压U为220V,
∴I=.
∵通过灯泡的电流强度I(A)的最大限度不得超过0.11A,
∴≤0.11,
∴R≥2000.
故选:A.
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
【真题汇编】2023年中考数学备考之反比例函数
1.反比例函数的图象
用描点法画反比例函数的图象,步骤:列表﹣﹣﹣描点﹣﹣﹣连线.
(1)列表取值时,x≠0,因为x=0函数无意义,为了使描出的点具有代表性,可以以“0”为中心,向两边对称式取值,即正、负数各一半,且互为相反数,这样也便于求y值.
(2)由于函数图象的特征还不清楚,所以要尽量多取一些数值,多描一些点,这样便于连线,使画出的图象更精确.
(3)连线时要用平滑的曲线按照自变量从小到大的顺序连接,切忌画成折线.
(4)由于x≠0,k≠0,所以y≠0,函数图象永远不会与x轴、y轴相交,只是无限靠近两坐标轴.
2.反比例函数的性质
反比例函数的性质
(1)反比例函数y=(k≠0)的图象是双曲线;
(2)当k>0,双曲线的两支分别位于第一、第三象限,在每一象限内y随x的增大而减小;
(3)当k<0,双曲线的两支分别位于第二、第四象限,在每一象限内y随x的增大而增大.
注意:反比例函数的图象与坐标轴没有交点.
3.反比例函数系数k的几何意义
比例系数k的几何意义
在反比例函数y=图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.
在反比例函数的图象上任意一点向坐标轴作垂线,这一点和垂足以及坐标原点所构成的三角形的面积是|k|,且保持不变.
4.反比例函数图象上点的坐标特征
反比例函数y=k/x(k为常数,k≠0)的图象是双曲线,
①图象上的点(x,y)的横纵坐标的积是定值k,即xy=k;
②双曲线是关于原点对称的,两个分支上的点也是关于原点对称;
③在y=k/x图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.
5.待定系数法求反比例函数解析式
用待定系数法求反比例函数的解析式要注意:
(1)设出含有待定系数的反比例函数解析式y=(k为常数,k≠0);
(2)把已知条件(自变量与函数的对应值)带入解析式,得到待定系数的方程;
(3)解方程,求出待定系数;
(4)写出解析式.
6.反比例函数与一次函数的交点问题
反比例函数与一次函数的交点问题
(1)求反比例函数与一次函数的交点坐标,把两个函数关系式联立成方程组求解,若方程组有解则两者有交点,方程组无解,则两者无交点.
(2)判断正比例函数y=k1x和反比例函数y=在同一直角坐标系中的交点个数可总结为:
①当k1与k2同号时,正比例函数y=k1x和反比例函数y=在同一直角坐标系中有2个交点;
②当k1与k2异号时,正比例函数y=k1x和反比例函数y=在同一直角坐标系中有0个交点.
7.反比例函数的应用
(1)利用反比例函数解决实际问题
①能把实际的问题转化为数学问题,建立反比例函数的数学模型.②注意在自变量和函数值的取值上的实际意义.③问题中出现的不等关系转化成相等的关系来解,然后在作答中说明.
(2)跨学科的反比例函数应用题
要熟练掌握物理或化学学科中的一些具有反比例函数关系的公式.同时体会数学中的转化思想.
(3)反比例函数中的图表信息题
正确的认识图象,找到关键的点,运用好数形结合的思想.
8.反比例函数综合题
(1)应用类综合题
能够从实际的问题中抽象出反比例函数这一数学模型,是解决实际问题的关键一步,培养了学生的建模能力和从实际问题向数学问题转化的能力.在解决这些问题的时候我们还用到了反比例函数的图象和性质、待定系数法和其他学科中的知识.
(2)数形结合类综合题
利用图象解决问题,从图上获取有用的信息,是解题的关键所在.已知点在图象上,那么点一定满足这个函数解析式,反过来如果这点满足函数的解析式,那么这个点也一定在函数图象上.还能利用图象直接比较函数值或是自变量的大小.将数形结合在一起,是分析解决问题的一种好方法.
【真题汇编】2023年中考数学备考之反比例函数
(选择题60题)
满分:120分 建议时间:100分钟
学校:___________姓名:___________班级:___________考号:___________
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息2.请将答案正确填写在答题卡上
一.选择题(共60小题,满分120分,每小题2分)
1.(2分)(2022 襄阳)二次函数y=ax2+bx+c的图象如图所示,则一次函数y=bx+c和反比例函数y=在同一平面直角坐标系中的图象可能是( )
A. B.
C. D.
2.(2分)(2022 西藏)在同一平面直角坐标系中,函数y=ax+b与y=(其中a,b是常数,ab≠0)的大致图象是( )
A. B.
C. D.
3.(2分)(2022 张家界)在同一平面直角坐标系中,函数y=kx+1(k≠0)和y=(k≠0)的图象大致是( )
A. B.
C. D.
4.(2分)(2022 绥化)已知二次函数y=ax2+bx+c的部分函数图象如图所示,则一次函数y=ax+b2﹣4ac与反比例函数y=在同一平面直角坐标系中的图象大致是( )
A. B.
C. D.
5.(2分)(2022 贺州)已知一次函数y=kx+b的图象如图所示,则y=﹣kx+b与y=的图象为( )
A. B.
C. D.
6.(2分)(2022 滨州)在同一平面直角坐标系中,函数y=kx+1与y=﹣(k为常数且k≠0)的图象大致是( )
A. B.
C. D.
7.(2分)(2021 遵义)已知反比例函数y=(k≠0)的图象如图所示,则一次函数y=kx+2的图象经过( )
A.第一、二、三象限 B.第一、三、四象限
C.第一、二、四象限 D.第二、三、四象限
8.(2分)(2022 黔西南州)在平面直角坐标系中,反比例函数y=(k≠0)的图象如图所示,则一次函数y=kx+2的图象经过的象限是( )
A.一、二、三 B.一、二、四 C.一、三、四 D.二、三、四
9.(2分)(2022 上海)已知反比例函数y=(k≠0),且在各自象限内,y随x的增大而增大,则下列点可能在这个函数图象上的为( )
A.(2,3) B.(﹣2,3) C.(3,0) D.(﹣3,0)
10.(2分)(2022 广东)点(1,y1),(2,y2),(3,y3),(4,y4)在反比例函数y=图象上,则y1,y2,y3,y4中最小的是( )
A.y1 B.y2 C.y3 D.y4
11.(2分)(2021 黔西南州)对于反比例函数y=,下列说法错误的是( )
A.图象经过点(1,﹣5)
B.图象位于第二、第四象限
C.当x<0时,y随x的增大而减小
D.当x>0时,y随x的增大而增大
12.(2分)(2022 荆门)如图,点A,C为函数y=(x<0)图象上的两点,过A,C分别作AB⊥x轴,CD⊥x轴,垂足分别为B,D,连接OA,AC,OC,线段OC交AB于点E,且点E恰好为OC的中点.当△AEC的面积为时,k的值为( )
A.﹣1 B.﹣2 C.﹣3 D.﹣4
13.(2分)(2021 德州)小红同学在研究函数y=|x|+的图象时,发现有如下结论:①该函数有最小值;②该函数图象与坐标轴无交点;③当x>0时,y随x的增大而增大;④该函数图象关于y轴对称;⑤直线y=8与该函数图象有两个交点,则上述结论中正确的个数为( )
A.2个 B.3个 C.4个 D.5个
14.(2分)(2021 济南)反比例函数y=(k≠0)图象的两个分支分别位于第一、三象限,则一次函数y=kx﹣k的图象大致是( )
A. B. C. D.
15.(2分)(2021 阜新)已知点A(x1,y1),B(x2,y2)都在反比例函数y=﹣的图象上,且x1<0<x2,则y1,y2的关系一定成立的是( )
A.y1>y2 B.y1<y2 C.y1+y2=0 D.y1﹣y2=0
16.(2分)(2021 湘西州)如图所示,小英同学根据学习函数的经验,自主尝试在平面直角坐标系中画出了一个解析式为y=的函数图象.根据这个函数的图象,下列说法正确的是( )
A.图象与x轴没有交点
B.当x>0时,y>0
C.图象与y轴的交点是(0,﹣)
D.y随x的增大而减小
17.(2分)(2021 兰州)如图,点A在反比例函数y=(x>0)图象上,AB⊥x轴于点B,C是OB的中点,连接AO,AC,若△AOC的面积为2,则k=( )
A.4 B.8 C.12 D.16
18.(2分)(2022 日照)如图,矩形OABC与反比例函数y1=(k1是非零常数,x>0)的图象交于点M,N,与反比例函数y2=(k2是非零常数,x>0)的图象交于点B,连接OM,ON.若四边形OMBN的面积为3,则k1﹣k2=( )
A.3 B.﹣3 C. D.
19.(2分)(2022 牡丹江)如图,等边三角形OAB,点B在x轴正半轴上,S△OAB=4,若反比例函数y=(k≠0)图象的一支经过点A,则k的值是( )
A. B. C. D.
20.(2分)(2022 通辽)如图,点D是 OABC内一点,AD与x轴平行,BD与y轴平行,BD=,∠BDC=120°,S△BCD=,若反比例函数y=(x<0)的图象经过C,D两点,则k的值是( )
A.﹣6 B.﹣6 C.﹣12 D.﹣12
21.(2分)(2022 郴州)如图,在函数y=(x>0)的图象上任取一点A,过点A作y轴的垂线交函数y=﹣(x<0)的图象于点B,连接OA,OB,则△AOB的面积是( )
A.3 B.5 C.6 D.10
22.(2分)(2021 牡丹江)如图,矩形OABC的面积为36,它的对角线OB与双曲线y=相交于点D,且OD:OB=2:3,则k的值为( )
A.12 B.﹣12 C.16 D.﹣16
23.(2分)(2022 黑龙江)如图,在平面直角坐标系中,点O为坐标原点,平行四边形OBAD的顶点B在反比例函数y=的图象上,顶点A在反比例函数y=的图象上,顶点D在x轴的负半轴上.若平行四边形OBAD的面积是5,则k的值是( )
A.2 B.1 C.﹣1 D.﹣2
24.(2分)(2022 十堰)如图,正方形ABCD的顶点分别在反比例函数y=(k1>0)和y=(k2>0)的图象上.若BD∥y轴,点D的横坐标为3,则k1+k2=( )
A.36 B.18 C.12 D.9
25.(2分)(2021 兰州)如图,点A在反比例函数y=(x>0)的图象上,AB⊥x轴于点B,C是OB的中点,连接AO,AC,若△AOC的面积为4,则k=( )
A.16 B.12 C.8 D.4
26.(2分)(2021 西藏)如图.在平面直角坐标系中,△AOB的面积为,BA垂直x轴于点A,OB与双曲线y=相交于点C,且BC:OC=1:2.则k的值为( )
A.﹣3 B.﹣ C.3 D.
27.(2分)(2021 丹东)如图,点A在双曲线y1=(x>0)上,点B在双曲线y2=(x<0)上,AB∥x轴,点C是x轴上一点,连接AC、BC,若△ABC的面积是6,则k的值( )
A.﹣6 B.﹣8 C.﹣10 D.﹣12
28.(2分)(2021 黑龙江)如图,在平面直角坐标系中,矩形ABCD的顶点A在双曲线y=﹣(x<0)上,点C,D在y轴的正半轴上,点E在BC上,CE=2BE,连接DE并延长,交x轴于点F,连接CF,则△FCD的面积为( )
A.2 B. C.1 D.
29.(2分)(2021 淄博)如图,在平面直角坐标系中,四边形AOBD的边OB与x轴的正半轴重合,AD∥OB,DB⊥x轴,对角线AB,OD交于点M.已知AD:OB=2:3,△AMD的面积为4.若反比例函数y=的图象恰好经过点M,则k的值为( )
A. B. C. D.12
30.(2分)(2021 兴安盟)点(﹣5,y1),(﹣3,y2),(3,y3)都在反比例函数y=(k>0)的图象上,则( )
A.y1>y2>y3 B.y3>y1>y2 C.y2>y1>y3 D.y1>y3>y2
31.(2分)(2021 德州)已知点A(x1,y1),B(x2,y2),C(x3,y3)都在反比例函数y=(a是常数)的图象上,且y1<y2<0<y3,则x1,x2,x3的大小关系为( )
A.x2>x1>x3 B.x1>x2>x3 C.x3>x2>x1 D.x3>x1>x2
32.(2分)(2022 阜新)已知反比例函数y=(k≠0)的图象经过点(﹣2,4),那么该反比例函数图象也一定经过点( )
A.(4,2) B.(1,8) C.(﹣1,8) D.(﹣1,﹣8)
33.(2分)(2022 襄阳)若点A(﹣2,y1),B(﹣1,y2)都在反比例函数y=的图象上,则y1,y2的大小关系是( )
A.y1<y2 B.y1=y2 C.y1>y2 D.不能确定
34.(2分)(2022 枣庄)如图,正方形ABCD的边长为5,点A的坐标为(4,0),点B在y轴上,若反比例函数y=(k≠0)的图象过点C,则k的值为( )
A.4 B.﹣4 C.﹣3 D.3
35.(2分)(2022 长春)如图,在平面直角坐标系中,点P在反比例函数y=(k>0,x>0)的图象上,其纵坐标为2,过点P作PQ∥y轴,交x轴于点Q,将线段QP绕点Q顺时针旋转60°得到线段QM.若点M也在该反比例函数的图象上,则k的值为( )
A. B. C. D.4
36.(2分)(2022 贵阳)如图,在平面直角坐标系中有P,Q,M,N四个点,其中恰有三点在反比例函数y=(k>0)的图象上.根据图中四点的位置,判断这四个点中不在函数y=的图象上的点是( )
A.点P B.点Q C.点M D.点N
37.(2分)(2022 娄底)在平面直角坐标系中,O为坐标原点,已知点P(m,1)、Q(1,m)(m>0且m≠1),过点P、Q的直线与两坐标轴相交于A、B两点,连接OP、OQ,则下列结论中成立的有( )
①点P、Q在反比例函数y=的图象上;
②△AOB为等腰直角三角形;
③0°<∠POQ<90°;
④∠POQ的值随m的增大而增大.
A.②③④ B.①③④ C.①②④ D.①②③
38.(2分)(2022 天津)若点A(x1,2),B(x2,﹣1),C(x3,4)都在反比例函数y=的图象上,则x1,x2,x3的大小关系是( )
A.x1<x2<x3 B.x2<x3<x1 C.x1<x3<x2 D.x2<x1<x3
39.(2分)(2021 内江)如图,菱形ABCD的顶点分别在反比例函数y=和y=的图象上,若∠BCD=60°,则的值为( )
A. B. C. D.
40.(2分)(2021 朝阳)如图,O是坐标原点,点B在x轴上,在△OAB中,AO=AB=5,OB=6,点A在反比例函数y=(k≠0)图象上,则k的值( )
A.﹣12 B.﹣15 C.﹣20 D.﹣30
41.(2分)(2021 大连)下列说法正确的是( )
①反比例函数y=中自变量x的取值范围是x≠0;
②点P(﹣3,2)在反比例函数y=﹣的图象上;
③反比例函数y=的图象,在每一个象限内,y随x的增大而增大.
A.①② B.①③ C.②③ D.①②③
42.(2分)(2022 海南)若反比例函数y=(k≠0)的图象经过点(2,﹣3),则它的图象也一定经过的点是( )
A.(﹣2,﹣3) B.(﹣3,﹣2) C.(1,﹣6) D.(6,1)
43.(2分)(2022 武汉)已知点A(x1,y1),B(x2,y2)在反比例函数y=的图象上,且x1<0<x2,则下列结论一定正确的是( )
A.y1+y2<0 B.y1+y2>0 C.y1<y2 D.y1>y2
44.(2分)(2022 宿迁)如图,点A在反比例函数y=(x>0)的图象上,以OA为一边作等腰直角三角形OAB,其中∠OAB=90°,AO=AB,则线段OB长的最小值是( )
A.1 B. C.2 D.4
45.(2分)(2021 益阳)正比例函数y=2x与反比例函数y=的图象或性质的共有特征之一是( )
A.函数值y随x的增大而增大
B.图象在第一、三象限都有分布
C.图象与坐标轴有交点
D.图象经过点(2,1)
46.(2分)(2021 滨州)如图,在△OAB中,∠BOA=45°,点C为边AB上一点,且BC=2AC.如果函数y=(x>0)的图象经过点B和点C,那么用下列坐标表示的点,在直线BC上的是( )
A.(﹣2019,674) B.(﹣2020,675)
C.(2021,﹣669) D.(2022,﹣670)
47.(2分)(2021 广州)在平面直角坐标系xOy中,矩形OABC的顶点A在函数y=(x>0)的图象上,顶点C在函数y=﹣(x<0)的图象上,若顶点B的横坐标为﹣,则点A的坐标为( )
A.(,2) B.(,) C.(2,) D.(,)
48.(2分)(2022 东营)如图,一次函数y1=k1x+b与反比例函数y2=的图象相交于A,B两点,点A的横坐标为2,点B的横坐标为﹣1,则不等式k1x+b<的解集是( )
A.﹣1<x<0或x>2 B.x<﹣1或0<x<2
C.x<﹣1或x>2 D.﹣1<x<2
49.(2分)(2022 无锡)一次函数y=mx+n的图象与反比例函数y=的图象交于点A、B,其中点A、B的坐标为A(﹣,﹣2m)、B(m,1),则△OAB的面积是( )
A.3 B. C. D.
50.(2分)(2022 攀枝花)如图,正比例函数y=k1x与反比例函数y=的图象交于A(1,m)、B两点,当k1x≤时,x的取值范围是( )
A.﹣1≤x<0或x≥1 B.x≤﹣1或0<x≤1
C.x≤﹣1或x≥1 D.﹣1≤x<0或0<x≤1
51.(2分)(2022 朝阳)如图,正比例函数y=ax(a为常数,且a≠0)和反比例函数y=(k为常数,且k≠0)的图象相交于A(﹣2,m)和B两点,则不等式ax>的解集为( )
A.x<﹣2或x>2 B.﹣2<x<2
C.﹣2<x<0或x>2 D.x<﹣2或0<x<2
52.(2分)(2022 怀化)如图,直线AB交x轴于点C,交反比例函数y=(a>1)的图象于A、B两点,过点B作BD⊥y轴,垂足为点D,若S△BCD=5,则a的值为( )
A.8 B.9 C.10 D.11
53.(2分)(2021 无锡)在平面直角坐标系中,O为坐标原点,点A(a,2)是反比例函数的图象上的点,连接AO并延长与反比例函数图象交于另一点B,将直线AB向下平移,与反比例函数的图象交于C、D两点.若△ABC的面积为5,则向下平移的距离是( )
A.3 B.5 C.4 D.
54.(2分)(2022 荆州)如图是同一直角坐标系中函数y1=2x和y2=的图象.观察图象可得不等式2x>的解集为( )
A.﹣1<x<1 B.x<﹣1或x>1
C.x<﹣1或0<x<1 D.﹣1<x<0或x>1
55.(2分)(2021 梧州)如图,在同一平面直角坐标系中,直线y=t(t为常数)与反比例函数y1=,y2=﹣的图象分别交于点A,B,连接OA,OB,则△OAB的面积为( )
A.5t B. C. D.5
56.(2分)(2022 内江)如图,在平面直角坐标系中,点M为x轴正半轴上一点,过点M的直线l∥y轴,且直线l分别与反比例函数y=和y=的图象交于P、Q两点.若S△POQ=15,则k的值为( )
A.38 B.22 C.﹣7 D.﹣22
57.(2分)(2021 南通)平面直角坐标系xOy中,直线y=2x与双曲线y=(k>2)相交于A,B两点,其中点A在第一象限.设M(m,2)为双曲线y=(k>2)上一点,直线AM,BM分别交y轴于C,D两点,则OC﹣OD的值为( )
A.2 B.4 C.6 D.8
58.(2分)(2022 宜昌)已知经过闭合电路的电流I(单位:A)与电路的电阻R(单位:Ω)是反比例函数关系.根据下表判断a和b的大小关系为( )
I/A 5 … a … … … b … 1
R/Ω 20 30 40 50 60 70 80 90 100
A.a>b B.a≥b C.a<b D.a≤b
59.(2分)(2022 宁夏)在显示汽车油箱内油量的装置模拟示意图中,电压U一定时,油箱中浮子随油面下降而落下,带动滑杆使滑动变阻器滑片向上移动,从而改变电路中的电流,电流表的示数对应油量体积,把电流表刻度改为相应油量体积数,由此知道油箱里剩余油量.在不考虑其他因素的条件下,油箱中油的体积V与电路中总电阻R总(R总=R+R0)是反比例关系,电流I与R总也是反比例关系,则I与V的函数关系是( )
A.反比例函数 B.正比例函数
C.二次函数 D.以上答案都不对
60.(2分)(2022 丽水)已知电灯电路两端的电压U为220V,通过灯泡的电流强度I(A)的最大限度不得超过0.11A.设选用灯泡的电阻为R(Ω),下列说法正确的是( )
A.R至少2000Ω B.R至多2000Ω C.R至少24.2Ω D.R至多24.2Ω
【真题汇编】2023年中考数学备考之反比例函数(选择题60题)
参考答案与试题解析
一.选择题(共60小题,满分120分,每小题2分)
1.(2分)(2022 襄阳)二次函数y=ax2+bx+c的图象如图所示,则一次函数y=bx+c和反比例函数y=在同一平面直角坐标系中的图象可能是( )
A. B.
C. D.
【解析】解:∵二次函数图象开口方向向下,
∴a<0,
∵对称轴为直线x=﹣>0,
∴b>0,
∵与y轴的负半轴相交,
∴c<0,
∴y=bx+c的图象经过第一、三、四象限,
反比例函数y=图象在第二四象限,
只有D选项图象符合.
故选:D.
2.(2分)(2022 西藏)在同一平面直角坐标系中,函数y=ax+b与y=(其中a,b是常数,ab≠0)的大致图象是( )
A. B.
C. D.
【解析】解:若a>0,b>0,
则y=ax+b经过一、二、三象限,反比例函数y=(ab≠0)位于一、三象限,
若a>0,b<0,
则y=ax+b经过一、三、四象限,反比例函数数y=(ab≠0)位于二、四象限,
若a<0,b>0,
则y=ax+b经过一、二、四象限,反比例函数y=(ab≠0)位于二、四象限,
若a<0,b<0,
则y=ax+b经过二、三、四象限,反比例函数y=(ab≠0)位于一、三象限,
故选:A.
3.(2分)(2022 张家界)在同一平面直角坐标系中,函数y=kx+1(k≠0)和y=(k≠0)的图象大致是( )
A. B.
C. D.
【解析】解:当k>0时,一次函数y=kx+1经过第一、二、三象限,反比例函数y=位于第一、三象限;
当k<0时,一次函数y=kx+1经过第一、二、四象限,反比例函数y=位于第二、四象限;
故选:D.
4.(2分)(2022 绥化)已知二次函数y=ax2+bx+c的部分函数图象如图所示,则一次函数y=ax+b2﹣4ac与反比例函数y=在同一平面直角坐标系中的图象大致是( )
A. B.
C. D.
【解析】解:∵二次函数y=ax2+bx+c的部分函数图象开口向上,
∴a>0,
∵二次函数y=ax2+bx+c的部分函数图象顶点在x轴下方,开口向上,
∴二次函数y=ax2+bx+c的图象与x轴有两个交点,b2﹣4ac>0,
∴一次函数y=ax+b2﹣4ac的图象位于第一,二,三象限,
由二次函数y=ax2+bx+c的部分函数图象可知,点(2,4a+2b+c)在x轴上方,
∴4a+2b+c>0,
∴y=的图象位于第一,三象限,
据此可知,符合题意的是B,
故选:B.
5.(2分)(2022 贺州)已知一次函数y=kx+b的图象如图所示,则y=﹣kx+b与y=的图象为( )
A. B.
C. D.
【解析】解:根据一次函数y=kx+b的图象位置,可判断k>0、b>0.
所以﹣k<0.
再根据一次函数和反比例函数的图像和性质,
故选:A.
6.(2分)(2022 滨州)在同一平面直角坐标系中,函数y=kx+1与y=﹣(k为常数且k≠0)的图象大致是( )
A. B.
C. D.
【解析】解:当k>0时,则﹣k<0,一次函数y=kx+1图象经过第一、二、三象限,反比例函数图象在第二、四象限,所以A选项正确,C选项错误;
当k<0时,一次函数y=kx+1图象经过第一、二,四象限,所以B、D选项错误.
故选:A.
7.(2分)(2021 遵义)已知反比例函数y=(k≠0)的图象如图所示,则一次函数y=kx+2的图象经过( )
A.第一、二、三象限 B.第一、三、四象限
C.第一、二、四象限 D.第二、三、四象限
【解析】解:由反比例函数图象经过二、四象限,可知,k<0,
∴y=kx+2的图象经过一、二、四象限.
故选:C.
8.(2分)(2022 黔西南州)在平面直角坐标系中,反比例函数y=(k≠0)的图象如图所示,则一次函数y=kx+2的图象经过的象限是( )
A.一、二、三 B.一、二、四 C.一、三、四 D.二、三、四
【解析】解:由图可知:k<0,
∴一次函数y=kx+2的图象经过的象限是一、二、四.
故选:B.
9.(2分)(2022 上海)已知反比例函数y=(k≠0),且在各自象限内,y随x的增大而增大,则下列点可能在这个函数图象上的为( )
A.(2,3) B.(﹣2,3) C.(3,0) D.(﹣3,0)
【解析】解:因为反比例函数y=(k≠0),且在各自象限内,y随x的增大而增大,
所以k<0,
A.2×3=6>0,故本选项不符合题意;
B.﹣2×3=﹣6<0,故本选项符合题意;
C.3×0=0,故本选项不符合题意;
D.﹣3×0=0,故本选项不符合题意;
故选:B.
10.(2分)(2022 广东)点(1,y1),(2,y2),(3,y3),(4,y4)在反比例函数y=图象上,则y1,y2,y3,y4中最小的是( )
A.y1 B.y2 C.y3 D.y4
【解析】解:∵k=4>0,
∴在第一象限内,y随x的增大而减小,
∵(1,y1),(2,y2),(3,y3),(4,y4)在反比例函数y=图象上,且1<2<3<4,
∴y4最小.
故选:D.
11.(2分)(2021 黔西南州)对于反比例函数y=,下列说法错误的是( )
A.图象经过点(1,﹣5)
B.图象位于第二、第四象限
C.当x<0时,y随x的增大而减小
D.当x>0时,y随x的增大而增大
【解析】解:∵反比例函数y=,
∴当x=1时,y=﹣=﹣5,故选项A不符合题意;
k=﹣5,故该函数图象位于第二、四象限,故选项B不符合题意;
当x<0,y随x的增大而增大,故选项C符合题意;
当x>0时,y随x的增大而增大,故选项D不符合题意;
故选:C.
12.(2分)(2022 荆门)如图,点A,C为函数y=(x<0)图象上的两点,过A,C分别作AB⊥x轴,CD⊥x轴,垂足分别为B,D,连接OA,AC,OC,线段OC交AB于点E,且点E恰好为OC的中点.当△AEC的面积为时,k的值为( )
A.﹣1 B.﹣2 C.﹣3 D.﹣4
【解析】解:∵点E为OC的中点,
∴△AEO的面积=△AEC的面积=,
∵点A,C为函数y=(x<0)图象上的两点,
∴S△ABO=S△CDO,
∴S四边形CDBE=S△AEO=,
∵EB∥CD,
∴△OEB∽△OCD,
∴=()2,
∴S△OCD=1,
则xy=﹣1,
∴k=xy=﹣2.
故选:B.
13.(2分)(2021 德州)小红同学在研究函数y=|x|+的图象时,发现有如下结论:①该函数有最小值;②该函数图象与坐标轴无交点;③当x>0时,y随x的增大而增大;④该函数图象关于y轴对称;⑤直线y=8与该函数图象有两个交点,则上述结论中正确的个数为( )
A.2个 B.3个 C.4个 D.5个
【解析】解:列表:
x … ﹣4 ﹣3 ﹣2 ﹣1 1 2 3 4 …
y … 5 4 5 5 4 5 …
画出函数图象如图,
观察图象:
①该函数有最小值,符合题意;
②该函数图象与坐标轴无交点,符合题意;
③当x>0时,y随x的增大而增大,不合题意;
④该函数图象关于y轴对称,符合题意;
⑤令|x|+=8,整理得x2﹣8x+4=0或x2+8x+4=0,
∵Δ=82﹣4×1×4>0,
∴两个方程均有两个不相等的实数根,即共有四个根,且这四个根互不相等.
∴直线y=8与该函数图象有四个交点,不符合题意,
综上,以上结论正确的有:①②④,
故选:B.
14.(2分)(2021 济南)反比例函数y=(k≠0)图象的两个分支分别位于第一、三象限,则一次函数y=kx﹣k的图象大致是( )
A. B. C. D.
【解析】解:∵反比例函数y=(k≠0)图象的两个分支分别位于第一、三象限,
∴k>0,
∴﹣k<0,
∴一次函数y=kx﹣k的图象图象经过第一、三、四象限,
故选:D.
15.(2分)(2021 阜新)已知点A(x1,y1),B(x2,y2)都在反比例函数y=﹣的图象上,且x1<0<x2,则y1,y2的关系一定成立的是( )
A.y1>y2 B.y1<y2 C.y1+y2=0 D.y1﹣y2=0
【解析】解:∵反比例函数y=﹣中k=﹣1<0,
∴函数图象的两个分支分别位于二、四象限,且在每一象限内,y随x的增大而增大.
∵x1<0<x2,
∴A在第二象限,B在第四象限,
∴y1>0,y2<0,
∴y1>y2.
故选:A.
16.(2分)(2021 湘西州)如图所示,小英同学根据学习函数的经验,自主尝试在平面直角坐标系中画出了一个解析式为y=的函数图象.根据这个函数的图象,下列说法正确的是( )
A.图象与x轴没有交点
B.当x>0时,y>0
C.图象与y轴的交点是(0,﹣)
D.y随x的增大而减小
【解析】解:A.由图象可知,图象与x轴没有交点,故说法正确;
B.由图象可知,当0<x<1时,y<0,当x>1时,y>0,故说法错误;
C.当x=0时,函数值为﹣2,故图象与y轴的交点是(0,﹣2),故说法错误;
D.当x>1时,y随x的增大而减小,当x<1时,y随x的增大而减小,故说法错误.
故选:A.
17.(2分)(2021 兰州)如图,点A在反比例函数y=(x>0)图象上,AB⊥x轴于点B,C是OB的中点,连接AO,AC,若△AOC的面积为2,则k=( )
A.4 B.8 C.12 D.16
【解析】解:∵C是OB的中点,△AOC的面积为2,
∴△AOB的面积为4,
∵AB⊥x轴,
∴AB OB=4,
∴AB OB=8,
∴k=8.
故选:B.
18.(2分)(2022 日照)如图,矩形OABC与反比例函数y1=(k1是非零常数,x>0)的图象交于点M,N,与反比例函数y2=(k2是非零常数,x>0)的图象交于点B,连接OM,ON.若四边形OMBN的面积为3,则k1﹣k2=( )
A.3 B.﹣3 C. D.
【解析】解:∵y1、y2的图象均在第一象限,
∴k1>0,k2>0,
∵点M、N均在反比例函数y1=(k1是非零常数,x>0)的图象上,
∴S△OAM=S△OCN=k1,
∵矩形OABC的顶点B在反比例函数y2=(k2是非零常数,x>0)的图象上,
∴S矩形OABC=k2,
∴S四边形OMBN=S矩形OABC﹣S△OAM﹣S△OCN=3,
∴k2﹣k1=3,
∴k1﹣k2=﹣3,
故选:B.
19.(2分)(2022 牡丹江)如图,等边三角形OAB,点B在x轴正半轴上,S△OAB=4,若反比例函数y=(k≠0)图象的一支经过点A,则k的值是( )
A. B. C. D.
【解析】解:如图,过点A作AC⊥OB于点C,
∵△OAB是正三角形,
∴OC=BC,
∴S△AOC=S△AOB=2=|k|,
又∵k>0,
∴k=4,
故选:D.
20.(2分)(2022 通辽)如图,点D是 OABC内一点,AD与x轴平行,BD与y轴平行,BD=,∠BDC=120°,S△BCD=,若反比例函数y=(x<0)的图象经过C,D两点,则k的值是( )
A.﹣6 B.﹣6 C.﹣12 D.﹣12
【解析】解:过点C作CE⊥y轴,延长BD交CE于点F,
∵四边形OABC为平行四边形,
∴AB∥OC,AB=OC,
∴∠COE=∠1,
∵BD与y轴平行,
∴∠1=∠ABD,∠ADB=90°,
∴∠COE=∠ABD,
在△COE和△ABD中,
,
∴△COE≌△ABD(AAS),
∴OE=BD=,
∵S△BDC=BD CF=,
∴CF=9,
∵∠BDC=120°,
∴∠CDF=60°,
∴DF=3,
点D的纵坐标为4,
设C(m,),则D(m+9,4),
∵反比例函数y=(x<0)的图象经过C,D两点,
∴k=m=4(m+9),
∴m=﹣12,
∴k=﹣12,
故选:C.
21.(2分)(2022 郴州)如图,在函数y=(x>0)的图象上任取一点A,过点A作y轴的垂线交函数y=﹣(x<0)的图象于点B,连接OA,OB,则△AOB的面积是( )
A.3 B.5 C.6 D.10
【解析】解:∵点A在函数y=(x>0)的图象上,
∴S△AOC=×2=1,
又∵点B在反比例函数y=﹣(x<0)的图象上,
∴S△BOC=×8=4,
∴S△AOB=S△AOC+S△BOC
=1+4
=5,
故选:B.
22.(2分)(2021 牡丹江)如图,矩形OABC的面积为36,它的对角线OB与双曲线y=相交于点D,且OD:OB=2:3,则k的值为( )
A.12 B.﹣12 C.16 D.﹣16
【解析】解:方法一、如图,连接CD,过点D作DE⊥CO于E,
∵矩形OABC的面积为36,
∴S△BCO=18,
∵OD:OB=2:3,
∴S△CDO==12,
∵DE⊥CO,BC⊥CO,
∴DE∥BC,
∴,
∴S△DEO==8,
∵双曲线y=图象过点D,
∴=8,
又∵双曲线y=图象在第二象限,
∴k<0,
∴k=﹣16,
方法二、∵矩形OABC的面积为36,
∴S△BCO=18,
∵DE∥BC,
∴=()2=,
∴S△DEO=18×=8,
∵双曲线y=图象过点D,
∴=8,
又∵双曲线y=图象在第二象限,
∴k<0,
∴k=﹣16,
故选:D.
23.(2分)(2022 黑龙江)如图,在平面直角坐标系中,点O为坐标原点,平行四边形OBAD的顶点B在反比例函数y=的图象上,顶点A在反比例函数y=的图象上,顶点D在x轴的负半轴上.若平行四边形OBAD的面积是5,则k的值是( )
A.2 B.1 C.﹣1 D.﹣2
【解析】解:设B(a,),
∵四边形OBAD是平行四边形,
∴AB∥DO,
∴A(,),
∴AB=a﹣,
∵平行四边形OBAD的面积是5,
∴(a﹣)=5,
解得k=﹣2,
故选:D.
24.(2分)(2022 十堰)如图,正方形ABCD的顶点分别在反比例函数y=(k1>0)和y=(k2>0)的图象上.若BD∥y轴,点D的横坐标为3,则k1+k2=( )
A.36 B.18 C.12 D.9
【解析】解:连接AC交BD于E,延长BD交x轴于F,连接OD、OB,如图:
∵四边形ABCD是正方形,
∴AE=BE=CE=DE,
设AE=BE=CE=DE=m,D(3,a),
∵BD∥y轴,
∴B(3,a+2m),A(3+m,a+m),
∵A,B都在反比例函数y=(k1>0)的图象上,
∴k1=3(a+2m)=(3+m)(a+m),
∵m≠0,
∴m=3﹣a,
∴B(3,6﹣a),
∵B(3,6﹣a)在反比例函数y=(k1>0)的图象上,D(3,a)在y=(k2>0)的图象上,
∴k1=3(6﹣a)=18﹣3a,k2=3a,
∴k1+k2=18﹣3a+3a=18;
故选:B.
25.(2分)(2021 兰州)如图,点A在反比例函数y=(x>0)的图象上,AB⊥x轴于点B,C是OB的中点,连接AO,AC,若△AOC的面积为4,则k=( )
A.16 B.12 C.8 D.4
【解析】解:∵C是OB的中点,△AOC的面积为4,
∴△AOB的面积为8,
设A(a,b)
∵AB⊥x轴于点B,
∴ab=16,
∵点A在反比例函数y=(x>0)的图象上,
∴k=16.
故选:A.
26.(2分)(2021 西藏)如图.在平面直角坐标系中,△AOB的面积为,BA垂直x轴于点A,OB与双曲线y=相交于点C,且BC:OC=1:2.则k的值为( )
A.﹣3 B.﹣ C.3 D.
【解析】解:过C作CD⊥x轴于D,
∵=,
∴=,
∵BA⊥x轴,
∴CD∥AB,
∴△DOC∽△AOB,
∴=()2=()2=,
∵S△AOB=,
∴S△DOC=S△AOB=×=,
∵双曲线y=在第二象限,
∴k=﹣2×=﹣3,
故选:A.
27.(2分)(2021 丹东)如图,点A在双曲线y1=(x>0)上,点B在双曲线y2=(x<0)上,AB∥x轴,点C是x轴上一点,连接AC、BC,若△ABC的面积是6,则k的值( )
A.﹣6 B.﹣8 C.﹣10 D.﹣12
【解析】解:如图,连接OA,OB,AB与y轴交于点M,
∵AB∥x轴,点A双在曲线y1=(x>0)上,点B在双曲线y2=(x<0)上,
∴S△AOM=×|2|=1,S△BOM=×|k|=﹣k,
∵S△ABC=S△AOB=6,
∴1﹣k=6,
∴k=﹣10.
故选:C.
28.(2分)(2021 黑龙江)如图,在平面直角坐标系中,矩形ABCD的顶点A在双曲线y=﹣(x<0)上,点C,D在y轴的正半轴上,点E在BC上,CE=2BE,连接DE并延长,交x轴于点F,连接CF,则△FCD的面积为( )
A.2 B. C.1 D.
【解析】解:根据题意,设A(n,﹣),D(0,﹣),
设OC=m,则C(0,m),CD=﹣﹣m,
∴B(n,m),BC=﹣n,
∵CE=2BE,
∴CE=BC=﹣n,
∴E(n,m),
由题知BC∥FO,
∴∠DEC=∠DFO,∠DCE=∠DOF,
∴△DEC∽△DFO,
∴=,
即=,
∴FO=,
∴S△FCD=FO CD=×(﹣﹣m)=1,
故选:C.
29.(2分)(2021 淄博)如图,在平面直角坐标系中,四边形AOBD的边OB与x轴的正半轴重合,AD∥OB,DB⊥x轴,对角线AB,OD交于点M.已知AD:OB=2:3,△AMD的面积为4.若反比例函数y=的图象恰好经过点M,则k的值为( )
A. B. C. D.12
【解析】解:过点M作MH⊥OB于H.
∵AD∥OB,
∴△ADM∽△BOM,
∴=()2=,
∵S△ADM=4,
∴S△BOM=9,
∵DB⊥OB,MH⊥OB,
∴MH∥DB,
∴===,
∴OH=OB,
∴S△MOH=×S△OBM=,
∵=,
∴k=,
故选:B.
30.(2分)(2021 兴安盟)点(﹣5,y1),(﹣3,y2),(3,y3)都在反比例函数y=(k>0)的图象上,则( )
A.y1>y2>y3 B.y3>y1>y2 C.y2>y1>y3 D.y1>y3>y2
【解析】解:∵反比例函数y=中k>0,
∴函数图象的两个分支分别位于一、三象限,且在每一象限内y随x的增大而减小.
∵﹣5<﹣3<0,
∴0>y1>y2,
∵3>0,
∴y3>0,
∴y3>y1>y2,
故选:B.
31.(2分)(2021 德州)已知点A(x1,y1),B(x2,y2),C(x3,y3)都在反比例函数y=(a是常数)的图象上,且y1<y2<0<y3,则x1,x2,x3的大小关系为( )
A.x2>x1>x3 B.x1>x2>x3 C.x3>x2>x1 D.x3>x1>x2
【解析】解:∵a2+1>0,
∴反比例函数y=(a是常数)的图象在一、三象限,
如图所示,当y1<y2<0<y3时,x3>0>x1>x2,
故选:D.
32.(2分)(2022 阜新)已知反比例函数y=(k≠0)的图象经过点(﹣2,4),那么该反比例函数图象也一定经过点( )
A.(4,2) B.(1,8) C.(﹣1,8) D.(﹣1,﹣8)
【解析】解:∵反比例函数y=(k≠0)的图象经过点(﹣2,4),
∴k=﹣2×4=﹣8,
A、∵4×2=8≠﹣8,∴此点不在反比例函数的图象上,故本选项错误;
B、∵1×8=8≠﹣8,∴此点不在反比例函数的图象上,故本选项错误;
C、﹣1×8=﹣8,∴此点在反比例函数的图象上,故本选项正确;
D、(﹣1)×(﹣8)=8≠﹣8,∴此点不在反比例函数的图象上,故本选项错误.
故选:C.
33.(2分)(2022 襄阳)若点A(﹣2,y1),B(﹣1,y2)都在反比例函数y=的图象上,则y1,y2的大小关系是( )
A.y1<y2 B.y1=y2 C.y1>y2 D.不能确定
【解析】解:∵点A(﹣2,y1),B(﹣1,y2)都在反比例函数y=的图象上,k=2>0,
∴在每个象限内y随x的增大而减小,
∵﹣2<﹣1,
∴y1>y2,
故选:C.
34.(2分)(2022 枣庄)如图,正方形ABCD的边长为5,点A的坐标为(4,0),点B在y轴上,若反比例函数y=(k≠0)的图象过点C,则k的值为( )
A.4 B.﹣4 C.﹣3 D.3
【解析】解:如图,过点C作CE⊥y轴于E,在正方形ABCD中,AB=BC,∠ABC=90°,
∴∠ABO+∠CBE=90°,
∵∠OAB+∠ABO=90°,
∴∠OAB=∠CBE,
∵点A的坐标为(4,0),
∴OA=4,
∵AB=5,
∴OB==3,
在△ABO和△BCE中,
,
∴△ABO≌△BCE(AAS),
∴OA=BE=4,CE=OB=3,
∴OE=BE﹣OB=4﹣3=1,
∴点C的坐标为(﹣3,1),
∵反比例函数y=(k≠0)的图象过点C,
∴k=xy=﹣3×1=﹣3,
故选:C.
35.(2分)(2022 长春)如图,在平面直角坐标系中,点P在反比例函数y=(k>0,x>0)的图象上,其纵坐标为2,过点P作PQ∥y轴,交x轴于点Q,将线段QP绕点Q顺时针旋转60°得到线段QM.若点M也在该反比例函数的图象上,则k的值为( )
A. B. C. D.4
【解析】解:作MN⊥x轴于N,
∵P在反比例函数y=(k>0,x>0)的图象上,其纵坐标为2,过点P作PQ∥y轴,交x轴于点Q,
∴P(,2),
∴PQ=2,
∵将线段QP绕点Q顺时针旋转60°得到线段QM.
∴QM=QP=2,∠PQM=60°,
∴∠MQN=90°﹣60°=30°,
∴MN=QM=1,
∴QN==,
∴M(+,1),
∵点M也在该反比例函数的图象上,
∴k=+,
解得k=2,
故选:C.
36.(2分)(2022 贵阳)如图,在平面直角坐标系中有P,Q,M,N四个点,其中恰有三点在反比例函数y=(k>0)的图象上.根据图中四点的位置,判断这四个点中不在函数y=的图象上的点是( )
A.点P B.点Q C.点M D.点N
通过观察发现,点P、Q、N可能在图象上,点M不在图象上,
故选:C.
37.(2分)(2022 娄底)在平面直角坐标系中,O为坐标原点,已知点P(m,1)、Q(1,m)(m>0且m≠1),过点P、Q的直线与两坐标轴相交于A、B两点,连接OP、OQ,则下列结论中成立的有( )
①点P、Q在反比例函数y=的图象上;
②△AOB为等腰直角三角形;
③0°<∠POQ<90°;
④∠POQ的值随m的增大而增大.
A.②③④ B.①③④ C.①②④ D.①②③
【解析】解:∵点P(m,1)、Q(1,m)(m>0且m≠1),则m 1=1 m=m,
∴点P、Q在反比例函数y=的图象上,故①正确;
设直线PQ为y=kx+b,则,解得,
∴直线PQ为y=﹣x+m+1,
当y=0时,x=m+1;当x=0时,y=m+1,
∴A(m+1,0),B(0,m+1),
∴OA=OB,
∵∠AOB=90°,
∴△AOB为等腰直角三角形,故②正确;
∵点P(m,1)、Q(1,m)(m>0且m≠1),
∴P、Q都在第一象限,
∴0°<∠POQ<90°,故③正确;
∵直线OP为y=x,直线OQ为y=mx,
∴当0<m<1时,∠POQ的值随m的增大而减小,当m>1时,∠POQ的值随m的增大而增大,
故④错误;
故选:D.
38.(2分)(2022 天津)若点A(x1,2),B(x2,﹣1),C(x3,4)都在反比例函数y=的图象上,则x1,x2,x3的大小关系是( )
A.x1<x2<x3 B.x2<x3<x1 C.x1<x3<x2 D.x2<x1<x3
【解析】解:点A(x1,2),B(x2,﹣1),C(x3,4)都在反比例函数y=的图象上,
∴x1==4,x2==﹣8,x3==2.
∴x2<x3<x1,
故选:B.
39.(2分)(2021 内江)如图,菱形ABCD的顶点分别在反比例函数y=和y=的图象上,若∠BCD=60°,则的值为( )
A. B. C. D.
【解析】解:连接AC、BD,
∵四边形ABCD是菱形,
∴AC⊥BD,
∵菱形ABCD的顶点分别在反比例函数y=和y=的图象上,
∴A与C、B与D关于原点对称,
∴AC、BD经过点O,
∴∠BOC=90°,
∵∠BCO=∠BCD=30°,
∴tan30°==,
作BM⊥x轴于M,CN⊥x轴于N,
∵∠BOM+∠NOC=90°=∠NOC+∠NCO,
∴∠BOM=∠NCO,
∵∠OMB=∠CNO=90°,
∴△OMB∽△CNO,
∴=()2,
∴=,
∴=﹣,
故选:D.
40.(2分)(2021 朝阳)如图,O是坐标原点,点B在x轴上,在△OAB中,AO=AB=5,OB=6,点A在反比例函数y=(k≠0)图象上,则k的值( )
A.﹣12 B.﹣15 C.﹣20 D.﹣30
【解析】解:过A点作AC⊥OB,
∵AO=AB,AC⊥OB,OB=6,
∴OC=BC=3,
在Rt△AOC中,OA=5,
∵AC=,
∴A(﹣3,4),
把A(﹣3,4)代入y=,可得k=﹣12,
故选:A.
41.(2分)(2021 大连)下列说法正确的是( )
①反比例函数y=中自变量x的取值范围是x≠0;
②点P(﹣3,2)在反比例函数y=﹣的图象上;
③反比例函数y=的图象,在每一个象限内,y随x的增大而增大.
A.①② B.①③ C.②③ D.①②③
【解析】解:①反比例函数y=中自变量x的取值范围是x≠0,故说法正确;
②因为﹣3×2=﹣6,故说法正确;
③因为k=3>0,反比例函数y=的图象,在每一个象限内,y随x的增大而减小,故说法错误;
故选:A.
42.(2分)(2022 海南)若反比例函数y=(k≠0)的图象经过点(2,﹣3),则它的图象也一定经过的点是( )
A.(﹣2,﹣3) B.(﹣3,﹣2) C.(1,﹣6) D.(6,1)
【解析】解:∵反比例函数y=(k≠0)的图象经过点(2,﹣3),
∴k=2×(﹣3)=﹣6,
A、﹣2×(﹣3)=6≠﹣6,故A不正确,不符合题意;
B、(﹣3)×(﹣2)=6≠﹣6,故B不正确,不符合题意;
C、1×(﹣6)=﹣6,故C正确,符合题意,
D、6×1=6≠﹣6,故D不正确,不符合题意.
故选:C.
43.(2分)(2022 武汉)已知点A(x1,y1),B(x2,y2)在反比例函数y=的图象上,且x1<0<x2,则下列结论一定正确的是( )
A.y1+y2<0 B.y1+y2>0 C.y1<y2 D.y1>y2
【解析】解:∵反比例函数y=中的6>0,
∴该双曲线位于第一、三象限,且在每一象限内y随x的增大而减小,
∵点A(x1,y1),B(x2,y2)在反比例函数y=的图象上,且x1<0<x2,
∴点A位于第三象限,点B位于第一象限,
∴y1<y2.
故选:C.
44.(2分)(2022 宿迁)如图,点A在反比例函数y=(x>0)的图象上,以OA为一边作等腰直角三角形OAB,其中∠OAB=90°,AO=AB,则线段OB长的最小值是( )
A.1 B. C.2 D.4
【解析】解:∵三角形OAB是等腰直角三角形,
∴当OB最小时,OA最小,
设A点坐标为(a,),
∴OA=,
∵≥0,
即:﹣4≥0,
∴≥4,
∵≥0,
两边同时开平方得:a﹣=0,
∴当a=时,OA有最小值,
解得a1=,a2=﹣(舍去),
∴A点坐标为(,),
∴OA=2,
∵三角形OAB是等腰直角三角形,OB为斜边,
∴OB=OA=2.
故选:C.
45.(2分)(2021 益阳)正比例函数y=2x与反比例函数y=的图象或性质的共有特征之一是( )
A.函数值y随x的增大而增大
B.图象在第一、三象限都有分布
C.图象与坐标轴有交点
D.图象经过点(2,1)
【解析】解:∵对于正比例函数y=2x,2>0,函数值y随x的增大而增大,
对于反比例函数y=,2>0,双曲线在每一象限内函数值y随x的增大而减小,
∴A选项不符合题意;
∵对于正比例函数y=2x,2>0,直线y=2x经过第一、三象限,
对于反比例函数y=,2>0,双曲线的两个分支在第一、三象限,
∴B选项符合题意;
∵对于正比例函数y=2x,它的图象经过原点,
对于反比例函数y=,它的图象与坐标轴没有交点,
∴C选项不符合题意;
∵当x=2,y=2×2=4≠1
∴正比例函数y=2x的图象不经过点(2,1).
∵当x=2时,y=,
∴反比例函数y=的图象经过(2,1),
∴D选项不符合题意.
综上,正确选项为:B.
故选:B.
46.(2分)(2021 滨州)如图,在△OAB中,∠BOA=45°,点C为边AB上一点,且BC=2AC.如果函数y=(x>0)的图象经过点B和点C,那么用下列坐标表示的点,在直线BC上的是( )
A.(﹣2019,674) B.(﹣2020,675)
C.(2021,﹣669) D.(2022,﹣670)
【解析】解:作BD⊥OA,CE⊥OA,
∵∠BOA=45°,
∴BD=OD,
设B(a,a),
∴,
∴a=3或a=﹣3(舍去),
∴BD=OD=3,
B(3,3),
∵BC=2AC.
∴AB=3AC,
∵BD⊥OA,CE⊥OA,
∴BD∥CE,
.∴△ABD∽△ACE
∵=3,
∴,
∴CE=1,
∵图象经过点C,
∴,
∴x=9,
C(9,1)
设BC的解析式为y=kx+b,
,
解得,
∴x+4,
当x=﹣2019时,y=677,
当x=﹣2020时,y=677,
当x=2021时,y=﹣669,
当x=2022时,y=﹣670,
故选:D.
47.(2分)(2021 广州)在平面直角坐标系xOy中,矩形OABC的顶点A在函数y=(x>0)的图象上,顶点C在函数y=﹣(x<0)的图象上,若顶点B的横坐标为﹣,则点A的坐标为( )
A.(,2) B.(,) C.(2,) D.(,)
【解析】解:如图,作AD⊥x轴于点D,CE⊥x轴于点E,
∵四边形OABC是矩形,
∴∠AOC=90°,
∴∠AOD+∠COE=90°,
∵∠AOD+∠OAD=90°,
∴∠COE=∠OAD,
∵∠CEO=∠ODA,
∴△COE∽△OAD,
∴=()2,,
∵S△COE=×|﹣4|=2,S△AOD==,
∴=()2,
∴=2,
∴=,
∴OE=2AD,CE=2OD,
设A(m,)(m>0),
∴C(﹣,2m),
∴OE=0﹣(﹣)=,
∵点B的横坐标为﹣,
∴m﹣(﹣)=,
整理得2m2+7m﹣4=0,
∴m1=,m2=﹣4(不符合题意,舍去),
经检验,m=是方程的解,
∴A(,2),
故选:A.
48.(2分)(2022 东营)如图,一次函数y1=k1x+b与反比例函数y2=的图象相交于A,B两点,点A的横坐标为2,点B的横坐标为﹣1,则不等式k1x+b<的解集是( )
A.﹣1<x<0或x>2 B.x<﹣1或0<x<2
C.x<﹣1或x>2 D.﹣1<x<2
【解析】解:观察函数图象可知,当﹣1<x<0或x>2时,一次函数y1=k1x+b的图象在反比例函数y2=的图象的下方,
∴不等式k1x+b<的解集为:﹣1<x<0或x>2,
故选:A.
49.(2分)(2022 无锡)一次函数y=mx+n的图象与反比例函数y=的图象交于点A、B,其中点A、B的坐标为A(﹣,﹣2m)、B(m,1),则△OAB的面积是( )
A.3 B. C. D.
【解析】解:∵点A(﹣,﹣2m)在反比例函数y=上,
∴﹣2m=,
解得:m=2,
∴点A的坐标为:(﹣,﹣4),点B的坐标为(2,1),
∴S△OAB=××5﹣××4﹣×2×1﹣×1=,
故选:D.
50.(2分)(2022 攀枝花)如图,正比例函数y=k1x与反比例函数y=的图象交于A(1,m)、B两点,当k1x≤时,x的取值范围是( )
A.﹣1≤x<0或x≥1 B.x≤﹣1或0<x≤1
C.x≤﹣1或x≥1 D.﹣1≤x<0或0<x≤1
【解析】解:∵正比例函数y=k1x与反比例函数y=的图象交于A(1,m)、B两点,
∴B(﹣1,﹣m),
由图象可知,当k1x≤时,x的取值范围是﹣1≤x<0或x≥1,
故选:A.
51.(2分)(2022 朝阳)如图,正比例函数y=ax(a为常数,且a≠0)和反比例函数y=(k为常数,且k≠0)的图象相交于A(﹣2,m)和B两点,则不等式ax>的解集为( )
A.x<﹣2或x>2 B.﹣2<x<2
C.﹣2<x<0或x>2 D.x<﹣2或0<x<2
【解析】解:∵正比例函数y=ax(a为常数,且a≠0)和反比例函数y=(k为常数,且k≠0)的图象相交于A(﹣2,m)和B两点,
∴B(2,﹣m),
∴不等式ax>的解集为x<﹣2或0<x<2,
故选:D.
52.(2分)(2022 怀化)如图,直线AB交x轴于点C,交反比例函数y=(a>1)的图象于A、B两点,过点B作BD⊥y轴,垂足为点D,若S△BCD=5,则a的值为( )
A.8 B.9 C.10 D.11
【解析】解:设点B的坐标为(m,),
∵S△BCD=5,且a>1,
∴×m×=5,
解得:a=11,
故选:D.
53.(2分)(2021 无锡)在平面直角坐标系中,O为坐标原点,点A(a,2)是反比例函数的图象上的点,连接AO并延长与反比例函数图象交于另一点B,将直线AB向下平移,与反比例函数的图象交于C、D两点.若△ABC的面积为5,则向下平移的距离是( )
A.3 B.5 C.4 D.
【解析】解:∵点A(a,2)是反比例函数的图象上的点,
∴2a=﹣2,
∴a=﹣1,
∴A(﹣1,2),
∵AB过原点,
∴B(1,﹣2),
∴AB==2,直线AB为y=﹣2x,
过C点作CD⊥AB于D,CE∥x轴交AB于E,
∵S△ABC=CD AB=5,
∴CD===,
设直线AB向左平移m个单位,
∴得y=﹣2(x+m)=﹣2x﹣2m(m>0),
∴CE=m,CD=CE sin∠CED,
作AH⊥y轴于H,
∵CE∥AH,
∴∠CED=∠OAH,
∵sin∠OAH===,
∴CD=m =,
解得m=,
∴﹣2m=﹣5,
∴向下平移的距离是5,
故选:B.
54.(2分)(2022 荆州)如图是同一直角坐标系中函数y1=2x和y2=的图象.观察图象可得不等式2x>的解集为( )
A.﹣1<x<1 B.x<﹣1或x>1
C.x<﹣1或0<x<1 D.﹣1<x<0或x>1
【解析】解:由图象,函数y1=2x和y2=的交点横坐标为﹣1,1,
∴当﹣1<x<0或x>1时,y1>y2,即2x>,
故选:D.
55.(2分)(2021 梧州)如图,在同一平面直角坐标系中,直线y=t(t为常数)与反比例函数y1=,y2=﹣的图象分别交于点A,B,连接OA,OB,则△OAB的面积为( )
A.5t B. C. D.5
【解析】解:如图,设AB交y轴于T.
∵AB⊥y轴,
∴S△OBT=,S△OAT==2,
∴S△AOB=S△OBT+S△OAT=+2=,
故选:C.
56.(2分)(2022 内江)如图,在平面直角坐标系中,点M为x轴正半轴上一点,过点M的直线l∥y轴,且直线l分别与反比例函数y=和y=的图象交于P、Q两点.若S△POQ=15,则k的值为( )
A.38 B.22 C.﹣7 D.﹣22
【解析】解:∵直线l∥y轴,
∴∠OMP=∠OMQ=90°,
∴S△OMP=×8=4,S△OMQ=﹣k.
又S△POQ=15,
∴4﹣k=15,
即k=11,
∴k=﹣22.
故选:D.
57.(2分)(2021 南通)平面直角坐标系xOy中,直线y=2x与双曲线y=(k>2)相交于A,B两点,其中点A在第一象限.设M(m,2)为双曲线y=(k>2)上一点,直线AM,BM分别交y轴于C,D两点,则OC﹣OD的值为( )
A.2 B.4 C.6 D.8
【解析】解:解法一:设A(a,2a),M(m,2),则B(﹣a,﹣2a),
设直线BM的解析式为:y=nx+b,
则,解得:,
∴直线BM的解析式为:y=x+,
∴OD=,
同理得:直线AM的解析式为:y=x+,
∴OC=,
∵a 2a=2m,
∴m=a2,
∴OC﹣OD=﹣=4;
解法二:由题意得:,
解得:,,
∵点A在第一象限,
∴A(,),B(﹣,﹣),
∵M(m,2)为双曲线y=(k>2)上一点,
∴2m=k,
∴m=,
∴M(,2),
如图,过点A作AP⊥y轴于P,过点M作ME⊥y轴于E,过点B作BF⊥y轴于F,
∴∠MED=∠BFD=90°,
∵∠EDM=∠BDF,
∴△EMD∽△FBD,
∴,即==,
∴OD==﹣2,
∵∠CPA=∠CEM=90°,∠ACP=∠ECM,
∴△CPA∽△CEM,
∴,即==,
∴OC===+2,
∴OC﹣OD=+2﹣(﹣2)=4.
解法三:取k=8,如图,则M(4,2),A(2,4),B(﹣2,﹣4),
得AM的解析式为:y=﹣x+6,BM的解析式为:y=x﹣2,
∴OC=6,OD=2,
∴OC﹣OD=6﹣2=4.
故选:B.
58.(2分)(2022 宜昌)已知经过闭合电路的电流I(单位:A)与电路的电阻R(单位:Ω)是反比例函数关系.根据下表判断a和b的大小关系为( )
I/A 5 … a … … … b … 1
R/Ω 20 30 40 50 60 70 80 90 100
A.a>b B.a≥b C.a<b D.a≤b
【解析】解:∵闭合电路的电流I(单位:A)与电路的电阻R(单位:Ω)是反比例函数关系,
∴40a=80b,
∴a=2b,
∴a>b,
故选:A.
59.(2分)(2022 宁夏)在显示汽车油箱内油量的装置模拟示意图中,电压U一定时,油箱中浮子随油面下降而落下,带动滑杆使滑动变阻器滑片向上移动,从而改变电路中的电流,电流表的示数对应油量体积,把电流表刻度改为相应油量体积数,由此知道油箱里剩余油量.在不考虑其他因素的条件下,油箱中油的体积V与电路中总电阻R总(R总=R+R0)是反比例关系,电流I与R总也是反比例关系,则I与V的函数关系是( )
A.反比例函数 B.正比例函数
C.二次函数 D.以上答案都不对
【解析】解:由油箱中油的体积V与电路中总电阻R总是反比例关系,设V R总=k(k为常数),
由电流I与R总是反比例关系,设I R总=k'(k为常数),
∴=,
∴I=V(为常数),
∴I与V的函数关系是正比例函数,
故选:B.
60.(2分)(2022 丽水)已知电灯电路两端的电压U为220V,通过灯泡的电流强度I(A)的最大限度不得超过0.11A.设选用灯泡的电阻为R(Ω),下列说法正确的是( )
A.R至少2000Ω B.R至多2000Ω C.R至少24.2Ω D.R至多24.2Ω
【解析】解:∵电压U一定时,电流强度I(A)与灯泡的电阻为R(Ω)成反比例,
∴I=.
∵已知电灯电路两端的电压U为220V,
∴I=.
∵通过灯泡的电流强度I(A)的最大限度不得超过0.11A,
∴≤0.11,
∴R≥2000.
故选:A.
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
