初中数学青岛版 七年级下册 8.1 角的表示 同步课件(共42张PPT)
文档属性
| 名称 | 初中数学青岛版 七年级下册 8.1 角的表示 同步课件(共42张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 50.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-11 14:43:15 | ||
图片预览










文档简介
(共42张PPT)
第 8 章 角
青岛版 七年级下册
8 . 1
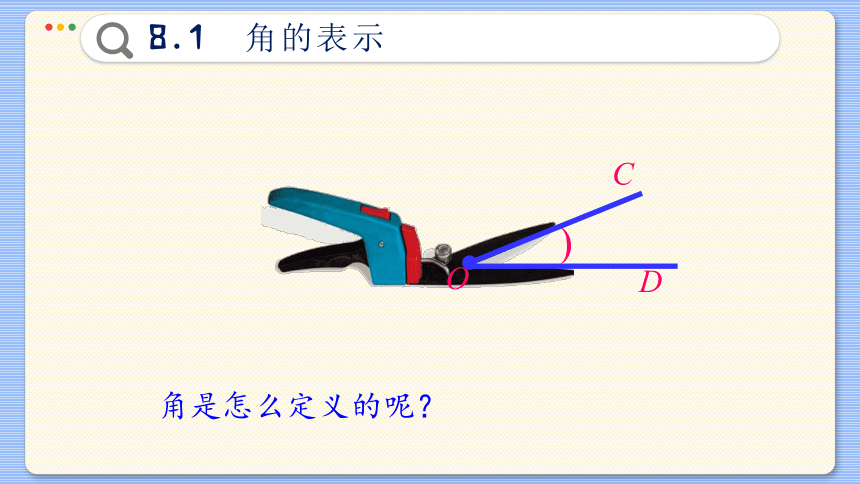
角的表示
交流与发现
你还记得以前学过的角吗 从铁桥、梯子、标志牌的图片中,你看到角的形象了吗
铁 桥
梯 子
标志牌
你还能在生活中找到类似的例子吗
这些角的形象有什么共同特点
与同学交流.
)
O
C
●
D
角是怎么定义的呢?
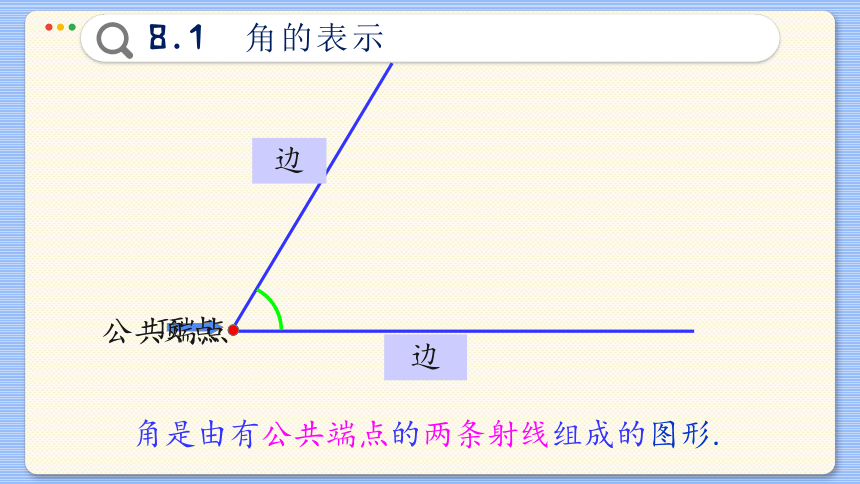
公共端点
顶点
射线
射线
边
边
角是由有公共端点的两条射线组成的图形.
有公共端点的两条射线组成的图形叫做角.
这个公共端点叫做角的顶点,
这两条射线叫做角的边.
在图中,点O是角的顶点,射线OA与 OB是角的边.
角用符号“∠”和三个大写英文字母表示.
图中的角可以记作∠AOB或∠BOA.
表示顶点的字母O必须写在中间,
读作“角AOB”或“角BOA”.
如果在顶点处只有一个角,也可以只用表示这个顶点的字母来表示这个角.
如图中的∠AOB也可记作∠O.
为了方便,有时还可以在靠近顶点处画上弧线,并用一个数字或一个小写希腊字母表示一个角.
例如,图中的∠1,∠2或∠α,∠β等.
你能总结出角有几种表示方法吗?
角有四种表示方法:
(1) 用三个大写英文字母表示角;
(2) 用一个大写英文字母表示角;
(3) 用一个阿拉伯数字表示角;
(4) 用一个希腊字母表示角.
观察上面钟表指针的转动,你发现了什么?
观察与思考
(1) 从台秤指针的转动、圆规的张开、汽车雨刷的摆动中,你能发现角的形象吗 与同学交流.
台秤
圆规
雨刷
(2) 观察,当射线 OA绕着端点O旋转时,它的起始位置 OA 和终止位置 OB组成了一个什么图形
O
A
B
起始位置的射线,叫做角的始边,
终止位置的射线,叫做角的终边.
角的始边
角的终边
角也可以看做是由一条射线绕着端点从起始位置旋转到终止位置所成的图形.
射线旋转时经过的平面部分是角的内部.
O
A
B
(3) 观察图,射线OA绕端点O旋转,当终止位置OB 与起始位置OA成一条直线时,所成的角是平角.
O
A
(B)
观察图,射线OA继续按逆时针方向旋转,当终止位置 OB与起始位置 OA重合时,所成的角是周角.
当角的始边和终边恰好成一条直线时,所成的角叫做平角;
当射线旋转一周回到起始位置时,所成的角叫做周角.
在右图中,点D在AB上.
(1) 以点C为顶点的角有哪几个?把它们分别写出来.
(2) 图中哪些角可以用一个字母表示?
(3) 数一数,图中共有多少个角?
例 1
以点C为顶点的角有哪几个?把它们分别写出来.
(2) 图中哪些角可以用一个字母表示?
以点C为顶点的角有∠ACB, ∠ACD, ∠BCD;
可以只用一个字母表示的角有∠A, ∠B;
(3) 数一数,图中共有多少个角?
图中共有7个角:
∠A, ∠B, ∠ACB,∠ACD,
∠BCD, ∠ADC,∠BDC.
随堂练习
1.下列4个图形中,能用∠1,∠AOB,∠O 三种方法表示同一个角的图形是( )
B
2. 请将图中的角用不同方法表示出来,并填写下表:
∠ABE
∠1 ∠2 ∠3
∠B
∠C或∠ACD
∠BED
∠A或∠BAC
3. 如图所示,用三个大写字母表示角,
∠1为_______,∠2为_______,
∠3为_______,∠4为_______ .
∠AEC
∠BED
∠ABC
∠BCE
归纳总结
角是由两条具有公共端点的射线组成的图形,
角的要素为顶点和边,
角的大小不随边的长短而变化,即与边无关.
1. 角的定义
2. 角的表示方法 (角有四种表示方法:)
①可用三个大写字母表示;
②可用一个数字来表示;
③也可用一个希腊字母来表示;
④可用一个大写字母来表示.
特别的,必须是在不引起混淆的情况下,才用一个大写字母来表示.
练 习
1. 如图,分别指出以射线OA,OB,OC为一边的角,并把它们表示出来.
以射线OA为一边的角:∠AOB,∠AOC,∠AOD;
以射线OB为一边的角:∠AOB,∠BOC,∠BOD;
以射线OC为一边的角:∠AOC,∠BOC,∠COD.
2. 如图,分别用三个大写字母表示∠1,∠2,∠3,∠4,∠5.
∠BAO为∠1, ∠DAO为∠2, ∠ABO为∠3, ∠DOC为∠4, ∠OCB为∠5.
3. 请你举出几个由旋转产生的角的实例.
如钟表上指针的转动,酒店的转门,风车,荡秋千,电风扇等.
习题 8.1
复习与巩固
1. 如图,分别用三个大写字母表示图中的∠1, ∠2, ∠3.
∠DAC为∠1, ∠CDE为∠2, ∠ACB为∠3.
2. 下面各图中哪些角可以只用一个大写字母表示 哪些角必须用三个大写字母表示 把它们分别写出来.
∠AOB,
∠BOC,
∠AOC.
∠A,
∠C,
∠AOD,
∠AOC
∠BOC
∠BOD.
∠AOC,
∠AOB.
∠B, ∠C,
∠BAC,∠BAD,
∠DAC,∠ADB,
∠ADC.
拓展与延伸
3. 数一数,图中共有多少个角?把它们分别表示出来.
以A为顶点的角有3个,以B为顶点的角有3个,
以C为顶点的角有3个,以D为顶点的角有3个,
以O为顶点的角有6个.
共有18个角,它们分别是∠BAD,∠BAC,∠DAC, ∠ABC,∠ABD,∠CBD, ∠BCD,∠BCA,∠DCA, ∠ADC,∠ADB,∠CDB, ∠AOD,∠AOB,∠COD, ∠BOC,∠BOD,∠AOC.
探索与创新
4. 一个正常走动的时钟,时针从某一时刻所在的位置开始,旋转一个平角和一个周角,各需要多少时间?对于分针,回答同样的问题.
∵时针旋转一小时转动30°.
∴时针旋转出一个平角需要6小时,时针旋转出一个周角需要12小时.
同理,分针旋转出一个平角需要30分钟,时针旋转出一个周角需要60分钟
本课结束!
第 8 章 角
青岛版 七年级下册
8 . 1
角的表示
交流与发现
你还记得以前学过的角吗 从铁桥、梯子、标志牌的图片中,你看到角的形象了吗
铁 桥
梯 子
标志牌
你还能在生活中找到类似的例子吗
这些角的形象有什么共同特点
与同学交流.
)
O
C
●
D
角是怎么定义的呢?
公共端点
顶点
射线
射线
边
边
角是由有公共端点的两条射线组成的图形.
有公共端点的两条射线组成的图形叫做角.
这个公共端点叫做角的顶点,
这两条射线叫做角的边.
在图中,点O是角的顶点,射线OA与 OB是角的边.
角用符号“∠”和三个大写英文字母表示.
图中的角可以记作∠AOB或∠BOA.
表示顶点的字母O必须写在中间,
读作“角AOB”或“角BOA”.
如果在顶点处只有一个角,也可以只用表示这个顶点的字母来表示这个角.
如图中的∠AOB也可记作∠O.
为了方便,有时还可以在靠近顶点处画上弧线,并用一个数字或一个小写希腊字母表示一个角.
例如,图中的∠1,∠2或∠α,∠β等.
你能总结出角有几种表示方法吗?
角有四种表示方法:
(1) 用三个大写英文字母表示角;
(2) 用一个大写英文字母表示角;
(3) 用一个阿拉伯数字表示角;
(4) 用一个希腊字母表示角.
观察上面钟表指针的转动,你发现了什么?
观察与思考
(1) 从台秤指针的转动、圆规的张开、汽车雨刷的摆动中,你能发现角的形象吗 与同学交流.
台秤
圆规
雨刷
(2) 观察,当射线 OA绕着端点O旋转时,它的起始位置 OA 和终止位置 OB组成了一个什么图形
O
A
B
起始位置的射线,叫做角的始边,
终止位置的射线,叫做角的终边.
角的始边
角的终边
角也可以看做是由一条射线绕着端点从起始位置旋转到终止位置所成的图形.
射线旋转时经过的平面部分是角的内部.
O
A
B
(3) 观察图,射线OA绕端点O旋转,当终止位置OB 与起始位置OA成一条直线时,所成的角是平角.
O
A
(B)
观察图,射线OA继续按逆时针方向旋转,当终止位置 OB与起始位置 OA重合时,所成的角是周角.
当角的始边和终边恰好成一条直线时,所成的角叫做平角;
当射线旋转一周回到起始位置时,所成的角叫做周角.
在右图中,点D在AB上.
(1) 以点C为顶点的角有哪几个?把它们分别写出来.
(2) 图中哪些角可以用一个字母表示?
(3) 数一数,图中共有多少个角?
例 1
以点C为顶点的角有哪几个?把它们分别写出来.
(2) 图中哪些角可以用一个字母表示?
以点C为顶点的角有∠ACB, ∠ACD, ∠BCD;
可以只用一个字母表示的角有∠A, ∠B;
(3) 数一数,图中共有多少个角?
图中共有7个角:
∠A, ∠B, ∠ACB,∠ACD,
∠BCD, ∠ADC,∠BDC.
随堂练习
1.下列4个图形中,能用∠1,∠AOB,∠O 三种方法表示同一个角的图形是( )
B
2. 请将图中的角用不同方法表示出来,并填写下表:
∠ABE
∠1 ∠2 ∠3
∠B
∠C或∠ACD
∠BED
∠A或∠BAC
3. 如图所示,用三个大写字母表示角,
∠1为_______,∠2为_______,
∠3为_______,∠4为_______ .
∠AEC
∠BED
∠ABC
∠BCE
归纳总结
角是由两条具有公共端点的射线组成的图形,
角的要素为顶点和边,
角的大小不随边的长短而变化,即与边无关.
1. 角的定义
2. 角的表示方法 (角有四种表示方法:)
①可用三个大写字母表示;
②可用一个数字来表示;
③也可用一个希腊字母来表示;
④可用一个大写字母来表示.
特别的,必须是在不引起混淆的情况下,才用一个大写字母来表示.
练 习
1. 如图,分别指出以射线OA,OB,OC为一边的角,并把它们表示出来.
以射线OA为一边的角:∠AOB,∠AOC,∠AOD;
以射线OB为一边的角:∠AOB,∠BOC,∠BOD;
以射线OC为一边的角:∠AOC,∠BOC,∠COD.
2. 如图,分别用三个大写字母表示∠1,∠2,∠3,∠4,∠5.
∠BAO为∠1, ∠DAO为∠2, ∠ABO为∠3, ∠DOC为∠4, ∠OCB为∠5.
3. 请你举出几个由旋转产生的角的实例.
如钟表上指针的转动,酒店的转门,风车,荡秋千,电风扇等.
习题 8.1
复习与巩固
1. 如图,分别用三个大写字母表示图中的∠1, ∠2, ∠3.
∠DAC为∠1, ∠CDE为∠2, ∠ACB为∠3.
2. 下面各图中哪些角可以只用一个大写字母表示 哪些角必须用三个大写字母表示 把它们分别写出来.
∠AOB,
∠BOC,
∠AOC.
∠A,
∠C,
∠AOD,
∠AOC
∠BOC
∠BOD.
∠AOC,
∠AOB.
∠B, ∠C,
∠BAC,∠BAD,
∠DAC,∠ADB,
∠ADC.
拓展与延伸
3. 数一数,图中共有多少个角?把它们分别表示出来.
以A为顶点的角有3个,以B为顶点的角有3个,
以C为顶点的角有3个,以D为顶点的角有3个,
以O为顶点的角有6个.
共有18个角,它们分别是∠BAD,∠BAC,∠DAC, ∠ABC,∠ABD,∠CBD, ∠BCD,∠BCA,∠DCA, ∠ADC,∠ADB,∠CDB, ∠AOD,∠AOB,∠COD, ∠BOC,∠BOD,∠AOC.
探索与创新
4. 一个正常走动的时钟,时针从某一时刻所在的位置开始,旋转一个平角和一个周角,各需要多少时间?对于分针,回答同样的问题.
∵时针旋转一小时转动30°.
∴时针旋转出一个平角需要6小时,时针旋转出一个周角需要12小时.
同理,分针旋转出一个平角需要30分钟,时针旋转出一个周角需要60分钟
本课结束!
同课章节目录
- 第8章 角
- 8.1 角的表示
- 8.2 角的比较
- 8.3 角的度量
- 8.4 对顶角
- 8.5 垂直
- 第9章 平行线
- 9.1 同位角、内错角、同旁内角
- 9.2 平行线和它的画法
- 9.3 平行线的性质
- 9.4 平行线的判定
- 第10章 一次方程组
- 10.1 认识二元一次方程组
- 10.2 二元一次方程组的解法
- 10.3 三元一次方程组
- 10.4 列方程组解应用题
- 第11章 整式的乘除
- 11.1 同底数幂的乘法
- 11.2 积的乘方与幂的乘方
- 11.3 单项式的乘法
- 11.4 多项式乘多项式
- 11.5 同底数幂的除法
- 11.6 零指数幂与负整数指数幂
- 第12章 乘法公式与因式分解
- 12.1 平方差公式
- 12.2 完全平方公式
- 12.3 用提公因式法进行因式分解
- 12.4 用公式法进行因式分解
- 第13章 平面图形的认识
- 13.1 三角形
- 13.2 多边形
- 13.3 圆
- 第14章 位置与坐标
- 14.1 用有序数对表示位置
- 14.2 平面直角坐标系
- 14.3 直角坐标系中的图形
- 14.4 用方向和距离描述两个物体的相对位置
