二分法[上学期]
图片预览




文档简介
课件10张PPT。用二分法求方程的近似解问题情境CCTV2“幸运52”片段 :
主持人李咏说道:猜一猜这架家用型数码相机的价格.观众甲:2000!李咏:高了! 观众乙:1000! 李咏:低了! 观众丙:1500! 李咏:还是低了!········
问题2:你知道这件商品的价格在什么范围内吗?
问题3:若接下来让你猜的话,你会猜多少价格比较合理呢?答案:1500至2000之间学生活动问题4:方程
的解是什么? 若不用求根公式,如何
求方程 的一个近似
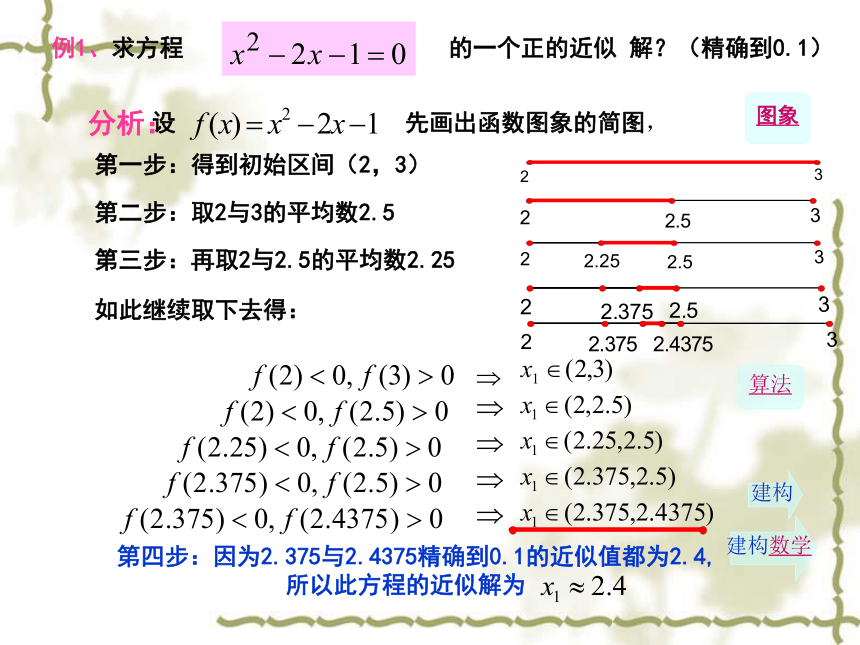
解呢?答案:例1、求方程 的一个正的近似 解?(精确到0.1)第二步:取2与3的平均数2.5 第三步:再取2与2.5的平均数2.25 如此继续取下去得: 第四步:因为2.375与2.4375精确到0.1的近似值都为2.4,
所以此方程的近似解为 图象算法第一步:得到初始区间(2,3)设 先画出函数图象的简图,分析:建构数学建构1.二分法的描述:
[建构数学] 对于区间[a,b]上连续不断、且f(a)f(b)<0的函数y=f(x),通过不断地把函数f(x)的零点所在的区间
一分为二,使区间的两个端点逐步逼近零点,进而得到零点近似值的方法叫做二分法.
2.用二分法求一元方程f(x)=0的近似解的基本步骤:
[建构数学]第一步 确定初始区间[a,b],验证f(a)f(b)<0 第二步 求区间[a,b]两端点的平均值x1,
第三步 计算f(x1) 并判断:(1)如果f(x1)=0,则x1就是f(x)的零点,计算终止; (2)如果f(a)f(x1)<0,则零点 ,否则零点
。第四步 重复步骤2~3,直至所得区间的两端点在要
求的精确度下取得的近似值相等,则零点
的近似值为所得区间内的任一数。例1例二、利用计算器,求方程 的近似解(精确到0.1) 数学应用 因为2.5625与2.625精确到0.1的近似值都为2.6,所以原方程的近似解为解:设f(x)=lgx+x-3用计算器计算,得:
拓展当堂反馈1、求方程 在区
间(0,1)内的近似解(精
确到0.1)
当堂反馈1、解:设, 方程满足条件的解为 ,用计算器计算得:
因为0.3125和0.34375精确到0.1的近似值都是0.3,
所以答案:知识与技能:
理解用二分法求方程的近似解, 学会借助
计算器用二分法求相应方程的近似解.
学习目标情感、态度和世界观
正面解决问题困难时,可以通过迂回的方法解决.
体会二分法等算法的数学应用价值,感受数学美.
主持人李咏说道:猜一猜这架家用型数码相机的价格.观众甲:2000!李咏:高了! 观众乙:1000! 李咏:低了! 观众丙:1500! 李咏:还是低了!········
问题2:你知道这件商品的价格在什么范围内吗?
问题3:若接下来让你猜的话,你会猜多少价格比较合理呢?答案:1500至2000之间学生活动问题4:方程
的解是什么? 若不用求根公式,如何
求方程 的一个近似
解呢?答案:例1、求方程 的一个正的近似 解?(精确到0.1)第二步:取2与3的平均数2.5 第三步:再取2与2.5的平均数2.25 如此继续取下去得: 第四步:因为2.375与2.4375精确到0.1的近似值都为2.4,
所以此方程的近似解为 图象算法第一步:得到初始区间(2,3)设 先画出函数图象的简图,分析:建构数学建构1.二分法的描述:
[建构数学] 对于区间[a,b]上连续不断、且f(a)f(b)<0的函数y=f(x),通过不断地把函数f(x)的零点所在的区间
一分为二,使区间的两个端点逐步逼近零点,进而得到零点近似值的方法叫做二分法.
2.用二分法求一元方程f(x)=0的近似解的基本步骤:
[建构数学]第一步 确定初始区间[a,b],验证f(a)f(b)<0 第二步 求区间[a,b]两端点的平均值x1,
第三步 计算f(x1) 并判断:(1)如果f(x1)=0,则x1就是f(x)的零点,计算终止; (2)如果f(a)f(x1)<0,则零点 ,否则零点
。第四步 重复步骤2~3,直至所得区间的两端点在要
求的精确度下取得的近似值相等,则零点
的近似值为所得区间内的任一数。例1例二、利用计算器,求方程 的近似解(精确到0.1) 数学应用 因为2.5625与2.625精确到0.1的近似值都为2.6,所以原方程的近似解为解:设f(x)=lgx+x-3用计算器计算,得:
拓展当堂反馈1、求方程 在区
间(0,1)内的近似解(精
确到0.1)
当堂反馈1、解:设, 方程满足条件的解为 ,用计算器计算得:
因为0.3125和0.34375精确到0.1的近似值都是0.3,
所以答案:知识与技能:
理解用二分法求方程的近似解, 学会借助
计算器用二分法求相应方程的近似解.
学习目标情感、态度和世界观
正面解决问题困难时,可以通过迂回的方法解决.
体会二分法等算法的数学应用价值,感受数学美.
