辽宁省抚顺市六校联合体2013-2014学年高二下学期期末考试数学(理)试题
文档属性
| 名称 | 辽宁省抚顺市六校联合体2013-2014学年高二下学期期末考试数学(理)试题 | 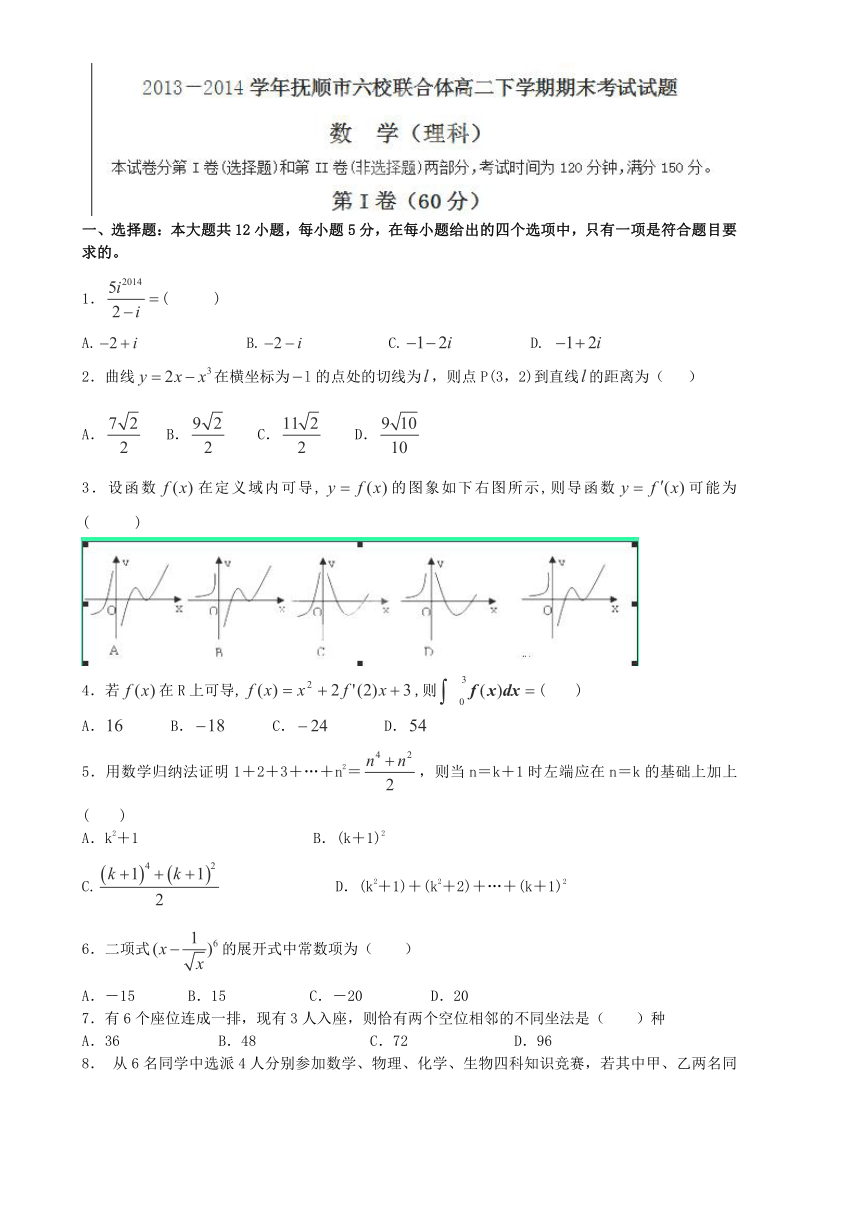 | |
| 格式 | zip | ||
| 文件大小 | 258.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-07-17 18:57:52 | ||
图片预览




文档简介
一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.( )
A. B. C. D.
2.曲线在横坐标为l的点处的切线为,则点P(3,2)到直线的距离为( )
A. B. C. D.
3.设函数在定义域内可导,的图象如下右图所示,则导函数可能为( )
4.若在R上可导,,则( )
A. B. C. D.
5.用数学归纳法证明1+2+3+…+n2=,则当n=k+1时左端应在n=k的基础上加上( )
A.k2+1 B.(k+1)2
C. D.(k2+1)+(k2+2)+…+(k+1)2
6.二项式的展开式中常数项为( )
A.-15 B.15 C.-20 D.20
7.有6个座位连成一排,现有3人入座,则恰有两个空位相邻的不同坐法是( )种
A.36 B.48 C.72 D.96
8. 从6名同学中选派4人分别参加数学、物理、化学、生物四科知识竞赛,若其中甲、乙两名同学不能参加生物竞赛,则选派方案共有( )
A.180种 B.280种 C. 96种 D.240种
9.将二颗骰子各掷一次,设事件A=“二个点数不相同”,B=“至少出现一个6点”,则概率 等于( )
A. B. C. D.
10.甲、乙同时炮击一架敌机,已知甲击中敌机的概率为,乙击中敌机的概率为,敌机被击中的概率为( )
A. B. C. D.
11.已知随机变量服从正态分布,,则的值等于( )
A.0.1 B.0.2 C.0.4 D.0.6
12.设随机变量ξ~,又η=5ξ,则Eη和Dη的值分别是( )
A、和 B、和 C、和 D、和
第Ⅱ卷(90分)
二、填空题:本大题共5小题。
13.若n的展开式中含x的项为第6项,设(1-3x)n=a0+a1x+a2x2+…+anxn,则a1+a2+…+an的值为________.
14.有甲、乙、丙三项任务,甲需2人承担,乙、丙各需1人承担,从10人中选派4人承担这项任务,不同的选法有________.
15.观察各式:,则依次类推可得 ;
16.大小相同的4个小球上分别写有数字1,2,3,4,从这4个小球中随机抽取2个小球,则取出的2个小球上的数字之和为奇数的概率为`________
三、解答题
17.(本题12分)(1)用反证法证明:在一个三角形中,至少有一个内角大于或等于;
(2)已知,试用分析法证明:.
18.(本题12分).从名男生和名女生中任选人参加演讲比赛,
①求所选人都是男生的概率;
②求所选人恰有名女生的概率;
③求所选人中至少有名女生的概率。
19.(本题12分)已知甲盒内有大小相同的1个红球和3个黑球, 乙盒内有大小相同的2个红球和4个黑球,现从甲、乙两个盒内各任取2个球.
(Ⅰ)求取出的4个球均为黑球的概率;
(Ⅱ)求取出的4个球中恰有1个红球的概率;
(Ⅲ)设为取出的4个球中红球的个数,求的分布列和数学期望
20.(本题12分)函数
(1)a=0时,求f(x)最小值;
(2)若f(x)在是单调减函数,求a的取值范围.
21.(本题12分)为了解某班学生关注NBA是否与性别有关,对本班48人进行了问卷调查得到如下的列联表:
关注NBA 不关注NBA 合 计
男 生 6
女 生 10
合 计 48
已知在全班48人中随机抽取1人,抽到关注NBA的学生的概率为2/3
⑴请将上面列连表补充完整,并判断是否有的把握认为关注NBA与性别有关?
⑵现从女生中抽取2人进一步调查,设其中关注NBA的女生人数为X,求X的分布列与数学期望。
附:,其中
0.15 0.10 0.05 0.025 0.010
2.072 2.706 3.841 5.024 6.635
考生在题(22)(23)(24)中任选一题作答,如果多做,则按所做的的第一题计分.做题时用2B铅笔在答题卡上把所选题目对应的题号涂黑.
(22)(本小题满分10分)选修4-1:几何证明选讲
如图所示,△ABC内接于⊙O,AB=AC,直线XY切⊙O于点C,BD∥XY,AC、BD相交于E.
(1)求证:△ABE≌△ACD;
(2)若AB=6 cm,BC=4 cm,求AE的长.
23.(本小题满分10分)《选修4-4:坐标系与参数方程》
已知某圆的极坐标方程是,求
(1)求圆的普通方程和一个参数方程;
(2)圆上所有点中的最大值和最小值.
(24) (本小题满分10分)选修4—5:不等式选讲
已知函数
(1)求不等式的解集;
(2)若关于的不等式的解集非空,求实数的取值范围.
19.(Ⅰ)设“从甲盒内取出的2个球均为黑球”为事件,
“从乙盒内取出的2个球均为黑球”为事件.
由于事件相互独立,且,. 2分
故取出的4个球均为黑球的概率为. 4分
(Ⅱ) 设“从甲盒内取出的2个球均为黑球;从乙盒内取出的2个球中,1个是红球,1个是黑球”为事件,“从甲盒内取出的2个球中,1个是红球,1个是黑球;从乙盒内取出的2个球均为黑球”为事件.则
20.解:(1)时,, 3分
时时,
∴f(x)在(0,1)单减,在单增, 5分
时有最小值1 6分
(2),在为减函数,则,即,当恒成立,∴最小值 9分
令,则,
12分
21.解(1)将列联表补充完整有:
所以6·(6-AE)=16.所以AE= cm. 10分
23.解:(1)普通方程:x2+y2-4x-4y+6=0 2分
参数方程:
(θ为参数) 4分
(2) 5分
令S=sinθ+COSθ=t∈, 则2sinθcosθ=t2-1
所以xy=t2+2t+3 6分
当t=-时,最小值是1; 8分
1.( )
A. B. C. D.
2.曲线在横坐标为l的点处的切线为,则点P(3,2)到直线的距离为( )
A. B. C. D.
3.设函数在定义域内可导,的图象如下右图所示,则导函数可能为( )
4.若在R上可导,,则( )
A. B. C. D.
5.用数学归纳法证明1+2+3+…+n2=,则当n=k+1时左端应在n=k的基础上加上( )
A.k2+1 B.(k+1)2
C. D.(k2+1)+(k2+2)+…+(k+1)2
6.二项式的展开式中常数项为( )
A.-15 B.15 C.-20 D.20
7.有6个座位连成一排,现有3人入座,则恰有两个空位相邻的不同坐法是( )种
A.36 B.48 C.72 D.96
8. 从6名同学中选派4人分别参加数学、物理、化学、生物四科知识竞赛,若其中甲、乙两名同学不能参加生物竞赛,则选派方案共有( )
A.180种 B.280种 C. 96种 D.240种
9.将二颗骰子各掷一次,设事件A=“二个点数不相同”,B=“至少出现一个6点”,则概率 等于( )
A. B. C. D.
10.甲、乙同时炮击一架敌机,已知甲击中敌机的概率为,乙击中敌机的概率为,敌机被击中的概率为( )
A. B. C. D.
11.已知随机变量服从正态分布,,则的值等于( )
A.0.1 B.0.2 C.0.4 D.0.6
12.设随机变量ξ~,又η=5ξ,则Eη和Dη的值分别是( )
A、和 B、和 C、和 D、和
第Ⅱ卷(90分)
二、填空题:本大题共5小题。
13.若n的展开式中含x的项为第6项,设(1-3x)n=a0+a1x+a2x2+…+anxn,则a1+a2+…+an的值为________.
14.有甲、乙、丙三项任务,甲需2人承担,乙、丙各需1人承担,从10人中选派4人承担这项任务,不同的选法有________.
15.观察各式:,则依次类推可得 ;
16.大小相同的4个小球上分别写有数字1,2,3,4,从这4个小球中随机抽取2个小球,则取出的2个小球上的数字之和为奇数的概率为`________
三、解答题
17.(本题12分)(1)用反证法证明:在一个三角形中,至少有一个内角大于或等于;
(2)已知,试用分析法证明:.
18.(本题12分).从名男生和名女生中任选人参加演讲比赛,
①求所选人都是男生的概率;
②求所选人恰有名女生的概率;
③求所选人中至少有名女生的概率。
19.(本题12分)已知甲盒内有大小相同的1个红球和3个黑球, 乙盒内有大小相同的2个红球和4个黑球,现从甲、乙两个盒内各任取2个球.
(Ⅰ)求取出的4个球均为黑球的概率;
(Ⅱ)求取出的4个球中恰有1个红球的概率;
(Ⅲ)设为取出的4个球中红球的个数,求的分布列和数学期望
20.(本题12分)函数
(1)a=0时,求f(x)最小值;
(2)若f(x)在是单调减函数,求a的取值范围.
21.(本题12分)为了解某班学生关注NBA是否与性别有关,对本班48人进行了问卷调查得到如下的列联表:
关注NBA 不关注NBA 合 计
男 生 6
女 生 10
合 计 48
已知在全班48人中随机抽取1人,抽到关注NBA的学生的概率为2/3
⑴请将上面列连表补充完整,并判断是否有的把握认为关注NBA与性别有关?
⑵现从女生中抽取2人进一步调查,设其中关注NBA的女生人数为X,求X的分布列与数学期望。
附:,其中
0.15 0.10 0.05 0.025 0.010
2.072 2.706 3.841 5.024 6.635
考生在题(22)(23)(24)中任选一题作答,如果多做,则按所做的的第一题计分.做题时用2B铅笔在答题卡上把所选题目对应的题号涂黑.
(22)(本小题满分10分)选修4-1:几何证明选讲
如图所示,△ABC内接于⊙O,AB=AC,直线XY切⊙O于点C,BD∥XY,AC、BD相交于E.
(1)求证:△ABE≌△ACD;
(2)若AB=6 cm,BC=4 cm,求AE的长.
23.(本小题满分10分)《选修4-4:坐标系与参数方程》
已知某圆的极坐标方程是,求
(1)求圆的普通方程和一个参数方程;
(2)圆上所有点中的最大值和最小值.
(24) (本小题满分10分)选修4—5:不等式选讲
已知函数
(1)求不等式的解集;
(2)若关于的不等式的解集非空,求实数的取值范围.
19.(Ⅰ)设“从甲盒内取出的2个球均为黑球”为事件,
“从乙盒内取出的2个球均为黑球”为事件.
由于事件相互独立,且,. 2分
故取出的4个球均为黑球的概率为. 4分
(Ⅱ) 设“从甲盒内取出的2个球均为黑球;从乙盒内取出的2个球中,1个是红球,1个是黑球”为事件,“从甲盒内取出的2个球中,1个是红球,1个是黑球;从乙盒内取出的2个球均为黑球”为事件.则
20.解:(1)时,, 3分
时时,
∴f(x)在(0,1)单减,在单增, 5分
时有最小值1 6分
(2),在为减函数,则,即,当恒成立,∴最小值 9分
令,则,
12分
21.解(1)将列联表补充完整有:
所以6·(6-AE)=16.所以AE= cm. 10分
23.解:(1)普通方程:x2+y2-4x-4y+6=0 2分
参数方程:
(θ为参数) 4分
(2) 5分
令S=sinθ+COSθ=t∈, 则2sinθcosθ=t2-1
所以xy=t2+2t+3 6分
当t=-时,最小值是1; 8分
同课章节目录
