初中数学青岛版 七年级下册9.1 同位角、内错角、同旁内角课件(共40张PPT)
文档属性
| 名称 | 初中数学青岛版 七年级下册9.1 同位角、内错角、同旁内角课件(共40张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 60.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-11 19:02:01 | ||
图片预览











文档简介
(共40张PPT)
第 9 章 平行线
青岛版 七年级下册
9 . 1
同位角、内错角、同旁内角
观察与思考
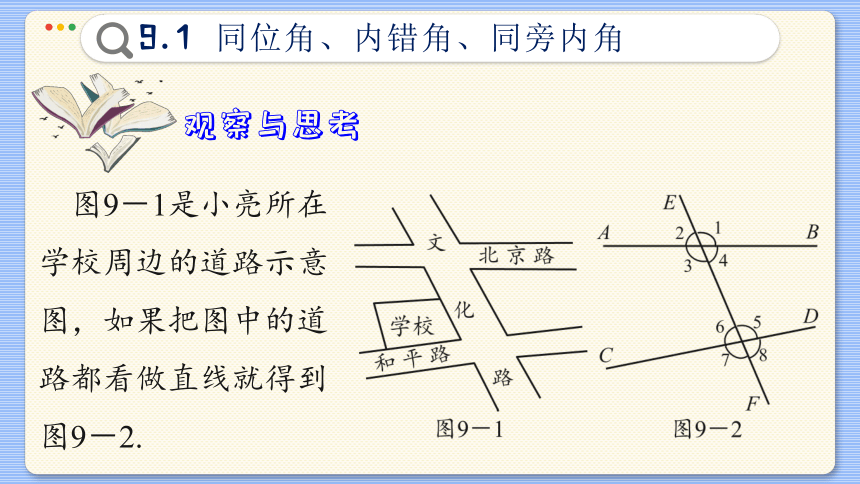
图9-1是小亮所在学校周边的道路示意图,如果把图中的道路都看做直线就得到图9-2.
(1) 在图9-2中,直线AB,CD被直线EF所截,一共形成哪几个角
∠1, ∠2,∠3,∠4, ∠5,∠6,∠7, ∠8,共8个角.
(2) 观察∠1与∠5,它们有怎样的位置关系
∠1与∠5分别在直线AB与CD的同侧,并且都在直线EF的同旁,
具有这种位置关系的一对角叫做同位角.
同样地,∠2与∠6也是同位角,除此之外,图 9-2中还有其他的同位角吗 如果有,请你指出来.
∠3与∠7,
∠4与∠8
(3) 观察∠3与∠5,它们有怎样的位置关系
∠3与∠5都在直线AB,CD之间,并且分别在直线EF的两旁,
具有这种位置关系的一对角叫做内错角.
除∠3与∠5之外,图9-2中还有其他的内错角吗
∠4与∠6,
(4) 观察∠4与∠5,它们有怎样的位置关系
∠4与∠5都在直线AB,CD之间,并且都在直线 EF的同旁,
具有这种位置关系的一对角叫做同旁内角 .
除∠4与∠5之外,图9-2中还有其他的同旁内角吗
∠3与∠6,
在右图中,直线EF,GH被直线AB所截,哪几对角是同位角 哪几对角是内错角 哪几对角是同旁内角
例 1
解:∠ACF与∠ADH,∠FCB与
∠HDB,∠ACE与∠ADG,
∠ECB与∠GDB分别是同位角;
∠FCB与∠ADG, ∠ECB与∠ADH分别是内错角;
∠FCB与∠ADH, ∠ECB与∠ADG分别是同旁内角
例 2
在右图中,直线a,b被直线l所截.
(1) ∠3与哪个角是同位角
∠3与∠7是同位角.
(2) 如果∠1=∠5,那么∠7和∠8分别与∠1有什么数量关系 说明理由.
∠7与∠1相等.
理由是:
∵∠1 = ∠5,而∠7与∠5是对顶角,∠7=∠5,
∴∠7 = ∠1.
(2) 如果∠1=∠5,那么∠7和∠8分别与∠1有什么数量关系 说明理由.
∠8与∠1互补.
理由是:
∵∠1 =∠5,∠8与∠5互补,∴∠8与∠1互补.
随堂练习
1. 如图:∠1与∠2是同位角吗?
是
不是
2. 如图:∠1与∠2是内错角吗?
是
不是
3.如图:∠1与∠2是同旁内角吗?
是
不是
归纳总结
主要内容:两条直线被第三条直线所截而产生的三种角——同位角、内错角、同旁内角.
1.三种角产生的条件及位置特征;
2.判断时应先找到“截线”,再找另外两直线,然后根据角的位置决定是哪一种角.
3.当图形复杂时可把暂时不需要的线段、角等遮住,也可采用图形分解法、图形涂色法以排除干扰.
练 习
1. 如图,直线DE与∠ABC的边BC相交于点P. 视直线AB,DE被直线BC所截, ∠1与∠2,∠1与∠3,∠1与∠4分别是什么角
∠1和∠2是同旁内角
∠1和∠3是内错角
∠1和∠4是同位角
2. 如图,直线AB,CD 被直线 EF所截,在所标出的角中,哪几对角是同位角 哪
几对角是内错角 哪几对角是
同旁内角 类似地,你能讨论
直线 EF,GH被直线AB所截形
成的角的位置关系吗
直线AB、CD被直线EF所截,在所标出的角中∠1和∠3是同位角;
∠1和∠5,∠4和∠2是内错角;
∠2和∠5,∠1和∠4是同旁内角;
直线DF、GH被直线AB所截,在所标出的角中∠2和∠6是同位角;
∠1和∠7是内错角;
∠1和∠6是同旁内角.
习题 9.1
复习与巩固
1.如图①②,直线a,b被直线l所截,在图中已标出的角中,分别找出所有的同位角内错角和同旁内角.
图①中∠1和∠3是同位角,
∠2和∠4 是同位角;
∠2和∠3是同旁内角;
图中没有内错角。
图②中∠1和∠5是同位角;
∠4和∠5是内错角;
∠2和∠5 是同旁内角。
2. 填空:如图,在已标出的五个角中,
(1) 直线AC,BD被直线ED所截,∠1与_____是同位角;
(2) ∠1与∠4是直线_____,
_____被直线_____所截得的
内错角;
∠2
ED
AB
AC
(3) ∠2与_____是直线AB,______被直线_____所截得的同旁内角.
∠3
CD
BD
拓展与延伸
3.如图,直线DE过点A,∠B与哪个角是内错角,与哪个角是同旁内角 ∠C与哪个角是内错角,与哪个角是同旁内角 它们分别是哪两条直线被哪一条直线截得的
∠B和∠DAB是直线DE和BC被AB所截而成的内错角;
∠B和∠CAB是直线AC、BC被直线AB所截而成的同旁内角;
∠B和∠BAE是直线DE和BC被直线AB所截而成的同旁内角;
∠C和∠EAC是直线DE和BC被直线AC所截而成的内错角;
∠C和∠BAC是直线AB、BC被直线AC所截而成的同旁内角;
∠C和∠DAC是直线DE、BC被直线AC所截而成的同旁内角.
探索与创新
4.如图,直线a,b被直线c所截,如果有一对同位角相等 (如∠1= ∠5).
∵ ∠1 = ∠5,
∴ a ∥b.
(1) 你能说明其他几对同位角也分别相等吗
∵ a ∥ b,
∴ ∠2 = ∠6, ∠3 = ∠7,
∠4 = ∠8
(两直线平行,同位角相等);
(2)各对内错角是否分别相等 为什么
∵ a ∥ b,
∴ ∠3 = ∠5, ∠4 = ∠6,
(两直线平行,内错角相等);
(3) 此时,两对同旁内角之间具有怎样的数量关系 为什么
∵ a ∥ b,
∴ ∠3+∠6=180°,
∠4 +∠5=180°,
(两直线平行,同旁内角互补);
(4) 如果将上面的“有一对同位角相等”的条件换成“有一对同旁内角互补”,你能得到哪些结论
将上面的“有一对同位角相等”的条件换成“有一对同旁内角互补”,都可以得到 a∥b . 仍然得到(1)(2)(3)的结论.
本课结束!
第 9 章 平行线
青岛版 七年级下册
9 . 1
同位角、内错角、同旁内角
观察与思考
图9-1是小亮所在学校周边的道路示意图,如果把图中的道路都看做直线就得到图9-2.
(1) 在图9-2中,直线AB,CD被直线EF所截,一共形成哪几个角
∠1, ∠2,∠3,∠4, ∠5,∠6,∠7, ∠8,共8个角.
(2) 观察∠1与∠5,它们有怎样的位置关系
∠1与∠5分别在直线AB与CD的同侧,并且都在直线EF的同旁,
具有这种位置关系的一对角叫做同位角.
同样地,∠2与∠6也是同位角,除此之外,图 9-2中还有其他的同位角吗 如果有,请你指出来.
∠3与∠7,
∠4与∠8
(3) 观察∠3与∠5,它们有怎样的位置关系
∠3与∠5都在直线AB,CD之间,并且分别在直线EF的两旁,
具有这种位置关系的一对角叫做内错角.
除∠3与∠5之外,图9-2中还有其他的内错角吗
∠4与∠6,
(4) 观察∠4与∠5,它们有怎样的位置关系
∠4与∠5都在直线AB,CD之间,并且都在直线 EF的同旁,
具有这种位置关系的一对角叫做同旁内角 .
除∠4与∠5之外,图9-2中还有其他的同旁内角吗
∠3与∠6,
在右图中,直线EF,GH被直线AB所截,哪几对角是同位角 哪几对角是内错角 哪几对角是同旁内角
例 1
解:∠ACF与∠ADH,∠FCB与
∠HDB,∠ACE与∠ADG,
∠ECB与∠GDB分别是同位角;
∠FCB与∠ADG, ∠ECB与∠ADH分别是内错角;
∠FCB与∠ADH, ∠ECB与∠ADG分别是同旁内角
例 2
在右图中,直线a,b被直线l所截.
(1) ∠3与哪个角是同位角
∠3与∠7是同位角.
(2) 如果∠1=∠5,那么∠7和∠8分别与∠1有什么数量关系 说明理由.
∠7与∠1相等.
理由是:
∵∠1 = ∠5,而∠7与∠5是对顶角,∠7=∠5,
∴∠7 = ∠1.
(2) 如果∠1=∠5,那么∠7和∠8分别与∠1有什么数量关系 说明理由.
∠8与∠1互补.
理由是:
∵∠1 =∠5,∠8与∠5互补,∴∠8与∠1互补.
随堂练习
1. 如图:∠1与∠2是同位角吗?
是
不是
2. 如图:∠1与∠2是内错角吗?
是
不是
3.如图:∠1与∠2是同旁内角吗?
是
不是
归纳总结
主要内容:两条直线被第三条直线所截而产生的三种角——同位角、内错角、同旁内角.
1.三种角产生的条件及位置特征;
2.判断时应先找到“截线”,再找另外两直线,然后根据角的位置决定是哪一种角.
3.当图形复杂时可把暂时不需要的线段、角等遮住,也可采用图形分解法、图形涂色法以排除干扰.
练 习
1. 如图,直线DE与∠ABC的边BC相交于点P. 视直线AB,DE被直线BC所截, ∠1与∠2,∠1与∠3,∠1与∠4分别是什么角
∠1和∠2是同旁内角
∠1和∠3是内错角
∠1和∠4是同位角
2. 如图,直线AB,CD 被直线 EF所截,在所标出的角中,哪几对角是同位角 哪
几对角是内错角 哪几对角是
同旁内角 类似地,你能讨论
直线 EF,GH被直线AB所截形
成的角的位置关系吗
直线AB、CD被直线EF所截,在所标出的角中∠1和∠3是同位角;
∠1和∠5,∠4和∠2是内错角;
∠2和∠5,∠1和∠4是同旁内角;
直线DF、GH被直线AB所截,在所标出的角中∠2和∠6是同位角;
∠1和∠7是内错角;
∠1和∠6是同旁内角.
习题 9.1
复习与巩固
1.如图①②,直线a,b被直线l所截,在图中已标出的角中,分别找出所有的同位角内错角和同旁内角.
图①中∠1和∠3是同位角,
∠2和∠4 是同位角;
∠2和∠3是同旁内角;
图中没有内错角。
图②中∠1和∠5是同位角;
∠4和∠5是内错角;
∠2和∠5 是同旁内角。
2. 填空:如图,在已标出的五个角中,
(1) 直线AC,BD被直线ED所截,∠1与_____是同位角;
(2) ∠1与∠4是直线_____,
_____被直线_____所截得的
内错角;
∠2
ED
AB
AC
(3) ∠2与_____是直线AB,______被直线_____所截得的同旁内角.
∠3
CD
BD
拓展与延伸
3.如图,直线DE过点A,∠B与哪个角是内错角,与哪个角是同旁内角 ∠C与哪个角是内错角,与哪个角是同旁内角 它们分别是哪两条直线被哪一条直线截得的
∠B和∠DAB是直线DE和BC被AB所截而成的内错角;
∠B和∠CAB是直线AC、BC被直线AB所截而成的同旁内角;
∠B和∠BAE是直线DE和BC被直线AB所截而成的同旁内角;
∠C和∠EAC是直线DE和BC被直线AC所截而成的内错角;
∠C和∠BAC是直线AB、BC被直线AC所截而成的同旁内角;
∠C和∠DAC是直线DE、BC被直线AC所截而成的同旁内角.
探索与创新
4.如图,直线a,b被直线c所截,如果有一对同位角相等 (如∠1= ∠5).
∵ ∠1 = ∠5,
∴ a ∥b.
(1) 你能说明其他几对同位角也分别相等吗
∵ a ∥ b,
∴ ∠2 = ∠6, ∠3 = ∠7,
∠4 = ∠8
(两直线平行,同位角相等);
(2)各对内错角是否分别相等 为什么
∵ a ∥ b,
∴ ∠3 = ∠5, ∠4 = ∠6,
(两直线平行,内错角相等);
(3) 此时,两对同旁内角之间具有怎样的数量关系 为什么
∵ a ∥ b,
∴ ∠3+∠6=180°,
∠4 +∠5=180°,
(两直线平行,同旁内角互补);
(4) 如果将上面的“有一对同位角相等”的条件换成“有一对同旁内角互补”,你能得到哪些结论
将上面的“有一对同位角相等”的条件换成“有一对同旁内角互补”,都可以得到 a∥b . 仍然得到(1)(2)(3)的结论.
本课结束!
同课章节目录
- 第8章 角
- 8.1 角的表示
- 8.2 角的比较
- 8.3 角的度量
- 8.4 对顶角
- 8.5 垂直
- 第9章 平行线
- 9.1 同位角、内错角、同旁内角
- 9.2 平行线和它的画法
- 9.3 平行线的性质
- 9.4 平行线的判定
- 第10章 一次方程组
- 10.1 认识二元一次方程组
- 10.2 二元一次方程组的解法
- 10.3 三元一次方程组
- 10.4 列方程组解应用题
- 第11章 整式的乘除
- 11.1 同底数幂的乘法
- 11.2 积的乘方与幂的乘方
- 11.3 单项式的乘法
- 11.4 多项式乘多项式
- 11.5 同底数幂的除法
- 11.6 零指数幂与负整数指数幂
- 第12章 乘法公式与因式分解
- 12.1 平方差公式
- 12.2 完全平方公式
- 12.3 用提公因式法进行因式分解
- 12.4 用公式法进行因式分解
- 第13章 平面图形的认识
- 13.1 三角形
- 13.2 多边形
- 13.3 圆
- 第14章 位置与坐标
- 14.1 用有序数对表示位置
- 14.2 平面直角坐标系
- 14.3 直角坐标系中的图形
- 14.4 用方向和距离描述两个物体的相对位置
