2014快乐暑假初三升初四衔接复习部分——反比例函数(附答案)
文档属性
| 名称 | 2014快乐暑假初三升初四衔接复习部分——反比例函数(附答案) |  | |
| 格式 | zip | ||
| 文件大小 | 220.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-07-18 12:15:15 | ||
图片预览

文档简介
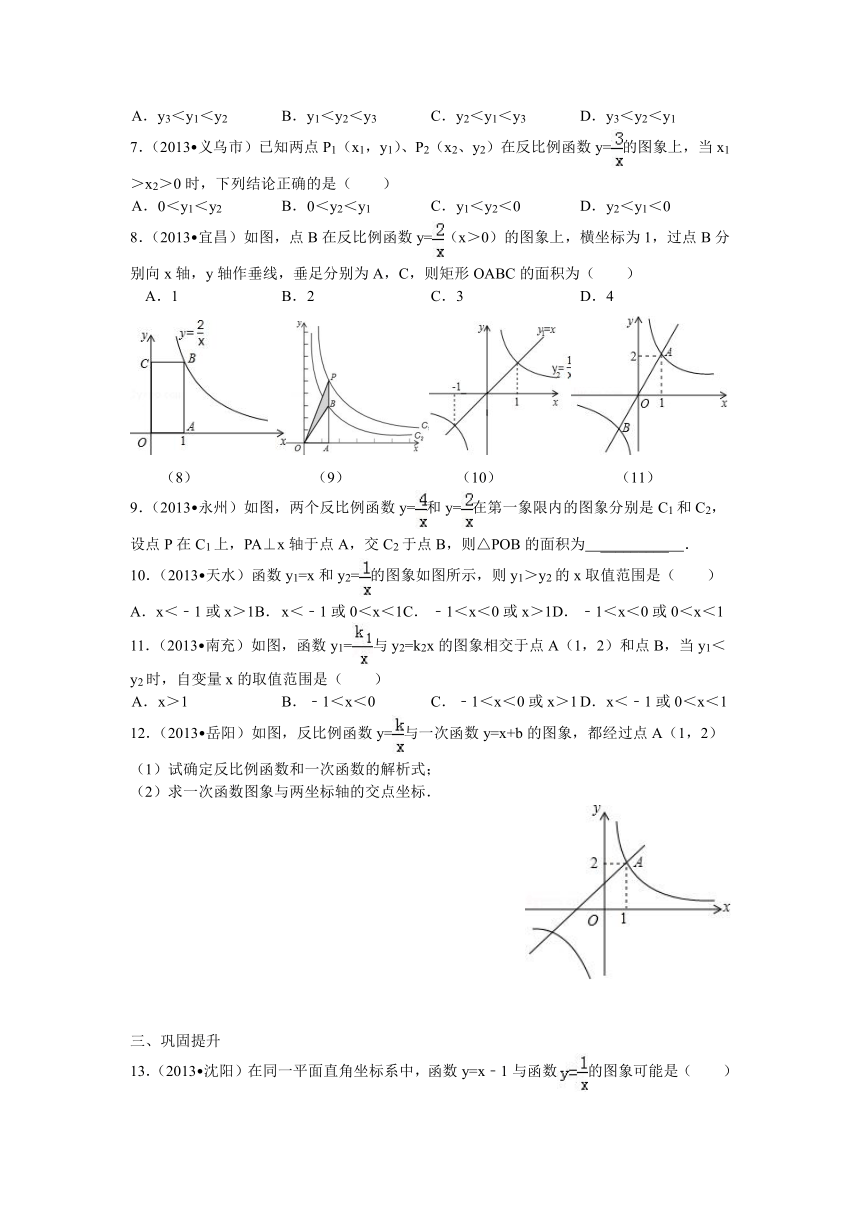
2014快乐暑假初三升初四衔接复习部分——反比例函数(附答案)
一、知识回顾
1、一般的,如果两个变量之间的关系可以表示成 的形式,那么就称作y是x的反比例函数。
2、比例的性质:反比例函数()的图像是 。
当 0时两支曲线分别位于第 ( http: / / www.21cnjy.com ) 象限内,在每一象限内y的值随x的 ;当 0时两支曲线分别位于第 象限内,在每一象限内y的值随x的 ;
3、k的几何意义是 。
二、典例精析
1.(2013 安顺)若是反比例函数,则a的取值为( )
A. 1 B. ﹣l C. ±l D. 任意实数
2.(2012 兰州)近视眼镜的度数y(度 ( http: / / www.21cnjy.com ))与镜片焦距x(m)成反比例,已知400度近视眼镜镜片的焦距为0.25m,则y与x的函数关系式为( )
A. B. C. D. y=
3.(2011 铜仁地区)反比例函数y= (k<0)的大致图象是( )
A.B.C.D.
4.(2013 云南)若ab>0,则一次函数y=ax+b与反比例函数y=在同一坐标系数中的大致图象是( )
A. ( http: / / www.21cnjy.com )B. ( http: / / www.21cnjy.com )C. ( http: / / www.21cnjy.com )D. ( http: / / www.21cnjy.com )
5.(2013 随州)正比例函数y=kx和反比例函数y=﹣(k是常数且k≠0)在同一平面直角坐标系中的图象可能是( )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
6.(2013 株洲)已知点A(1,y1)、B(2,y2)、C(﹣3,y3)都在反比例函数的图象上,则y1、y2、y3的大小关系是( )
A. y3<y1<y2 B. y1<y2<y3 C. y2<y1<y3 D. y3<y2<y1
7.(2013 义乌市)已知两点P1(x1,y1)、P2(x2、y2)在反比例函数y=的图象上,当x1>x2>0时,下列结论正确的是( )
A. 0<y1<y2 B. 0<y2<y1 C. y1<y2<0 D. y2<y1<0
8.(2013 宜昌)如图,点B在反比例函数y=(x>0)的图象上,横坐标为1,过点B分别向x轴,y轴作垂线,垂足分别为A,C,则矩形OABC的面积为( )
A.1 B. 2 C. 3 D. 4
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(8) (9) (10) (11)
9.(2013 永州)如图,两个反比例函数y=和y=在第一象限内的图象分别是C1和C2,设点P在C1上,PA⊥x轴于点A,交C2于点B,则△POB的面积为 _________ .
10.(2013 天水)函数y1=x和y2=的图象如图所示,则y1>y2的x取值范围是( )
A.x<﹣1或x>1B. x<﹣1或0<x<1C. ﹣1<x<0或x>1D. ﹣1<x<0或0<x<1
11.(2013 南充)如图,函数y1=与y2=k2x的图象相交于点A(1,2)和点B,当y1<y2时,自变量x的取值范围是( )
A. x>1 B. ﹣1<x<0 C. ﹣1<x<0或x>1 D. x<﹣1或0<x<1
12.(2013 岳阳)如图,反比例函数y=与一次函数y=x+b的图象,都经过点A(1,2)
(1)试确定反比例函数和一次函数的解析式;
(2)求一次函数图象与两坐标轴的交点坐标.
( http: / / www.21cnjy.com )
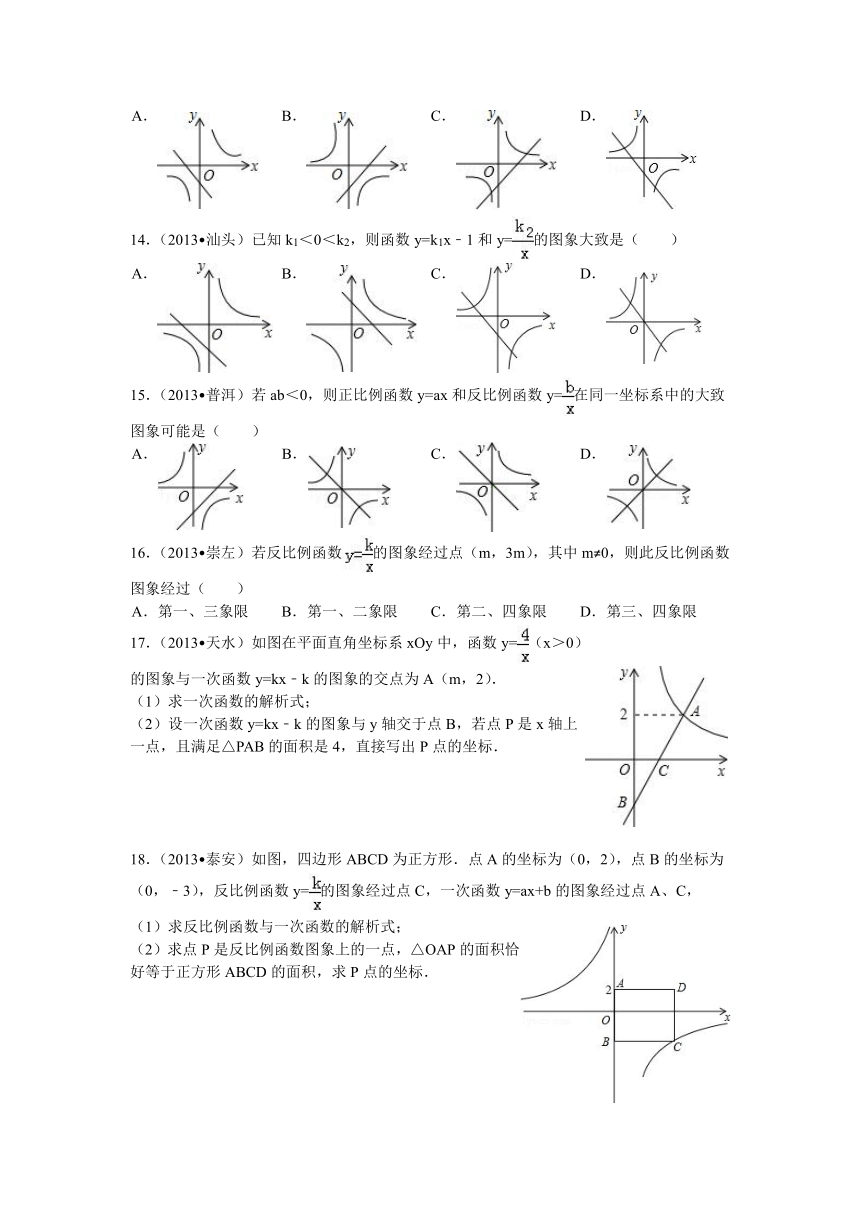
三、巩固提升
13.(2013 沈阳)在同一平面直角坐标系中,函数y=x﹣1与函数的图象可能是( )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
14.(2013 汕头)已知k1<0<k2,则函数y=k1x﹣1和y=的图象大致是( )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
15.(2013 普洱)若ab<0,则正比例函数y=ax和反比例函数y=在同一坐标系中的大致图象可能是( )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
16.(2013 崇左)若反比例函数的图象经过点(m,3m),其中m≠0,则此反比例函数图象经过( )
A. 第一、三象限 B. 第一、二象限 C. 第二、四象限 D. 第三、四象限
17.(2013 天水)如图在平面直角坐标系xOy中,函数y=(x>0)的图象与一次函数y=kx﹣k的图象的交点为A(m,2).
(1)求一次函数的解析式;
(2)设一次函数y=kx﹣k的图象与y轴交于点B,若点P是x轴上一点,且满足△PAB的面积是4,直接写出P点的坐标.
18.(2013 泰安)如图,四边形ABCD为正方形.点A的坐标为(0,2),点B的坐标为(0,﹣3),反比例函数y=的图象经过点C,一次函数y=ax+b的图象经过点A、C,
(1)求反比例函数与一次函数的解析式;
(2)求点P是反比例函数图象上的一点,△OAP的面积恰好等于正方形ABCD的面积,求P点的坐标.
四、深化提高
19.(2013 淄博)如图,矩形AOBC的面积为4,反比例函数的图象的一支经过矩形对角线的交点P,则该反比例函数的解析式是( )
A. B. C. D.
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(19) (20) (22)
20.(2013 内江)如图,反比例函数(x>0)的图象经过矩形OABC对角线的交点M,分别于AB、BC交于点D、E,若四边形ODBE的面积为9,则k的值为( )
A. 1 B. 2 C. 3 D. 4
21.(2013 六盘水)下列图形中,阴影部分面积最大的是( )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
22.(2012 漳州)如图,点A(3,n)在双曲线y=上,过点A作AC⊥x轴,垂足为C.线段OA的垂直平分线交OC于点M,则△AMC周长的值是 _________ .
23.(2012 泰安)如图,一次函数y=kx+b的图象与坐标轴分别交于A,B两点,与反比例函数y=的图象在第二象限的交点为C,CD⊥x轴,垂足为D,若OB=2,OD=4,△AOB的面积为1.
(1)求一次函数与反比例的解析式;
(2)直接写出当x<0时,kx+b﹣>0的解集.
( http: / / www.21cnjy.com )
五、课时检测
24.(2013 滨州)若点A(1,y1)、B(2,y2)都在反比例函数的图象上,则y1、y2的大小关系为( )
A. y1<y2 B. y1≤y2 C. y1>y2 D. y1≥y2
25.(2012 宜宾)如图,一次函数y1=ax+b(a≠0)与反比例函数的图象交于A(1,4)、B(4,1)两点,若使y1>y2,则x的取值范围是 _________ .
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(25) (26) (27)
26.(2012 连云港)如图,直线y=k1x+b与双曲线y=交于A、B两点,其横坐标分别为1和5,则不等式k1x<+b的解集是 _________ .
27.(2012 甘孜州)如图,点A在双曲线上,点B在双曲线上,C,D在x轴上,若四边形ABCD为矩形,则它的面积为 _________ .
28.(2013 红河州)如图,正比例函数y1=x的图象与反比例函数(k≠0)的图象相交于A、B两点,点A的纵坐标为2.
(1)求反比例函数的解析式;
(2)求出点B的坐标,并根据函数图象,写出当y1>y2时,自变量x的取值范围.
( http: / / www.21cnjy.com )
2014快乐暑假初三升初四衔接复习部分——反比例函数参考答案
1.A. 2.C.3.D.4.A.5.C.6.D.7.A.8.B.9. 1 10.C 11.C.
12.解:(1)∵反比例函数y=与一次函数y=x+b的图象,都经过点A(1,2),
∴将x=1,y=2代入反比例解析式得:k=1×2=2,
将x=1,y=2代入一次函数解析式得:b=2﹣1=1,
∴反比例函数的解析式为y=,一次函数的解析式为y=x+1;
(2)对于一次函数y=x+1,
令y=0,可得x=﹣1;令x=0,可得y=1.
∴一次函数图象与x轴,y轴的交点坐标分别为(﹣1,0),(0,1).
13.C.14.A.15.C.16.A
17.解:(1)将A(m,2)代入y=(x>0)得,m=2,则A点坐标为A(2,2),
将A(2,2)代入y=kx﹣k得,2k﹣k=2,解得k=2,则一次函数解析式为y=2x﹣2;
(2)∵一次函数y=2x﹣2与x轴的交点为C(1,0),与y轴的交点为(0,﹣2),
S△ABP=S△ACP+S△BPC,∴×2CP+×2CP=4,解得CP=2,
则P点坐标为(3,0),(﹣1,0).
( http: / / www.21cnjy.com )
18.解:(1)∵点A的坐标为(0,2),点B的坐标为(0,﹣3),∴AB=5,
∵四边形ABCD为正方形,∴点C的坐标为(5,﹣3).
∵反比例函数y=的图象经过点C,∴﹣3=,解得k=﹣15,
∴反比例函数的解析式为y=﹣;
∵一次函数y=ax+b的图象经过点A,C,∴,解得,
∴一次函数的解析式为y=﹣x+2;
(2)设P点的坐标为(x,y).
∵△OAP的面积恰好等于正方形ABCD的面积,∴×OA |x|=52,∴×2 |x|=25,
解得x=±25.
当x=25时,y=﹣=﹣;
当x=﹣25时,y=﹣=.∴P点的坐标为(25,﹣)或(﹣25,).
19. C.
解:作PE⊥x轴,PF⊥y轴,如图,∵点P为矩形AOBC对角线的交点,
∴矩形OEPF的面积=矩形AOBC的面积=×4=1,∴|k|=1,而k>0,∴k=1,
∴过P点的反比例函数的解析式为y=.
20.C.
解:由题意得:E、M、D位于反比例函数图象上,则S△OCE=,S△OAD=,
过点M作MG⊥y轴于点G,作MN⊥x轴于点N,则S□ONMG=|k|,
又∵M为矩形ABCO对角线的交点,
∴S矩形ABCO=4S□ONMG=4|k|,
由于函数图象在第一象限,k>0,则++9=4k, 解得:k=3.
21.C.22. 4
23.解:(1)∵OB=2,△AOB的面积为1.∴B(﹣2,0),OA=1,∴A(0,﹣1)
∴∴∴y=﹣x﹣1
又∵OD=4,CD⊥x轴,∴C(﹣4,y),
将x=﹣4代入y=﹣x﹣1得y=1,∴C(﹣4,1)
∴1=,∴m=﹣4,∴y=﹣,∴反比例函数的解析式为:y=﹣;
(2)当x<0时,kx+b﹣>0的解集是x<﹣4.
24.C.25.x<0或1<x<4 .26. ﹣5<x<﹣1或x>0 .27. 2
28.解:(1)设A点的坐标为(m,2),代入y1=x得:m=2,
∴点A的坐标为(2,2),∴k=2×2=4,∴反比例函数的解析式为y2=;
(2)当y1=y2时,x=,解得:x=±2,∴点B的坐标为(﹣2,﹣2),
则由图象可知,当y1>y2时,自变量x的取值范围是:﹣2<x<0或x>2.
一、知识回顾
1、一般的,如果两个变量之间的关系可以表示成 的形式,那么就称作y是x的反比例函数。
2、比例的性质:反比例函数()的图像是 。
当 0时两支曲线分别位于第 ( http: / / www.21cnjy.com ) 象限内,在每一象限内y的值随x的 ;当 0时两支曲线分别位于第 象限内,在每一象限内y的值随x的 ;
3、k的几何意义是 。
二、典例精析
1.(2013 安顺)若是反比例函数,则a的取值为( )
A. 1 B. ﹣l C. ±l D. 任意实数
2.(2012 兰州)近视眼镜的度数y(度 ( http: / / www.21cnjy.com ))与镜片焦距x(m)成反比例,已知400度近视眼镜镜片的焦距为0.25m,则y与x的函数关系式为( )
A. B. C. D. y=
3.(2011 铜仁地区)反比例函数y= (k<0)的大致图象是( )
A.B.C.D.
4.(2013 云南)若ab>0,则一次函数y=ax+b与反比例函数y=在同一坐标系数中的大致图象是( )
A. ( http: / / www.21cnjy.com )B. ( http: / / www.21cnjy.com )C. ( http: / / www.21cnjy.com )D. ( http: / / www.21cnjy.com )
5.(2013 随州)正比例函数y=kx和反比例函数y=﹣(k是常数且k≠0)在同一平面直角坐标系中的图象可能是( )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
6.(2013 株洲)已知点A(1,y1)、B(2,y2)、C(﹣3,y3)都在反比例函数的图象上,则y1、y2、y3的大小关系是( )
A. y3<y1<y2 B. y1<y2<y3 C. y2<y1<y3 D. y3<y2<y1
7.(2013 义乌市)已知两点P1(x1,y1)、P2(x2、y2)在反比例函数y=的图象上,当x1>x2>0时,下列结论正确的是( )
A. 0<y1<y2 B. 0<y2<y1 C. y1<y2<0 D. y2<y1<0
8.(2013 宜昌)如图,点B在反比例函数y=(x>0)的图象上,横坐标为1,过点B分别向x轴,y轴作垂线,垂足分别为A,C,则矩形OABC的面积为( )
A.1 B. 2 C. 3 D. 4
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(8) (9) (10) (11)
9.(2013 永州)如图,两个反比例函数y=和y=在第一象限内的图象分别是C1和C2,设点P在C1上,PA⊥x轴于点A,交C2于点B,则△POB的面积为 _________ .
10.(2013 天水)函数y1=x和y2=的图象如图所示,则y1>y2的x取值范围是( )
A.x<﹣1或x>1B. x<﹣1或0<x<1C. ﹣1<x<0或x>1D. ﹣1<x<0或0<x<1
11.(2013 南充)如图,函数y1=与y2=k2x的图象相交于点A(1,2)和点B,当y1<y2时,自变量x的取值范围是( )
A. x>1 B. ﹣1<x<0 C. ﹣1<x<0或x>1 D. x<﹣1或0<x<1
12.(2013 岳阳)如图,反比例函数y=与一次函数y=x+b的图象,都经过点A(1,2)
(1)试确定反比例函数和一次函数的解析式;
(2)求一次函数图象与两坐标轴的交点坐标.
( http: / / www.21cnjy.com )
三、巩固提升
13.(2013 沈阳)在同一平面直角坐标系中,函数y=x﹣1与函数的图象可能是( )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
14.(2013 汕头)已知k1<0<k2,则函数y=k1x﹣1和y=的图象大致是( )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
15.(2013 普洱)若ab<0,则正比例函数y=ax和反比例函数y=在同一坐标系中的大致图象可能是( )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
16.(2013 崇左)若反比例函数的图象经过点(m,3m),其中m≠0,则此反比例函数图象经过( )
A. 第一、三象限 B. 第一、二象限 C. 第二、四象限 D. 第三、四象限
17.(2013 天水)如图在平面直角坐标系xOy中,函数y=(x>0)的图象与一次函数y=kx﹣k的图象的交点为A(m,2).
(1)求一次函数的解析式;
(2)设一次函数y=kx﹣k的图象与y轴交于点B,若点P是x轴上一点,且满足△PAB的面积是4,直接写出P点的坐标.
18.(2013 泰安)如图,四边形ABCD为正方形.点A的坐标为(0,2),点B的坐标为(0,﹣3),反比例函数y=的图象经过点C,一次函数y=ax+b的图象经过点A、C,
(1)求反比例函数与一次函数的解析式;
(2)求点P是反比例函数图象上的一点,△OAP的面积恰好等于正方形ABCD的面积,求P点的坐标.
四、深化提高
19.(2013 淄博)如图,矩形AOBC的面积为4,反比例函数的图象的一支经过矩形对角线的交点P,则该反比例函数的解析式是( )
A. B. C. D.
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(19) (20) (22)
20.(2013 内江)如图,反比例函数(x>0)的图象经过矩形OABC对角线的交点M,分别于AB、BC交于点D、E,若四边形ODBE的面积为9,则k的值为( )
A. 1 B. 2 C. 3 D. 4
21.(2013 六盘水)下列图形中,阴影部分面积最大的是( )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
22.(2012 漳州)如图,点A(3,n)在双曲线y=上,过点A作AC⊥x轴,垂足为C.线段OA的垂直平分线交OC于点M,则△AMC周长的值是 _________ .
23.(2012 泰安)如图,一次函数y=kx+b的图象与坐标轴分别交于A,B两点,与反比例函数y=的图象在第二象限的交点为C,CD⊥x轴,垂足为D,若OB=2,OD=4,△AOB的面积为1.
(1)求一次函数与反比例的解析式;
(2)直接写出当x<0时,kx+b﹣>0的解集.
( http: / / www.21cnjy.com )
五、课时检测
24.(2013 滨州)若点A(1,y1)、B(2,y2)都在反比例函数的图象上,则y1、y2的大小关系为( )
A. y1<y2 B. y1≤y2 C. y1>y2 D. y1≥y2
25.(2012 宜宾)如图,一次函数y1=ax+b(a≠0)与反比例函数的图象交于A(1,4)、B(4,1)两点,若使y1>y2,则x的取值范围是 _________ .
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(25) (26) (27)
26.(2012 连云港)如图,直线y=k1x+b与双曲线y=交于A、B两点,其横坐标分别为1和5,则不等式k1x<+b的解集是 _________ .
27.(2012 甘孜州)如图,点A在双曲线上,点B在双曲线上,C,D在x轴上,若四边形ABCD为矩形,则它的面积为 _________ .
28.(2013 红河州)如图,正比例函数y1=x的图象与反比例函数(k≠0)的图象相交于A、B两点,点A的纵坐标为2.
(1)求反比例函数的解析式;
(2)求出点B的坐标,并根据函数图象,写出当y1>y2时,自变量x的取值范围.
( http: / / www.21cnjy.com )
2014快乐暑假初三升初四衔接复习部分——反比例函数参考答案
1.A. 2.C.3.D.4.A.5.C.6.D.7.A.8.B.9. 1 10.C 11.C.
12.解:(1)∵反比例函数y=与一次函数y=x+b的图象,都经过点A(1,2),
∴将x=1,y=2代入反比例解析式得:k=1×2=2,
将x=1,y=2代入一次函数解析式得:b=2﹣1=1,
∴反比例函数的解析式为y=,一次函数的解析式为y=x+1;
(2)对于一次函数y=x+1,
令y=0,可得x=﹣1;令x=0,可得y=1.
∴一次函数图象与x轴,y轴的交点坐标分别为(﹣1,0),(0,1).
13.C.14.A.15.C.16.A
17.解:(1)将A(m,2)代入y=(x>0)得,m=2,则A点坐标为A(2,2),
将A(2,2)代入y=kx﹣k得,2k﹣k=2,解得k=2,则一次函数解析式为y=2x﹣2;
(2)∵一次函数y=2x﹣2与x轴的交点为C(1,0),与y轴的交点为(0,﹣2),
S△ABP=S△ACP+S△BPC,∴×2CP+×2CP=4,解得CP=2,
则P点坐标为(3,0),(﹣1,0).
( http: / / www.21cnjy.com )
18.解:(1)∵点A的坐标为(0,2),点B的坐标为(0,﹣3),∴AB=5,
∵四边形ABCD为正方形,∴点C的坐标为(5,﹣3).
∵反比例函数y=的图象经过点C,∴﹣3=,解得k=﹣15,
∴反比例函数的解析式为y=﹣;
∵一次函数y=ax+b的图象经过点A,C,∴,解得,
∴一次函数的解析式为y=﹣x+2;
(2)设P点的坐标为(x,y).
∵△OAP的面积恰好等于正方形ABCD的面积,∴×OA |x|=52,∴×2 |x|=25,
解得x=±25.
当x=25时,y=﹣=﹣;
当x=﹣25时,y=﹣=.∴P点的坐标为(25,﹣)或(﹣25,).
19. C.
解:作PE⊥x轴,PF⊥y轴,如图,∵点P为矩形AOBC对角线的交点,
∴矩形OEPF的面积=矩形AOBC的面积=×4=1,∴|k|=1,而k>0,∴k=1,
∴过P点的反比例函数的解析式为y=.
20.C.
解:由题意得:E、M、D位于反比例函数图象上,则S△OCE=,S△OAD=,
过点M作MG⊥y轴于点G,作MN⊥x轴于点N,则S□ONMG=|k|,
又∵M为矩形ABCO对角线的交点,
∴S矩形ABCO=4S□ONMG=4|k|,
由于函数图象在第一象限,k>0,则++9=4k, 解得:k=3.
21.C.22. 4
23.解:(1)∵OB=2,△AOB的面积为1.∴B(﹣2,0),OA=1,∴A(0,﹣1)
∴∴∴y=﹣x﹣1
又∵OD=4,CD⊥x轴,∴C(﹣4,y),
将x=﹣4代入y=﹣x﹣1得y=1,∴C(﹣4,1)
∴1=,∴m=﹣4,∴y=﹣,∴反比例函数的解析式为:y=﹣;
(2)当x<0时,kx+b﹣>0的解集是x<﹣4.
24.C.25.x<0或1<x<4 .26. ﹣5<x<﹣1或x>0 .27. 2
28.解:(1)设A点的坐标为(m,2),代入y1=x得:m=2,
∴点A的坐标为(2,2),∴k=2×2=4,∴反比例函数的解析式为y2=;
(2)当y1=y2时,x=,解得:x=±2,∴点B的坐标为(﹣2,﹣2),
则由图象可知,当y1>y2时,自变量x的取值范围是:﹣2<x<0或x>2.
