初中数学青岛版七年级下册10.4 列方程组解应用题课件(共80张PPT)
文档属性
| 名称 | 初中数学青岛版七年级下册10.4 列方程组解应用题课件(共80张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 61.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-11 19:17:15 | ||
图片预览











文档简介
(共80张PPT)
第10章 一次方程组
青岛版 七年级下册
10 . 4
列方程组解应用题
知识回顾
列一元一次方程解应用题的步骤:
审、列、解、验、答.
交流与发现
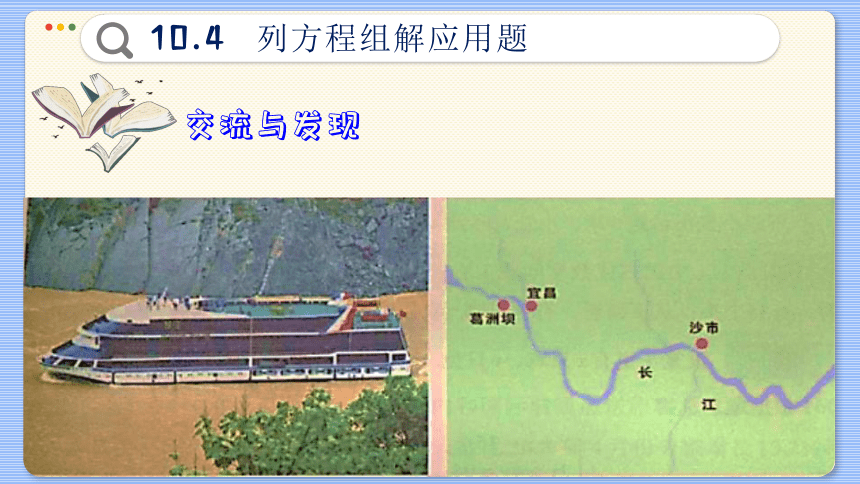
长江上一艘游船从沙市港出发,船速为17 千米/时,经过若干小时到达宜昌港.如果船速增加1千米/时,那么用同样多的时间,游船可到达宜昌上游9千米处的葛洲坝.提速前游船由沙市港航行到宜昌港所用的时间是多少 沙市港到宜昌港的航程是多少
在这个问题中,
(1) 已知量是什么 未知量是什么
(2) 等量关系是什么
速度×时间=路程
(3) 如果设游船航行所用的时间为x时,沙市港到宜昌港的航程为y千米你能根据问题中的两个等量关系列出方程组吗
17x = y
(17+1)x = y+9
(4) 你会解所列的方程组吗
17x = y
18x = y+9
进一步整理为:
17x = y
(17+1)x = y+9
例 1
小亮和小莹练习赛跑.如果小亮让小莹先跑 10米,那么小亮跑5秒就追上小莹;如果小亮让小莹先跑 2 秒,那么小亮跑 4秒就追上小莹. 两人每秒各跑多少米
等量关系是:
(1)小亮跑5秒的路程=小莹跑5秒的路程+10米;
(2)小亮跑4秒的路程=小莹跑 (4+2)秒的路程.
解:设小亮每秒跑x米,小莹每秒跑y米.
根据题意,得
5x = 5y +10,
4x = (4+2) y
解得
x = 6,
y= 4.
经检验,方程组的解符合题意.
所以小亮每秒跑6米,小莹每秒跑4米.
例 2
(中国古代数学问题) 有若干只鸡和兔放在同一个笼子里.从上面看,有35个头;从下面看,有94只脚.问笼子里有几只鸡 几只兔
解:设笼子里有x只鸡、y只兔.
已知共有35个头、94只脚.
根据题意,得
x +y = 35 ,
2x +4y = 94.
解得
x = 23,
y= 12.
经检验,方程组的解符合题意.
所以,笼子里有23只鸡、12只兔.
对于这个问题,你能用四则运算的方法和列一元一次方程的方法求解吗 比较这两种方法与列二元一次方程组的方法,你认为它们各有什么特点 与同学交流.
挑战自我
甲、乙二人正在谈论他们的年龄.
甲:在我是你今年的岁数时,你那年10岁.
乙:在我是你今年的岁数时,你那年25岁.
想一想,甲、乙二人谁的年龄大 今年甲、乙二人各多少岁
练 习
1. 为绿化校园,时代中学买了杨树苗和柳树苗共 100棵.杨树苗每棵3 元,柳树苗每棵7元,买树苗共用460 元.两种树苗各买了多少棵
解:设买杨树苗x棵,买柳树苗y棵,
根据题意,得
x +y = 100 ,
3x +7y = 460.
解得
x = 60,
y= 40.
答:买杨树苗60棵,买柳树苗40棵.
2. 如图,用8块相同的长方形瓷砖拼成一个宽为60厘米的长方形灶台面.求每块瓷砖的长和宽 (瓷砖间的缝隙忽略不计 ).
解:设小长方形瓷砖的长为x厘米,宽为y厘米.
根据题意,得
x +y = 60 ,
x =3y.
解得
x = 45,
y= 15.
答:每块瓷砖的长为45厘米,宽为15厘米.
例 3
2010年4月份中国民航国内和国际航线运送旅客总人数共 2 160万人,其中,国内和国际航线运送旅客人数比2009 年4月份分别增长 13.2%和28.8%,2009年4月份国内航线和国际航线运送旅客总人数为1894万人,那么2009 年4月份国内和国际航线运送旅客分别有多少万人(结果精确到万人)
设2009年4月份中国民航国内航线运送旅客x万人,国际航线运送旅客y万人,得到下表:
2009年4月份 2010年4月份
国内航线运送人数/万人 x (1+13.2%)x
国际航线运送人数/万人 y (1+28.8%)y
合计/万人 1894 2160
解:设2009年4月份中国民航国内航线运送旅客x万人,国际航线运送旅客y万人.
根据题意,得
x +y = 1894 ,
(1+13.2%)x+(1+28.8% )y= 2160.
解这个方程组,得
x ≈1791,
y ≈103.
经检验,方程组的解符合题意.
所以2009年4月份中国民航国内航线运送旅客1791万人,国际航线运送旅客103万人
加油站
在解决一类实际问题时,可以通过列出方程组表示问题中的全部数量关系,所以方程组也是刻画现实世界数量关系的有效模型.
例 4
果园要将一批水果运往某地,打算租用某汽车运输公司的甲、乙两种货车.过去两次租用这两种货车的信息如下表所示:
第一次 第二次
甲种货车车辆数 /辆 2 5
乙种货车车辆数 /辆 3 6
累计运货量/吨 15.5 35
现打算租用该公司 3 辆甲种货车和 5 辆种货车,可一次刚好运完这批水果.如果每吨运费为30元,果园应付运费多少元
等量关系是:
(1) 2辆甲种货车运量+3辆乙种货车运量=15.5吨;
(2) 5辆甲种货车运量+6辆乙种货车运量=35吨
根据题意,得
2x + 3y = 15.5 ,
5x + 6y = 35.
解得
x =4,
y =2.5.
经检验,方程组的解符合题意.
这次运水果所需运费为30×(4×3+2.5×5) =735(元)
所以,果园应付运费735元
智趣园
两鼠穿墙
《九章算术》提出了一个有趣的问题:“今有垣厚五尺,两鼠对穿,大鼠日一尺,小鼠也日一尺.大鼠日自倍,小鼠日自半,问何日相逢,各穿几何 ”
意思是说:今有一道墙,厚5尺,两只老鼠从墙的两边分别打洞穿墙.大老鼠第一天进一尺,以后每天的进度是前一天的2倍;小老鼠第一天也进1尺,以后每天的进度是前一天的一半.问几天后两鼠相遇;此时.两鼠各穿墙几尺
该题当初是用“盈不足术”求解的.学过一次方程组后,我们也可以用二元一次方程组求解.由题意可知,穿墙第一天,大鼠、小鼠各穿墙1尺,共2尺;穿墙第二天,大鼠穿墙2尺,小鼠穿墙尺.两天大鼠和小鼠共穿墙尺,离穿透墙尚差尺.到第三天时,不用1天二鼠即可相遇.
在穿墙的第三天,设大鼠前进了x尺,小鼠前进了y尺,大鼠该天穿墙速度为4尺/天,小鼠为尺/天.等量关系是:①大鼠、小鼠一共穿墙尺;②该天在相遇前大、小鼠用的时间相等.
你能根据以上分析列出二元一次方程组来求解吗
练 习
1. 时代中学师生 100 人到甲、乙两公司参加社会实践活动,到甲公司的人数比到乙公司的人数的2倍少8 人,到两公司参加社会实践的人数各多少
解:设到乙公司参加社会实践活动的有x人,则到甲公司参加社会实践活动的有(2x-8)人,
根据题意得,(2x-8) +x =100,
解得 x=36
则 2x-8=2×36-8=64.
答:到甲公司参加社会实践活动的有64人,到乙公司参加社会实践活动的有36人.
2. 山青林场有一块面积为 58 公顷的土地,现计划将其中的开辟为果园,其余的土地种粮食和蔬菜,并且种蔬菜的土地面积是种粮食的土地面积的. 该林场计划种蔬菜和粮食各多少公顷
解:设计划种蔬菜x公顷,种粮食y公顷,
根据题意,得
x + 3= 58×(1-) ,
x = y.
解得
x =8.7,
y =34.8.
答:该农场计划种蔬菜8.7公顷,种粮食34.8公顷.
例 5
一个三位数,三位数字之和为 12,个位数字是百位数字与十位数字之和的2倍,百位数字是十位数字的3倍,求这个三位数.
解:设这个三位数的个位数字为x,十位数字为y,百位数字为z.
根据题意,得
x+y+z = 12,
x = 2(y+z)
z = 3y.
解得
x =8,
y =1,
z =3.
经检验,方程组的解符合题意.
所以这个三位数是318.
* 例 6
(中国古代数学问题)今有上等黍3捆,中等黍2捆,下等黍 1捆,共打出黍米39斗;又有上等黍2捆,中等黍3捆,下等黍1捆,共打出黍米34斗;再有上等黍1捆,中等黍2捆,下等黍3捆,共打出黍米26斗.问每捆上、中、下黍各能打出黍米多少斗
解:设每捆上、中、下黍分别能打出黍米x斗、y斗、z斗.
根据题意,得
3x+2y+z = 39,
2x+3y+z= 34,
x+2y+3z= 26.
解得
x =,
y = ,
z = .
经检验,方程组的解符合题意.
所以,每捆上、中、下泰分别能打出黍米斗、 斗、 斗.
挑战自我
小亮、小莹和大刚每人面前各放有一堆栗子.小亮将自己面前的栗子分出一些给另外二人后,这二人的栗子数各增加1倍.接着小莹又将自己面前的栗子分些给小亮和大刚,小亮和大刚的栗子数都增加了1倍.
然后,大刚又分给另外二人一些栗子,使小亮和小莹面前的栗子数也都增加1倍. 这时,他们三人面前的栗子竟然都是 24颗.
你知道他们三人面前原来各有多少颗栗子吗
史海漫游
古老的百鸡问题
公元5世纪左右,北魏时期的数学家张丘建在他所著的《 张丘建算经 》中提出了一个著名的“百鸡问题”;
《张丘建算经》 (宋刻本 )
关于百鸡问题的记载
(选自《中国大百科全书·数学》)
《张丘建算经》 (宋刻本 )
关于百鸡问题的记载
(选自《中国大百科全书·数学》)
“今有鸡翁一,直钱五;鸡母一,直钱三;鸡雏三,直钱一.凡百钱买鸡百只,问鸡翁、母、雏各几何 ”
《张丘建算经》 (宋刻本 )
关于百鸡问题的记载
(选自《中国大百科全书·数学》)
题目大意是:一只公鸡价值 5钱 (我国古代的一种货币单位),一只母鸡价值3 钱,三只维鸡价值 1钱.用100钱买了100只鸡,问买公鸡、母鸡和雏鸡各多少只.
这一问题可利用列方程组的方法解决. 设x,y,z 分别表示所买公鸡、母鸡、雏鸡的只数,根据题意,得
这个方程组中有两个方程,却有三个未知数. 这类方程组在数学上称为不定方程组. 本题是求一个三元一次不定方程组的正整数解问题. 这一问题的提出标志着我国在公元5世纪时已对不定方程组有了系统深入的研究,并为后人学习不定方程组的求解提供了一个入门的范例.
利用我们学过的知识,可以采用下面的方法解这个不定方程组:
由②×3-①,化简得
7x+4y=100 .
y=25-x .
因为y是正整数,所以x应是4的整数倍,且 (25- x) 也是正整数,所以x只能取4,8,12. 由此得
所以,公鸡、母鸡、雏鸡各买了4只、18只、78只;或8只、11只、81只;或12只、4只、84只.
练 习
*1.甲、乙、丙三个数的和是25,甲数的等于乙数的,甲数比乙数与丙数的和少1.求这三个数.
解:设甲数为x,乙数为y,丙数为z.
根据题意,得
x + y + z = 25,
x = y,
y + z - x = 1.
解得
x =12,
y =8,
z =5.
答:甲数为12,乙数为8,丙数为5.
*2. 某市举行中学生足球联赛,比赛的计分规则为:胜一场得3 分,平一场得1分,负一场得0分. 时代中学足球队在12场比赛中,平和负
的场数之和等于胜的场数,共
积21分.这个队在这届联赛中胜、
平、负各几场
解:设这个队在这届联赛中胜、平、负各x场、y场、z场.
根据题意,得
x + y + z = 12,
y +z= ,
3x+y = 21.
解得
x =6,
y =3,
z =3.
答:这个队在这届联赛中胜、平、负各6场、3场、3场.
习题 10.4
复习与巩固
1. (中国古代数学问题)几个合作经营的商人正分配所得银两,某人在隔壁听见他们说,如果每人分得7两,就剩下4两; 如果每人分得9两,还少半斤 (旧时1斤= 16两).你知道共有多少商人和多少银两吗
解:设共有商人x人和银两y两,
根据题意,得
7x +4 = y ,
9x-8= y.
解得
x =6,
y =46.
经检验,方程组的解符合题意.
答:共有商人6人,银两46两.
2.“十一”黄金周期间,某景区共接待省内、外游客122万人,总收入达4.8亿元,其中省内、外游客人均消费分别为160元和1200元.该景区接待省内、外游客各多少万人(精确到1万人)
解:设省内旅游者x万人次,省外旅游者y万人次,
根据题意,得
x +y =122 ,
160x+1200y=4 8000 0000.
解得
x ≈46 ,
y ≈72.
答:该景区接待省内外游客各为46和72万人.
3. 每千克大豆饼和棉籽饼中,磷和钾的含量(单位:克)分别如下表所示:
磷 钾
大豆饼 13.2 21.3
棉籽饼 16.3 9.7
现在要用这两种肥料配制成含磷 45.8 千克、钾40.7 千克的混合肥料.大豆饼和棉籽饼各需多少千克
解:设需要大豆饼x,棉籽饼y.
根据题意,得
13.2x+16.3y =45.8,
21.3x+9.7y=40.7.
解得
x =10,
y =20.
故配置成含磷45.8千克,含40.7千克的混合肥料需要大豆饼10千克棉籽饼20千克.
4. 暑假时一批中学生参加夏令营,途经某旅店住宿.如果每间客房安排住7人,就会有7人没有地方住;如果每间客房安排住9人,就会空出一间房. 求旅店的客房数和中学生的人数.
解:设旅店的客房数为x间,中学生的人数为y人.
根据题意,得
7x+7 = y,
9(x-1)=y.
解得
x =8,
y =63.
答:旅店的客房数为8间,中学生的人数为63人.
5. 某开发区去年的出口创汇额为25 亿美元,今年达到30.55 亿美元.已知今年上半年的出口创汇额比去年同期增长 18%,下半年比去年同期增长 25%,求今年上半年和下半年的出口创汇额.
解:设去年上半年出口创汇额为x亿美元,去年下半年的出口创汇额为y亿美元.
则今年上半年出口创汇额为:
(1+18%) x=1.18x (亿美元),
今年下半年的出口创汇额为:
(1+25%)y=1.25y (亿美元),
根据题意,得
x+y = 25,
1.18z +1.25y=30.55.
解得
x =10,
y =15.
1.18x=11.8亿美元,1.25y=18.75亿美元,
答:今年上半年的出口创汇额11.8亿美元,下半年的出口创汇额18.75亿美元
6. 张大婶和王姐去菜市场买菜. 张大婶买了土豆3千克、菠菜2千克,共花费10.2元;王姐买了芹菜1千克、土豆2千克、菠菜1千克,共花费9.2元. 已知芹菜每千克3元,问土豆和菠菜每千克各多少元.
解:设土豆每千克x元,菠菜每千克y元,
根据题意,得
3x +2y =10.2,
3+2x+y=9.2.
解得
x =2.2,
y =2.
答:故土豆每千克2.2元,菠菜每千克2元.
拓展与延伸
7.一张方桌由一个桌面和四条桌腿组成. 如果1立方米木料可制作桌面 50个,或制作桌腿300条. 现有5立方米木料,请你设计一下,用多少木料做桌面,用多少木料做桌腿,恰好配成方桌多少张
解:设用xm3木料做桌面,则用ym3木料做桌腿,恰好配成方桌,
根据题意,得
4×50x =300y,
x+y=5.
解得
x =3,
y =2.
50×3=150张
∴用3m3木料做桌面,用2m3木料做桌腿,恰好配成方桌150张.
*8. (中国古代问题)买2匹马、3头牛或4只羊,价钱分别都不满10 000文(古时货币单位). 如果买2匹马加上1头牛,或者买3头牛加上1只羊,或者买4只羊加上1匹马,那么各自的价钱正好都是10 000文.求马、牛、羊的单价.
解:设1匹马的价格为x文,1头牛的价格为y文,1只羊的价格为z文.
根据题意,得
2x +y =10000,
3y+z=10000,
4z+x=10000.
解得
x =3600,
y =2800,
z=1600.
答:1匹马的价格为3600文,1头牛的价格为2800文,1只羊的价格为1600文.
*9.某公路收费站对过往车辆的收费标准是:大客车30元,小客车15元,小轿车 10元. 某天通过该收费站的大客车是小客车数量的,小客车是小轿车数量的,收取小轿车的通行费比大客车和小客车通行费之和少1050元.求当天这三种车辆通过的数量.
解:设当天通过该收费站的小轿车有x辆,则当天通过该收费站的小客车有x辆,大客车有 ×x =x辆,
依题意,得: 30×x+15×x-10x = 1050,
解得:x = 231,
∴ x =84, x =70.
答:当天通过该收费站的小轿车有231辆,小客车有84辆,大客车有70辆.
10.《一千零一夜》中有这样一段文字: 有一群鸽子,其中一部分在树上欢歌,另一部分在地上觅食.树上的一只鸽子对地上的鸽子说:“如果从你们中飞上来一只,那么树下的鸽子是整个鸽群的;如果从树上飞下去一只,树上、树下的鸽子就一样多.”你知道原来树上、树下的鸽子各多少只
解:设树上有x只鸽子,树下有y只鸽子.
根据题意,得
y-1 =(x+y),
x+1=y+ 1.
解得
x =7,
y =5.
答:树上原有7只鸽子,树下有5只鸽子。
根据题意,得
2y-x =3,
y=x-2.
探索与创新
11. 甲、乙二人骑自行车同时从相距5千米的两地相向而行,经过 10分钟相遇.
(1) 求甲、乙两人的速度;
解:设甲的速度为x千米/分,乙的速度为y千米/分.
根据题意,得:10x+10y =5,
所以甲、乙两人的速度是满足上述方程的所有正数解.
(2) 上面的问题(1) 有没有解 如果有解,有多少个解 请写出它的两个解;
有解,
有无数多个解,
如
x =0.1,
y =0.4.
或
x =0.2,
y =0.3.
(3) 请你适当增加上面的问题(1) 中的条件,使问题有唯一解,并解答你改编后的问题.
答案不唯一,所添加的条件是甲的速度比乙的速度快0.1千米/分,此时,有
10x+10y=5,
x=y+0.1.
解得
x =0.3,
y =0.2.
答:甲的速度是0.3千米/分,乙的速度是0.2千米分.
*12. 一个三位数,百位数字比十位数字的2倍多1,个位数字比十位数字的3倍少1. 如果把这个三位数的百位数字和个位数字对调,那么得到的三位数比原来的三位数多99. 求原来的三位数.
解:设十位数字为x,百位数y,个位数为z.
根据题意,得
y=2x+1,
z= 3-1,
100z+10x+y- (100y+10x+z) =99.
解得
x =3,
y =7,
z =8.
答:这个三位数为738.
本课结束!
第10章 一次方程组
青岛版 七年级下册
10 . 4
列方程组解应用题
知识回顾
列一元一次方程解应用题的步骤:
审、列、解、验、答.
交流与发现
长江上一艘游船从沙市港出发,船速为17 千米/时,经过若干小时到达宜昌港.如果船速增加1千米/时,那么用同样多的时间,游船可到达宜昌上游9千米处的葛洲坝.提速前游船由沙市港航行到宜昌港所用的时间是多少 沙市港到宜昌港的航程是多少
在这个问题中,
(1) 已知量是什么 未知量是什么
(2) 等量关系是什么
速度×时间=路程
(3) 如果设游船航行所用的时间为x时,沙市港到宜昌港的航程为y千米你能根据问题中的两个等量关系列出方程组吗
17x = y
(17+1)x = y+9
(4) 你会解所列的方程组吗
17x = y
18x = y+9
进一步整理为:
17x = y
(17+1)x = y+9
例 1
小亮和小莹练习赛跑.如果小亮让小莹先跑 10米,那么小亮跑5秒就追上小莹;如果小亮让小莹先跑 2 秒,那么小亮跑 4秒就追上小莹. 两人每秒各跑多少米
等量关系是:
(1)小亮跑5秒的路程=小莹跑5秒的路程+10米;
(2)小亮跑4秒的路程=小莹跑 (4+2)秒的路程.
解:设小亮每秒跑x米,小莹每秒跑y米.
根据题意,得
5x = 5y +10,
4x = (4+2) y
解得
x = 6,
y= 4.
经检验,方程组的解符合题意.
所以小亮每秒跑6米,小莹每秒跑4米.
例 2
(中国古代数学问题) 有若干只鸡和兔放在同一个笼子里.从上面看,有35个头;从下面看,有94只脚.问笼子里有几只鸡 几只兔
解:设笼子里有x只鸡、y只兔.
已知共有35个头、94只脚.
根据题意,得
x +y = 35 ,
2x +4y = 94.
解得
x = 23,
y= 12.
经检验,方程组的解符合题意.
所以,笼子里有23只鸡、12只兔.
对于这个问题,你能用四则运算的方法和列一元一次方程的方法求解吗 比较这两种方法与列二元一次方程组的方法,你认为它们各有什么特点 与同学交流.
挑战自我
甲、乙二人正在谈论他们的年龄.
甲:在我是你今年的岁数时,你那年10岁.
乙:在我是你今年的岁数时,你那年25岁.
想一想,甲、乙二人谁的年龄大 今年甲、乙二人各多少岁
练 习
1. 为绿化校园,时代中学买了杨树苗和柳树苗共 100棵.杨树苗每棵3 元,柳树苗每棵7元,买树苗共用460 元.两种树苗各买了多少棵
解:设买杨树苗x棵,买柳树苗y棵,
根据题意,得
x +y = 100 ,
3x +7y = 460.
解得
x = 60,
y= 40.
答:买杨树苗60棵,买柳树苗40棵.
2. 如图,用8块相同的长方形瓷砖拼成一个宽为60厘米的长方形灶台面.求每块瓷砖的长和宽 (瓷砖间的缝隙忽略不计 ).
解:设小长方形瓷砖的长为x厘米,宽为y厘米.
根据题意,得
x +y = 60 ,
x =3y.
解得
x = 45,
y= 15.
答:每块瓷砖的长为45厘米,宽为15厘米.
例 3
2010年4月份中国民航国内和国际航线运送旅客总人数共 2 160万人,其中,国内和国际航线运送旅客人数比2009 年4月份分别增长 13.2%和28.8%,2009年4月份国内航线和国际航线运送旅客总人数为1894万人,那么2009 年4月份国内和国际航线运送旅客分别有多少万人(结果精确到万人)
设2009年4月份中国民航国内航线运送旅客x万人,国际航线运送旅客y万人,得到下表:
2009年4月份 2010年4月份
国内航线运送人数/万人 x (1+13.2%)x
国际航线运送人数/万人 y (1+28.8%)y
合计/万人 1894 2160
解:设2009年4月份中国民航国内航线运送旅客x万人,国际航线运送旅客y万人.
根据题意,得
x +y = 1894 ,
(1+13.2%)x+(1+28.8% )y= 2160.
解这个方程组,得
x ≈1791,
y ≈103.
经检验,方程组的解符合题意.
所以2009年4月份中国民航国内航线运送旅客1791万人,国际航线运送旅客103万人
加油站
在解决一类实际问题时,可以通过列出方程组表示问题中的全部数量关系,所以方程组也是刻画现实世界数量关系的有效模型.
例 4
果园要将一批水果运往某地,打算租用某汽车运输公司的甲、乙两种货车.过去两次租用这两种货车的信息如下表所示:
第一次 第二次
甲种货车车辆数 /辆 2 5
乙种货车车辆数 /辆 3 6
累计运货量/吨 15.5 35
现打算租用该公司 3 辆甲种货车和 5 辆种货车,可一次刚好运完这批水果.如果每吨运费为30元,果园应付运费多少元
等量关系是:
(1) 2辆甲种货车运量+3辆乙种货车运量=15.5吨;
(2) 5辆甲种货车运量+6辆乙种货车运量=35吨
根据题意,得
2x + 3y = 15.5 ,
5x + 6y = 35.
解得
x =4,
y =2.5.
经检验,方程组的解符合题意.
这次运水果所需运费为30×(4×3+2.5×5) =735(元)
所以,果园应付运费735元
智趣园
两鼠穿墙
《九章算术》提出了一个有趣的问题:“今有垣厚五尺,两鼠对穿,大鼠日一尺,小鼠也日一尺.大鼠日自倍,小鼠日自半,问何日相逢,各穿几何 ”
意思是说:今有一道墙,厚5尺,两只老鼠从墙的两边分别打洞穿墙.大老鼠第一天进一尺,以后每天的进度是前一天的2倍;小老鼠第一天也进1尺,以后每天的进度是前一天的一半.问几天后两鼠相遇;此时.两鼠各穿墙几尺
该题当初是用“盈不足术”求解的.学过一次方程组后,我们也可以用二元一次方程组求解.由题意可知,穿墙第一天,大鼠、小鼠各穿墙1尺,共2尺;穿墙第二天,大鼠穿墙2尺,小鼠穿墙尺.两天大鼠和小鼠共穿墙尺,离穿透墙尚差尺.到第三天时,不用1天二鼠即可相遇.
在穿墙的第三天,设大鼠前进了x尺,小鼠前进了y尺,大鼠该天穿墙速度为4尺/天,小鼠为尺/天.等量关系是:①大鼠、小鼠一共穿墙尺;②该天在相遇前大、小鼠用的时间相等.
你能根据以上分析列出二元一次方程组来求解吗
练 习
1. 时代中学师生 100 人到甲、乙两公司参加社会实践活动,到甲公司的人数比到乙公司的人数的2倍少8 人,到两公司参加社会实践的人数各多少
解:设到乙公司参加社会实践活动的有x人,则到甲公司参加社会实践活动的有(2x-8)人,
根据题意得,(2x-8) +x =100,
解得 x=36
则 2x-8=2×36-8=64.
答:到甲公司参加社会实践活动的有64人,到乙公司参加社会实践活动的有36人.
2. 山青林场有一块面积为 58 公顷的土地,现计划将其中的开辟为果园,其余的土地种粮食和蔬菜,并且种蔬菜的土地面积是种粮食的土地面积的. 该林场计划种蔬菜和粮食各多少公顷
解:设计划种蔬菜x公顷,种粮食y公顷,
根据题意,得
x + 3= 58×(1-) ,
x = y.
解得
x =8.7,
y =34.8.
答:该农场计划种蔬菜8.7公顷,种粮食34.8公顷.
例 5
一个三位数,三位数字之和为 12,个位数字是百位数字与十位数字之和的2倍,百位数字是十位数字的3倍,求这个三位数.
解:设这个三位数的个位数字为x,十位数字为y,百位数字为z.
根据题意,得
x+y+z = 12,
x = 2(y+z)
z = 3y.
解得
x =8,
y =1,
z =3.
经检验,方程组的解符合题意.
所以这个三位数是318.
* 例 6
(中国古代数学问题)今有上等黍3捆,中等黍2捆,下等黍 1捆,共打出黍米39斗;又有上等黍2捆,中等黍3捆,下等黍1捆,共打出黍米34斗;再有上等黍1捆,中等黍2捆,下等黍3捆,共打出黍米26斗.问每捆上、中、下黍各能打出黍米多少斗
解:设每捆上、中、下黍分别能打出黍米x斗、y斗、z斗.
根据题意,得
3x+2y+z = 39,
2x+3y+z= 34,
x+2y+3z= 26.
解得
x =,
y = ,
z = .
经检验,方程组的解符合题意.
所以,每捆上、中、下泰分别能打出黍米斗、 斗、 斗.
挑战自我
小亮、小莹和大刚每人面前各放有一堆栗子.小亮将自己面前的栗子分出一些给另外二人后,这二人的栗子数各增加1倍.接着小莹又将自己面前的栗子分些给小亮和大刚,小亮和大刚的栗子数都增加了1倍.
然后,大刚又分给另外二人一些栗子,使小亮和小莹面前的栗子数也都增加1倍. 这时,他们三人面前的栗子竟然都是 24颗.
你知道他们三人面前原来各有多少颗栗子吗
史海漫游
古老的百鸡问题
公元5世纪左右,北魏时期的数学家张丘建在他所著的《 张丘建算经 》中提出了一个著名的“百鸡问题”;
《张丘建算经》 (宋刻本 )
关于百鸡问题的记载
(选自《中国大百科全书·数学》)
《张丘建算经》 (宋刻本 )
关于百鸡问题的记载
(选自《中国大百科全书·数学》)
“今有鸡翁一,直钱五;鸡母一,直钱三;鸡雏三,直钱一.凡百钱买鸡百只,问鸡翁、母、雏各几何 ”
《张丘建算经》 (宋刻本 )
关于百鸡问题的记载
(选自《中国大百科全书·数学》)
题目大意是:一只公鸡价值 5钱 (我国古代的一种货币单位),一只母鸡价值3 钱,三只维鸡价值 1钱.用100钱买了100只鸡,问买公鸡、母鸡和雏鸡各多少只.
这一问题可利用列方程组的方法解决. 设x,y,z 分别表示所买公鸡、母鸡、雏鸡的只数,根据题意,得
这个方程组中有两个方程,却有三个未知数. 这类方程组在数学上称为不定方程组. 本题是求一个三元一次不定方程组的正整数解问题. 这一问题的提出标志着我国在公元5世纪时已对不定方程组有了系统深入的研究,并为后人学习不定方程组的求解提供了一个入门的范例.
利用我们学过的知识,可以采用下面的方法解这个不定方程组:
由②×3-①,化简得
7x+4y=100 .
y=25-x .
因为y是正整数,所以x应是4的整数倍,且 (25- x) 也是正整数,所以x只能取4,8,12. 由此得
所以,公鸡、母鸡、雏鸡各买了4只、18只、78只;或8只、11只、81只;或12只、4只、84只.
练 习
*1.甲、乙、丙三个数的和是25,甲数的等于乙数的,甲数比乙数与丙数的和少1.求这三个数.
解:设甲数为x,乙数为y,丙数为z.
根据题意,得
x + y + z = 25,
x = y,
y + z - x = 1.
解得
x =12,
y =8,
z =5.
答:甲数为12,乙数为8,丙数为5.
*2. 某市举行中学生足球联赛,比赛的计分规则为:胜一场得3 分,平一场得1分,负一场得0分. 时代中学足球队在12场比赛中,平和负
的场数之和等于胜的场数,共
积21分.这个队在这届联赛中胜、
平、负各几场
解:设这个队在这届联赛中胜、平、负各x场、y场、z场.
根据题意,得
x + y + z = 12,
y +z= ,
3x+y = 21.
解得
x =6,
y =3,
z =3.
答:这个队在这届联赛中胜、平、负各6场、3场、3场.
习题 10.4
复习与巩固
1. (中国古代数学问题)几个合作经营的商人正分配所得银两,某人在隔壁听见他们说,如果每人分得7两,就剩下4两; 如果每人分得9两,还少半斤 (旧时1斤= 16两).你知道共有多少商人和多少银两吗
解:设共有商人x人和银两y两,
根据题意,得
7x +4 = y ,
9x-8= y.
解得
x =6,
y =46.
经检验,方程组的解符合题意.
答:共有商人6人,银两46两.
2.“十一”黄金周期间,某景区共接待省内、外游客122万人,总收入达4.8亿元,其中省内、外游客人均消费分别为160元和1200元.该景区接待省内、外游客各多少万人(精确到1万人)
解:设省内旅游者x万人次,省外旅游者y万人次,
根据题意,得
x +y =122 ,
160x+1200y=4 8000 0000.
解得
x ≈46 ,
y ≈72.
答:该景区接待省内外游客各为46和72万人.
3. 每千克大豆饼和棉籽饼中,磷和钾的含量(单位:克)分别如下表所示:
磷 钾
大豆饼 13.2 21.3
棉籽饼 16.3 9.7
现在要用这两种肥料配制成含磷 45.8 千克、钾40.7 千克的混合肥料.大豆饼和棉籽饼各需多少千克
解:设需要大豆饼x,棉籽饼y.
根据题意,得
13.2x+16.3y =45.8,
21.3x+9.7y=40.7.
解得
x =10,
y =20.
故配置成含磷45.8千克,含40.7千克的混合肥料需要大豆饼10千克棉籽饼20千克.
4. 暑假时一批中学生参加夏令营,途经某旅店住宿.如果每间客房安排住7人,就会有7人没有地方住;如果每间客房安排住9人,就会空出一间房. 求旅店的客房数和中学生的人数.
解:设旅店的客房数为x间,中学生的人数为y人.
根据题意,得
7x+7 = y,
9(x-1)=y.
解得
x =8,
y =63.
答:旅店的客房数为8间,中学生的人数为63人.
5. 某开发区去年的出口创汇额为25 亿美元,今年达到30.55 亿美元.已知今年上半年的出口创汇额比去年同期增长 18%,下半年比去年同期增长 25%,求今年上半年和下半年的出口创汇额.
解:设去年上半年出口创汇额为x亿美元,去年下半年的出口创汇额为y亿美元.
则今年上半年出口创汇额为:
(1+18%) x=1.18x (亿美元),
今年下半年的出口创汇额为:
(1+25%)y=1.25y (亿美元),
根据题意,得
x+y = 25,
1.18z +1.25y=30.55.
解得
x =10,
y =15.
1.18x=11.8亿美元,1.25y=18.75亿美元,
答:今年上半年的出口创汇额11.8亿美元,下半年的出口创汇额18.75亿美元
6. 张大婶和王姐去菜市场买菜. 张大婶买了土豆3千克、菠菜2千克,共花费10.2元;王姐买了芹菜1千克、土豆2千克、菠菜1千克,共花费9.2元. 已知芹菜每千克3元,问土豆和菠菜每千克各多少元.
解:设土豆每千克x元,菠菜每千克y元,
根据题意,得
3x +2y =10.2,
3+2x+y=9.2.
解得
x =2.2,
y =2.
答:故土豆每千克2.2元,菠菜每千克2元.
拓展与延伸
7.一张方桌由一个桌面和四条桌腿组成. 如果1立方米木料可制作桌面 50个,或制作桌腿300条. 现有5立方米木料,请你设计一下,用多少木料做桌面,用多少木料做桌腿,恰好配成方桌多少张
解:设用xm3木料做桌面,则用ym3木料做桌腿,恰好配成方桌,
根据题意,得
4×50x =300y,
x+y=5.
解得
x =3,
y =2.
50×3=150张
∴用3m3木料做桌面,用2m3木料做桌腿,恰好配成方桌150张.
*8. (中国古代问题)买2匹马、3头牛或4只羊,价钱分别都不满10 000文(古时货币单位). 如果买2匹马加上1头牛,或者买3头牛加上1只羊,或者买4只羊加上1匹马,那么各自的价钱正好都是10 000文.求马、牛、羊的单价.
解:设1匹马的价格为x文,1头牛的价格为y文,1只羊的价格为z文.
根据题意,得
2x +y =10000,
3y+z=10000,
4z+x=10000.
解得
x =3600,
y =2800,
z=1600.
答:1匹马的价格为3600文,1头牛的价格为2800文,1只羊的价格为1600文.
*9.某公路收费站对过往车辆的收费标准是:大客车30元,小客车15元,小轿车 10元. 某天通过该收费站的大客车是小客车数量的,小客车是小轿车数量的,收取小轿车的通行费比大客车和小客车通行费之和少1050元.求当天这三种车辆通过的数量.
解:设当天通过该收费站的小轿车有x辆,则当天通过该收费站的小客车有x辆,大客车有 ×x =x辆,
依题意,得: 30×x+15×x-10x = 1050,
解得:x = 231,
∴ x =84, x =70.
答:当天通过该收费站的小轿车有231辆,小客车有84辆,大客车有70辆.
10.《一千零一夜》中有这样一段文字: 有一群鸽子,其中一部分在树上欢歌,另一部分在地上觅食.树上的一只鸽子对地上的鸽子说:“如果从你们中飞上来一只,那么树下的鸽子是整个鸽群的;如果从树上飞下去一只,树上、树下的鸽子就一样多.”你知道原来树上、树下的鸽子各多少只
解:设树上有x只鸽子,树下有y只鸽子.
根据题意,得
y-1 =(x+y),
x+1=y+ 1.
解得
x =7,
y =5.
答:树上原有7只鸽子,树下有5只鸽子。
根据题意,得
2y-x =3,
y=x-2.
探索与创新
11. 甲、乙二人骑自行车同时从相距5千米的两地相向而行,经过 10分钟相遇.
(1) 求甲、乙两人的速度;
解:设甲的速度为x千米/分,乙的速度为y千米/分.
根据题意,得:10x+10y =5,
所以甲、乙两人的速度是满足上述方程的所有正数解.
(2) 上面的问题(1) 有没有解 如果有解,有多少个解 请写出它的两个解;
有解,
有无数多个解,
如
x =0.1,
y =0.4.
或
x =0.2,
y =0.3.
(3) 请你适当增加上面的问题(1) 中的条件,使问题有唯一解,并解答你改编后的问题.
答案不唯一,所添加的条件是甲的速度比乙的速度快0.1千米/分,此时,有
10x+10y=5,
x=y+0.1.
解得
x =0.3,
y =0.2.
答:甲的速度是0.3千米/分,乙的速度是0.2千米分.
*12. 一个三位数,百位数字比十位数字的2倍多1,个位数字比十位数字的3倍少1. 如果把这个三位数的百位数字和个位数字对调,那么得到的三位数比原来的三位数多99. 求原来的三位数.
解:设十位数字为x,百位数y,个位数为z.
根据题意,得
y=2x+1,
z= 3-1,
100z+10x+y- (100y+10x+z) =99.
解得
x =3,
y =7,
z =8.
答:这个三位数为738.
本课结束!
同课章节目录
- 第8章 角
- 8.1 角的表示
- 8.2 角的比较
- 8.3 角的度量
- 8.4 对顶角
- 8.5 垂直
- 第9章 平行线
- 9.1 同位角、内错角、同旁内角
- 9.2 平行线和它的画法
- 9.3 平行线的性质
- 9.4 平行线的判定
- 第10章 一次方程组
- 10.1 认识二元一次方程组
- 10.2 二元一次方程组的解法
- 10.3 三元一次方程组
- 10.4 列方程组解应用题
- 第11章 整式的乘除
- 11.1 同底数幂的乘法
- 11.2 积的乘方与幂的乘方
- 11.3 单项式的乘法
- 11.4 多项式乘多项式
- 11.5 同底数幂的除法
- 11.6 零指数幂与负整数指数幂
- 第12章 乘法公式与因式分解
- 12.1 平方差公式
- 12.2 完全平方公式
- 12.3 用提公因式法进行因式分解
- 12.4 用公式法进行因式分解
- 第13章 平面图形的认识
- 13.1 三角形
- 13.2 多边形
- 13.3 圆
- 第14章 位置与坐标
- 14.1 用有序数对表示位置
- 14.2 平面直角坐标系
- 14.3 直角坐标系中的图形
- 14.4 用方向和距离描述两个物体的相对位置
