初中数学青岛版 七年级下册11.3 单项式的乘法课件(共45张PPT)
文档属性
| 名称 | 初中数学青岛版 七年级下册11.3 单项式的乘法课件(共45张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 60.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-11 00:00:00 | ||
图片预览










文档简介
(共45张PPT)
第11章 整式的乘除
青岛版 七年级下册
11 . 3
单项式的乘法
交流与发现
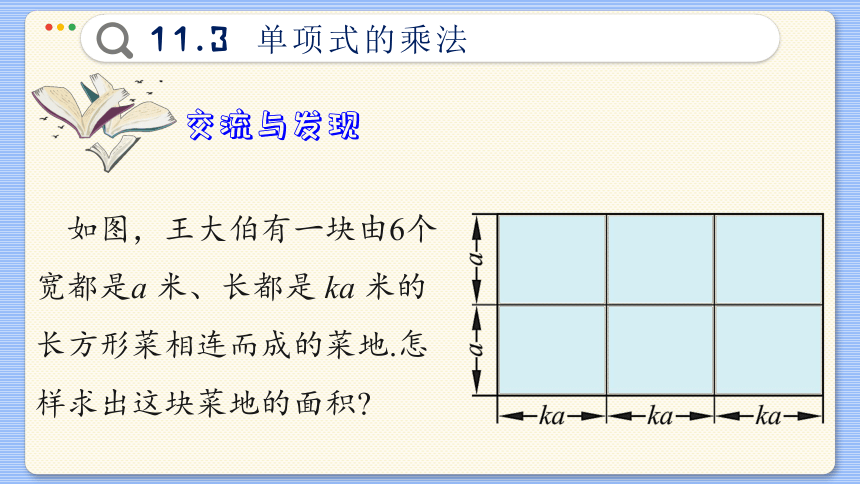
如图,王大伯有一块由6个宽都是a 米、长都是 ka 米的长方形菜相连而成的菜地.怎样求出这块菜地的面积
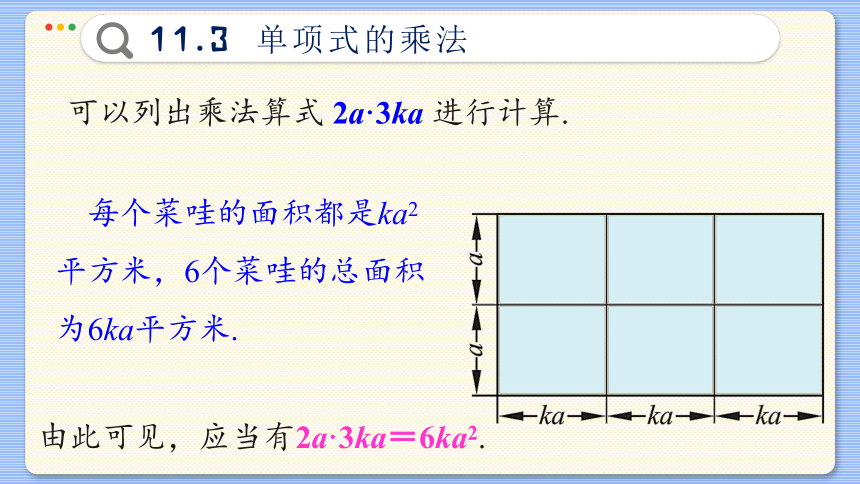
可以列出乘法算式 2a·3ka 进行计算.
每个菜哇的面积都是ka2平方米,6个菜哇的总面积为6ka平方米.
由此可见,应当有2a·3ka=6ka2.
2a·3ka=6ka2
观察上面得到的等式,你发现它的左边与右边有什么特点
2a·3ka=6ka2
上面等式的左边是两个单项式相乘,等式右边的单项式就是左边两个单项式的积.
如果按照乘法的交换律、结合律和同底数幂的乘法性质,也可以得到
2a·3ka= (2×3)ka·a=6ka2
2a·3ka= (2×3)ka·a=6ka2
这里得到的单项式2a与3ka的乘积6ka2,与上面由实际问题得到的等式是一致的.
这就是说,两个单项式相乘,可以按照乘法的运算律,转化为有理数的乘法和同底数幂的乘法进行运算.
一般地,单项式与单项式相乘有以下法则:
单项式相乘,把它们的系数相乘,字母部分的同底数幂分别相乘.
对于只在一个单项式中含有的字母,连同它的指数作为积的一个因式.
例 1
计算:
(1) 4a3·7a4; (2) 7ax·(-2a2bx2).
(1) 4a3.7a4 = (4×7)·(a3·a4) =28a7;
(2) 7ax·(-2a2bx2) =[7× (-2)]·(a·a2)·b·(x·x2)
=-14a3bx3.
例 2
求单项式 的积.
x3y2.(- xy3z)·x2yz2
=[×(- )×]·(x3·x·x2)·(y2·y3·y)·(z·z2)
=- x6y6z3
练 习
1.计算:
= 3×4x2+1
= 12x3
= -3×x1+3y2+1z
= -x4y3z
= -×+15a2bx5y
= -a2bx5y
= 4a2·a6 = 4a8
2. 下列计算对不对 如果不对,应怎样改正
(1) 2x3·3x2=6x6;
(2) 2x3+3x2=5x5;
(3) (-2ab)·3bc=-6abc;
(4) (-xy)·(-3xy)2= -12x3y3.
6x5
2x3与3x2不能合并
-6ab2c
遇到积的乘方怎么办?运算时应先算什么?
(1) 先做乘方,再做单项式相乘。
(2)系数相乘不要漏掉负号
交流与发现
如图,如果王大伯家的菜地两侧各有一条宽0.5 米的小路.怎样求出包括小路在内的菜地的面积
可以列出乘法算式 2a·(3ka+1) 进行计算.
这块地面积为6个菜哇的面积和两段小路面积的和,即6ka2+2a.
2a·(3ka+1) =6ka2+2a.
2a·(3ka+1) =6ka2+2a.
观察上面得到的等式,你发现它的左边与右边有什么特点
2a·(3ka+1) =6ka2+2a.
上面等式的左边是一个单项式与一个多项式相乘,右边是这个单项式与这个多项式的积.
按照乘法对加法的分配律和单项式的乘法法则,得到
2a·(3ka +1) =2a·3ka+2a·1 = 6ka2+2a.
2a·(3ka +1) =2a·3ka+2a·1 = 6ka2+2a.
这里得到的单项式2a与多项式 3ka+1 的积,与上面由实际问题得到的等式是一致的.
这就是说,单项式与多项式相乘可以按照乘法对于加法的分配律,转化成单项式的乘法进行.
一般地,单项式与多项式相乘有以下法则:
单项式与多项式相乘,先将单项式分别乘多项式的各项,再把所得的积相加.
例 3
计算:2ax·(3a2x - 2a2x2).
2ax·( 3a2x-2a2x2)
= 2ax·3a2x -2ax·2a2x2
= 6a3x2-4a3x3.
例 4
化简:x·(x-y+z)+(x-y-z)·y-z·(x-y+z).
x·(x-y+z)+(x-y-z)·y-z·(x-y+z)
=(x2-xy+xz) +(xy-y2 - yz)-(xz-z+z2)
=x2-xy+xz+xy-y2-yz-xz+yz-z2
=x2-y2-z2.
练 习
1. 计算:
(1) 3x·(x2+x+2);
(2) -a2·(a+b)+b·(a2-b2).
= -a3-a2b+a2b-b3
= -a3-b3.
= 3x3+3x2+6x
(2) -a2·(a+b)+b·(a2-b2).
= -a3-a2b+a2b-b3
= -a3-b3.
2. 下列计算对不对 如果不对,应怎样改正
(1) (5x2y-2xy2 )·3x =15x2y - 6xy2;
(2) (-2t)·(3t+t2-1) = -6t2-2t3+2;
(3) (-xy2)·(-3xy+9yz-1) =x2y3-3xy3z-xy2;
(4) an(2an-3an-1+a) = 2a2n-3a2n-1+an+1.
15x3y - 6x2y2
-6t2-2t3+2t
x2y3-3xy3z + xy2
习题 11.3
复习与巩固
1. 计算:
(1) 4a3·8a2; (2) 2x2y2z·3xyz3·y5z;
(3) 2ab2·3a2bc2; (4) (-4x2y)·(-5xy3).
=32a5
=6x3y8z5
=6a3b3c3
=20x3y4
2. 计算:
= -1.2×5×3×103+2+7
=-18×1012
= -1.8×1013
= ()8×(102)8×35×(103)5
= ×106×35×1015
= ×106+5+15
=×1031
= - ab2c·(-5)3·(a2)3·b3
=-ab2c·(-53) ·a6·b3
= 25a7b5c
= 16x8y2·(-x5y15)
=-16x8+5y2+15
=-16x13y17
3. 计算:
= 2x·(-4x)+(- )×(-4x)
=-8x2 +2x
= 3xy ·x2y-3xy ·xy
= 3x3y2 - 3x2y2
4. 化简:
= 3a2-10a-3a2
= -10 a
= t2+4t+3t2+3
= t4+4t+3
=-(-2x3+4x2-2x)
=2x3-4x2+2x
=-( b2 ·3a2 -ab ·3a2 - ·3a2)
= -(a2b2 -2a3b -4a2)
= -a2b2+2a3b+4a2,
5. 先化简,再求值:
原式= x4-x3+x2-x4+x3-x2+x
= x,
原式=.
原式= x3+x-x3+3x2-3x2-3x+3
=-2x+3 ,
将 x= 代入-2x+3 计算得,
故原式= .
拓展与延伸
6. 计算:
= 32·x2·y2×2 +[(-4)×(-1)]·(x·x)·(y·y)
=9x2y4 +4x2y4
=(9+4)x2y4
=13x2y4
= t3-2t (t2-2t+6)
= t3- (2t3-4t2+12t )
= t3-2t3-4t2 - 12t
= - t3+4t2-12t
7. 解下列方程:
解:6x2-6x2-4x+9x =-10
5x=-10
x=-2.
解:24x-78x2+54x =-13-78x2+13x
68x=-13,
x=-.
探索与创新
8. 如图,梯形ABCD的下底长为a,上底长为b,四边形ABEF是正方形.用多项式表示图中黄色图形的面积.
∵ 四边形ABEF是正方形
∴ AB=AF,∠AFC =90°
∵ 上底长为b,
∴ AB=AF=b·
∵下底长为a
∴S梯形ABCD==
∵ 四边形ABEF是正方形
∴ S四边形ABEF =b2,
∴S黄色图形=S梯形ABCD -S四边形ABEF
= - b2
=
本课结束!
第11章 整式的乘除
青岛版 七年级下册
11 . 3
单项式的乘法
交流与发现
如图,王大伯有一块由6个宽都是a 米、长都是 ka 米的长方形菜相连而成的菜地.怎样求出这块菜地的面积
可以列出乘法算式 2a·3ka 进行计算.
每个菜哇的面积都是ka2平方米,6个菜哇的总面积为6ka平方米.
由此可见,应当有2a·3ka=6ka2.
2a·3ka=6ka2
观察上面得到的等式,你发现它的左边与右边有什么特点
2a·3ka=6ka2
上面等式的左边是两个单项式相乘,等式右边的单项式就是左边两个单项式的积.
如果按照乘法的交换律、结合律和同底数幂的乘法性质,也可以得到
2a·3ka= (2×3)ka·a=6ka2
2a·3ka= (2×3)ka·a=6ka2
这里得到的单项式2a与3ka的乘积6ka2,与上面由实际问题得到的等式是一致的.
这就是说,两个单项式相乘,可以按照乘法的运算律,转化为有理数的乘法和同底数幂的乘法进行运算.
一般地,单项式与单项式相乘有以下法则:
单项式相乘,把它们的系数相乘,字母部分的同底数幂分别相乘.
对于只在一个单项式中含有的字母,连同它的指数作为积的一个因式.
例 1
计算:
(1) 4a3·7a4; (2) 7ax·(-2a2bx2).
(1) 4a3.7a4 = (4×7)·(a3·a4) =28a7;
(2) 7ax·(-2a2bx2) =[7× (-2)]·(a·a2)·b·(x·x2)
=-14a3bx3.
例 2
求单项式 的积.
x3y2.(- xy3z)·x2yz2
=[×(- )×]·(x3·x·x2)·(y2·y3·y)·(z·z2)
=- x6y6z3
练 习
1.计算:
= 3×4x2+1
= 12x3
= -3×x1+3y2+1z
= -x4y3z
= -×+15a2bx5y
= -a2bx5y
= 4a2·a6 = 4a8
2. 下列计算对不对 如果不对,应怎样改正
(1) 2x3·3x2=6x6;
(2) 2x3+3x2=5x5;
(3) (-2ab)·3bc=-6abc;
(4) (-xy)·(-3xy)2= -12x3y3.
6x5
2x3与3x2不能合并
-6ab2c
遇到积的乘方怎么办?运算时应先算什么?
(1) 先做乘方,再做单项式相乘。
(2)系数相乘不要漏掉负号
交流与发现
如图,如果王大伯家的菜地两侧各有一条宽0.5 米的小路.怎样求出包括小路在内的菜地的面积
可以列出乘法算式 2a·(3ka+1) 进行计算.
这块地面积为6个菜哇的面积和两段小路面积的和,即6ka2+2a.
2a·(3ka+1) =6ka2+2a.
2a·(3ka+1) =6ka2+2a.
观察上面得到的等式,你发现它的左边与右边有什么特点
2a·(3ka+1) =6ka2+2a.
上面等式的左边是一个单项式与一个多项式相乘,右边是这个单项式与这个多项式的积.
按照乘法对加法的分配律和单项式的乘法法则,得到
2a·(3ka +1) =2a·3ka+2a·1 = 6ka2+2a.
2a·(3ka +1) =2a·3ka+2a·1 = 6ka2+2a.
这里得到的单项式2a与多项式 3ka+1 的积,与上面由实际问题得到的等式是一致的.
这就是说,单项式与多项式相乘可以按照乘法对于加法的分配律,转化成单项式的乘法进行.
一般地,单项式与多项式相乘有以下法则:
单项式与多项式相乘,先将单项式分别乘多项式的各项,再把所得的积相加.
例 3
计算:2ax·(3a2x - 2a2x2).
2ax·( 3a2x-2a2x2)
= 2ax·3a2x -2ax·2a2x2
= 6a3x2-4a3x3.
例 4
化简:x·(x-y+z)+(x-y-z)·y-z·(x-y+z).
x·(x-y+z)+(x-y-z)·y-z·(x-y+z)
=(x2-xy+xz) +(xy-y2 - yz)-(xz-z+z2)
=x2-xy+xz+xy-y2-yz-xz+yz-z2
=x2-y2-z2.
练 习
1. 计算:
(1) 3x·(x2+x+2);
(2) -a2·(a+b)+b·(a2-b2).
= -a3-a2b+a2b-b3
= -a3-b3.
= 3x3+3x2+6x
(2) -a2·(a+b)+b·(a2-b2).
= -a3-a2b+a2b-b3
= -a3-b3.
2. 下列计算对不对 如果不对,应怎样改正
(1) (5x2y-2xy2 )·3x =15x2y - 6xy2;
(2) (-2t)·(3t+t2-1) = -6t2-2t3+2;
(3) (-xy2)·(-3xy+9yz-1) =x2y3-3xy3z-xy2;
(4) an(2an-3an-1+a) = 2a2n-3a2n-1+an+1.
15x3y - 6x2y2
-6t2-2t3+2t
x2y3-3xy3z + xy2
习题 11.3
复习与巩固
1. 计算:
(1) 4a3·8a2; (2) 2x2y2z·3xyz3·y5z;
(3) 2ab2·3a2bc2; (4) (-4x2y)·(-5xy3).
=32a5
=6x3y8z5
=6a3b3c3
=20x3y4
2. 计算:
= -1.2×5×3×103+2+7
=-18×1012
= -1.8×1013
= ()8×(102)8×35×(103)5
= ×106×35×1015
= ×106+5+15
=×1031
= - ab2c·(-5)3·(a2)3·b3
=-ab2c·(-53) ·a6·b3
= 25a7b5c
= 16x8y2·(-x5y15)
=-16x8+5y2+15
=-16x13y17
3. 计算:
= 2x·(-4x)+(- )×(-4x)
=-8x2 +2x
= 3xy ·x2y-3xy ·xy
= 3x3y2 - 3x2y2
4. 化简:
= 3a2-10a-3a2
= -10 a
= t2+4t+3t2+3
= t4+4t+3
=-(-2x3+4x2-2x)
=2x3-4x2+2x
=-( b2 ·3a2 -ab ·3a2 - ·3a2)
= -(a2b2 -2a3b -4a2)
= -a2b2+2a3b+4a2,
5. 先化简,再求值:
原式= x4-x3+x2-x4+x3-x2+x
= x,
原式=.
原式= x3+x-x3+3x2-3x2-3x+3
=-2x+3 ,
将 x= 代入-2x+3 计算得,
故原式= .
拓展与延伸
6. 计算:
= 32·x2·y2×2 +[(-4)×(-1)]·(x·x)·(y·y)
=9x2y4 +4x2y4
=(9+4)x2y4
=13x2y4
= t3-2t (t2-2t+6)
= t3- (2t3-4t2+12t )
= t3-2t3-4t2 - 12t
= - t3+4t2-12t
7. 解下列方程:
解:6x2-6x2-4x+9x =-10
5x=-10
x=-2.
解:24x-78x2+54x =-13-78x2+13x
68x=-13,
x=-.
探索与创新
8. 如图,梯形ABCD的下底长为a,上底长为b,四边形ABEF是正方形.用多项式表示图中黄色图形的面积.
∵ 四边形ABEF是正方形
∴ AB=AF,∠AFC =90°
∵ 上底长为b,
∴ AB=AF=b·
∵下底长为a
∴S梯形ABCD==
∵ 四边形ABEF是正方形
∴ S四边形ABEF =b2,
∴S黄色图形=S梯形ABCD -S四边形ABEF
= - b2
=
本课结束!
同课章节目录
- 第8章 角
- 8.1 角的表示
- 8.2 角的比较
- 8.3 角的度量
- 8.4 对顶角
- 8.5 垂直
- 第9章 平行线
- 9.1 同位角、内错角、同旁内角
- 9.2 平行线和它的画法
- 9.3 平行线的性质
- 9.4 平行线的判定
- 第10章 一次方程组
- 10.1 认识二元一次方程组
- 10.2 二元一次方程组的解法
- 10.3 三元一次方程组
- 10.4 列方程组解应用题
- 第11章 整式的乘除
- 11.1 同底数幂的乘法
- 11.2 积的乘方与幂的乘方
- 11.3 单项式的乘法
- 11.4 多项式乘多项式
- 11.5 同底数幂的除法
- 11.6 零指数幂与负整数指数幂
- 第12章 乘法公式与因式分解
- 12.1 平方差公式
- 12.2 完全平方公式
- 12.3 用提公因式法进行因式分解
- 12.4 用公式法进行因式分解
- 第13章 平面图形的认识
- 13.1 三角形
- 13.2 多边形
- 13.3 圆
- 第14章 位置与坐标
- 14.1 用有序数对表示位置
- 14.2 平面直角坐标系
- 14.3 直角坐标系中的图形
- 14.4 用方向和距离描述两个物体的相对位置
