初中数学青岛版 七年级下册11.6 零指数幂与负整数指数幂课件(共85张PPT)
文档属性
| 名称 | 初中数学青岛版 七年级下册11.6 零指数幂与负整数指数幂课件(共85张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 65.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-11 19:28:14 | ||
图片预览











文档简介
(共85张PPT)
第11章 整式的乘除
青岛版 七年级下册
11 . 6
零指数幂与负整数指数幂
复习提问
回忆正整数指数幂的运算性质:
(m,n是正整数);
(2) 幂的乘方:
(m,n是正整数);
(1) 同底数的幂的乘法:
(3) 积的乘方:
(n是正整数);
(4) 同底数的幂的除法:
( a≠0,m,n是正整数,m>n);
(5) 商的乘方:
(n是正整数);
2、am÷an=am-n ( a≠0,m,n是正整数,m>n);
在同底数幂的除法公式时,有一个附加条件:m>n,即被除数的指数大于除数的指数.
当被除数的指数不大于除数的指数,即m=n或m<n时,情况怎样呢?
观察与思考
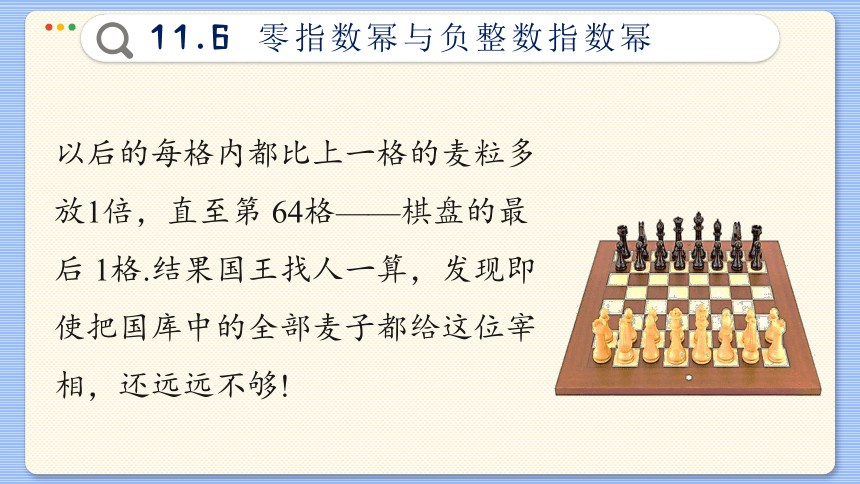
(1) 你听说过这样一个故事吗 古印度舍罕国王打算重赏国际象棋发明者宰相西萨. 西萨要求在棋盘的第1个格内只赏 1粒麦子,在第 2个格内只赏2粒,第3 个格内只赏4粒,
以后的每格内都比上一格的麦粒多放1倍,直至第 64格——棋盘的最后 1格.结果国王找人一算,发现即使把国库中的全部麦子都给这位宰相,还远远不够!
在这个故事中,从第2个格开始,各方格的麦粒数都可以写成底数是2的正整数指数幂的形式,如下表所示:
方格序号 1 2 3 4 5 ··· 64
麦粒个数 1 21 22 23 24 ··· 263
能把第1个格内的麦粒数也写成底数为2的幂的形式吗
方格序号 1 2 3 4 5 ··· 64
麦粒个数 1 21 22 23 24 ··· 263
按照表中的规律,第1个格中的麦粒数用底数是2的幂表示,应写成 20,不过,这样就出现零指数了.
“20=1”,这在数学上合理吗
(2) 观察除式 23÷23,你发现被除式和除式有哪些特点 如何计算它们的商?
由于被除数和除数相等,因此它们的商等于1,即
23÷23= 1.
为了使被除式的指数等于除式的指数时,同底数幂除法的运算性质也能使用,应当规定20=1.
如果仿照同底数幂除法的运算性质进行计算,就得:
23÷23=23-3=20.
(3) 一般地,为了使同底数幂的除法性质 am÷an=
am-n (m,n 是正整数,m>n,a≠0) 当m=n 时也成立,你认为应对零指数幂的意义作怎样的规定
a0=1 (其中a≠0)
这就是说,
任何不等于零的数的零次幂等于1,
零的零次幂没有意义.
这样一来,幂指数的范围从正整数扩充到全体自然数了.
例如,100=1,(-)0 = 1.你能再举出几个数的零次幂的例子吗
(4) 在上面的规定中,为什么有a≠0的限制 与同学交流.
例 1
计算:2x0 (x=0).
2x0=2× 1 = 2.
例 2
计算:a2÷a0·a2 (a≠0).
a2÷a0 · a2=a2÷l · a2=a2 · a2=a4
想一想,a2÷ (a0 · a2)等于什么
练 习
1. 计算:
(1) 60 ; (2) (-8)0;
(3) (x-y)0(x≠y); (4) ×(-)0
=1
=1
=1
=
(5) ( 100×20) ÷(10 ×20); (6) 103÷100× 105.
=(100×1)2 ÷ (10×1)2
= 100 ÷ 10
= 10
=103-0+5
= 108
2. 填空(在方框内填上合适的数 ):
(1) a2÷a =a ( a ≠ 0);
(2) x · x2 · x = x5 · x0 ( x ≠ 0 ).
0
3
3. 当a为怎样的有理数时,(a - 1)0 = 1
观察与思考
(1) 如图,数轴上点A表示的数是8,一动点P从点A出发,向左按以下规律跳动:第1次跳动到OA的中点A1处,第2次从A1点跳动到OA1的中点A2,处,第3次从A2点跳动到 OA2,的中点A3处.
如果把点A表示的数写成23,那么点A1,A2,A3应怎样分别用底数是2的幂的形式表示
点 A,A1,A2,A3依次可以写成23,22,21,20,
这里23=8,22=4,21=2,20=1.
(2) 如果动点P按(1)中的规律继续向左跳动到点 A4,A5,A6,···处,你能把点 A4,A5,A6 所表示的数写成2的整数指数幂的形式吗 它们应当分别等于多少
按照上面的规律,点A4,A5,A6 所表示的数写成底数是2的幂的形式,应分别是 2-1,2-2,2-3. 不过,这样就出现负整数指数幂了.
按照上面的规律,点A4,A5,A6 所表示的数分别是,,· 应当有2-1 = ,2-2= ,2-3= . 这在数学上合理吗
(3) 观察除式22÷23 和22÷24.你发现被除式和除式有哪些特点 如何计算它们的商
由分数的意义和约分法则,得:
如果仿照同底数幂除法的运算性质进行计算,就得
22÷23=22-3 = 2-1;
22÷24=22-4=2-2
为了使被除式的指数小于除式的指数时,同底数幂除法的运算性质也能使用,应当规定
2-1 = ,2-2= ,2-3=
(4) 一般地,为了使同底数幂的除法 am÷an=am-n (m,n是正整数,m≥n,a≠0) 当m<n 时也成立,你认为应对负整数指数幂的意义做怎样的规定
我们规定,
a-p = (a≠0,p是正整数).
这就是说,任何不等于零的数的- p(p为正整数)次幂,等于这个数的p次幂的倒数.
零的负整数指数幂没有意义.
(5) 想一想,在上面的规定中,为什么有a 的限制
例 3
计算:4-3,(-1)-3,(0.2) -2.
例 4
练 习
1. 以下是法定长度计量单位对照和换算表:
(1)用小数表示,1毫米、1微米、1纳米各是多少米
1毫米= 0.001米,
1微米= 0.000001米,
1纳米= 0.000000001米。
(2)用正整数指数幂表示 ,1厘米等于多少纳米 多少飞米
1厘米=107纳米,
1厘米 =1012飞米。
(3) 用负整数指数暴表示,1飞米等于多少纳米 多少微米 多少厘米
1飞米=10-6纳米=10-9微米=10-13厘米。
2.计算:5-2,10-4,(-3)-3,()-4.
交流与发现
引入了零指数和负整数指数之后,正整数指数幂的运算性质能继续使用吗
(1) 观察下面两组含有零指数幂和负整数指数幂的算式:
分别按照整数指数幂的意义和仿照同底数幂的乘法与除法的运算性质进行计算,所得到的结果是否相同
对于同一个算式,这两种算法的结果是相同的.
由此可见,同底数幂乘法和除法的运算性质在整数范围内仍能使用.
(2) 你能通过举例,验证积的乘方和幂的乘方的运算性质对于零指数和负整数指数仍能使用吗 与同学交流.
(3) 由上面的验证过程,你能得到什么结论
引人零指数和负整数指数后,原有的正整数指数幂的运算性质可以扩展到全体整数指数.
例 5
计算:(1) 52÷5-1;
例 6
计算:(1) x5·x-3;
(2) (-a2b)÷(-a2b)-2.
练 习
1. 计算:
=
=
=
=
=
=
交流与发现
江河湖海都是由一滴滴水汇集而成,每一滴水中含有许许多多的水分子.
小资料
一滴水的体积大约为 0.05 毫升,质量大约为0.05克,含有大约1 670 000 000 000 000 000 000=1.67×1021 个水分子.
一滴水
一个水分子的质量大约为 0.000 000 000 000 000 000 000 3 克,这样小的数写起来太麻烦了,有没有其他的记法呢
如果能像记一个大数那样用科学记数法表示就好了.
根据乘方的意义,填写下表:
0.001
3
0.0001
4
你发现10的负整数指数幂用小数表示时有什么规律吗
10-n = 0.00 ··· 01.
n个0
利用10的负整数指数幂,一个水分子的质量可写成
0.000 000 000 000 000 000 000 03
=3×0.00 ··· 01
23个0
=3×10-23(克)
同样地,一个水分子的半径为0.000 000 001 925米,可写成1.925×10-9米.
一个绝对值小于1的非零小数可以记作±a×10-n的形式,其中1≤a<10,n是正整数.
这种记数方法,是绝对值小于1的非零小数的科学记数法
在上面的科学记数法中,n 等于原数中第一个非零数字前面所有零的个数 (包括小数点前面的那个零).
例如,0.000 012 3 =1.23×10-5,
-0.35=-3.5×10-1
写成科学记数法形式±a×10-n的数,可以在计算器上表示.
见课本102页
例 7
安哥拉长毛兔最细的兔毛直径约为5×10-6米,将这个数写成小数的形式.
5×10-6 = 0.000 005.
所以,安哥拉长毛兔最细的兔毛直径约为0.000 005米.
例 8
已知某花粉直径为360 000纳米,用科学记数法表示,该花粉的直径是多少米
1纳米= 10米,
360 000×10-9= 3.6×10-4
该花粉的直径为3.6×10-4米
练 习
1.用科学记数法表示下列各数,并用计算器进行验证:
(1) 0.000 08;
(2) 0.000 000 100 2;
(3) 0.300 1;
(4) -0.000 408.
8×10-5
1.002×10-7
3.001×10-1
-4.08×10-4
2. 先将2.385×10-8输入计算器,再写成小数的形式.
2.385×10-8=0.000 000 023 85
3. 解答本章“情境导航”中的问题(精确到1019个).
当你站在海边,眺望一望无际的大海时,可曾想到世界海洋的容积有多大 海水是由一个个水分子组成的,一个水分子的质量是3×10-23克,在1滴水中大约有多少个水分子
略
习题 11.6
复习与巩固
1. 计算:50,(-1)0,(a-b)0.
50 = 1,
(-1)0= 1,
(a-b)0= 1
2. 计算:20-2,5-3,8-4,(a-b)-2.
3. 计算:
(1) b2÷b3 · b8;
(2) 108×100×10-2;
(3) (m3·m5) ÷(m·m9);
(4) q6÷q3÷q5;
(5) 3-2×33;
(7) (x-5)2;
(6) a3÷a-5;
(8) (t3y) -2.
4. 用负整数指数幂表示:
(1) 1平方厘米等于多少平方米 多少平方千米
(2) 1立方厘米等于多少立方米 多少立方千米
1平方厘米=10-4平方米=10-7平方千米
1立方厘米=10-6立方米=10-9立方千米
5. 光在真空中的传播速度约为 300 000千米/秒,那么光
每前进1米用多少时间(精确到10-10秒)
光在真空中的传播速度约为:
300000千米/秒= 3 × 108米/秒,
则光每前进1米所用时间为 = 3.3×10-9秒
6. 蓝鲸是地球上最重的动物,成年蓝鲸的质量可达 150吨,而一条沙丁鱼的质量约为 30克.一条蓝鲸的质量是一条沙丁鱼质量的多少倍
反之,一条沙丁鱼的质量是一
条蓝鲸质量的多少倍
因为成年蓝鲸的质量可达150吨= 1.5×108克,一条沙丁鱼的质量约为30克,
7. 用科学记数法表示下列各数:
0.085;
(2) - 0.000 085.
=8.5 ×10-2
=8.5 ×10-5
8. 将下列各数写成小数的形式:
(1) 3.67×10-5;
(2) -2.8 ×10-6.
0.000 0367
-0.0000028
9. 在计算器上分别输入下列各数:
(1) 2.818 2×10-5;
(2) 1.6×10-8.
略
10. 计算 ( 结果用科学记数法表示 ):
( 8.616 2×10-3) × 10-8;
(2) ( 6.12×10-8 ) ÷(-1.2 ×10-5 ).
8.6162 ×10-11
-5.1×10-3
11. 填空(在方框内填上合适的数 ):
1.618 ×10 = 0.000 161 8;
(2) ×10 = 0.000 818 2.
-4
8.182
-4
拓展与延伸
12. 计算:
(1) (y-x)3÷ (y-x)-2;
(2) (-2)100 ÷ (-2)-101;
(3) ()-2× ()-3;
(4) (a-2b-3)-3.
13. 填空 (在方框内填上合适的数 ):
(1) x ÷ x5= x-2;
(2) m5 ÷ m2 · m = m-2.
3
-5
14. 1毫秒等于10-3秒,那么1毫秒等于多少小时 (用科学
记数法表示,精确到10时)
15. 太阳释放的辐射能功率为 3.8×1023 千瓦,到达地球的仅占20亿分之一.到达地球的辐
射能功率是多少千瓦 (用科学记数法
表示,精确到1013千瓦)
探索与创新
16. 人们用“捡了芝麻,丢了西瓜”比喻因小失大.有人做过实验,2万粒芝麻的质量
约 80 克,如果一个西瓜的质量
为4千克,一粒芝麻的质量是这
个西瓜的质量的多少倍
17. 请查阅资料,举出几个用科学记数法表示绝对值小于1的非零小数的实际数据,并编制一道数学应用题.
略
本课结束!
第11章 整式的乘除
青岛版 七年级下册
11 . 6
零指数幂与负整数指数幂
复习提问
回忆正整数指数幂的运算性质:
(m,n是正整数);
(2) 幂的乘方:
(m,n是正整数);
(1) 同底数的幂的乘法:
(3) 积的乘方:
(n是正整数);
(4) 同底数的幂的除法:
( a≠0,m,n是正整数,m>n);
(5) 商的乘方:
(n是正整数);
2、am÷an=am-n ( a≠0,m,n是正整数,m>n);
在同底数幂的除法公式时,有一个附加条件:m>n,即被除数的指数大于除数的指数.
当被除数的指数不大于除数的指数,即m=n或m<n时,情况怎样呢?
观察与思考
(1) 你听说过这样一个故事吗 古印度舍罕国王打算重赏国际象棋发明者宰相西萨. 西萨要求在棋盘的第1个格内只赏 1粒麦子,在第 2个格内只赏2粒,第3 个格内只赏4粒,
以后的每格内都比上一格的麦粒多放1倍,直至第 64格——棋盘的最后 1格.结果国王找人一算,发现即使把国库中的全部麦子都给这位宰相,还远远不够!
在这个故事中,从第2个格开始,各方格的麦粒数都可以写成底数是2的正整数指数幂的形式,如下表所示:
方格序号 1 2 3 4 5 ··· 64
麦粒个数 1 21 22 23 24 ··· 263
能把第1个格内的麦粒数也写成底数为2的幂的形式吗
方格序号 1 2 3 4 5 ··· 64
麦粒个数 1 21 22 23 24 ··· 263
按照表中的规律,第1个格中的麦粒数用底数是2的幂表示,应写成 20,不过,这样就出现零指数了.
“20=1”,这在数学上合理吗
(2) 观察除式 23÷23,你发现被除式和除式有哪些特点 如何计算它们的商?
由于被除数和除数相等,因此它们的商等于1,即
23÷23= 1.
为了使被除式的指数等于除式的指数时,同底数幂除法的运算性质也能使用,应当规定20=1.
如果仿照同底数幂除法的运算性质进行计算,就得:
23÷23=23-3=20.
(3) 一般地,为了使同底数幂的除法性质 am÷an=
am-n (m,n 是正整数,m>n,a≠0) 当m=n 时也成立,你认为应对零指数幂的意义作怎样的规定
a0=1 (其中a≠0)
这就是说,
任何不等于零的数的零次幂等于1,
零的零次幂没有意义.
这样一来,幂指数的范围从正整数扩充到全体自然数了.
例如,100=1,(-)0 = 1.你能再举出几个数的零次幂的例子吗
(4) 在上面的规定中,为什么有a≠0的限制 与同学交流.
例 1
计算:2x0 (x=0).
2x0=2× 1 = 2.
例 2
计算:a2÷a0·a2 (a≠0).
a2÷a0 · a2=a2÷l · a2=a2 · a2=a4
想一想,a2÷ (a0 · a2)等于什么
练 习
1. 计算:
(1) 60 ; (2) (-8)0;
(3) (x-y)0(x≠y); (4) ×(-)0
=1
=1
=1
=
(5) ( 100×20) ÷(10 ×20); (6) 103÷100× 105.
=(100×1)2 ÷ (10×1)2
= 100 ÷ 10
= 10
=103-0+5
= 108
2. 填空(在方框内填上合适的数 ):
(1) a2÷a =a ( a ≠ 0);
(2) x · x2 · x = x5 · x0 ( x ≠ 0 ).
0
3
3. 当a为怎样的有理数时,(a - 1)0 = 1
观察与思考
(1) 如图,数轴上点A表示的数是8,一动点P从点A出发,向左按以下规律跳动:第1次跳动到OA的中点A1处,第2次从A1点跳动到OA1的中点A2,处,第3次从A2点跳动到 OA2,的中点A3处.
如果把点A表示的数写成23,那么点A1,A2,A3应怎样分别用底数是2的幂的形式表示
点 A,A1,A2,A3依次可以写成23,22,21,20,
这里23=8,22=4,21=2,20=1.
(2) 如果动点P按(1)中的规律继续向左跳动到点 A4,A5,A6,···处,你能把点 A4,A5,A6 所表示的数写成2的整数指数幂的形式吗 它们应当分别等于多少
按照上面的规律,点A4,A5,A6 所表示的数写成底数是2的幂的形式,应分别是 2-1,2-2,2-3. 不过,这样就出现负整数指数幂了.
按照上面的规律,点A4,A5,A6 所表示的数分别是,,· 应当有2-1 = ,2-2= ,2-3= . 这在数学上合理吗
(3) 观察除式22÷23 和22÷24.你发现被除式和除式有哪些特点 如何计算它们的商
由分数的意义和约分法则,得:
如果仿照同底数幂除法的运算性质进行计算,就得
22÷23=22-3 = 2-1;
22÷24=22-4=2-2
为了使被除式的指数小于除式的指数时,同底数幂除法的运算性质也能使用,应当规定
2-1 = ,2-2= ,2-3=
(4) 一般地,为了使同底数幂的除法 am÷an=am-n (m,n是正整数,m≥n,a≠0) 当m<n 时也成立,你认为应对负整数指数幂的意义做怎样的规定
我们规定,
a-p = (a≠0,p是正整数).
这就是说,任何不等于零的数的- p(p为正整数)次幂,等于这个数的p次幂的倒数.
零的负整数指数幂没有意义.
(5) 想一想,在上面的规定中,为什么有a 的限制
例 3
计算:4-3,(-1)-3,(0.2) -2.
例 4
练 习
1. 以下是法定长度计量单位对照和换算表:
(1)用小数表示,1毫米、1微米、1纳米各是多少米
1毫米= 0.001米,
1微米= 0.000001米,
1纳米= 0.000000001米。
(2)用正整数指数幂表示 ,1厘米等于多少纳米 多少飞米
1厘米=107纳米,
1厘米 =1012飞米。
(3) 用负整数指数暴表示,1飞米等于多少纳米 多少微米 多少厘米
1飞米=10-6纳米=10-9微米=10-13厘米。
2.计算:5-2,10-4,(-3)-3,()-4.
交流与发现
引入了零指数和负整数指数之后,正整数指数幂的运算性质能继续使用吗
(1) 观察下面两组含有零指数幂和负整数指数幂的算式:
分别按照整数指数幂的意义和仿照同底数幂的乘法与除法的运算性质进行计算,所得到的结果是否相同
对于同一个算式,这两种算法的结果是相同的.
由此可见,同底数幂乘法和除法的运算性质在整数范围内仍能使用.
(2) 你能通过举例,验证积的乘方和幂的乘方的运算性质对于零指数和负整数指数仍能使用吗 与同学交流.
(3) 由上面的验证过程,你能得到什么结论
引人零指数和负整数指数后,原有的正整数指数幂的运算性质可以扩展到全体整数指数.
例 5
计算:(1) 52÷5-1;
例 6
计算:(1) x5·x-3;
(2) (-a2b)÷(-a2b)-2.
练 习
1. 计算:
=
=
=
=
=
=
交流与发现
江河湖海都是由一滴滴水汇集而成,每一滴水中含有许许多多的水分子.
小资料
一滴水的体积大约为 0.05 毫升,质量大约为0.05克,含有大约1 670 000 000 000 000 000 000=1.67×1021 个水分子.
一滴水
一个水分子的质量大约为 0.000 000 000 000 000 000 000 3 克,这样小的数写起来太麻烦了,有没有其他的记法呢
如果能像记一个大数那样用科学记数法表示就好了.
根据乘方的意义,填写下表:
0.001
3
0.0001
4
你发现10的负整数指数幂用小数表示时有什么规律吗
10-n = 0.00 ··· 01.
n个0
利用10的负整数指数幂,一个水分子的质量可写成
0.000 000 000 000 000 000 000 03
=3×0.00 ··· 01
23个0
=3×10-23(克)
同样地,一个水分子的半径为0.000 000 001 925米,可写成1.925×10-9米.
一个绝对值小于1的非零小数可以记作±a×10-n的形式,其中1≤a<10,n是正整数.
这种记数方法,是绝对值小于1的非零小数的科学记数法
在上面的科学记数法中,n 等于原数中第一个非零数字前面所有零的个数 (包括小数点前面的那个零).
例如,0.000 012 3 =1.23×10-5,
-0.35=-3.5×10-1
写成科学记数法形式±a×10-n的数,可以在计算器上表示.
见课本102页
例 7
安哥拉长毛兔最细的兔毛直径约为5×10-6米,将这个数写成小数的形式.
5×10-6 = 0.000 005.
所以,安哥拉长毛兔最细的兔毛直径约为0.000 005米.
例 8
已知某花粉直径为360 000纳米,用科学记数法表示,该花粉的直径是多少米
1纳米= 10米,
360 000×10-9= 3.6×10-4
该花粉的直径为3.6×10-4米
练 习
1.用科学记数法表示下列各数,并用计算器进行验证:
(1) 0.000 08;
(2) 0.000 000 100 2;
(3) 0.300 1;
(4) -0.000 408.
8×10-5
1.002×10-7
3.001×10-1
-4.08×10-4
2. 先将2.385×10-8输入计算器,再写成小数的形式.
2.385×10-8=0.000 000 023 85
3. 解答本章“情境导航”中的问题(精确到1019个).
当你站在海边,眺望一望无际的大海时,可曾想到世界海洋的容积有多大 海水是由一个个水分子组成的,一个水分子的质量是3×10-23克,在1滴水中大约有多少个水分子
略
习题 11.6
复习与巩固
1. 计算:50,(-1)0,(a-b)0.
50 = 1,
(-1)0= 1,
(a-b)0= 1
2. 计算:20-2,5-3,8-4,(a-b)-2.
3. 计算:
(1) b2÷b3 · b8;
(2) 108×100×10-2;
(3) (m3·m5) ÷(m·m9);
(4) q6÷q3÷q5;
(5) 3-2×33;
(7) (x-5)2;
(6) a3÷a-5;
(8) (t3y) -2.
4. 用负整数指数幂表示:
(1) 1平方厘米等于多少平方米 多少平方千米
(2) 1立方厘米等于多少立方米 多少立方千米
1平方厘米=10-4平方米=10-7平方千米
1立方厘米=10-6立方米=10-9立方千米
5. 光在真空中的传播速度约为 300 000千米/秒,那么光
每前进1米用多少时间(精确到10-10秒)
光在真空中的传播速度约为:
300000千米/秒= 3 × 108米/秒,
则光每前进1米所用时间为 = 3.3×10-9秒
6. 蓝鲸是地球上最重的动物,成年蓝鲸的质量可达 150吨,而一条沙丁鱼的质量约为 30克.一条蓝鲸的质量是一条沙丁鱼质量的多少倍
反之,一条沙丁鱼的质量是一
条蓝鲸质量的多少倍
因为成年蓝鲸的质量可达150吨= 1.5×108克,一条沙丁鱼的质量约为30克,
7. 用科学记数法表示下列各数:
0.085;
(2) - 0.000 085.
=8.5 ×10-2
=8.5 ×10-5
8. 将下列各数写成小数的形式:
(1) 3.67×10-5;
(2) -2.8 ×10-6.
0.000 0367
-0.0000028
9. 在计算器上分别输入下列各数:
(1) 2.818 2×10-5;
(2) 1.6×10-8.
略
10. 计算 ( 结果用科学记数法表示 ):
( 8.616 2×10-3) × 10-8;
(2) ( 6.12×10-8 ) ÷(-1.2 ×10-5 ).
8.6162 ×10-11
-5.1×10-3
11. 填空(在方框内填上合适的数 ):
1.618 ×10 = 0.000 161 8;
(2) ×10 = 0.000 818 2.
-4
8.182
-4
拓展与延伸
12. 计算:
(1) (y-x)3÷ (y-x)-2;
(2) (-2)100 ÷ (-2)-101;
(3) ()-2× ()-3;
(4) (a-2b-3)-3.
13. 填空 (在方框内填上合适的数 ):
(1) x ÷ x5= x-2;
(2) m5 ÷ m2 · m = m-2.
3
-5
14. 1毫秒等于10-3秒,那么1毫秒等于多少小时 (用科学
记数法表示,精确到10时)
15. 太阳释放的辐射能功率为 3.8×1023 千瓦,到达地球的仅占20亿分之一.到达地球的辐
射能功率是多少千瓦 (用科学记数法
表示,精确到1013千瓦)
探索与创新
16. 人们用“捡了芝麻,丢了西瓜”比喻因小失大.有人做过实验,2万粒芝麻的质量
约 80 克,如果一个西瓜的质量
为4千克,一粒芝麻的质量是这
个西瓜的质量的多少倍
17. 请查阅资料,举出几个用科学记数法表示绝对值小于1的非零小数的实际数据,并编制一道数学应用题.
略
本课结束!
同课章节目录
- 第8章 角
- 8.1 角的表示
- 8.2 角的比较
- 8.3 角的度量
- 8.4 对顶角
- 8.5 垂直
- 第9章 平行线
- 9.1 同位角、内错角、同旁内角
- 9.2 平行线和它的画法
- 9.3 平行线的性质
- 9.4 平行线的判定
- 第10章 一次方程组
- 10.1 认识二元一次方程组
- 10.2 二元一次方程组的解法
- 10.3 三元一次方程组
- 10.4 列方程组解应用题
- 第11章 整式的乘除
- 11.1 同底数幂的乘法
- 11.2 积的乘方与幂的乘方
- 11.3 单项式的乘法
- 11.4 多项式乘多项式
- 11.5 同底数幂的除法
- 11.6 零指数幂与负整数指数幂
- 第12章 乘法公式与因式分解
- 12.1 平方差公式
- 12.2 完全平方公式
- 12.3 用提公因式法进行因式分解
- 12.4 用公式法进行因式分解
- 第13章 平面图形的认识
- 13.1 三角形
- 13.2 多边形
- 13.3 圆
- 第14章 位置与坐标
- 14.1 用有序数对表示位置
- 14.2 平面直角坐标系
- 14.3 直角坐标系中的图形
- 14.4 用方向和距离描述两个物体的相对位置
